Метод конечных разностей или метод сеток
СОДЕРЖАНИЕ: Рассмотрим линейную краевую задачу (2.24) (2.25) непрерывны на [a, b]. Разобьем отрезок [a, b] на n равных частей длины, или шага Точки разбиения называются узлами, а их совокупность – сеткой на отрезке [a, b]. Значения в узлах искомой функцииМетод конечных разностей, или метод сеток
Рассмотрим линейную краевую задачу
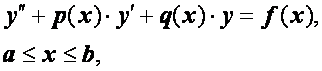(2.24)
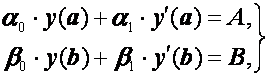(2.25)
,
где 
,
,и
непрерывны на [a
,b
].
Разобьемотрезок [a , b ]на n равных частей длины, или шага
.
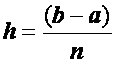Точки разбиения
, 
называютсяузлами
, а их совокупность – сеткой
на отрезке [a
,b
]. Значения в узлах искомой функции 
и ее производных
обозначим соответственно через
.
Введем обозначения
Заменим производные так называемыми односторонними конечно-разностными отношениями :
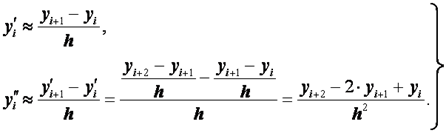(2.26)
Формулы (2.26) приближенно выражают значения производных во внутренних точках интервала[ a , b ] .
Для граничных точек положим
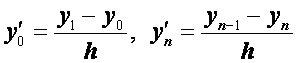. (2.27)
Используя формулы (2.26), дифференциальное уравнение (2.24) при 
, (i
=
1, 2,..., n
–1) приближенно можно заменить линейной системой уравнений
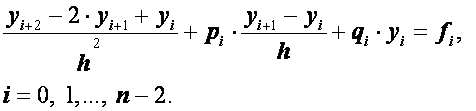(2.28)
Кроме того, в силу формул(2.27) краевые условия (2.25) дополнительно дают еще два уравнения:
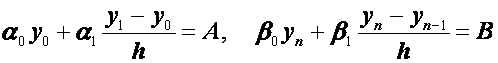. (2.29)
Таким образом, получена линейная системаn
+
1уравнений сn
+
1неизвестными 
, представляющими собой значения искомой функции 
в узлах сетки. Система уравнений (2.28), (2.29), заменяющая приближенно дифференциальную краевую задачу(2.24), (2.25)обычно называется разностной схемой
. Решить эту систему можно каким-либо общим численным методом. Однако схема (2.28), (2.29) имеет специфический вид и ее можно эффективно решить специальным методом, называемым методом прогонки. Специфичность системы заключается в том, что уравнения ее содержат три соседних неизвестных и матрица этой системы является трехдиагональной.
Преобразуем уравнения (2.28):
. (2.30)
Введя обозначения
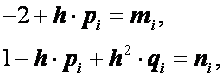
получим
, (i
=0, 1,..., n
-2).(2.31)
Краевые условия по-прежнему запишем в виде
. (2.32)
Метод прогонки состоит в следующем.
Разрешим уравнение (2.31) относительно 
:
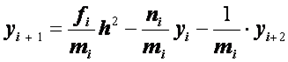. (2.33)
Предположим, что с помощью полной системы (2.31) из уравнения исключен член, содержащий
. Тогда уравнение (2.33) может быть записано в виде
, (2.34)
где
и
должны быть определены. Найдем формулы для этих коэффициентов. При i
=
0 из формулы (2.33) и краевых условий (2.32) следует, что
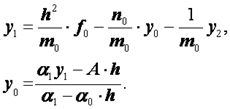
Исключая из этих двух уравнений 
, найдем
.
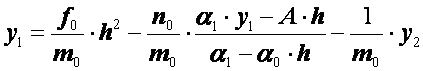Выразим теперь отсюда 
:
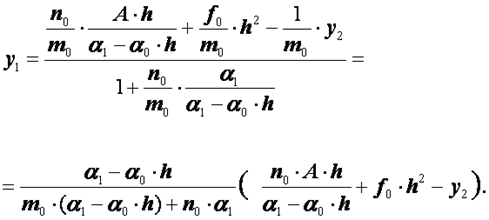(2.35)
Но, согласно формуле (2.34),
(2.36)
Сравнивая теперь (2.35) и (2.36), найдем, что
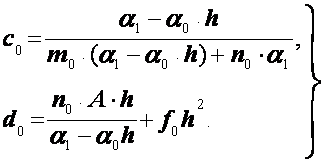(2.37)
Пусть теперьi
0, то есть i
=
1, 2,..., n
–
2. Выражая 
по формуле (2.34), получим:
.
Подставляя это в формулу (2.33), будем иметь
.
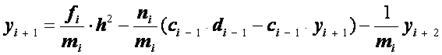Разрешая полученное уравнение относительно
, находим
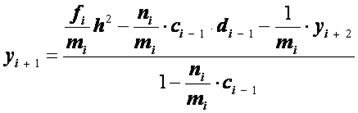, или
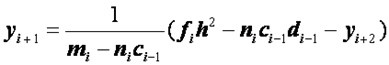. (2.38)
Отсюда, сравнивая формулы (2.34) и (2.38), получаем для коэффициентов
и
рекуррентные формулы:
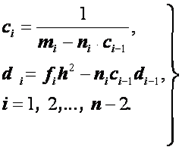(2.39)
Так как
и
уже определены по формулам (2.37), то, используя формулы (2.39), можно последовательно определить коэффициенты
и
до
и
включительно. Эти вычисления называются прямым ходом
метода прогонки.
Из формулы (2.33) при i = n – 2 и второго краевого условия (2.32) получаем
Разрешая эту систему относительно
, будем иметь
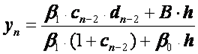. (2.40)
Теперь, используя (2.34) и первое краевое условие (2.32), мы можем последовательно найти 
. Это обратный ход
метода прогонки.
Итак, получаем следующую цепочку:
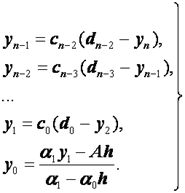(2.41)
Для простейших краевых условий 
формулы для
и
упрощаются. Полагая в этом случае 
из формул (2.37), (2.40), (2.41) будем иметь
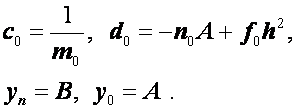
Рассмотренный нами подход сводит линейную краевую задачу к системе линейных алгебраических уравнений. При этом возникает три вопроса.
1)Существует ли решение алгебраической системы типа (2.31)?
2)Как фактически находить это решение?
3)Сходится ли разностное решение к точному при стремлении шага сетки к 0?
Можно доказать, что если краевая задача имеет вид
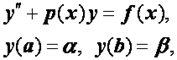
причем р ( x ) 0, то решение системы (2.31), (2.32) существует и единственно. Фактическое отыскание решения можно провести, например, методом прогонки. На третий вопрос дает ответследующая
Теорема
Если
и
дважды непрерывно дифференцируемы, то разностное решение, соответствующее схеме с заменой
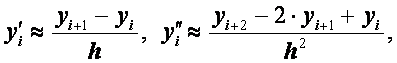
равномерно сходится к точному с погрешностью
при
Таким образом, схема (2.28), (2.29) дает приближенное решение краевой задачи, но точность ее весьма мала. Это связано с тем, что аппроксимация производной
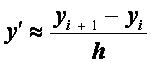
имеет низкий порядок точности погрешность этой аппроксимации
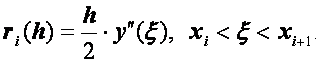
Более точную разностную схему можно получить, если при переходе от линейной краевой задачи к конечно-разностным уравнениям воспользоваться центральными формулами для производных:
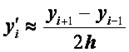, (2.42)
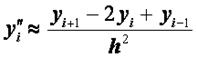, (2.43)
i = 1, 2,...,n .
Погрешность формулы (2.42) выражается так:
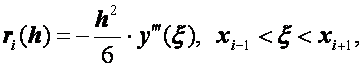
то есть формула (2.42) имеет второй порядок точности относительно шага сетки h . Подставляя выражения (2.42), (2.43) в задачу (2.24), (2.25) и выполняя некоторые преобразования, получим следующую систему:
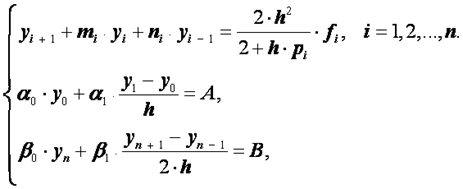(2.44)
Где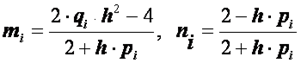
.
Система (2.44) снова трехдиагональная и ее решение также можно получить методом прогонки. Его алгоритм здесь будет выглядеть так. Сначала находят коэффициенты
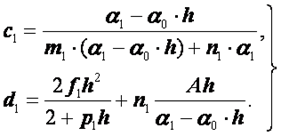(2.45)
Затем определяют коэффициенты 
по следующим рекуррентным формулам:
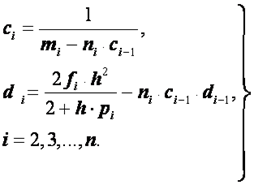(2.46)
Обратный ход начинается с нахождения
:
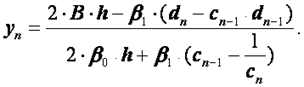(2.47)
После этого находим 
по формулам:
, (2.48)
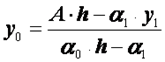. (2.49)
Относительно схемы (2.44) можно также доказать, что она имеет единственное решение пр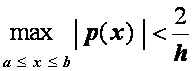и
и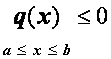
,
и это решение может быть найдено описанным методом прогонки. Кроме того, для схемы (2.44) имеет место
Теорема
Пусть решение граничной задачи (2.24), (2.25) единственно и непрерывно дифференцируемо на [a , b ] до четвертого порядка точности включительно. Если выполняются условия
,
,
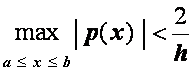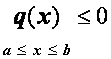то схема
(2.44)будет равномерно сходиться к решению задачи
(2.24), (2.25)с погрешностью
.
Заметим, что условия, приводимые в теоремах, являются достаточными, а отнюдь не необходимыми. Поэтому в практике численных расчетов нарушение этих условий обычно не вызывает заметного ухудшения расчетных схем.