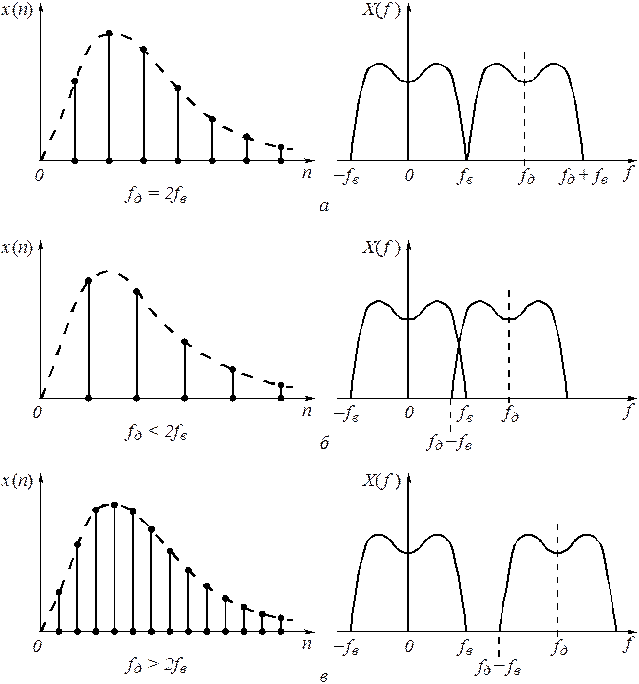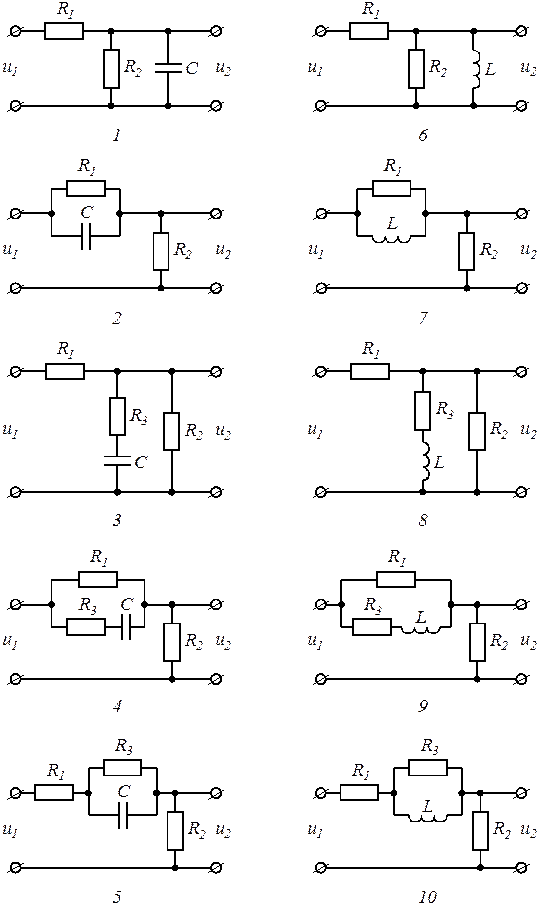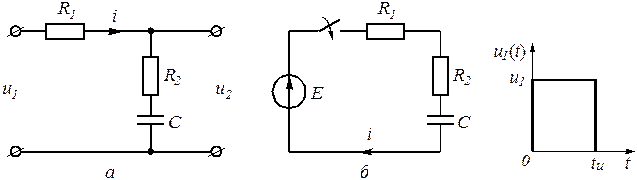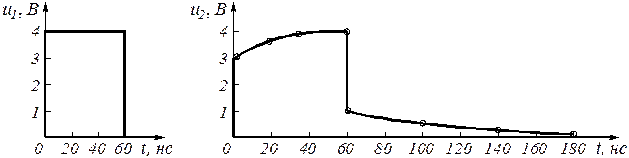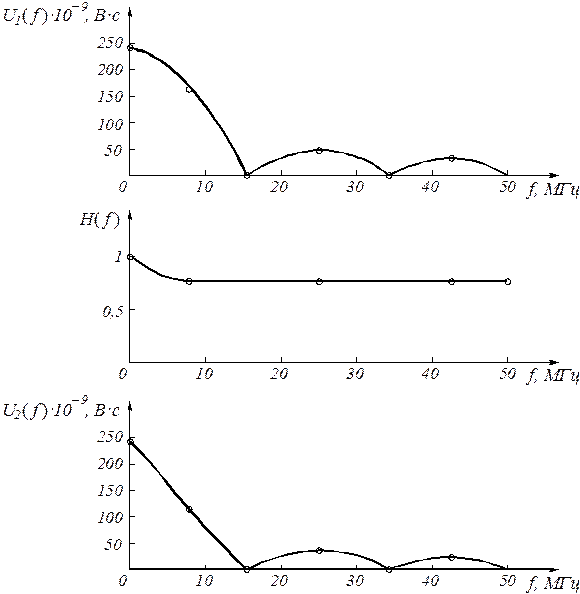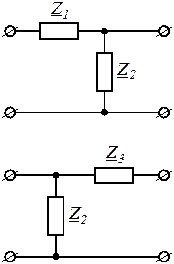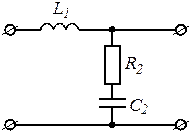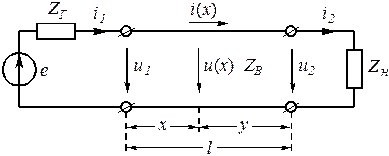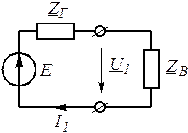Методические указания и контрольные задания №3 и №4 по курсу теория электрических цепей для студентов заочного факультета 3 курса
СОДЕРЖАНИЕ: Д. т н., профессор В. П. Бакалов, к т н., доцент В. М. Рожков. Методические указания и контрольные задания №3 и №4 по курсу теория электрических цепей для студентов заочного факультета 3 курсаГосударственный комитет РФ по связи и информатизации
Сибирский государственный университет телекоммуникаций
и информатики
В.П. Бакалов, В.М. Рожков
Методические указания
и контрольные задания № 3 и № 4
по курсу
ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
для студентов заочного факультета
3 курса
Новосибирск 1999
УДК 621.3.01
Д.т.н., профессор В.П. Бакалов, к.т.н., доцент В.М. Рожков. Методические указания и контрольные задания № 3 и № 4 по курсу теория электрических цепей для студентов заочного факультета 3 курса.
Рассматриваются разделы курса ТЭЦ, изучаемые на 3 курсе заочного факультета (5 и 6 семестры). Приводятся контрольные задания, составленные по стовариантной системе. Даны решения типовых задач.
Кафедра ТЭЦ.
Ил. 18, табл. 8.
Рецензент
Для специальностей 200900, 201000, 201100, 201200.
Утверждено редакционно-издательским советом СибГУТИ в качестве методических указаний.
© Сибирский государственный университет телекоммуникаций и информатики
ОБЩИЕ ЗАМЕЧАНИЯ
Методические указания посвящены разделам курса ТЭЦ, которые изучаются студентами заочного факультета на 3 курсе в 5-ом и 6-ом семестрах.
Для самостоятельной работы студенту достаточно иметь учебник [1] и задачник [2]. В отсутствие указанной литературы могут быть рекомендованы учебники [3 6], задачник [7] и учебное пособие [8]. Особое внимание следует обратить на приобретение навыков решения задач. Примеры на решения типовых задач приведены в [2, 7] и в настоящих методических указаниях.
Домашние контрольные работы, проверенные и исправленные согласно всем замечаниям рецензента, предъявляются на зачете или экзамене. Студент должен быть готов дать пояснения по решению каждой задачи в контрольной работе и по исправлениям ошибок, указанных рецензентом.
Для помощи в самостоятельной работе кафедра ТЭЦ организует индивидуальные консультации (по расписанию). Иногородние студенты могут получить письменную консультацию, направив свои вопросы письмом на кафедру.
Для вызова на зимнюю лабораторно-экзаменационную сессию студент должен выполнить контрольную работу № 3, для вызова на весеннюю сессию должен выполнить контрольную работу № 4 и курсовую работу. Контрольные и курсовая работы должны быть высланы по почте или переданы лично на проверку в центр обработки контрольных работ университета не позже, чем за четыре недели до начала соответствующей лабораторно-экзаменационной сессии.
На зимней сессии студент (по расписанию своей группы) прослушивает по ТЭЦ 10 двухчасовых лекций, посещает 4 двухчасовых упражнения, выполняет 4 двухчасовые лабораторные работы. В конце сессии студент сдает зачет по ТЭЦ. Билеты на зачете содержат одну задачу и один теоретический вопрос.
На весенней сессии по ТЭЦ полагается 7 двухчасовых лекций, 6 двухчасовых лабораторных занятий. Завершается сессия по ТЭЦ защитой курсовой работы и экзаменом. Билеты на экзамене содержат одну задачу и два теоретических вопроса.
Вопросы и задачи в билетах на экзамене и на зачете приближены к вопросам, перечисленным ниже в методических указаниях по изучаемым темам и к вопросам для самоконтроля.
Список литературы
1. Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических цепей. М.: Радио и связь. 1998.
2. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. Учебное пособие для вузов. 4-е изд., перераб. и доп. М.: «Высшая школа». 1990.
3. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических цепей и электроники. М.: Радио и связь. 1989.
4. Андреев Б.С. Теория нелинейных электрических цепей. М.: Радио и связь. 1982.
5. Белецкий А.Ф. Теория линейных электрических цепей. М.: Радио и связь. 1986.
6. Гоноровский И.С. Радиотехнические цепи и сигналы. 4-е изд., перераб. и доп. М.: Радио и связь. 1986.
7. Воробиенко П.П. Теория линейных электрических цепей. Сб. задач и упражнений. М.: Радио и связь. 1989.
8. Бакалов В.П., Журавлева О.Б., Крук Б.И. Теория электрических цепей. Учебное пособие для дистанционного обучения. Новосибирск: Из-во СИБГАТИ. 1998.
Методические указания к разделам курса,
изучаемым в пятом семестре
Переходные процессы в линейных
электрических цепях. Классический
метод анализа
[1. Гл. 6]; [2. Гл. 8]; [3. §§ 7.1 – 7.6]; [5. Гл. 4, Гл. 8]; [7. Гл. 8]; [8. стр. 112 – 133].
Изучаемые вопросы
1. Переходный режим электрических цепей. Законы коммутации.
2. Классический метод расчета переходных процессов.
3. Переходные процессы в цепях первого порядка.
4. Переходные процессы в цепях второго порядка.
5. Включение RLC -контура на постоянное и гармоническое напряжение.
6. Переходные процессы в разветвленных цепях.
Пояснения к изучаемым вопросам
1. Обратить внимание на то, что в ходе переходного процесса в электрических цепях обязательно происходит изменение энергии электрического поля в емкостных элементах цепей (изменение напряжения на емкости) и изменение энергии магнитного поля в индуктивных элементах (изменение тока в индуктивности).
2. Функция, описывающая ток или напряжение в цепи во время переходного процесса, в общем случае имеет вид:
![]() ,
,
где ![]() – принужденная (установившаяся) составляющая, а
– принужденная (установившаяся) составляющая, а ![]() – свободная составляющая переходного процесса. Принужденная составляющая определяет ток или напряжение в цепи после окончания переходного процесса, т.е. их значение в установившемся (стационарном) состоянии после коммутации. В цепях постоянного тока это постоянная величина, в цепях гармонического тока это функция времени. Рассчитывается
– свободная составляющая переходного процесса. Принужденная составляющая определяет ток или напряжение в цепи после окончания переходного процесса, т.е. их значение в установившемся (стационарном) состоянии после коммутации. В цепях постоянного тока это постоянная величина, в цепях гармонического тока это функция времени. Рассчитывается ![]() при t
= .
при t
= .
Полезно иметь ввиду, что в цепях постоянного тока ток через емкость при ![]() и t
= всегда равен нулю и что напряжение на индуктивности при
и t
= всегда равен нулю и что напряжение на индуктивности при ![]() и t
= тоже всегда равно нулю.
и t
= тоже всегда равно нулю.
3. Обратить внимание на физический смысл постоянных времени неразветвленных цепей RL
и RC
: ![]() и
и ![]() .
.
В цепи
RL
. Чем больше L
, тем больше может измениться энергия магнитного поля ![]() , тем дольше будет протекать процесс изменения ее. Чем больше R
, тем меньше изменение тока
, тем дольше будет протекать процесс изменения ее. Чем больше R
, тем меньше изменение тока ![]() , тем меньше изменение
, тем меньше изменение ![]() , тем быстрее переходный процесс.
, тем быстрее переходный процесс.
В цепи
RC
. Чем больше C
, тем больше энергия электрического поля ![]() , тем дольше она будет изменяться. Чем больше R
, тем меньше изменение тока в цепи, тем медленнее изменение напряжения на емкости.
, тем дольше она будет изменяться. Чем больше R
, тем меньше изменение тока в цепи, тем медленнее изменение напряжения на емкости.
Теоретически переходный процесс заканчивается при t = . Практически длительность переходного процесса связывают с требуемой точностью расчета. Например, если допустимая погрешность расчетов составляет 5%, то длительность переходного процесса определяется временем 3t от момента возникновения процесса.
4. Основные особенности анализа рассматриваются на примере, описывающем разряд емкости на цепь RL . Обратить внимание на то, что переходный процесс в этом случае может иметь апериодический, колебательный или критический характер. Необходимо уметь объяснить временные диаграммы процесса для каждого случая.
При апериодическом разряде свободная составляющая процесса определяется суммой двух экспонент. Тогда длительность разряда будет определяться экспонентой, имеющей бльшую постоянную времени.
При колебательном характере кривые тока разряда и напряжений на L
и на С
расположены «внутри» огибающих экспонент, которые определяются функцией вида exp(–a
t
). Длительность переходного процесса зависит от постоянной времени этих экспонент, равной ![]() .
.
При критическом характере кривые процесса аналогичны кривым при апериодическом разряде, но имеют меньшую длительность.
5. Обратить внимание на временные диаграммы изменения токов и напряжений.
6. Разобрать решения задач в [1. §. 6.6], в [2. № 8.26].
Операторный метод анализа переходных
процессов в линейных цепях
[1. Гл. 7]; [2. Гл. 9]; [3. § 7.7]; [5. Гл. 9]; [7. §§ 9.1, 9.2].
Изучаемые вопросы
1. Преобразование Лапласа и его свойства.
2. Теорема разложения.
3. Расчет переходных процессов операторным методом.
4. Операторные передаточные функции.
Пояснения к изучаемым вопросам
1. Обратить внимание на изображения по Лапласу единичной функции, единичной импульсной функции, экспоненциального сигнала.
Для иллюстрации применения свойств преобразования Лапласа рассмотрим два примера.
а). Дано: 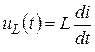 и, что
и, что ![]()
![]()
![]() .
.
Тогда изображение напряжения на индуктивности будет:
![]() .
.
б) Дано: 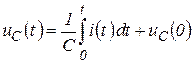 и, что
и, что ![]()
![]()
![]() .
.
Тогда изображение напряжения на емкости будет:
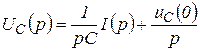 .
.
2. Обратить внимание на формулы (7.30), (7.31) и (7.32), приведенные в [1].
3. Обратить внимание на операторные схемы замещения, закон Ома в операторной форме и законы Кирхгофа в операторной форме, рассмотренные в [2. стр. 252 254], и на примеры решения типовых задач в [1, 2, 7].
4. Знать определение операторной передаточной функции, ее свойства, нули и полюсы функции.
Временной метод анализа линейных
электрических цепей
[1. Гл. 8]; [2. Гл. 8]; [3. § 7.9]; [5. Гл. 10]; [6. § 6.3]; [7. Гл. 10].
Изучаемые вопросы
1. Переходные и импульсные характеристики электрических цепей.
2. Интеграл Дюамеля.
3. Интеграл наложения.
Пояснения к изучаемым вопросам
1. В зависимости от вида воздействия (тока или напряжения) и вида реакции цепи переходная и импульсная характеристики цепи могут быть безразмерными величинами либо иметь размерность А/В либо В/А. Практически переходная характеристика рассчитывается, как переходный процесс в виде тока или напряжения, вызванный включением цепи с нулевыми начальными условиями на постоянное напряжение, равное 1 В.
Импульсная характеристика цепи рассчитывается, как производная от переходной характеристики. При этом необходимо знать, что, если переходная характеристика ![]() имеет скачок при t
= 0, т.е.
имеет скачок при t
= 0, т.е. ![]() , то импульсная характеристика будет иметь вид
, то импульсная характеристика будет иметь вид
![]() ,
,
где ![]() – импульсная функция.
– импульсная функция.
2. Интеграл Дюамеля отражает принцип наложения при анализе электрических цепей, служит главным образом для расчета реакции цепей на непериодические сигналы произвольной формы. В качестве временной функции цепи используется переходная характеристика цепи. Характерной особенностью аппарата интеграла Дюамеля является то, что при расчете реакции цепи на сигналы, имеющие скачкообразный характер изменения, каждый такой скачок отражается дополнительным слагаемым в записи реакции. При этом число участков интегрирования определяется числом участков, на которых функция входного сигнала непрерывна и дифференцируема.
3. В интеграле наложения в качестве временной функции цепи используется ее импульсная характеристика. Это, в отличие от интеграла Дюамеля, позволяет исключить дополнительные слагаемые при записи реакции цепей на сигналы, имеющие скачкообразный характер изменения. Однако, если импульсная характеристика имеет слагаемое с импульсной функцией ![]() (см. выше п. 1), то исходное выражение интеграла наложения становится более сложным (см. типовую задачу 3.2).
(см. выше п. 1), то исходное выражение интеграла наложения становится более сложным (см. типовую задачу 3.2).
Спектральный (частотный) метод анализа
линейных электрических цепей
[1. §§ 5.1, 5.3, Гл. 9]; [2. § 7.1, задача 7.2, Гл. 10]; [3. §§ 6.1, 6.3]; [6. §§ 2.3, 2.4, 2.6, 2.8 2.13, 6.2]; [5. § 7.1, 7.2, 10.6, Гл. 11]; [8. стр. 81 111]; [7. Гл. 11].
Изучаемые вопросы
1. Периодические негармонические сигналы. Разложение в ряд Фурье.
2. Интеграл Фурье.
3. Основные теоремы спектрального анализа.
4. Распределение энергии в спектре непериодического сигнала.
5. Спектры типовых сигналов.
6. Спектральный анализ цепей при непериодических сигналах.
7. Условие безыскаженной передачи сигналов через линейную цепь.
8. Связь между временными и частотными характеристиками электрических цепей.
Пояснения к изучаемым вопросам
1. Периодические негармонические сигналы (сигналы произвольной формы) описываются соответствующими функциями времени. Такие функции, если они удовлетворяют условиям Дирикле, могут быть разложены в ряд Фурье:
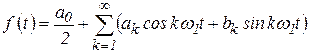 , (1)
, (1)
где ![]() ; Т
– период колебаний;
; Т
– период колебаний; ![]() ,
, ![]() и
и ![]() – коэффициенты разложения, равные:
– коэффициенты разложения, равные:
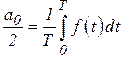 ;
; 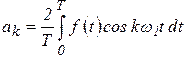 ;
; 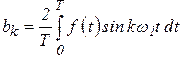 .
.
Целью разложения в ряд Фурье является получение амплитудного и фазового спектров сигнала. Эти спектры могут быть найдены путем преобразования формулы (1). Следует обратить внимание на то, что преобразования выполняются по-разному. Так в [1, 3, 8] ряд Фурье представлен в виде
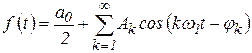 , (2)
, (2)
где ![]() – амплитуда k
-ой гармоники;
– амплитуда k
-ой гармоники; ![]() – фаза k
-ой гармоники.
– фаза k
-ой гармоники.
В [2] получено:
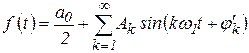 , (3)
, (3)
где ![]() – амплитуда k
-ой гармоники;
– амплитуда k
-ой гармоники; ![]() – фаза k
-ой гармоники.
– фаза k
-ой гармоники.
Из анализа (2) и (3) видно, что от вида преобразования амплитуды гармоник спектра сигнала от частоты не зависят, а зависят только начальные фазы гармоник.
Необходимо хорошо представлять амплитудный спектр периодических прямоугольных импульсов. Помнить, что частоты спектральных составляющих определяются периодом следования импульсов, нули огибающей спектра определяются длительностью импульса, а сам спектр носит дискретный характер.
2. Интеграл Фурье служит для спектрального описания непериодических сигналов произвольной формы. При этом находятся не амплитуды спектральных составляющих (теоретически они существуют, но их количество равно бесконечности, а амплитуды являются бесконечно малыми величинами), а определяется спектральная плотность сигнала – новая физическая величина, которая имеет размерность [B c]. Спектральная плотность является модулем комплексной спектральной плотности (спектральной функции) сигнала и находится с помощью прямого преобразования Фурье.
Следует помнить, что непериодический сигнал в отличие от периодического имеет сплошной или непрерывный спектр.
3. Учитывая, что преобразование Фурье есть частный случай преобразования Лапласа, если принять ![]() , то свойства и теоремы у них должны быть аналогичны. Наиболее важное значение имеют свойство линейности, теорема о задержке сигнала, изменение масштаба независимой переменной, теорема свертки, дифференцирование и интегрирование сигнала, смещение спектра сигнала по частоте.
, то свойства и теоремы у них должны быть аналогичны. Наиболее важное значение имеют свойство линейности, теорема о задержке сигнала, изменение масштаба независимой переменной, теорема свертки, дифференцирование и интегрирование сигнала, смещение спектра сигнала по частоте.
5. Необходимо знать спектры следующих сигналов: единичной функции, единичной импульсной функции, гармонического колебания, постоянной составляющей функции, одиночного прямоугольного импульса (видеоимпульса), радиоимпульса.
7. Необходимо знать не только условия безискаженной передачи сигналов через электрическую цепь, но и уметь объяснить как изменяется форма, например, скачка напряжения или прямоугольного импульса, если ограничить полосу пропускания цепи.
8. Временной и спектральный (частотный) анализ цепей – это решение одной и той же задачи, расчета прохождения сигнала через электрическую цепь, путем использования различного математического аппарата. Очевидно, что эти два метода анализа цепей связаны между собой. Наиболее наглядно это выражается в, легко доказываемой, связи между импульсной характеристикой цепи ![]() и комплексной передаточной функцией
и комплексной передаточной функцией ![]() :
:
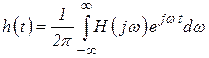 ;
;
и 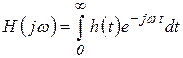 .
.
Нелинейные цепи при гармонических воздействиях
[1. § 10.2, Гл. 11]; [3. §§ 12.3 12.5]; [4. Гл. 3]; [6. §§ 8.3, 8.5]; [8. стр. 136 149].
Изучаемые вопросы
1. Аппроксимация вольт-амперных характеристик (ВАХ) нелинейных элементов (НЭ).
2. Воздействие гармонического колебания на НЭ.
3. Воздействие суммы гармонических колебаний на цепь с НЭ.
Пояснения к изучаемым вопросам
1. Выбор вида аппроксимации ВАХ НЭ зависит от рабочего участка ВАХ. Последний зависит от выбора рабочей точки на характеристике и размаха переменной составляющей сигнала относительно рабочей точки. Наиболее часто используются степенная (полиномиальная) и кусочно-линейная аппроксимации.
2. В общем случае нелинейность ВАХ НЭ приводит к тому, что форма тока НЭ не повторяет форму входного воздействия. Так, если входным является гармоническое напряжение, а НЭ работает в режиме с отсечкой, то ток НЭ будет иметь форму косинусоидальных импульсов. Ток такой формы, в свою очередь, имеет сложный спектральный состав, состоящий из гармонических колебаний с частотами кратными входной, т.е. ток насыщен высшими гармониками частоты входного сигнала.
Если ВАХ НЭ имеет участок с практически линейной зависимостью, а входной сигнал не выходит за пределы этого участка, то аппроксимация ВАХ может быть выполнена полиномом первой степени вида:
![]() ,
,
где ![]() и
и ![]() – координаты рабочей точки на входной ВАХ НЭ;
– координаты рабочей точки на входной ВАХ НЭ; ![]() – крутизна ВАХ в рабочей точке; u
– переменное входное напряжение. В этом случае форма выходного тока НЭ будет повторять форму входного напряжения, например, гармонического.
– крутизна ВАХ в рабочей точке; u
– переменное входное напряжение. В этом случае форма выходного тока НЭ будет повторять форму входного напряжения, например, гармонического.
3. Необходимо уметь объяснить, что при воздействии на НЭ суммы двух гармонических сигналов с разными частотами, в токе НЭ возникают колебания, имеющие в своем спектре частоты не только кратные входным, но и комбинационные частоты, равные сумме или разности входных.
Цепи с обратной связью. Устойчивость.
[1. Гл. 14]; [2. стр. 365 375]; [5. §§ 9.9, 9.10]; [4. §§ 4.1, 4.2]; [6. §§ 5.8, 5.9, 5.10]; [7. § 9.3].
Изучаемые вопросы
1. Передаточная функция цепи с обратной связью.
2. Примеры цепей с обратной связью.
3. Устойчивость цепи с обратной связью.
Пояснения к изучаемым вопросам
2. В современной схемотехнике довольно часто встречаются схемы на операционных усилителях, в которых используется отрицательная и положительная обратная связь. К устройствам с отрицательной обратной связью относятся масштабные усилители с инвертирующим и неинвертирующим входом, сумматоры, интеграторы, дифференциаторы. Для анализа работы этих устройств можно составить их эквивалентные схемы на базе управляемых источников энергии и воспользоваться, например, методом узловых напряжений, как это выполнено в [1. § 2.7]. Но можно воспользоваться методикой расчета цепей с обратной связью, рассмотренной в [1. § 14.2].
3. Цепь называется устойчивой, если свободные колебания в ней с течением времени стремятся к нулю. Зная передаточную функцию цепи можно узнать является ли исследуемая цепь устойчивой. Для этого используется алгебраический критерий устойчивости Рауса-Гурвица. Более простым является геометрический критерий устойчивости Найквиста, основанный на построении годографа петлевого усиления цепи.
Автоколебательные цепи
[1. Гл. 15]; [3. Гл. 13]; [4. §§ 4.4, 4.5]; [6. §§ 9.1 – 9.11]; [8. стр. 154 – 173].
Изучаемые вопросы
1. Физические процессы в автоколебательных цепях.
2. Обобщенная схема автогенератора.
3. LC - генератор с трансформаторной обратной связью.
4. Трехточечные схемы генераторов.
5. RC -генераторы.
6. Автогенераторы с внутренней обратной связью.
Пояснения к изучаемым вопросам
1. Важно уяснить физический смысл понятия баланса амплитуд с энергетической точки зрения и понятия баланса фаз, как признака положительной обратной связи.
2. Необходимо четко понимать разницу в работе автогенераторов в режиме возникновения колебаний и в стационарном режиме. Анализ этих режимов может быть выполнен классическим методом с помощью дифференциального уравнения генератора или операторным методом с помощью передаточной функции цепи с обратной связью. Во втором случае удобно воспользоваться критерием устойчивости Найквиста.
В автогенераторах с LC
-контурами частота генерации ![]() гармонических колебаний определяется резонансной частотой контура
гармонических колебаний определяется резонансной частотой контура ![]() . Ток нелинейного активного элемента, на котором собрана схема автогенератора, имеет нелинейную зависимость от управляющего напряжения. Управляющим напряжением является напряжение обратной связи
. Ток нелинейного активного элемента, на котором собрана схема автогенератора, имеет нелинейную зависимость от управляющего напряжения. Управляющим напряжением является напряжение обратной связи ![]() , которое имеет гармоническую форму с частотой
, которое имеет гармоническую форму с частотой ![]() . Тогда указанный ток будет насыщен гармониками частоты
. Тогда указанный ток будет насыщен гармониками частоты ![]() . Однако напряжение на LC
-контуре
. Однако напряжение на LC
-контуре ![]() , за счет избирательных свойств контура, создается только первой гармоникой тока с частотой
, за счет избирательных свойств контура, создается только первой гармоникой тока с частотой ![]() . Амплитуда этого напряжения находится через крутизну S
вольт-амперной характеристики (ВАХ) нелинейного элемента:
. Амплитуда этого напряжения находится через крутизну S
вольт-амперной характеристики (ВАХ) нелинейного элемента:
![]() ,
,
где ![]() – сопротивление контура на резонансной частоте;
– сопротивление контура на резонансной частоте; ![]() – средняя крутизна ВАХ, рассчитанная как отношение первой гармоники тока к амплитуде напряжения
– средняя крутизна ВАХ, рассчитанная как отношение первой гармоники тока к амплитуде напряжения ![]() . Практически среднюю крутизну определяют методом «трех ординат» [4, 6].
. Практически среднюю крутизну определяют методом «трех ординат» [4, 6].
Выбор рабочей точки на ВАХ нелинейного элемента определяет характер зависимости ![]() от
от ![]() . Последнее, в свою очередь, определяет два режима самовозбуждения автогенераторов – мягкий и жесткий, а также устойчивость стационарного режима.
. Последнее, в свою очередь, определяет два режима самовозбуждения автогенераторов – мягкий и жесткий, а также устойчивость стационарного режима.
4. Из схем автогенераторов с LC -контурами наиболее широкое применение находят трехточечные схемы: емкостная трехточка (чаще) и индуктивная (реже, т.к. имеет две индуктивности и один конденсатор).
Вопросы для самоконтроля
1. Законы коммутации.
2. Понятие переходного, установившегося, свободного режимов.
3. Анализ переходных процессов в цепях первого порядка классическим методом.
4. Анализ переходных процессов в цепях второго порядка классическим методом.
5. Преобразование Лапласа и сущность операторного метода расчета
6. Изображения простейших функций.
7. Основные свойства преобразования Лапласа.
8. Законы Ома и Кирхгофа в операторной форме. Операторная схема замещения.
9. Теорема разложения.
10. Последовательность расчета переходных процессов операторным методом.
11. Дифференцирующие и интегрирующие цепи.
12. Временной метод анализа. Единичная ступенчатая функция. Переходная характеристика цепи.
13. Импульсная характеристика цепи.
14. Связь между импульсной и переходной характеристиками.
15. Интеграл наложения.
16. Анализ спектрального состава периодического сигнала.
17. Спектральная плотность непериодических колебаний.
18. Спектр сигнала прямоугольной формы.
19. Передаточные функции пассивных и активных цепей.
20. АЧХ и ФЧХ цепи. Условия безискаженной передачи сигнала через электрическую цепь.
21. Связь между временным и спектральным методами анализа.
22. Операторная передаточная функция. Ее свойства. Полином Гурвица.
23. Степенная и кусочно-линейная аппроксимация характеристик нелинейных элементов.
24. Воздействие гармонического сигнала малых и больших амплитуд на нелинейный элемент.
25. Воздействие суммы гармонических колебаний на цепь с нелинейным элементом.
26. Цепи с обратной связью. Комплексная и операторная передаточная функция цепи с обратной связью.
27. Критерий устойчивости Найквиста.
28. Условия самовозбуждения цепей с обратной связью.
29. Автоколебательные цепи. Физические процессы в автоколебательной цепи.
30. Дифференциальное уравнение автогенератора. Условие самовозбуждения.
31. Стационарный режим работы автогенератора.
32. Примеры автогенераторов (емкостная и индуктивная трехточки, RC -генераторы на мосте Вина и с лестничной цепью обратной связи).
Разделы, изучаемые в шестом семестре
Основы теории четырехполюсников
[1. Гл. 12]; [2. Гл. 12]; [3. Гл. 9]; [5. Гл. 12]; [7. Гл. 12].
Изучаемые вопросы
1. Общие положения.
2. Уравнения передачи четырехполюсника.
3. Применение матриц к расчету четырехполюсников.
4. Параметры холостого хода и короткого замыкания.
5. Характеристические параметры четырехполюсника.
6. Внешние характеристики четырехполюсника.
Пояснения к изучаемым вопросам
2. Помимо уравнений передачи для различных систем параметров четырехполюсников (ЧП), необходимо знать свойства параметров-коэффициентов.
3. Необходимо уметь записывать уравнения передачи ЧП в матричной форме и рассчитывать каскадное соединение ЧП путем перемножения матриц.
4. Входное сопротивление ЧП может рассчитываться (имеет смысл) только при наличии нагрузки ЧП.
Цепи с распределенными параметрами
[1. Гл. 13]; [2. Гл. 11]; [3. Гл. 11]; [5. Гл. 12]; [7. Гл. 13, Гл. 14].
Изучаемые вопросы
1. Общие положения.
2. Уравнения передачи однородной линии.
3. Падающие и отраженные волны.
4. Вторичные параметры однородной линии.
5. Входное сопротивление линии.
6. Линия без потерь.
Пояснения к изучаемым вопросам
2. Первичные параметры линии – это параметры отнесенные к единице длины линии: сопротивление, индуктивность, емкость и проводимость. Если Эти параметры неизменны по всей длине линии, то такая линия называется однородной. Уравнения передачи однородной длинной линии аналогичны уравнениям передачи симметричных ЧП.
3. Учитывая, что в литературе нет однозначности в названиях различных волн в линиях, следует иметь ввиду, что падающая – это прямая волна, а отраженная – это обратная волна.
Коэффициент отражения в конце линии обозначается по разному s или р или r и определяется выражением:
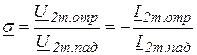 ,
,
где ![]() и
и ![]() – комплексные амплитуды напряжения и тока отраженной волны в конце линии;
– комплексные амплитуды напряжения и тока отраженной волны в конце линии; ![]() и
и ![]() – комплексные амплитуды напряжения и тока падающей волны в конце линии.
– комплексные амплитуды напряжения и тока падающей волны в конце линии.
4. К вторичным параметрам однородной линии относятся волновое сопротивление ![]() и коэффициент распространения
и коэффициент распространения ![]() .
.
В согласованном режиме работы линии, когда сопротивление нагрузки равно волновому ![]() , в линии отсутствуют отраженные волны, а падающая волна называется бегущей.
, в линии отсутствуют отраженные волны, а падающая волна называется бегущей.
6. Линия без потерь – это идеализированная цепь с распределенными параметрами, в которой отсутствуют сопротивление R и проводимость G . Такая идеализация допустима для коротких по длине линий, в который R w L и R wС . В режимах холостого хода или короткого замыкания волны напряжения или тока в линиях без потерь называются стоячими волнами.
Аналоговые электрические фильтры
[1. Гл. 17]; [2. Гл. 15]; [5. Гл. 17 – 20]; [3. Гл. 10]; [7. Гл. 18].
Изучаемые вопросы
1. Классификация фильтров.
2. Аппроксимация характеристик фильтров нижних частот.
3. Преобразование частоты и его применение при синтезе фильтров.
4. Лестничные LC -фильтры.
5. Активные RC -фильтры.
Пояснения к изучаемым вопросам
2. Синтез фильтров состоит из этапа аппроксимации и этапа реализации. На первом этапе исходные требования к фильтру с заданной полосой пропускания пересчитываются в требования к фильтру-прототипу, в качестве которого обычно используется фильтр нижних частот. И уже для фильтра-прототипа формируется передаточная функция. По виду аппроксимирующей функции ослабления различают полиномиальные фильтры – фильтры Баттерворта, Чебышева и фильтры Золотарева со всплесками ослабления.
3. Преобразование частоты тоже относится к этапу аппроксимации. При этом из передаточной функции фильтра-прототипа нижних частот получают передаточную функцию заданного фильтра.
4. На этапе реализации пассивных фильтров создается схема фильтра-прототипа и находятся нормированные значения его элементов. При реализации по Кауэру схема представляет лестничную LC- структуру. Затем схема прототипа трансформируется в схему заданного фильтра, состоящую также только из L и С элементов. Путем денормирования определяются реальные значения элементов.
5. Реализация активных RC -фильтров отличается тем, что для каждого типа фильтров: полосового, нижних или верхних частот существуют свои индивидуальные схемы. А RC -реализация осуществляется в виде каскадного соединения А RC -звеньев второго порядка. Звенья первого порядка чаще бывают пассивными.
Амплитудные и фазовые корректоры
[1. §§ 18.1, 18.2, 18.3]; [2. Гл. 16]; [5. Гл. 22]; [7. § 19.2].
Изучаемые вопросы
1. Принцип корректирования линейных искажений.
2. Амплитудные корректоры.
3. Фазовые корректоры первого порядка.
Пояснения к изучаемым вопросам
1. Необходимо вспомнить условия неискаженной передачи сигналов через линейную цепь.
2. Рассматриваются схемы пассивных корректоров первого и второго порядков. (Г и Т-образные перекрытые схемы).
Дискретные цепи и сигналы
[1. Гл. 19]; [6. §§ 12.1 12.3, 12.5 12.7].
Изучаемые вопросы
1. Дискретные сигналы.
2. Дискретные цепи и элементы дискретных цепей.
3. Z -преобразование дискретной последовательности.
4. Операторные передаточные функции для дискретных цепей.
5. Анализ дискретных сигналов и систем в частотной области.
6. Методы синтеза нерекурсивных и рекурсивных фильтров.
Пояснение к изучаемым вопросам
1. На основании теоремы Котельникова аналоговые сигналы, спектр которых ограничен высшей частотой ![]() , могут быть представлены последовательностью своих дискретных значений (отсчетов), взятых через интервал времени
, могут быть представлены последовательностью своих дискретных значений (отсчетов), взятых через интервал времени ![]() . Тогда
. Тогда ![]() – называется частотой дискретизации.
– называется частотой дискретизации.
Виды типовых дискретных сигналов: дискретная единичная импульсная функция; дискретная единичная функция; дискретные косинусоида и синусоида.
2. Основными элементами дискретных цепей являются: сумматор последовательностей; умножитель на постоянный коэффициент; элемент задержки, выход которого равен входной выборке задержанной на один интервал дискретизации.
Дискретную цепь по аналогии с аналоговой можно описать дискретной импульсной характеристикой, которая является реакцией цепи на дискретную импульсную функцию. Тогда реакция цепи на дискретный сигнал произвольной формы может быть найдена с помощью дискретной свертки.
3. Z -преобразование дискретной последовательности тождественно преобразованию Лапласа для аналоговых сигналов. Z -представление несет информацию о дискретном сигнале: величину отсчета и номер отсчета, соответствующий моменту времени, когда действует этот отсчет.
|
Рис. 1 |
4. Операторная передаточная функция для дискретных цепей еще называется системной функцией. Эта функция связывает Z -преобразования входного и выходного дискретных сигналов.
5. Если дискретный сигнал подвергнуть преобразованию Фурье, то окажется, что он будет иметь «сплошной» периодический спектр с периодом повторения, равным частоте дискретизации (рис. 1). Спектр дискретного сигнала позволяет оценить оптимальность формулы для частоты дискретизации ![]() аналогового сигнала, имеющего максимальную частоту спектра
аналогового сигнала, имеющего максимальную частоту спектра ![]() . Показателем является то, насколько достоверно восстанавливается аналоговый сигнал по отсчетам дискретизированного сигнала. Обычно восстановление осуществляется с помощью ФНЧ, частота среза которого равна
. Показателем является то, насколько достоверно восстанавливается аналоговый сигнал по отсчетам дискретизированного сигнала. Обычно восстановление осуществляется с помощью ФНЧ, частота среза которого равна ![]() .
.
Если ![]() (рис. 1 а
), то дискретизированный сигнал восстанавливается без искажения при условии, что АЧХ ФНЧ близка к идеальной (прямоугольной). Если
(рис. 1 а
), то дискретизированный сигнал восстанавливается без искажения при условии, что АЧХ ФНЧ близка к идеальной (прямоугольной). Если ![]() (рис. 1 б
), то получаем взаимное перекрытие спектральных кривых в области
(рис. 1 б
), то получаем взаимное перекрытие спектральных кривых в области ![]() , что неизбежно приведет к искажению информации о форме аналогового сигнала в ходе его дискретизации. Если
, что неизбежно приведет к искажению информации о форме аналогового сигнала в ходе его дискретизации. Если ![]() (рис. 1 в
), то взаимное перекрытие соседних областей спектра исключается в принципе. Это позволяет избежать погрешности восстановления аналогового сигнала при низкой избирательности ФНЧ.
(рис. 1 в
), то взаимное перекрытие соседних областей спектра исключается в принципе. Это позволяет избежать погрешности восстановления аналогового сигнала при низкой избирательности ФНЧ.
Необходимо понимать, что если дискретный сигнал периодический, то для его анализа используется дискретное преобразование Фурье, которое показывает, что спектр такого сигнала будет тоже дискретным и периодическим.
6. Следует знать отличие в методах синтеза рекурсивных цифровых фильтров и нерекурсивных. Уметь объяснить суть метода билинейного преобразования для синтеза рекурсивных фильтров. Знать алгоритм расчета фильтра на этапе аппроксимации, когда получают операторную передаточную функцию фильтра. При рассмотрении этапа реализации фильтров уметь объяснить работу схем рекурсивных и нерекурсивных цифровых фильтров.
Вопросы для самоконтроля
1. Уравнения передачи четырехполюсников в Z , Y и А -параметрах в алгебраической и матричной форме.
2. Параметры холостого хода и короткого замыкания четырехполюсников.
3. Входное и характеристические сопротивления четырехполюсников.
4. Характеристическая постоянная передачи четырехполюсника.
5. Рабочая постоянная передачи четырехполюсника.
6. Цепи с распределенными параметрами. Основные понятия. Первичные параметры.
7. Уравнения передачи длинной однородной линии.
8. Падающие и отраженные волны в длинных линиях. Коэффициент отражения.
9. Вторичные параметры однородной линии.
10. Входное сопротивление длинной линии.
11. Линия без потерь в режимах согласованного включения, холостого хода и короткого замыкания.
12. Классификация электрических фильтров.
13. Постановка задачи синтеза электрических фильтров. Сущность этапов аппроксимации и реализации фильтров.
14. Фильтры Баттерворта, Чебышева, Золотарева. Достоинства и недостатки их.
15. Преобразование частоты при синтезе фильтров.
16. Лестничные LC -фильтры.
17. Активные RC -фильтры.
18. Задача амплитудной и фазовой коррекции в электрических цепях.
19. Амплитудные корректоры первого и второго порядков.
20. Дискретизация аналоговых сигналов. Цели и основные понятия и определения.
21. Элементы дискретных цепей.
22. Дискретная импульсная функция и дискретная импульсная характеристика цепи. Дискретная свертка.
23. Z -преобразование дискретных сигналов.
24. Системная (передаточная) функция дискретных цепей.
25. Спектры дискретных сигналов непериодических и периодических.
26. Синтез рекурсивных и нерекурсивных дискретных фильтров.
КОНТРОЛЬНЫЕ ЗАДАНИЯ И ПОРЯДОК
ИХ ВЫПОЛНЕНИЯ
Выбор варианта
Контрольные задания составлены в ста вариантах.
Каждый студент выполняет контрольное задание по одному из вариантов в соответствии с номером своего студенческого билета: номер варианта совпадает с числом, образованном двумя последними цифрами студенческого билета. Например, студенческому билету № 90237 соответствует вариант № 37, а студенческому билету № 96740 соответствует вариант № 40.
На третьем курсе студент должен выполнить две контрольные работы (№ 3 и № 4).
Требования к оформлению контрольных работ
1. Контрольная работа выполняется каждая в отдельной ученической тетради. Она должна быть аккуратно и разборчиво написана чернилами на одной стороне каждого листа тетради, т.е. на правой стороне развернутой тетради. Левая сторона оставляется чистой, между строками записи рекомендуем оставлять пробел, а на краю листа – поля (2 ... 3 см). Это облегчит рецензенту работы отметить ошибки и объяснить их как раз в том месте, где они оказались. Все исправления по замечаниям рецензии рекомендуем выполнять прямо в тексте, где это возможно. Чтобы была видна ваша работа по замечаниям рецензии, можно все исправления выполнять чернилами другого цвета. Где исправления в тексте выполнить невозможно, можно показать верный ход расчета на оставлявшейся пустой левой стороне развернутой тетради на соответствующей странице или добавить вклейки. Выполнять исправления в конце тетради не рекомендуется!
2. Все страницы тетради должны быть пронумерованы. Нумеруются также все рисунки и таблицы решений. Графики и схемы удобно выполнить на вклейках миллиметровой бумаги. Чертежи могут быть выполнены и карандашом. Необходимо соблюдать правила черчения и ГОСТы.
3. Масштабы всех графиков должны быть равномерными. Неравномерные, например, полулогарифмические или логарифмические масштабы не допускаются. Масштаб должен быть показан вдоль осей равномерными круглыми цифровыми метками (например: 0,2; 0,4 и т.д.). В конце осевых линий графика указывают отложенную величину и используемые для меток единицы (например, u , B или t , с).
4. Решение каждой задачи должно начинаться с перечерчивания схемы задания для Вашего варианта. По требуемому варианту должны быть выписаны все численные данные задания.
5. Все величины: сопротивления, э.д.с., напряжения, токи и т.д., – буквенные обозначения которых применяются в ходе решения, должны быть показаны хотя бы на одной из схем, сопровождающих решение. Принятые обозначения нельзя менять в ходе решения одной задачи. Нельзя в одной задаче одинаково обозначить разные величины!
6. Исходные соотношения должны быть вначале записаны в буквенном виде. Однако надо стремиться избегать алгебраических буквенных преобразований. Обычно решение значительно легче проводится с численными алгебраическими преобразованиями, когда уже в исходные уравнения задачи подставлены конкретные числовые значения взамен буквенным обозначениям коэффициентов.
7. Следует иметь в виду, что в промежуточных формулах наименование размерных единиц обычно не указывается. Однако размерность окончательных численных результатов должна быть указана обязательно. Не принято указывать размерности изображений операторного метода. При расчетах операторным методом следует всегда применять основные единицы системы СИ.
8. Расчетные значения допускается округлять до первых трех значащих цифр.
9. На обложке тетради должен быть наклеен адресный бланк, а на первой странице – титульный бланк. В конце работы указывается использованная литература, список которой должен соответствовать требованиям ГОСТ 7.1 – 76 (см., например, список литературы настоящей документации). На последней странице решения должна быть подпись студента.
КОНТРОЛЬНАЯ РАБОТА № 3
Задача 3.1
Задача посвящена анализу переходного процесса в цепи первого порядка, содержащей резисторы, конденсатор или индуктивность. В момент времени t = 0 происходит переключение ключа К , в результате чего в цепи возникает переходной процесс.
1. Перерисуйте схему цепи (см. рис. 3.1) для Вашего варианта (таблица 1).
2. Выпишите числовые данные для Вашего варианта (таблица 2).
3. Рассчитайте все токи и напряжение на С
или L
в три момента времени t
: ![]() ,
, ![]() , .
, .
4. Рассчитайте классическим методом переходный процесс в виде ![]() ,
, ![]() ,
, ![]() в схемах 1 – 5,
в схемах 1 – 5, ![]() ,
, ![]() ,
, ![]() в схемах 6 – 10. Проверьте правильность расчетов, выполненных в п. 4, путем сопоставления их с результатами расчетов в п. 3.
в схемах 6 – 10. Проверьте правильность расчетов, выполненных в п. 4, путем сопоставления их с результатами расчетов в п. 3.
5. Постройте графики переходных токов и напряжения, рассчитанных в п. 4. Определите длительность переходного процесса, соответствующую переходу цепи в установившееся состояние с погрешностью 5%.
6. Рассчитайте ток ![]() операторным методом.
операторным методом.
Таблица 1
| Варианты |
Номер схемы или задания |
| 00 10 20 30 40 50 60 70 80 90 01 11 21 31 41 51 61 71 81 91 02 12 22 32 42 52 62 72 82 92 03 13 23 33 43 53 63 73 83 93 04 14 24 34 44 54 64 74 84 94 05 15 25 35 45 55 65 75 85 95 06 16 26 36 46 56 66 76 86 96 07 17 27 37 47 57 67 77 87 97 08 18 28 38 48 58 68 78 88 98 09 19 29 39 49 59 69 79 89 99 |
1 2 3 4 5 6 7 8 9 10 |
|
Рис. 3.1 |
Таблица 2
| Варианты |
С , нф или L , мГн |
|
|
|
Е , В |
| От 00 до 09 От 10 до 19 От 20 до 29 От 30 до 39 От 40 до 49 От 50 до 59 От 60 до 69 От 70 до 79 От 80 до 89 От 90 до 99 |
20 10 10 15 15 15 20 20 15 10 |
2 1 1 1 2 1 2 2 1 0,5 |
2 1 2 1 2 2 1 1 0,5 1 |
2 1 2 2 1 1 2 1 0,5 1 |
10 5 12 12 10 10 12 12 5 5 |
Типовая задача Т3.1
Цепь (рис. 3.2 а
) содержит резисторы ![]() = 1 кОм,
= 1 кОм, ![]() = 1,5 кОм,
= 1,5 кОм, ![]() = = 0,5 кОм,
= = 0,5 кОм, ![]() = 2,5 кОм, индуктивность L
= 6,3 мГн и источник постоянного напряжения Е
= 9 В. В момент t
= 0 происходит размыкание ключа К
и в цепи возникает переходной процесс. Требуется: рассчитать основные характеристики процесса; получить выражения для токов
= 2,5 кОм, индуктивность L
= 6,3 мГн и источник постоянного напряжения Е
= 9 В. В момент t
= 0 происходит размыкание ключа К
и в цепи возникает переходной процесс. Требуется: рассчитать основные характеристики процесса; получить выражения для токов ![]() ,
, ![]() и напряжения
и напряжения ![]() классическим методов; построить графики указанных токов и напряжений; рассчитать ток
классическим методов; построить графики указанных токов и напряжений; рассчитать ток ![]() операторным методом.
операторным методом.
Решение
1. Находим токи ![]() ,
, ![]() ,
, ![]() и напряжение
и напряжение ![]() в три момента времени t
=
в три момента времени t
= ![]() ,
, ![]() и .
и .
1.1. Момент t
= ![]() . Он соответствует стационарному состоянию цепи до коммутации. В этом состоянии резистор
. Он соответствует стационарному состоянию цепи до коммутации. В этом состоянии резистор ![]() закорочен ключом К
и не влияет на работу цепи. Сама схема (рис. 3.2 а
) представляет собой цепь, в которой
закорочен ключом К
и не влияет на работу цепи. Сама схема (рис. 3.2 а
) представляет собой цепь, в которой ![]() = 0, поэтому она может быть рассчитана по следующим формулам:
= 0, поэтому она может быть рассчитана по следующим формулам:
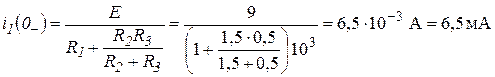 ;
;
|
Рис. 3.2 |
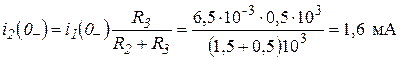 ;
;
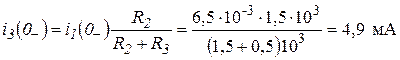 .
.
1.2. Момент t
= ![]() . Это первое мгновение после размыкания ключа. В соответствие с законом коммутации
. Это первое мгновение после размыкания ключа. В соответствие с законом коммутации
![]() . (3.1)
. (3.1)
Остальные величины находим путем составления и решения системы уравнений по законам Кирхгофа, описывающих электрическое состояние цепи в момент ![]() (рис. 3.2 б
):
(рис. 3.2 б
):
 .
.
После числовых подстановок с учетом (3.1) получим:
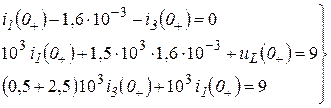 .
.
Решая систему, находим:
![]() ,
, ![]() ,
, ![]() . (3.2)
. (3.2)
1.3. Момент t
= . Означает новое стационарное состояние цепи после окончания переходного процесса. Внешне схема цепи при t
= соответствует рис. 3.2 б
, причем ![]() , а токи рассчитываются по формулам:
, а токи рассчитываются по формулам:
|
Рис. 3.3 |
 ;
;
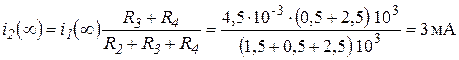 ;
;
![]() .
.
2. Расчет токов ![]() ,
, ![]() и напряжения
и напряжения ![]() после коммутации классическим методом.
после коммутации классическим методом.
Переходный процесс в цепях первого порядка (с одним реактивным элементом) описывается уравнением вида
![]() , (3.3)
, (3.3)
где ![]() – принужденная составляющая искомой величины, равная ее значению при t
= ;
– принужденная составляющая искомой величины, равная ее значению при t
= ; ![]() – свободная составляющая; A
– постоянная интегрирования; р
– корень характеристического уравнения, определяющий в конечном итоге длительность переходного процесса. Так как р
является общей величиной для всех токов и напряжений в конкретной цепи, то расчет переходного процесса целесообразно начать с определения р
.
– свободная составляющая; A
– постоянная интегрирования; р
– корень характеристического уравнения, определяющий в конечном итоге длительность переходного процесса. Так как р
является общей величиной для всех токов и напряжений в конкретной цепи, то расчет переходного процесса целесообразно начать с определения р
.
2.1. Характеристическое уравнение для расчета р составляется по операторной схеме замещения, отражающей работу цепи после коммутации, и показанной на рис. 3.3.
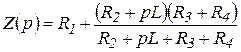 .
.
Принимая ![]() 0, получим характеристическое уравнение
0, получим характеристическое уравнение
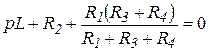 .
.
Решение уравнения дает корень
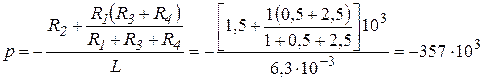 . (3.4)
. (3.4)
Величина 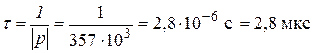 (3.5) называется постоянной времени цепи.
(3.5) называется постоянной времени цепи.
2.2. Расчет ![]() .
.
В соответствии с (3.3) запишем:
![]() .
.
Учтем, что ![]() . Величину
. Величину ![]() найдем из рассмотрения
найдем из рассмотрения ![]() с учетом независимого начального условия (3.1):
с учетом независимого начального условия (3.1):
![]() .
.
Откуда ![]() = 1,6 – 3 = –1,4. Тогда
= 1,6 – 3 = –1,4. Тогда
![]() . (3.6)
. (3.6)
2.3. Расчет ![]() .
.
Воспользуемся законом Ома для индуктивности
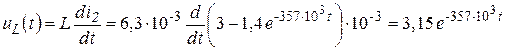 . (3.7)
. (3.7)
2.4. Расчет ![]() . Ведется аналогично расчету
. Ведется аналогично расчету ![]() .
.
![]() .
.
![]() .
.
![]() . (3.8)
. (3.8)
2.5. Проверка правильности расчетов производится путем анализа выражений (3.6), (3.7) и (3.8) в моменты времени t = 0 и .
![]() ;
; ![]() .
.
![]() ;
; ![]() .
.
![]() ;
; ![]() .
.
Полученные значения всех величин совпадают с результатами расчетов в п. 1.
3. Построение графиков переходного процесса.
Для построения графиков необходимо составить таблицу значений ![]() ,
, ![]() ,
, ![]() в различные моменты времени (таблица 3).
в различные моменты времени (таблица 3).
Таблица 3
| t |
0 |
0,5t |
t |
1,5t |
2t |
3t |
4t |
| t , мкс |
0 |
1,4 |
2,8 |
4,2 |
5,6 |
8,4 |
11,2 |
|
|
1,6 |
2,16 |
2,5 |
2,7 |
2,8 |
2,93 |
2,97 |
|
|
1,85 |
1,71 |
1,63 |
1,58 |
1,54 |
1,51 |
1,5 |
|
|
3,15 |
1,9 |
1,16 |
0,7 |
0,41 |
0,16 |
0,06 |
Кривые ![]() и
и ![]() могут быть построены на одном графике. При выборе масштабных делений по осям графиков учитываются максимальные значения соответствующих величин. Для тока и напряжения целесообразно принять в 1 см по 1 мА и 1 В соответственно. Масштаб по оси времени определяется длительностью переходного процесса. Известно, что экспоненциальные функции за время t
= 3t
изменяется на 95% от своего максимального значения. Тогда можно принять, что переходный процесс в цепях первого порядка заканчивается через 3t
с погрешностью 5%. Учитывая (3.5), получим для данной схемы
могут быть построены на одном графике. При выборе масштабных делений по осям графиков учитываются максимальные значения соответствующих величин. Для тока и напряжения целесообразно принять в 1 см по 1 мА и 1 В соответственно. Масштаб по оси времени определяется длительностью переходного процесса. Известно, что экспоненциальные функции за время t
= 3t
изменяется на 95% от своего максимального значения. Тогда можно принять, что переходный процесс в цепях первого порядка заканчивается через 3t
с погрешностью 5%. Учитывая (3.5), получим для данной схемы ![]() = 3t
= 8,4 мкс. Для построения графика удобно принять масштаб по оси времени 2 мкс в 1 см.
= 3t
= 8,4 мкс. Для построения графика удобно принять масштаб по оси времени 2 мкс в 1 см.
|
Рис. 3.4 |
4. Расчет тока ![]() операторным методом.
операторным методом.
Для состояния цепи при t
0 (рис. 3.2) составляется операторная схема замещения, которая учитывает независимые начальные условия в виде дополнительных (расчетных) источников напряжения ![]() или
или ![]() . В данной задаче таким источником будет
. В данной задаче таким источником будет ![]() (рис. 3.5).
(рис. 3.5).
Используя закон Ома, в операторной форме, запишем
|
Рис. 3.5 |
 , (3.9)
, (3.9)
где ![]() может быть найдено по методу узловых напряжений:
может быть найдено по методу узловых напряжений:
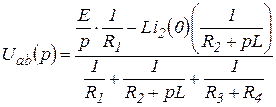 , (3.10)
, (3.10)
Подставляя (3.10) в (3.9), получим
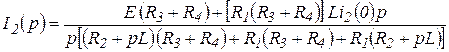 .
.
После числовых подстановок
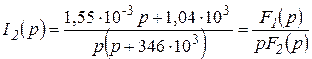 .
.
Используя теорему разложения, найдем оригинал тока:
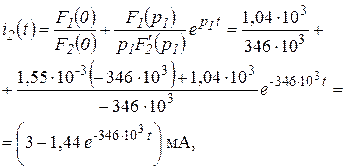
которое совпадает с выражение (3.6), полученным классическим методом.
Задача 3.2
Задача посвящена временному и частотному (спектральному) методам расчета реакции цепей на сигналы произвольной формы. В качестве такого сигнала используется импульс прямоугольной формы (видеоимпульс).
Электрические схемы цепей (рис. 3.6) содержат емкости С
или индуктивности L
, а также сопротивления R
. Для всех вариантов ![]() . В схемах, где имеется сопротивление
. В схемах, где имеется сопротивление ![]() , его величина
, его величина ![]() . Во всех схемах входным напряжением
. Во всех схемах входным напряжением ![]() является прямоугольный импульс длительностью
является прямоугольный импульс длительностью ![]() и амплитудой
и амплитудой ![]() .
.
1. Перерисуйте схему Вашего варианта (см. табл. 1 и рис. 3.6). Выпишите исходные данные Вашего варианта (таблица 4).
Таблица 4
| Варианты |
С , пф или L , мкГн |
|
|
|
| От 00 до 09 От 10 до 19 От 20 до 29 От 30 до 39 От 40 до 49 От 50 до 59 От 60 до 69 От 70 до 79 От 80 до 89 От 90 до 99 |
20 25 30 20 25 30 20 25 30 25 |
1 1 1 2 2 2 3 3 3 2,5 |
30 35 40 35 40 45 35 40 45 35 |
3 4 5 6 7 3 4 5 6 7 |
Временной метод расчета
2. Рассчитайте переходную ![]() и импульсную
и импульсную ![]() характеристики цепи по напряжению классическим или операторным методами (по выбору).
характеристики цепи по напряжению классическим или операторным методами (по выбору).
3. Рассчитайте реакцию цепи в виде выходного напряжений ![]() используя:
используя:
- интеграл Дюамеля;
- интеграл наложения.
4. Постройте временные диаграммы входного и выходного напряжений.
|
Рис. 3.6 |
Частотный метод расчета
5. Рассчитайте комплексные спектральные плотности входного ![]() и выходного
и выходного ![]() сигналов.
сигналов.
6. Рассчитайте и постройте графики модулей ![]() ,
, ![]()
![]() и модуля комплексной передаточной функции цепи
и модуля комплексной передаточной функции цепи ![]() , как функций от циклической частоты f
в диапазоне частот 0
, как функций от циклической частоты f
в диапазоне частот 0 ![]() .
.
Типовая задача Т3.2
Схема цепи, приведенная на рис. 3.7 а
, содержит емкость С
= 10 пф и сопротивления ![]() = 1 кОм,
= 1 кОм, ![]() = 3 кОм. На входе цепи действует прямоугольный импульс (рис. 3.8) длительностью
= 3 кОм. На входе цепи действует прямоугольный импульс (рис. 3.8) длительностью ![]() = 60 нс и амплитудой
= 60 нс и амплитудой ![]() = 4 В. Выполнить расчеты в соответствии с заданием к задаче 3.2.
= 4 В. Выполнить расчеты в соответствии с заданием к задаче 3.2.
Решение
1. Расчет переходной и импульсной характеристик классическим методом.
1.1. Переходная характеристика цепи рассчитывается, как переходной процесс в виде тока или напряжения, вызванный включением цепи с нулевыми начальными условиями на постоянное напряжение 1 В. В соответствие с этим составляется схема включения (рис. 3.7 б
) ,
на которой E
= 1 В. В задаче определяется переходная характеристика ![]() по напряжению относительно выходного контура
по напряжению относительно выходного контура ![]() , поэтому можно записать, что:
, поэтому можно записать, что:
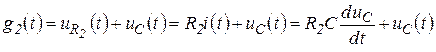 , (3.11)
, (3.11)
Напряжение ![]() в схеме на рис. 3.7 б
может быть рассчитано с помощью общей формулы (3.3) расчета переходных процессов в схемах первого порядка:
в схеме на рис. 3.7 б
может быть рассчитано с помощью общей формулы (3.3) расчета переходных процессов в схемах первого порядка:
|
Рис. 3.7 Рис. 3.8 |
![]() ,
,
где ![]() = 1 В; р
– корень характеристического уравнения, находится из операторного сопротивления схемы
= 1 В; р
– корень характеристического уравнения, находится из операторного сопротивления схемы ![]() , и равен
, и равен ![]() ; постоянная интегрирования находится из рассмотрения
; постоянная интегрирования находится из рассмотрения ![]() при
при ![]() :
:
![]() (нулевое начальное условие).
(нулевое начальное условие).
Откуда ![]() . Окончательно
. Окончательно
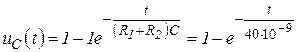 ,
,
где ![]() – постоянная времени цепи.
– постоянная времени цепи.
Подставляя ![]() в (3.11), получим:
в (3.11), получим:
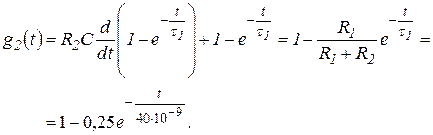 (3.12)
(3.12)
Обратить внимание, что ![]() в (3.12) определяется только элементами цепи и не зависит ни от токов, ни от напряжений.
в (3.12) определяется только элементами цепи и не зависит ни от токов, ни от напряжений.
1.2 Импульсная характеристика цепи h (t ) есть производная от переходной характеристики h (t ) = g (t ). Однако следует учесть, что, если переходная характеристика отлична от нуля при t = 0, т.е. имеет скачок при t = 0, то при дифференцировании появляется дополнительное слагаемое:
h (t ) = g(0)d (t ) + g (t ).
В рассматриваемой задаче ![]() = 0,75, поэтому
= 0,75, поэтому
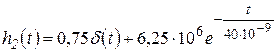 , (3.13)
, (3.13)
где d (t ) – импульсная функция (функция Дирака).
2. Расчет выходного напряжения ![]() временным методов.
временным методов.
2.1. Использование интеграла Дюамеля.
Из известных четырех формул интеграла Дюамеля наиболее общий характер имеет формула вида
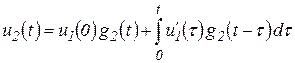 (3.14)
(3.14)
в обозначениях величин и понятий, принятых в рассматриваемой задаче. Переменной интегрирования в (3.14) является t
(не путать с постоянной времени ![]() ).
).
Входное напряжение ![]() имеет форму прямоугольного импульса (рис. 3.8), аналитическая запись которого может быть представлена как
имеет форму прямоугольного импульса (рис. 3.8), аналитическая запись которого может быть представлена как
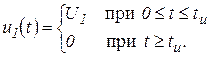 (3.15)
(3.15)
Из (3.15) следует, что ![]() и что производная
и что производная ![]() = 0 или для переменной
= 0 или для переменной ![]() = 0.
= 0.
Число участников интегрирования в (3.14) определяется числом участков в функции, описывающей входной сигнал, в которых она непрерывна и дифференцируема [1, с. 188]. Для функции (3.15) таких участков в виде интервалов времени два: ![]() и
и ![]() . Необходимость учета второго участка, когда
. Необходимость учета второго участка, когда ![]() , объясняется тем, что за время действия импульса в реактивных элементах цепи накапливается энергия электрического и магнитного полей, которая после окончания импульса постепенно убывает до нуля, создавая напряжение и токи в цепи. Анализ этих величин и проводится в интервале
, объясняется тем, что за время действия импульса в реактивных элементах цепи накапливается энергия электрического и магнитного полей, которая после окончания импульса постепенно убывает до нуля, создавая напряжение и токи в цепи. Анализ этих величин и проводится в интервале ![]() .
.
Важнейшей характерной особенностью аппарата интеграла Дюамеля является то, что при записи реакции цепи на каждом новом интервале времени наличие скачкообразного изменения входного сигнала в начальный момент рассматриваемого интервала учитывается дополнительным слагаемым вида
![]() ,
,
где D U – амплитуда скачка;
![]() – момент действия скачка.
– момент действия скачка.
Учитывая сказанное, запишем выходное напряжение цепи в соответствие с (3.14) и (3.12):
для интервала времени ![]()
 . (3.16)
. (3.16)
для интервала времени ![]()
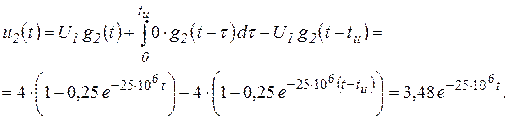 (3.17)
(3.17)
2.2. Использование интеграла наложения.
В отличие от интеграла Дюамеля в интеграле наложения не учитываются дополнительными слагаемыми скачки входного напряжения:
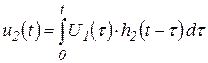 , (3.18)
, (3.18)
С учетом (3.13) реакция (3.18) заданной цепи на прямоугольный импульс будет равна:
для интервала времени ![]()
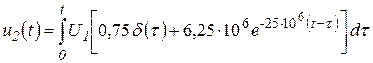 ,
,
Используя фильтрующее свойство импульсной d-функции [1. стр. 173], получим
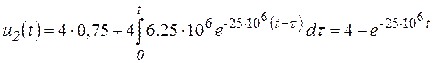 ,
,
Для интервала времени ![]()
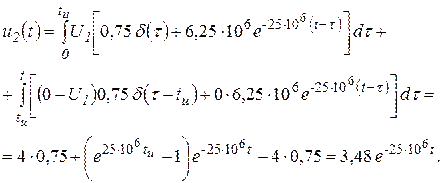
Сравнение результатов расчетов напряжения ![]() с использованием интегралов наложения и Дюамеля показывает, что они совпадают между собой.
с использованием интегралов наложения и Дюамеля показывает, что они совпадают между собой.
3. Построение временной диаграммы входного и выходного напряжений.
Диаграмма выходного напряжения строится с использованием формул (3.16) и (3.17) путем подстановки в них соответствующих моментов времени. Результаты расчетов сводятся в таблицу 5.
Таблица 5
| Время, |
0 |
0,3 |
0,6 |
|
|
|
|
|
| нс |
0 |
18 |
36 |
60 |
60 |
100 |
140 |
180 |
|
|
4 |
4 |
4 |
4 |
0 |
0 |
0 |
0 |
|
|
3 |
3,4 |
3,6 |
3,8 |
0,8 |
0,28 |
0,03 |
0,01 |
|
Рис. 3.9 |
Из таблицы 5 видно, что ![]() в момент
в момент ![]() рассчитывается дважды: при
рассчитывается дважды: при ![]() по формуле (3.16), а при
по формуле (3.16), а при ![]() по формуле (3.17). Именно при такой методике можно определить будет ли скачкообразное изменение в форме выходного сигнала в момент изменения функции, описывающей входной сигнал, как это и показано в рассматриваемом примере.
по формуле (3.17). Именно при такой методике можно определить будет ли скачкообразное изменение в форме выходного сигнала в момент изменения функции, описывающей входной сигнал, как это и показано в рассматриваемом примере.
Выбор расчетных точек в интервале ![]() определяется временем затухающего переходного процесса, которое зависит от постоянной времени цепи, равной
определяется временем затухающего переходного процесса, которое зависит от постоянной времени цепи, равной ![]() = 40 нс.
= 40 нс.
Временные диаграммы входного и выходного напряжений показаны на рис. 3.9.
4. Расчет комплексной спектральной плотности входного ![]() и выходного
и выходного ![]() сигналов.
сигналов.
Для расчета комплексной спектральной плотности непериодического сигнала f (t ) произвольной формы используется прямое преобразование Фурье:
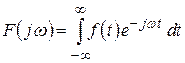 .
.
Для заданного входного сигнала (3.15) преобразование Фурье дает выражение
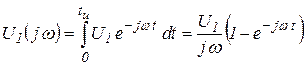 ,
,
которое после преобразований (в контрольной работе показать эти преобразования) принимает более удобную форму
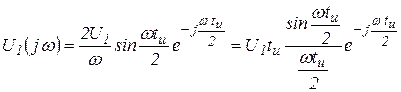 . (3.19)
. (3.19)
Комплексная спектральная плотность выходного сигнала находится по формуле
![]() , (3.20)
, (3.20)
где ![]() – комплексная передаточная функция цепи по напряжению. Функция
– комплексная передаточная функция цепи по напряжению. Функция ![]() находится как отношение комплексного значения гармонического напряжения
находится как отношение комплексного значения гармонического напряжения ![]() на выходе цепи к комплексному значения гармонического напряжения
на выходе цепи к комплексному значения гармонического напряжения ![]() той же частоты, приложенному ко входу цепи:
той же частоты, приложенному ко входу цепи:
![]() .
.
Для схемы, приведенной на рис. 3.7 а легко получить:
 .
.
Тогда
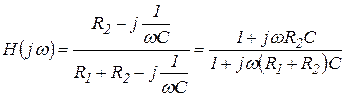 . (3.21)
. (3.21)
Анализ (3.21) позволяет сделать вывод, что комплексная передаточная функция цепи по напряжению определяется только элементами цепи и является безразмерной величиной.
Используя (3.19) и (3.21), находим по (3.20) спектральную плотность выходного сигнала:
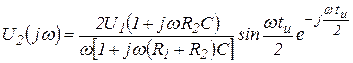 . (3.22)
. (3.22)
5. Расчет графиков модулей ![]() ,
, ![]() и
и ![]() .
.
Из выражений (3.19), (3.21) и (3.22) легко получить модули: спектральной плотности входного напряжения
![]() ; (3.23)
; (3.23)
комплексной передаточной функции (амплитудно-частотная характеристика цепи)
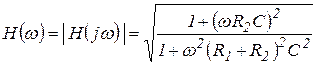 ; (3.24)
; (3.24)
спектральной плотности выходного напряжения
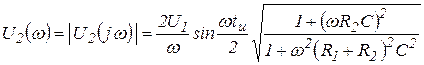 . (3.25)
. (3.25)
|
Рис. 3.10 |
Для построения графиков полученных функций необходимо выбрать расчетные точки по частоте. Учтем, что спектральная плотность одиночного прямоугольного импульса измеряется в вольт секундах [B c] и что она обращается в ноль на частотах ![]() и т.д. Поэтому дополнительно выбираются промежуточные точки между этими частотами. Максимальная частота в соответствие с заданием равна 3/60 10-9
= 50 106
Гц = 50 МГц. Результаты расчетов по (3.23) (3.25) сводим в таблицу 6.
и т.д. Поэтому дополнительно выбираются промежуточные точки между этими частотами. Максимальная частота в соответствие с заданием равна 3/60 10-9
= 50 106
Гц = 50 МГц. Результаты расчетов по (3.23) (3.25) сводим в таблицу 6.
Таблица 6
| f , МГц |
|
|
|
|
| 0 8,3 16,6 24,9 33,3 41,6 50 |
0 52,1 104,2 157 209 261 314 |
240 153 0 51 0 31 0 |
1 0,75 0,75 0,75 0,75 0,75 0,75 |
240 115 0 38 0 23 0 |
По данным таблицы 6 строим графики (рис. 3.10).
Контрольная работа № 4
Задача 4.1
Задача посвящена расчету параметров четырехполюсника (ЧП) и анализу прохождения сигналов через него в согласованном и несогласованном режимах работы.
Электрическая цепь состоит из источника сигнала, имеющего ЭДС ![]() , частоту f
= 5 кГц, начальную фазу
, частоту f
= 5 кГц, начальную фазу ![]() = 40° и внутреннее сопротивление
= 40° и внутреннее сопротивление ![]() , ЧП, собранного по Г-образной схеме с П и Т входом, и нагрузки
, ЧП, собранного по Г-образной схеме с П и Т входом, и нагрузки ![]() (рис. 4.1).
(рис. 4.1).
1. Перерисуйте общую схему (рис. 4.1) и схему ЧП (см. рис. 4.2) для Вашего варианта (таблица 1).
|
Рис. 4.1 |
2. Выпишите из таблицы 2 числовые данные для Вашего варианта (кроме ![]() ).
).
|
Рис. 4.2 |
3 Рассчитайте А -параметры Вашего ЧП, используя табличные соотношения (рис. 4.3).
|
|
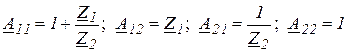 .
.
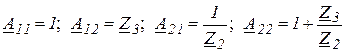 .
.
Рис. 4.3
4. Рассчитайте характеристические параметры ЧП – характеристические сопротивления ![]() и
и ![]() , а также собственную постоянную передачи
, а также собственную постоянную передачи ![]() .
.
5. Рассчитайте входные ![]() и
и ![]() сопротивления ЧП в согласованном режиме, когда
сопротивления ЧП в согласованном режиме, когда ![]() и
и ![]() , и несогласованном режиме, когда
, и несогласованном режиме, когда ![]() , а
, а ![]() .
.
6. Рассчитайте прохождение сигнала е
(t
) в схеме, приведенной на рис. 4.1, в виде напряжений ![]() и
и ![]() и токов
и токов ![]() и
и ![]() в режимах согласованного и несогласованного включения ЧП, а также рабочее ослабление ЧП в обоих режимах. Дайте анализ результатов расчета.
в режимах согласованного и несогласованного включения ЧП, а также рабочее ослабление ЧП в обоих режимах. Дайте анализ результатов расчета.
7. Рассчитайте комплексную передаточную функцию ЧП по напряжению на частоте ![]() = 5 кГц в режиме холостого хода и в рабочем режиме.
= 5 кГц в режиме холостого хода и в рабочем режиме.
Типовая задача Т4.1
|
Рис. 4.4 |
Схема ЧП, приведенная на рис. 4.4, содержит резистор с сопротивлением ![]() = 3 кОм, конденсатор с емкостью
= 3 кОм, конденсатор с емкостью ![]() = 25 нф и индуктивность
= 25 нф и индуктивность ![]() = 25 мГн. В общей схеме включения (рис. 4.1) дан источник сигнала с ЭДС
= 25 мГн. В общей схеме включения (рис. 4.1) дан источник сигнала с ЭДС ![]() В и частотой f
= 5 кГц. Выполнить расчеты, указанные в задаче 4.1.
В и частотой f
= 5 кГц. Выполнить расчеты, указанные в задаче 4.1.
Решение.
1. Расчет А -параметров ЧП.
Заданный ЧП собран по Г-образной схеме с Т-входом. Согласно рис. 4.3 для такой схемы А -параметры находятся по формулам:
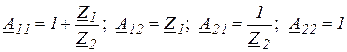 ,
,
где ![]() ;
;
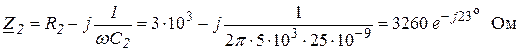 .
.
Тогда получим:
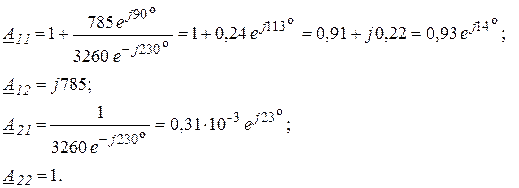
2. Расчет характеристических параметров ЧП.
К характеристическим параметрам ЧП относятся характеристические сопротивления ![]() со стороны зажимов 1 – 1 и
со стороны зажимов 1 – 1 и ![]() со стороны зажимов 2 – 2, а также характеристическая постоянная передачи
со стороны зажимов 2 – 2, а также характеристическая постоянная передачи ![]() . Они могут быть найдены с помощью А
-параметров:
. Они могут быть найдены с помощью А
-параметров:
 Ом;
Ом;
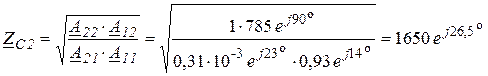 Ом;
Ом;
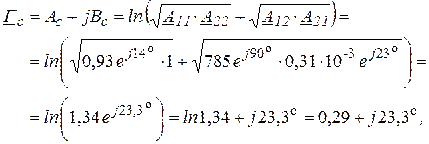
где ![]() – характеристическое ослабление;
– характеристическое ослабление;
![]() – характеристическая фазовая постоянная.
– характеристическая фазовая постоянная.
3. Расчет входных сопротивлений.
Входное сопротивление ЧП имеет смысл только при наличии нагрузки. Если сопротивление нагрузки равно характеристическому сопротивлению ЧП, то такой режим работы ЧП называется согласованным, если не равно, то – несогласованным.
Если входное сопротивление рассчитывается со стороны зажимов 1 – 1, то оно может быть найдено по формуле
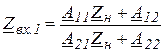 , (4.1)
, (4.1)
если со стороны зажимов 2 – 2, то – по формуле
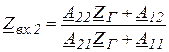 . (4.2)
. (4.2)
В согласованном режиме, т.е. когда ![]() Ом, а
Ом, а ![]()
![]() , получим:
, получим:
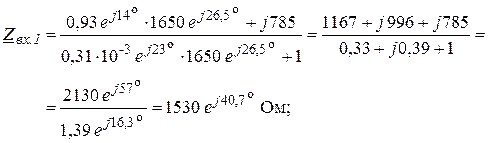
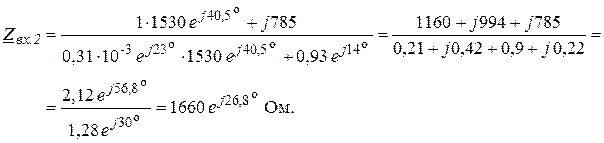
В режиме несогласованного включения ЧП, когда ![]() = 3300 Ом, а
= 3300 Ом, а ![]() = 3060 Ом, получим:
= 3060 Ом, получим:
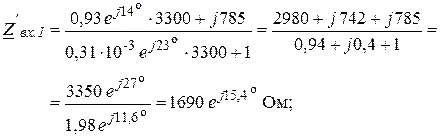
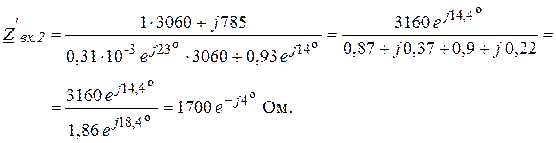
Анализ полученных результатов подтверждает известное положение теории о том, что входное сопротивление согласованно нагруженного ЧП равно его характеристическому сопротивлению.
4. Анализ прохождения сигнала в системе: источник сигнала – ЧП – нагрузка.
С этой целью в схеме, приведенной на рис. 4.1, необходимо рассчитать значения напряжений ![]() ,
, ![]() и токов
и токов ![]() и
и ![]() . Эти величины легко могут найдены с помощью уравнений передачи ЧП для А
-параметров:
. Эти величины легко могут найдены с помощью уравнений передачи ЧП для А
-параметров:
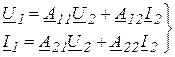 . (4.3)
. (4.3)
Предварительно находится напряжение
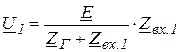 . (4.4)
. (4.4)
Тогда из уравнения ![]() определяем
определяем
 (4.5)
(4.5)
Ток ![]() может быть найден либо по (4.3), либо по формуле
может быть найден либо по (4.3), либо по формуле
|
Рис. 4.5 |
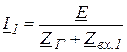 . (4.6)
. (4.6)
Роль ЧП в схеме оценивается через его рабочее ослабление
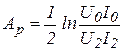 , (4.7)
, (4.7)
где ![]() , и
, и ![]() – напряжение и ток на согласованной нагрузке источника сигнала без ЧП (рис. 4.5).
– напряжение и ток на согласованной нагрузке источника сигнала без ЧП (рис. 4.5).
Рассчитаем перечисленные величины в случае, когда ![]() , а
, а ![]() . Учтем, что
. Учтем, что ![]() .
.
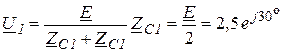 ;
;
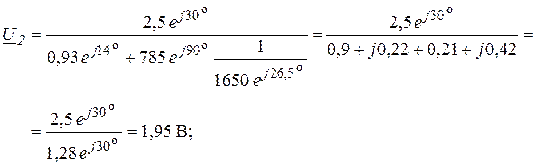
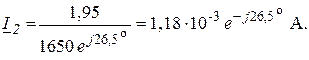
Ток ![]() , рассчитанный по (4.6)
, рассчитанный по (4.6)
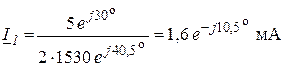 ,
,
совпадает с результатом расчета ![]() по (4.3).
по (4.3).
Значения ![]() и
и ![]() в схеме на рис. 4.5 находятся при
в схеме на рис. 4.5 находятся при ![]() . Очевидно, что в этом случае
. Очевидно, что в этом случае
![]() ,
,
а 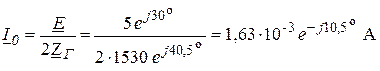 .
.
Тогда
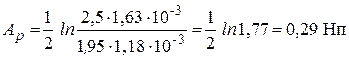 .
.
Теже величины в случае несогласованного включения ЧП, т.е. при ![]() = 3300 Ом,
= 3300 Ом, ![]() = 3060 Ом и
= 3060 Ом и ![]() Ом, будут иметь значения:
Ом, будут иметь значения:
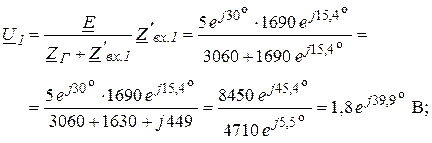
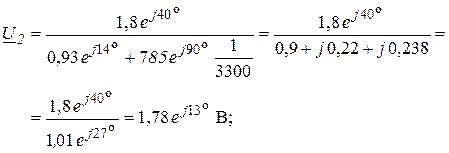
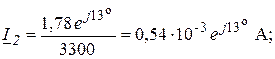
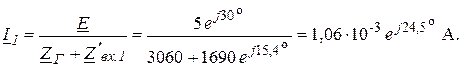
При расчете рабочего ослабления в несогласованном режиме в схеме на рис. 4.5 необходимо принять ![]() = 3060 Ом. В этом случае напряжение
= 3060 Ом. В этом случае напряжение ![]() не изменится и вновь будет равно
не изменится и вновь будет равно ![]() , а ток
, а ток ![]() изменится:
изменится:
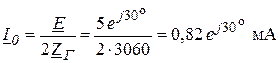 .
.
Рабочее ослабление согласно (4.7) будет:
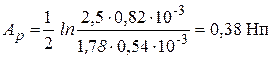 .
.
Анализ расчетов показывает, что рабочее ослабление ЧП при несогласованном включении 0,38 Hn больше, чем при согласованном включении 0,29 Hп, что и следовало ожидать. Кроме того рабочее ослабление в режиме согласованного включения ЧП равно характеристическому ослаблению ЧП, рассчитанному в п. 2.
5. Расчет комплексной передаточной функции.
Согласно рис. 4.1 комплексная передаточная функция ЧП по напряжению ![]() . Используя первое уравнение из системы (4.3), легко получить, что
. Используя первое уравнение из системы (4.3), легко получить, что
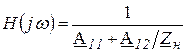 .
.
В режиме холостого хода, т.е. при ![]() и при частоте
и при частоте ![]() = 5 кГц
= 5 кГц
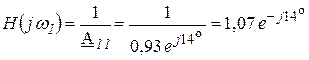 .
.
Модуль передаточной функции ![]() оказался больше единицы несмотря на то, что ЧП является пассивным. Но, т.к. в схеме ЧП имеются индуктивность и емкость, то возникают резонансные явления, которые и приводят к увеличению выходного напряжения по сравнению с входным.
оказался больше единицы несмотря на то, что ЧП является пассивным. Но, т.к. в схеме ЧП имеются индуктивность и емкость, то возникают резонансные явления, которые и приводят к увеличению выходного напряжения по сравнению с входным.
Если учитываются нагрузки ЧП, то вводится понятие рабочей передаточной функции:
![]() .
.
Обычно рассчитывается модуль рабочей передаточной функции:
![]() .
.
В режиме согласованного включения ЧП
![]() .
.
В режиме несогласованного включения
![]() .
.
Задача 4.2
Исследуется режим в длинной линии (рис. 4.5), на входе и выходе которой подключена одинаковая нагрузка ![]() .
.
Выпишите согласно Вашему варианту параметры задачи (табл. 7).
Определив номер задания Вашего варианта (табл. 1) с помощью таблицы 8 найдите и выпишите, что задано и что требуется рассчитать.
|
Рис. 4.5 |
Найдите величину нагрузки ![]() , при которой в линии будут отсутствовать отраженные волна. Чему равен КБВ при найденном значении
, при которой в линии будут отсутствовать отраженные волна. Чему равен КБВ при найденном значении ![]() ? Расчет задачи выполняйте в предположении, что
? Расчет задачи выполняйте в предположении, что ![]() совпадает с найденным значением
совпадает с найденным значением ![]() .
.
Таблица 7
| Варианты |
|
|
l , км |
х , км |
| 00 – 09 |
70 |
0,1 + j 0,3 |
5 |
2 |
| 10 – 19 |
35 |
0,1 + j 0,5 |
7 |
2 |
| 20 – 29 |
45 |
0,05 + j 0,1 |
10 |
3 |
| 30 – 39 |
50 |
0,04 + j 0,15 |
15 |
11 |
| 40 – 49 |
75 |
0,06 + j 0,12 |
20 |
13 |
| 50 – 59 |
130 |
0,02 + j 0,06 |
25 |
18 |
| 60 – 69 |
150 |
0,03 + j 0,08 |
30 |
15 |
| 70 – 79 |
180 |
0,01 + j 0,05 |
40 |
22 |
| 80 – 89 |
200 |
0,02 + j 0,07 |
50 |
19 |
| 90 – 99 |
250 |
0,01 + j 0,05 |
35 |
28 |
Таблица 8
| Номер задания |
Что задано |
Что найти |
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
Типовая задача Т4.2
В согласованно нагруженной на входе и выходе длинной линии (рис. 4.5) с параметрами:
волновое сопротивление – ![]() Ом,
Ом,
коэффициент распространения – ![]() 1/км,
1/км,
рассчитать напряжение ![]() на расстоянии x
= 6 км от начала линии, если э.д.с.
на расстоянии x
= 6 км от начала линии, если э.д.с.
![]() мВ.
мВ.
Решение
Запишем комплексное значение амплитуды э.д.с.:
![]() .
.
|
Рис. 4.6 |
Рассмотрим схему замещения входного сосредоточенного узла длинной линии (рис. 4.6) при условии, что ![]() .
.
По закону Ома для одноконтурной схемы замещения рассчитываем комплексную амплитуду входного тока линии:
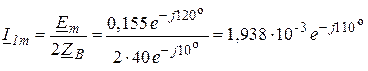 А.
А.
Ток на расстоянии х определится по уравнению падающей бегущей волны:
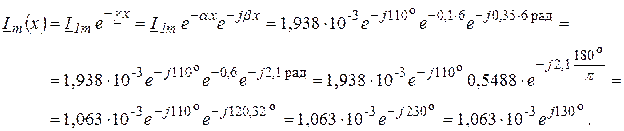
Здесь последнее значение угла получено после сложения с углом 360° (поворот вектора на 360° не изменил физическое значение угла, но позволил получить меньшее по модулю значение аргумента комплексного выражения тока).
Комплексную амплитуду искомого напряжения находим по закону Ома для бегущей волны:
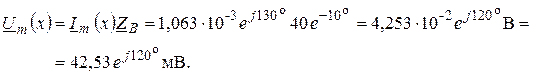
Поэтому искомая зависимость мгновенного значения напряжения на заданном расстоянии х = 6 км имеет вид:
![]()
Оглавление
Стр.
Общие замечания .......................................................................................... 3
Список литературы ...................................................................................... 3
Разделы, изучаемые в пятом семестре ......................................................... 5
Вопросы для самоконтроля ......................................................................... 13
Разделы, изучаемые в шестом семестре ...................................................... 14
Вопросы для самоконтроля ......................................................................... 19
Контрольные задания и порядок их выполнения ....................................... 20
Выбор варианта ............................................................................................ 20
Требования к оформлению контрольных работ ......................................... 20
Контрольная работа № 3 ............................................................................. 22
Задача 3.1 ...................................................................................................... 22
Типовая задача Т3.1 ..................................................................................... 24
Задача 3.2 ...................................................................................................... 30
Типовая задача Т3.2 ..................................................................................... 32
Контрольная работа № 4 ............................................................................. 39
Задача 4.1 ...................................................................................................... 39
Типовая задача Т4.1 ..................................................................................... 41
Задача 4.2 ...................................................................................................... 47
Типовая задача Т4.2 ..................................................................................... 48
св. план 1999, поз.
Бакалов Валерий Пантелеевич
Рожков Виктор Михайлович
Методические указания и контрольные задания № 3 и № 4
по курсу
ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
для студентов заочного факультета
3 курса
Редактор
Корректор
Компьютерный набор и верстка: Гусельникова Н.М.
Лицензия № 020472, октябрь 1992 г. Подписано в печать
Формат бумаги 62х84 1/16
Бумага писчая № 1. Уч. изд. л 3. Тираж 250 экз.
Заказ №
Типография СибГУТИ, 630102. г. Новосибирск, ул. Кирова, 86