Методические указания к выполнению лабораторных работ по дисциплине теория электрической связи для студентов специальности

СОДЕРЖАНИЕ: Методические указания предназначены для студентов дневной формы обучения по специальности «Телекоммуникационные системы и сети»

МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«Кафедра автоматика и телекоммуникации»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению лабораторных работ по дисциплине

ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ

для студентов специальности

7.0924012 «Телекоммуникационные системы и сети»

Часть 1

Донецк - 2004.

Методические указания к лабораторным работам по дисциплине «Теория электрической связи» для студентов специальности ТКС/Воронцов А.Г. – Донецк, ДонГТУ, 2004. – 57с.

Методические указания к выполнению лабораторных работ включают в себя описание лабораторных работ, рекомендуемую литературу, перечень контрольных вопросов, дополнительные задания.

Методические указания предназначены для студентов дневной формы обучения по специальности «Телекоммуникационные системы и сети».

Составитель: Воронцов А. Г.

Утверждены на заседании кафедры

«Автоматика и телекоммуникации»,

протокол № __от__________2004 г.

ЛАБОРАТОРНАЯ РАБОТА №1

ЦИФРОВОЙ ЧАСТОТНЫЙ АНАЛИЗ ПОЛИГАРМОНИЧЕСКИХ СИГНАЛОВ

Цель работы: Изучить частотный анализ полигармонических сигналов цифровыми средствами.

Задачи работы:

1. Ознакомиться с методами и техникой оценивания частот и относительных амплитуд компонент полигармонических сигналов.

2. Исследовать явление «утечки» при цифровом частотном анализе и его влияние на достоверность получаемых результатов.

3. Исследовать влияние помех на результаты оценки параметров полигармонических сигналов.

4. Изучить методы повышения точности оценивания частоты и амплитуды гармонических компонент сигнала при частотном анализе.

ВВЕДЕНИЕ

Цифровые средства широко применяются в технике связи для обработки сигналов и оценки параметров последних. Их применение позволяет существенно повысить качество работы систем. Однако применение цифровых методов имеют некоторые особенности в сравнении с традиционными аналоговыми методами, которые необходимо знать для получения достоверных результатов и правильной их интерпретации. В частности, следует правильно и обосновано задавать длительность исследуемой реализации, параметры временной дискретизации, динамический диапазон, вид используемой шкалы для представления результатов. Кроме того, следует принимать во внимание некоторые специфические эффекты, имеющие место в цифровых системах связанных с обработкой выборок конечного объема, ограниченным динамическим диапазоном, влиянием шумов.

Данная работа направлена на изучение указанных вопросов средствами моделирующего пакета System View.

ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ

Во многих случаях электрический сигнал удобно рассматривать как сумму ограниченного числа гармонических компонент

,

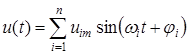где - амплитуда, -частота и - фаза i - й компоненты.

Для непериодических сигналов такое представление является приближенным, однако, за счет выбора достаточно большого значения n , как правило, можно получить удовлетворительную степень приближения.

Гармонические компоненты в составе сигнала могут иметь близкие частоты и значительное отличие в амплитудах. Кроме того, длительность реализации исследуемого сигнала может оказаться недостаточной для получения надежных оценок параметров. Слишком же большая длительность потребует большого объема памяти ЭВМ и времени на обработку. Рациональные задания объема выборки, программных инструментов обработки реализаций, средств представления и визуализации результатов, а так же настроек соответствующих программ позволяет наиболее эффективно решить задачу частотного анализа.

В данной лабораторной работе исследуемым сигналом является трехкомпонентный сигнал

. (1)

Выражение (1) описывает неограниченный по длительности процесс. По указанному выражению может быть построен идеальный (теоретический) спектр амплитуд. Реально же, мы имеем возможность наблюдать и исследовать только процессы ограниченной длительности. Если на основе таких ограниченных реализаций производится спектральное оценивание, то получаемый оценочный спектр может иметь значительные отличия от идеального. Искажения результатов возникают вследствие явления «утечки» – растекания энергии сосредоточенных спектральных компонент в прилегающих к ним частотных областях. Утечка снижает разрешающую способность спектрального анализа, что приводит к невозможности выделить близкие по частоте компоненты. Другим негативным последствием утечки является эффект «маскировки» компонент малого уровня, присутствующих в составе сигнала. Явление утечки можно существенно уменьшить, если обеспечить относительно плавное нарастание и убывание уровня исследуемого сигнала в начале и в конце реализации. Для этого используются временные окна – унимодальные функции времени, определенные на том же временном интервале, что и исследуемая реализация и изменяющиеся в интервале (0, 1). Примерами таких окон могут служить окно Барлетта (в виде равнобедренного треугольника), окно Ханнинга (в виде косинусоиды, взятой с обратным знаком и смещенной по оси ординат на 1) и др. Применение временного окна к сигналу (взвешивание сигнала) состоит в умножении ограниченной реализации на функцию временного окна. Спектр взвешенного сигнала, конечно же, отличается от идеального спектра. Однако, он может иметь лучшие характеристики спектрального оценивания, в частности, меньший маскирующий эффект в ближней или дальней зоне по отношению к порождающей его гармонической компоненте. Это позволяет обнаруживать в составе сигнала составляющие малого уровня, обеспечить более глубокий его анализ. Уменьшая влияние маскирующего эффекта явления утечки, взвешивающие окна могут ухудшить другие характеристики спектрального оценивания, в частности, разрешение по частоте. Поэтому, при исследовании реальных сигналов часто приходится подбирать подходящее окно, обеспечивающее наилучшую оценку того или иного параметра спектра сложного сигнала.

В рамках данной лабораторной работы, эффективность используемых окон определяется путем сравнения спектральных оценок, получаемых с их применением, с идеальным спектром исследуемого сигнала. В качестве количественных мер эффективности используются превышение уровня оцениваемой (слабой) гармонической компоненты над помехой, вызванной утечкой, а также разрешающая способность, определяемая как минимальное расстояние по частоте между компонентами, при котором они еще различимы как таковые.

Явление утечки и применение взвешивающих окон не позволяют осуществлять непосредственную оценку абсолютного уровня амплитуд гармонических компонент исследуемого сигнала, однако позволяют получать относительные оценки уровня компонент в составе сигнала. Абсолютные значения составляющих могут быть найдены, если в состав исследуемого сигнала ввести эталонную (калибровочную) гармоническую компоненту известной амплитуды и на основе оценки ее уровня в составе спектра исследуемого сигнала произвести расчет амплитуд остальных компонент спектра.

В ходе выполнения лабораторной работы оценивание уровня спектральных компонент целесообразно осуществлять через спектр мощности сигнала (тока или напряжения) выделяемой на сопротивлении в 1 Ом. Получаемые в этом случае значения оценок уровня не зависят от того, какой физической величиной (током или напряжением) представлен электрический сигнал. Напомним, что

, , (2)

где P- мощность; U , I – действующие (или среднеквадратическое) значения напряжения и тока; R – сопротивление цепи.

Для обеспечения возможности представления на одном графике как малых, так и больших уровней сигналов одновременно необходимо использовать нелинейный (логарифмический) масштаб. Соответствующие оси координат в таком случае аннотируются в децибелах. Напомним, что

; (3)

; (4)

. (5)

Здесь - некоторый эталонный уровень тока, напряжения или мощности.

Следует иметь ввиду, что в используемой в данной и последующей работах цифровой моделирующей системе непрерывные зависимости представляются дискретно своими отсчетами, поэтому качество выводимых на экран графиков существенно зависит от количества точек, отображающих эти отсчеты. При недостаточном количестве точек представляемая на экране картина может не соответствовать действительной из-за недостатка информации для ее восстановления по имеющимся отсчетам.

По ходу работы некоторые параметры исследуемого сигнала (1) могут изменяться, в его состав может быть введена дополнительная компонента в виде Гауссова случайного процесса (помехи).

Задачи данной лабораторной работы реализуются путем выбора подходящих взвешивающих окон, изменения длительности реализации, а так же параметров визуализации, при которых обеспечиваются наилучшие результаты оценки.

ХОД ВЫПОЛНЕНИЯ РАБОТЫ

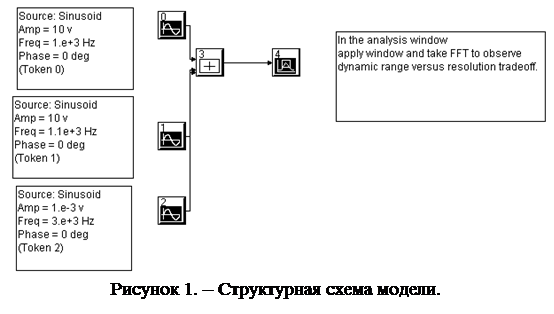
1.Загрузить исполняющий файл dsp_wind.svu (рис.1). Записать параметры модулей модели, параметры системного времени. Сравнить эти параметры с параметрами трехкомпонентного полигармонического сигнала (1).

2.Запустить модель на цикл моделирования. Получить графики выходного сигнала (Sink4) и его спектра. Используя перемещаемый «мышью» курсор и поле индикации его координат (область правого верхнего угла окна анализа), оценить характерные величины представления сигналов в анализирующих окнах (минимальное и максимальное значение огибающей амплитуд, период изменения огибающей, период частотного заполнения). Сравнить полученные результаты с параметрами идеального сигнала. Воспользовавшись «калькулятором» пакета System View получить спектр мощности исследуемого сигнала, выделяемой на резисторе в 1 Ом. Отметить влияние «утечки» энергии одних спектральных компонент сигнала на соседние и ее влияние на достоверность результатов оценивания относительной амплитуды и частоты. Сделать выводы относительно возможности и достоверности оценки параметров исследуемого сигнала.

3.Подвергнуть временную реализацию сигнала «взвешиванию» (windowing) с использованием стандартных окон Барлетта (Barlett), Ханнинга (Hanning), Эланикс (Elanix). Для каждого случая получить спектр «взвешенного» сигнала. Произвести оценку параметров амплитуды и частоты каждой из компонент сигнала для каждого случая. Выполнить эскизы графиков спектров с указанием полученных оценок. Сравнить полученные результаты с параметрами идеального сигнала. Сделать выводы относительно возможности и достоверности оценки параметров при использовании «взвешивающих» временных окон.

4.Ввести в состав сигнала аддитивный Гауссов шум, путем дополнения источников еще одним – источником Гауссова шума с математическим ожиданием (mean) равным 0 и среднеквадратическим отклонением (Std Deviation) равным 0,0003В. Получить график спектра с использованием окна Ханнинга. Получить оценки частоты и амплитуды для каждой спектральной компоненты. Так как помеха носит случайный характер, следует повторить цикл моделирования и получения оценок сигнала многократно (не менее 5-ти раз), а искомые оценки находить как средние величины считываемых значений оцениваемых параметров для каждого цикла моделирования. Повторить вышеприведенную последовательность получения оценок параметра сигнала для значений среднеквадратического отклонения 0,001В и 0,003В. Данные расчетов свести в таблицу. Привести график спектра сигнала для второго цикла моделирования. Сделать выводы относительно влияния помех на возможность и достоверность оценок параметров сигнала.

5.Восстановить исходную структуру и параметры модели (См. п.1). Вызвать панель настроек системного времени и установить число циклов моделирования (№ of System Loops) равным 10. Выполнить пункт 2 данного «Хода выполнения работы» при новых настройках. Выполнить пункт 3 данного «Хода выполнения работы» (использовать только окно Эланикс). Сделать выводы относительно влияния длины реализации и на достоверность оценок. Отметить влияние взвешивающего окна на полученные результаты в сравнении с п.2.

ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ

1. Изучить материал лабораторной работы по методическим указаниям и рекомендованной литературе.

2. В черновой тетради подготовки к лабораторным работам привести:

- схему исследуемой модели;

- график идеального спектра амплитуд сигнала (1);

- спектр мощности сигнала (1), выделяемой на резисторе в 1 Ом;

- расчет амплитуды гармонических компонент сигнала, уровень которых составляет 40 дБм и –10 дБм.

3. Ответить на вопросы контрольного задания.

СОДЕРЖАНИЕ ОТЧЕТА

1. Наименование работы, ее цель и задачи.

2. Структура модели, ее параметры, параметры системного времени.

3. Эскизы графиков сигналов, их спектров с указанием полученных оценок параметров, а так же выводы в соответствии с пунктами 2…5 «Хода выполнения работы».

4. Выводы по работе в целом.

ЛИТЕРАТУРА

1. Харкевич А.А., Спектр и анализ. Стр. 13…19, 42…46.

2. Марпл – мл. С.Л., Цифровой спектральный анализ и его приложения. Стр. 164…184.

КОНТРОЛЬНЫЕ ВОПОСЫ

1. К какому классу сигналов должен быть отнесен исследуемый в данной работе сигнал на этапе задания, различных этапах обработки, на этапе выдачи результатов обработки?

2. Как можно оценить абсолютное значение амплитуды спектральной компоненты сигнала по его спектру амплитуд, представленному в логарифмическом масштабе?

3. Как влияет увеличение объема выборки на точность оценки частоты гармонической компоненты сложного сигнала?

4. Как влияет использование «взвешивающих» окон на точность частотных оценок? Ответ сформулировать применительно как для «сильных», так и для «слабых» компонент, входящих в состав сигнала.

5. В каких случаях целесообразно использовать логарифмический, а в каких линейный масштаб при оценивании сложного, полигармонического сигнала?

ЛАБОРАТОРНАЯ РАБОТА №2

СИСТЕМЫ СВЯЗИ С ЧАСТОТНЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ

Цель работы: Изучить принципы построения систем связи с частотным разделением каналов.

Задачи работы:

1. Изучить структуру и функции основных узлов системы с частотным разделением каналов для передачи непрерывных и дискретных сообщений.

2. Изучить влияние спектральных характеристик передаваемых сигналов на качество их разделения и восстановления переданного сообщения на приемной стороне.

3. Исследовать влияние помех на качество работы системы связи при частотном разделении сигналов.

ВВЕДЕНИЕ.

Одна из важнейших задач решаемых в телекоммуникационных системах – задача разделения сигналов передаваемых по одной физической линии связи совместно. Разделение осуществляется по заранее известным и неизменным признакам, индивидуальным для каждого из разделяемых сигналов. Наиболее часто при создании систем связи применяется разделение сигналов по частотному признаку. На основе частотного разделения реализуются системы многоканальной телефонной и радиосвязи, системы спутниковой связи, системы радиовещания и телевидения. Такие системы содержат в своем составе группу передатчиков и приемников взаимодействующих через общую среду распространения сигналов (кабельная линия, околоземное и космическое пространство – «эфир» и т.д.). В простейшем случае каждая пара передатчик – приемник и среда, связывающая их, составляют отдельный канал. Для обеспечения возможности одновременной передачи сообщений по всем каналам необходимо выполнить условия независимости их работы, исключения влияния друг на друга, что и составляет задачу разделения сигналов и соответствующих каналов связи. Основой частотного разделения каналов являются следующие положения:

- Каждый из передатчиков формирует и выдает в среду распространения сигналы, имеющие спектры не перекрывающиеся со спектрами других передатчиков;

- Каждый из приемников имеет средства выделения спектров сигналов только нужного передатчика и подавления спектров других;

- Среда распространения сигналов обладает линейными свойствами.

Данная работа направлена на изучение реализации этих положений на примере простейшей двухканальной системы связи, моделируемой средствами пакета System View.

ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ.

Объектом исследования в данной работе является модель двухканальной системы связи. В работе предусматривается исследование двух версий системы и, соответственно, двух версий модели - первая, для передачи непрерывных сообщений (См. рис.1) и вторая, - для передачи дискретных (См. рис.2). Сообщения для первой модели представлены гармоническими колебаниями различных частот. Физически это может соответствовать передаче по каждому из каналов звуковых сигналов, отображающих звучание нот различных тональностей. Для второй модели сообщения представлены импульсными последовательностями с различной длительностью импульсов. Физически это может отображать передачу последовательности «точек» телеграфной азбуки по одному каналу и «тире» - по другому.

В состав обеих моделей системы входят модули передатчиков, представленных на левой части рисунков и приемников – на правой части. Среда распространения – линия связи, представлена сумматором и источником Гауссова шума, в центральной части рисунка.

Передатчик представлен модулятором (модули 2,19,23 для первого канала и модули 2,24 для второго), осуществляющим перенос передаваемого сообщения (генерируется модулями 7 и 8 для соответствующих каналов) на несущее гармоническое колебание (генерируется модулями 0 и 1) путем управления его амплитудой.

Приемник каждого канала представлен фильтром (модули 6 и 9), пропускающим только частотные компоненты своего передатчика, и детектором огибающей (модули 14, 16 и 15, 17). В свою очередь каждый детектор содержит нелинейный элемент (двухполупериодный выпрямитель) и фильтр, пропускающий частотные компоненты восстанавливаемого в детекторе сообщения.

Следует иметь ввиду, что первое условие разделения сигналов, упомянутое во Введении, в реальных системах выполняется с известной степенью приближения. Спектры реальных сигналов в той или иной степени перекрываются. Это можно объяснить своеобразной «утечкой», так как реальный сигнал всегда изменяется и, следовательно, в нем нельзя выделить протяженный стационарный участок. В силу указанного энергия реального сигнала всегда распределена в некоторой частотной области, сгруппированной в окрестности частоты несущего колебания. По мере удаления от этой области энергия частотных компонент сигнала уменьшается. Количественной мерой ширины полосы частот, занимаемой сигналом, может служить так называемая существенная полоса частот (ширина спектра), на границах которой уровень энергии (мощности) частотных компонент составляет заданную, достаточно малую часть (сотую, тысячную и т.п) энергии наиболее мощных компонент центральной части спектра.

Упомянутое выше явление утечки приводит к тому, что некоторая часть энергии передатчика попадает в полосу частот сигнала «не своего» приемника. Таким образом, соседние каналы создают помехи друг другу. Что бы такие помехи были несущественными, необходимо чтобы уровень просачивающейся помехи был мал в сравнении с полезным сигналом. Количественно это оценивается степенью перекрытия спектров смежных каналов, определяемой как отношение мощности существенной части полезного сигнала, сконцентрированной, как правило, в центральной части его спектра, к мощности смеси сигнала и помехи на границе полосы пропускания фильтра приемника.

Задачи данной работы реализуются путем анализа сигналов в различных точках системы, их сопоставления и оценки, как во временной, так и в частотной областях.

ХОД ВЫПОЛНЕНИЯ РАБОТЫ.

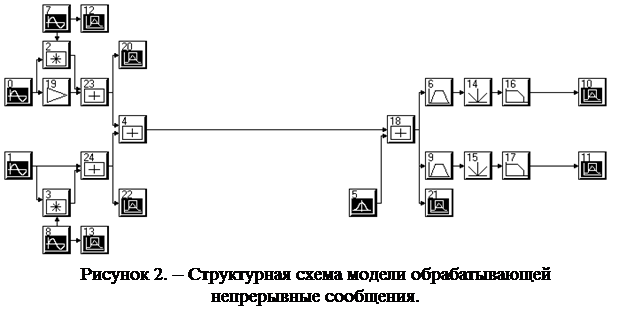1.Загрузить исполняющий файл chrch..svu (Рис.2). Зарисовать структуру модели, записать параметры ее модулей и параметры системного времени.

2.Запустить модель на цикл моделирования. Получить графики исходных сообщений. (Sink 12,13) и оценить параметры сигналов, которые их представляют (Sink 20,22) (максимальное и минимальное значение уровня огибающей, ее период и частота, период и частота гармонического заполнения).

3.Получить спектры модулированных сигналов на выходе передатчиков. Для получения детальной картины спектра в области несущей частоты следует использовать изменение масштаба по оси абсцисс. Оценить ширину спектра каждого сигнала на уровне –20дБ относительно уровня несущего колебания.

4.Получить график сигнала в линии связи (Sink21) и спектр этого сигнала. Оценить степень перекрытия спектров сигналов различных передатчиков. Сделать выводы о возможности разделения сигналов, если допустимый уровень просачивания не должен превышать –20дБ в сравнении с энергией (мощностью) существенной части спектра полезного сигнала. Оценить возможности сближения частот несущих колебаний обоих передатчиков без нарушения условий частотного разделения. Обосновать значения несущих колебаний для случая допустимого перекрытия спектров на уровне –-20дБ.

5.Получить графики принятых сообщений на выходах приемников (Sink10,11) и сравнить их с передаваемыми (Sink12,13). Оценить время распространения сообщений по каналу связи. В отчете достаточно привести один из полученных графиков.

6.Установить среднеквадратическое отклонение Гауссова шума равным 0,1В и запустить модель на цикл моделирования. Получить график сигнала в линии связи (Sink21) и спектр этого сигнала. Выполнить п.5 “Хода выполнения работы”. Сделать вывод о возможности восстановления переданного сообщения.

7.Выполнить п.6 “Хода выполнения работы” для среднеквадратического отклонения Гауссова шума равного 0,3В и 1В. Сделать вывод о возможности восстановления переданного сообщения. Графики наблюдаемых сигналов для этого случая в отчете не приводить.

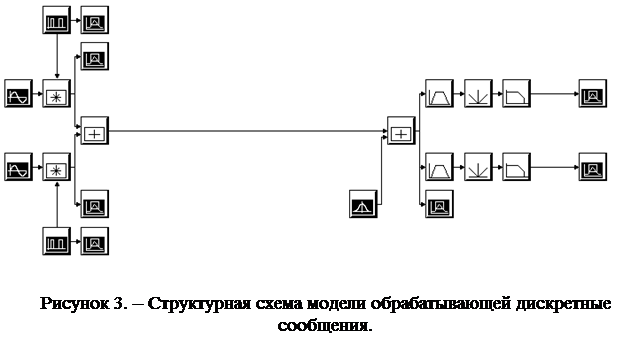8.Выполнить пп.1…8 “Хода выполнения работы” для второй модели системы, обрабатывающей дискретные сообщения. Исполняющий файл chrch1.svu (Рис.3).

ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ

3. Изучить материал лабораторной работы по методическим указаниям, конспекту лекций и рекомендованной литературе.

4. В черновой тетради подготовки к лабораторным работам привести:

- схему исследуемых модели;

- график идеального спектра амплитуд сигнала в линии связи, когда модуляция отсутствует (сигналы, отображающие передаваемые сообщения, считать равными нулю), если несущие колебания описываются выражениями

и ;

- идеальный спектр мощности несущих колебаний, выделяемой на резисторе в 1 Ом;

- определить относительный уровень несущих колебаний в децибелах

3. Ответить на вопросы контрольного задания.

СОДЕРЖАНИЕ ОТЧЕТА

1. Наименование работы, ее цель и задачи.

2. Структурные схемы моделей, параметры их модулей, параметры системного времени.

3. Эскизы графиков сигналов, их спектров с указанием полученных оценок параметров, а так же выводы в соответствии с пунктами 1…8 «Хода выполнения работы».

4. Выводы по лабораторной работе в целом. В общих выводах сравнить систему передачи непрерывных и дискретных сообщений, указать на их особенности, обнаруженные в ходе лабораторных исследований.

ЛИТЕРАТУРА.

1. Кловский Д.Д. Теория передачи сигналов. Стр. 314…319.

2.Теория электрической связи/ Под. Ред. Д.Д. Кловского. М. Радио и связь,1999. Стр. 10-24, 353-355.

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Каким обязательным требованиям должны удовлетворять параметры канальных модулей и сигналов в системе с частотным разделением?

2. Одинаковы ли условия работы различных каналов системы? Ответ обосновать, сравнивая работу высокочастотных и низкочастотных каналов.

3. Как влияет увеличение числа одновременно работающих каналов на работу линейного оборудования? Ответ обосновать, принимая во внимание, что в составе линейного общего для всех каналов оборудования могут быть усилители, преобразователи и другие активные устройства.

4. Чем качественно отличается работа системы с частотным разделением при передаче непрерывных сообщений и дискретных сообщений?

5. Как влияют помехи на выполнение системой функций разделения сигналов?

ЛАБОРАТОРНАЯ РАБОТА №3

СИСТЕМА СВЯЗИ С ВРЕМЕННЫМ РАЗДЕЛЕНИЕМ КАНАЛОВ.

Цель работы: Изучить принципы построения систем связи с временным разделением каналов.

Задачи работы:

1. Изучить структуру и функции основных узлов системы с временным разделением каналов для передачи непрерывных сообщений.

2. Изучить основные положения временного разделения каналов связи и их реализацию в системах.

3. Исследовать принципы временной дискретизации сигналов, определяемые теоремой В.А.Котельникова.

ВВЕДЕНИЕ.

Временное разделение каналов применяется достаточно часто при создании систем связи. На основе временного разделения реализуются системы многоканальной телефонной связи, системы спутниковой связи и телевидения. Для обеспечения возможности одновременной работы нескольких каналов по одной линии связи необходимо выполнить условия независимости их работы, исключения влияния друг на друга, что составляет задачу разделения каналов. Основой временного разделения каналов являются следующие положения:

- Каждый из передатчиков формирует и выдает в среду распространения сигналы только в отведенные для него интервалы времени не перекрывающиеся с интервалами, отведенными для других передатчиков;

- Каждый из приемников имеет средства выделения интервалов передачи, а, следовательно, и сигналов только нужного передатчика и подавления сигналов других. (Для этого в составе системы должны быть средства, обеспечивающие синхронную работу передатчиков и приемников, поочередно предоставляющие среду распространения в их распоряжение и средства восстановления сообщений из квантованных по времени сигналов - интерполирующие фильтры);

-Дискретизация сигналов представляющих сообщения осуществляется с соблюдением требований теоремы В.А.Котельникова;

-Среда распространения сигналов обладает достаточной широкополосностью и линейностью с тем, что бы передаваемые импульсные сигналы не были искажены.

Данная работа направлена на изучение реализации этих положений на примере простейшей системы связи, моделируемой средствами пакета System View.

ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ.

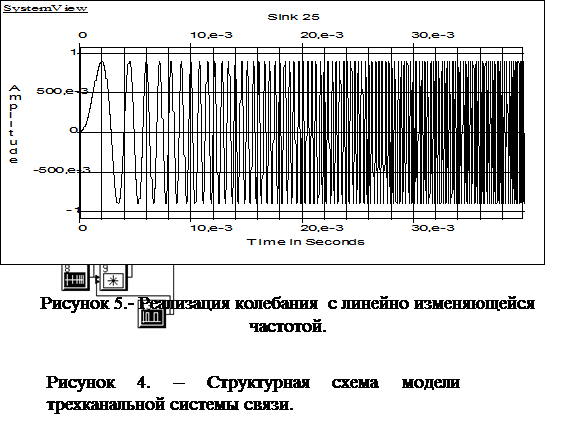Объектом исследования в данной работе является модель трехканальной системы связи (См. рис.4). Сообщения в модели представлены гармоническим колебанием, частота которого изменяется линейно в интервале (См. рис.5).

В первом приближении можно считать, что спектр такого колебания сосредоточен в полосе .

Необходимой процедурой обработки сигналов при временном разделении является временная дискретизация, в результате которой непрерывная временная реализация заменяется отсчетами, следующими с заданным интервалом. Для восстановления исходной формы непрерывного колебания по дискретным отсчетам необходимо, что бы на периоде его изменения было сделано достаточно большое количество отсчетов, т.е. интервал дискретизации достаточно мал. Условия, при которых возможно восстановление непрерывного колебания, определяются теоремой Котельникова. Наименьшее число отчетов на периоде требуется для восстановления гармонического колебания, и оно равно двум.

Дискретные отсчеты, формируемые передатчиками, последовательно перемежаясь передаются в линию связи и таким образом формируется новая результирующая (линейная) последовательность. На приемной стороне приемники воспринимают только «свои» отсчеты. Это обеспечивается синхронной и синфазной работой ключей дискретизаторов передатчиков и соответствующих ключей – клапанов приемников. В качестве таких ключей используются перемножители. На один вход перемножителя поступает обрабатываемый сигнал, на второй- сигнал от импульсного генератора тактирования. Импульсы тактирования могут принимать только два уровня – единичный и нулевой.

Модули передатчиков, входящие в состав модели системы, представлены в левой части рисунка и приемников – на правой части. Работа приемников и передатчиков синхронизирована общими для каждой пары приемник - передатчик генераторами импульсов тактирования и управляемых ими ключами-коммутаторами на передающей и приемной сторонах. Тактовые генераторы работают так же синхронно и синфазно. Фазовый сдвиг между импульсами формируемых ими последовательностей составляет 120⁰ .

Среда распространения–линия связи, представлена сумматором сигналов в центральной части рисунка. Если линия связи вносит запаздывание или искажает форму импульсных сигналов (например, затягивая их на интервалы смежных отсчетов) работа системы связи ухудшается и может быть нарушена полностью.

Задачи данной лабораторной работы реализуются путем анализа сигналов в различных точках системы, их сопоставления и оценки как во временной, так и в частотной областях.

ХОД ВЫПОЛНЕНИЯ РАБОТЫ.

1.Загрузить исполняющий файл time_rch..svu модели. Записать параметры ее модулей, параметры системного времени.

2.Запустить модель на цикл моделирования. Получить графики исходных сообщений. (Sink 20,21,22) и оценить их параметры (амплитуды и длительности).

3.Получить графики принятых сообщений на выходах приемников (Sink 5,18,19) и сравнить их с передаваемыми (Sink20,21,22).Сделать выводы относительно возможности восстановления передаваемых сообщений на приемной стороне.

4.Получить графики сигналов синхронизации (Выходы модулей 2,12,13) и оценить их параметры. Для этого следует установить на выходах указанных модулей модули регистрации сигналов и повторно запустить модель на цикл моделирования. Соответствуют ли эти сигналы условиям временного разделения каналов? При выполнении пп.4,5 с целью улучшения разрешения следует использовать изменение масштаба времени, рекомендуемый диапазон представления сигнала 0…0,005с.

5.Получить график сигнала в линии связи и его спектр (Sink11). Оценить ширину спектра сигнала на уровне –20дБ относительно его максимального уровня. Оценить перекрытие сигналов различных передатчиков во времени.

6.Сделать фазу следования импульсов генератора второго передатчика (Модуль 12) совпадающей с фазой генератора первого (Модуль 2). Запустить модель на цикл моделирования и выполнить п.3“Хода выполнения работы”. Возможно ли восстановление передаваемых сообщений в этом случае? Объяснить причину наблюдаемых явлений.

7.Восстановить исходные значения фазы тактового генератора 2. Изменить частоту следования импульсов всех тактовых генераторов (Модули 2,12,13) и сделать ее равной 9000Гц. Запустить модель на цикл моделирования и выполнить п.3. Возможно ли восстановление передаваемых сообщений в этом случае? Объяснить причину наблюдаемых явлений.

ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ

5. Изучить материал лабораторной работы по методическим указаниям и рекомендованной литературе.

6. В черновой тетради подготовки к лабораторным работам привести:

- схему исследуемой модели;

- расчет максимальной частоты дискретизации для каждого из передаваемых сообщений;

- спектры мощности сигналов выделяемой на резисторе в 1 Ом и описывающих передаваемые сообщения, если их амплитуда равна 2В;

- обоснование минимальной частоты тактовых генераторов при которой обеспечивается восстановление всех передаваемых сообщений;

4. Ответить на вопросы контрольного задания.

СОДЕРЖАНИЕ ОТЧЕТА.

1. Наименование работы, ее цель и задачи.

2. Структурная схема модели, ее параметры, параметры системного времени.

3. Эскизы графиков сигналов, их спектров с указанием полученных оценок параметров, а так же выводы в соответствии с пунктами 1…7 «Хода выполнения работы».

4.Выводы по работе в целом.

ЛИТЕРАТУРА.

1. Кловский Д.Д. Теория передачи сигналов. Стр. 319…321.

2. Зюко А.Г. и др. Теория передачи сигналов. Стр.64…70, 265…268.

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Каким обязательным требованиям должны удовлетворять параметры канальных модулей в системе с временным разделением?

2. Одинаковы ли условия работы различных каналов системы? Ответ обосновать, сравнивая работу соседних каналов.

3. Как влияет увеличение числа одновременно работающих каналов на работу линейного оборудования? Ответ обосновать, принимая во внимание, что в составе линейного оборудования могут быть усилители, преобразователи и другие активные устройства.

4. Оценить ширину полосы частот требуемую для передачи тех же сообщений, что и в данной работе, но с использованием частотного разделения. Какой вариант трехканальной системы потребует большей полосы и почему?

ЛАБОРАТОРНАЯ РАБОТА №4

ПЕРЕНОС СПЕКТРОВ СИГНАЛОВ В СУПЕРГЕТЕРОДИННОМ РАДИОПРИЕМНИКЕ.

Цель работы: Изучить реализацию принципа переноса спектров в супергетеродинном радиоприемнике.

Задачи работы :

1. Изучить функции основных узлов супергетеродинного радиоприемника как системы с частотным разделением каналов.

2. Изучить реализацию функций частотной селекции по соседнему и зеркальному каналам в супергетеродинном радиоприемнике на основе

3. принципа переноса спектра сигнала.

ВВЕДЕНИЕ.

Технология супергетеродинного радиоприема находит широкое применение в системах радиосвязи, в частности, спутниковой, УКВ телефонии, КВ магистральной cвязи и т.д. . Упрощенная структурная схема супергетеродинного радиоприемника приведена на рис.1.

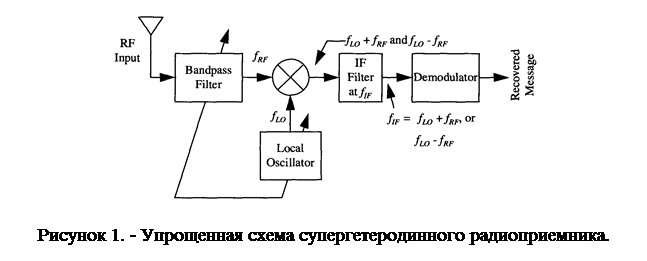Входной сигнал приемника (RF Input) поступает на входной полосовой фильтр (Bandpass Filter) , где выделяется диапазон принимаемых частот и подавляются сигналы зеркального канала. С выхода этого фильтра сигналы выделенной полосы частот поступают на смеситель, куда поступает так же гармонический сигнал местного генератора (Local Oscillator). Здесь осуществляется смещение спектров принимаемых сигналов, формирование полос суммарной и разностной частот. Фильтр промежуточной частоты (IF Filter) выделяет спектр принимаемого сигнала из состава одной из полос

(в данной работе - разностной) и передает на вход демодулятора (Demodulator), где и восстанавливается передаваемое сообщение (Recovery Message).

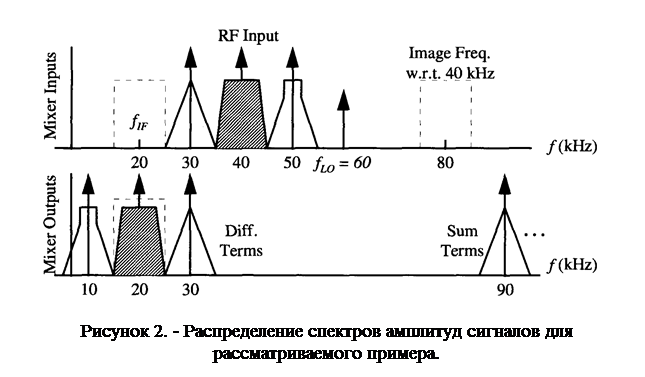
Для примера в данной лабораторной работе рассматривается выделение сообщений из суммы амплитудно-модулированных сигналов с несущими частотами () 30, 40 и 50кГц (См. рис. 2).

Промежуточная частота выбрана равной 20кГц. Аналоговое сообщение занимает полосу частот менее 5кГц. Полосовой фильтр на входе приемника предназначен для подавления нежелательных шумов и сигналов в зеркальной полосе частот, отстоящей от частоты приема на 2,обеспечивая тем самым селекцию по зеркальному каналу. Селекция по соседнему каналу обеспечивается полосовым фильтром промежуточной частоты (IF Filter), который имеет фиксированную настройку. Выбор частоты принимаемого сигнала осуществляется синхронной перестройкой частоты местного генератора гармонического колебания (Local Oscillator) - гетеродина и настройки полосового фильтра на входе приемника.

Предположим, нам необходимо принять сигнал с частотой несущего колебания 40кГц. Гетеродин должен быть настроен на частоту 20+40=60кГц, середине зеркального канала будет соответствовать 2(20)+40=80кГц. Спектр принимаемого сигнала окажется в пределах полосы пропускания фильтра промежуточной частоты.

Спектры сигналов с несущими частотами 30 и 50кГц будут перенесены в области 10 и 30кГц, т.е. за пределы полосы пропускания фильтра и будут им подавлены. Фильтром будет выделен спектр только одного передатчика - с частотой несущего колебания 40кГц. Демодуляция выходного сигнала фильтра позволяет получить передаваемое сообщение.

Данная работа направлена на изучение процессов преобразования спектров сигналов в супергетеродинном приемнике средствами пакета System View.

ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ.

Объектом исследования в данной работе является модель супергетеродинного приемника (См. рис. 3). Передаваемые сообщения в модели представлены гармоническими колебаниями, частоты которых изменяются по линейному закону.

В состав модели системы входят модули передатчиков, представленных на левой части рисунка и приемника – на правой части. Среда распространения – эфир представлена сумматором сигналов. Задачи данной работы реализуются путем анализа сигналов в различных точках модели, их сопоставления и оценки как во временной, так и в частотной областях. При проведении исследований предусматривается изменение параметров настройки некоторых модулей модели, а так же дополнение модели модулем входного фильтра.

ХОД ВЫПОЛНЕНИЯ РАБОТЫ.

1.

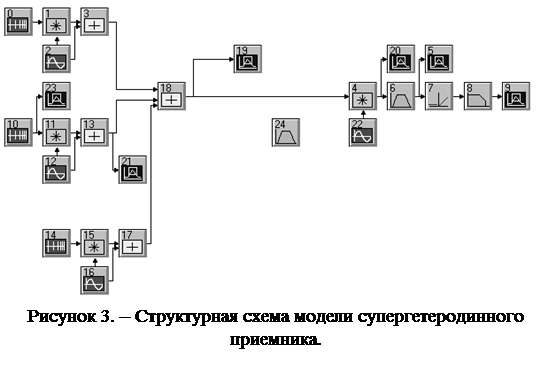Загрузить исполняющий файл Com_amr1.svu. Зарисовать структуру модели, записать параметры ее модулей, параметры системного времени.

2. Запустить модель на цикл моделирования. Получить графики исходных сообщений (Sink23) и оценить параметры сигналов, которые их представляют (Sink 21).

3. Получить график сигнала на входе приемника (Sink19) и его спектр. Анализируя картину спектра, определить области частот занимаемые сигналами каждого из передатчиков. Оценить ширину спектра каждого передаваемого сигнала на уровне –10дБ относительно максимального уровня боковых полос для каждого из сигналов.

4. Получить график сигнала на выходе смесителя (Sink20). Оценить степень смещения спектров сигналов относительно входных, сопоставить картину спектров сигналов на входе приемника и на выходе смесителя.

5. Получить график сигнала на выходе фильтра промежуточной частоты (Sink5). Сопоставить картину спектров сигналов на входе фильтра и на его выходе. Повысить порядок фильтра с 5-го до 9-го и, повторно запустив модель на цикл моделирования сопоставить вновь полученные спектры между собой. Сравнить оба варианта реализации фильтра по способности подавлять сигналы передатчиков соседних каналов.

6. Получить график принятого сообщения на выходе приемника (Sink 9) и сравнить его с передаваемым (Sink21).Сделать выводы относительно возможности приема передаваемого сообщения.

7. Перестроить гетеродин приемника сначала на частоту 50кгц , а затем на частоту 70кГц (Модуль22).Выполнить п.6 Хода выполнения работы, учитывая при этом, что источниками сообщений будут модули 0 и 14, соответственно.

8. Перестроить генератор несущего колебания третьего передатчика на частоту 80кгц (Модуль16), а гетеродин приемника на 60кГц. Выполнить п.6 Хода выполнения работы и объяснить причину наблюдаемых явлений.

9. Установить полосовой фильтр на входе приемника (Модуль 24) , включив его между модулями 8 и 4. Выполнить п.6 Хода выполнения работы и объяснить причину наблюдаемых изменений в спектрах и сигналах.

СОДЕРЖАНИЕ ОТЧЕТА.

1. Наименование работы, ее цель и задачи.

2. Структурные схемы модели, ее параметры, параметры системного времени.

3. Эскизы графиков сигналов, их спектров с указанием полученных оценок параметров, а так же выводы в соответствии с пунктами 1…9 «Хода выполнения работы».

ЛИТЕРАТУРА.

1. Кловский Д.Д. Теория передачи сигналов. Стр.92…96.

2. Гоноровский И.С. Радиотехнические цепи и сигналы. Стр. 88…97.

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Как изменится работа приемно-передающей системы , если сигнал гетеродина будет отличен от гармонического?

2. Проанализируйте возможность реализации супергетеродинного радиоприемника с переносом спектра вверх, т.е. когда =+. Какие преимущества и недостатки имеет этот вариант реализации приемника?

3. Как должны соотносится между собой ,,, что бы частота зеркального канала стала отрицательной?

4. В каких случаях можно использовать фильтр низких частот в качестве входного фильтра приемника?

5. Допустим, что шум эфира имеет неограниченный по частоте равномерный спектр амплитуд. Как влияет использование входного фильтра на соотношение сигнал-шум на выходе приемника в этом случае? Дать качественную и количественную оценку влияния.

ЛАБОРАТОРНАЯ РАБОТА №5

ПЕРИОДОГРАММНЫЕ ОЦЕНКИ СИГНАЛОВ.

Цель работы: Изучить периодограммные методы оценки структуры и параметров сигналов.

Задачи работы:

1. Изучить методы спектральных оценок случайных процессов и их применение для получения периодограмм (Быстрое преобразование Фурье, получение спектров мощности, усреднение спектров);

2. Получить опыт спектральной оценки структуры и параметров сигналов содержащих случайную и регулярную компоненты на основе периодограммного анализа.

ВВЕДЕНИЕ.

Периодограммные методы оценки спектров сигналов, содержащих случайные и регулярные компоненты, широко используются на практике, как при анализе сигналов, так и при синтезе структуры средств связи и алгоритмов обработки информации. Являясь теми методами, которые связывают теорию электросвязи с практикой радиоизмерений и обработки сигналов, он позволяет наиболее просто оценить структуру и параметры регулярных компонент в составе сложного сигнала с требуемой достоверностью и получить экспериментальный материал, необходимый для проверки адекватности теоретических моделей. Периодограммные методы оценки получили широкое распространение, как в технике радиоизмерений, так и при реализации структуры и алгоритмов работы систем связи. Широкому внедрению этих методов в практику способствовало бурное развитие микропроцессорной техники и ПЭВМ. Структура метода периодограмм включает следующие элементы:

- Получение (нарезки) сегментов реализации исследуемого сигнала (случайного процесса) из достаточно протяженной (длинной) исходной реализации. Эти сегменты могут быть частично перекрывающимися по краям;

- Применение, при необходимости, к каждому сегменту временного окна;

- Получение спектра амплитуд каждого сегмента реализации. Для этих целей, как правило, используется алгоритм быстрого преобразования Фурье. Заметим, что получаемые спектры амплитуд являются случайными процессами относительно частоты;

- Получение спектров мощности для каждого сегмента реализации;

- Усреднение спектров мощности по всему множеству спектров.

Сформированный таким образом усредненный спектр характеризуется следующими особенностями:

- Будучи спектром, полученным на гармоническом базисе, он дает представление о структуре и распределении энергии гармонических компонент в составе сигнала;

- Отношение энергии регулярных и случайных компонент в таком спектре выше, чем в любом из спектров мощности для каждого обрабатываемого сегмента;

- Степень размытости, а, следовательно, и степень неопределенности оценки уровня спектральных компонент, определяющая достоверность получаемых оценок уровня при всех прочих равных условиях, зависит от количества усредняемых спектров;

- Чем больше спектров усредняется, тем меньше размытость, тем выше достоверность оценки уровня;

- При заданной протяженности исходной (длинной) реализации повышение достоверности оценки уровня за счет увеличения количества усредняемых спектров ограничено снижением разрешения по частоте. Таким образом, повышение достоверности оценки уровня окупается снижением достоверности оценки частоты. Одновременное повышение достоверности по обоим показателям невозможно без увеличения протяженности исходной реализации процесса.

ПОСТАНОВКА ЗАДАЧИ ИССЛЕДОВАНИЯ.

Исследование осуществляется на основе простой модели (См. рис.1), включающей модули формирования многокомпонентного сигнала, содержащего Гауссов белый шум, гармонические и импульсные компоненты и модули для получения периодограмм (модули получения спектра амплитуд, спектра мощности, статистической обработки). Эффект усреднения достигается за счет многократного повторения одного и того же алгоритма вычислений, осуществляемых моделью для каждой новой реализации процесса, рассматриваемой как очередной сегмент, и суммирования взвешенных спектров мощностей реализаций. Количество повторений задается на панели настроек системного времени пакета System View (параметр Nr. of Loop). Исследование заключается в получении спектральных оценок сигналов различной структуры при использовании усреднения спектров мощности и без такового. Сопоставление получаемых спектров и их параметров позволяет сделать выводы об эффективности метода и его особенностях.

ХОД РАБОТЫ.

1. Загрузить исполняющий файл dsp_aper.svu. Зарисовать структуру модели, записать параметры ее модулей, параметры системного времени. Дополнить модель модулем анализа, который подсоединить к выходу сумматора.

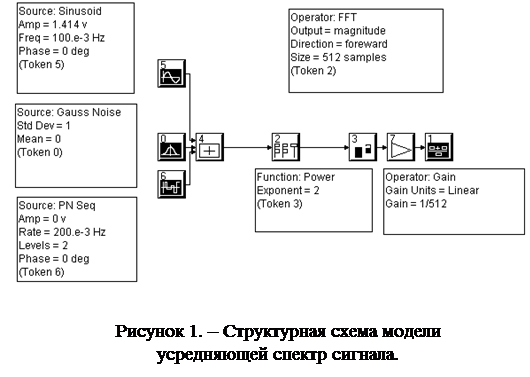2. Запустить модель на цикл моделирования. Получить график процесса усреднения спектра сигнала (Sink 1). Выделить участок, соответствующий окончательным результатам усреднения.

3. Выбирая область участка визуализации по оси абсцисс и переходя к логарифмическому масштабу по оси ординат выделить интересующий Вас участок графика (0…255), который и будет представлять усредненный спектр. Перейти к логарифмическому масштабу по оси ординат. Определить масштабный коэффициент по оси абсцисс, ориентируясь на известную частоту гармонической компоненты и отсчет по вышеуказанной оси графика, соответствующий пику спектра.

4. Оценить ширину зоны размытости (неопределенности) уровня спектральной плотности мощности у основания главного лепестка спектра. Оценить ширину главного лепестка спектра, сравнить со спектром реализации (Sink 8). Сделать выводы относительно разрешающей способности для каждого случая.

5. Установить амплитуду гармонической компоненты равной 0 и импульсной компоненты равной 2В (модули 5 и 6). Запустить модель на цикл моделирования. Получить график процесса усреднения спектра сигнала (Sink 1). Выделить участок, соответствующий окончательным результатам усреднения. Выполнить п.4 “Хода выполнения работы”.

6. Получить неусредненный спектр мощности (Sink 8), и сравнить его со спектром, полученным в п.5. Сделать выводы относительно эффективности метода периодограмм.

СОДЕРЖАНИЕ ОТЧЕТА.

1. Наименование работы, ее цель и задачи.

2. Структурная схема модели, ее параметры, параметры системного времени.

3. Эскизы графиков сигналов, их спектров с указанием полученных оценок параметров, а так же выводы в соответствии с пунктами 1…6 «Хода выполнения работы».

ЛИТЕРАТУРА.

1. Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения. Стр. 191…206.

2. Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем связи. Стр. 88…90.

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Проанализируйте на качественном уровне, какие имеются возможности для повышения разрешения по частоте за счет перекрытия сегментов реализации? Каковы ограничения этого метода и чем они обусловлены?

2. Как влияет использование взвешивающих окон на разрешение по частоте? Как повлияет совместное использование взвешивающего окна и перекрытия сегментов реализаций?

3. Что является принципиальным ограничением повышения достоверности оценки сигналов по уровню и частоте для периодограммного метода?

4. Постройте график спектра мощности трехкомпонентного сигнала, содержащего:

- синусоиду с частотой 0,1Гц и амплитудой 1,414 В,

- Гауссов белый шум с нулевым средним значением и СКО равным 1В,

- последовательность знакопеременных прямоугольных импульсов с частотой следования 0,2Гц и амплитудой 2В при скважности равной 1.

ЛАБОРАТОРНАЯ РАБОТА №6.

УЗКОПОЛОСНЫЕ СИГНАЛЫ И ИХ СВОЙСТВА.

Цель работы: Изучить узкополосные сигналы, их свойства, получение и применение в системах связи.

Задачи работы:

1. Изучить получение узкополосных сигналов методами модуляции и полосовой фильтрации.

2. Изучить свойства узкополосных сигналов, получаемых различными методами.

3. Исследовать особенности узкополосных сигналов, используемые в системах связи.

ВВЕДЕНИЕ.

В большинстве современных систем связи в качестве сигналов, передаваемых в среду распространения, используются узкополосные сигналы. Этому способствуют несколько причин. Среди них важнейшими являются:

- меньшая подверженность линейным искажениям,

- относительная простота реализации технических средств передачи и приема узкополосных сигналов,

- относительная простота алгоритмов обработки узкополосных сигналов.

Для узкополосного сигнала выполняется соотношение

,

где, - центральная частота спектра сигнала,

-ширина спектра сигнала.

Такой сигнал может быть получен одним из двух способов:

-Узкополосной модуляцией гармонического несущего колебания. Для этого необходимо, что бы выполнялось условие

,

где, - максимальная частота в спектре модулирующего сигнала,

- частота несущего колебания;

-Узкополосной полосовой фильтрации широкополосного сигнала, например, шумового. Для этого необходимо выполнение условия

,

где, - полоса пропускания полосового фильтра,

-центральная частота полосы пропускания фильтра.

Характерным для узкополосного сигнала является высокая степень коррелированности соседних периодов колебания. При сужении полосы происходит гармонизация колебания, то есть заполнение колебания близко по форме к косинусоиде, соседние максимумы имеют близкое значение. Если построить кривую, проходящую через вершины косинусоид, то окажется, что построенная таким образом огибающая изменяется много медленнее, чем заполнение.

Для таких сигналов используется представление в виде

,

где, - огибающая (меняющаяся амплитуда),

- мгновенная фаза колебания.

Спектр узкополосного сигнала, полученного путем модуляции гармонического переносчика для простейших видов модуляции симметричен относительно несущей частоты. Для восстановления информации, содержащейся в таком сигнале, достаточно половины его спектра. Узкополосные сигналы, полученные путем фильтрации широкополосных, как правило , этому требованию не удовлетворяют.

Узкополосные сигналы при распространении в некоторой среде претерпевают меньшие линейные искажения, чем широкополосные, что связано с тем, что среда распространения, в пределах узкого диапазона частот, занимаемого сигналом, имеет примерно одинаковые свойства по отношению ко всем его частотным компонентам.

Современные технологии, применяемые при создании средств связи, широко используют явления электрического и механического резонанса для реализации элементов частотной селекции сигналов (полосовых фильтров). Наиболее просты и дешевы - узкополосные фильтры, а широкое использование таких фильтров в аппаратуре связи предопределяет (наряду с другими факторами) выбор проектировщиков в пользу узкополосных сигналов,

ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ.

Объектом исследования в данной работе являются узкополосные сигналы, формируемые и обрабатываемые в одной из двух простых моделей систем (см. рис.1).

Первая модель воспроизводит процесс формирования узкополосного сигнала методом полосовой фильтрации из широкополосного Гауссова белого шума. Изменение полосы фильтрации позволяет наблюдать изменение свойств профильтрованного сигнала в частотной и временной областях.

Вторая модель представляет процесс формирования узкополосного сигнала с помощью модуляции и его распространения в среде с частотно-зависимыми свойствами. На основании сравнения результатов прохождения сигналов, несущих одно и то же сообщение через одну и ту же среду можно сделать вывод, что преобразование исходного широкополосного сигнала в узкополосный дает определенный выигрыш в смысле сохранения передаваемой информации.

Задачи данной работы реализуются путем анализа сигналов в различных точках моделей, их сопоставления и оценки как во временной, так и в частотной областях.

ХОД ВЫПОЛНЕНИЯ РАБОТЫ.

1. Загрузить исполняющий файл модели 1 rr_noise.svu. Зарисовать структуру модели, записать параметры ее модулей, параметры системного времени. Запустить модель на цикл моделирования. Получить графики сигналов на выходах фильтров, их спектры и корреляционные функции.

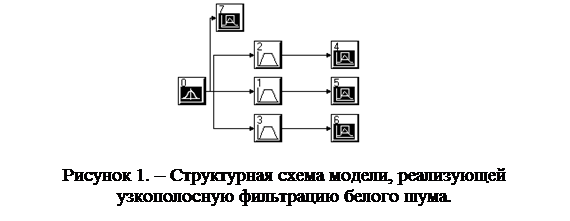2. Оценить ширину спектров на уровне -60dB. Сделать выводы относительно изменения формы сигнала при изменении полосы фильтрации.

3. Оценить среднюю скорость нарастания огибающей сигнала на выходе каждого фильтра, используя выражение

,

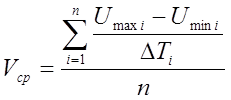где, и - уровни смежных максимумов квазигармонического заполнения (несущего колебания) сигнала,

- временной интервал между смежными max и min сигнала,

- номер измерения ()

4. Сопоставить результаты оценок по пп.2,3 и сделать выводы о взаимосвязи полосы сигнала и скорости изменения его огибающей.

5. Загрузить исполняющий файл модели 2 - fpulse2.svu. Зарисовать структуру модели, записать параметры ее модулей, параметры системного времени.

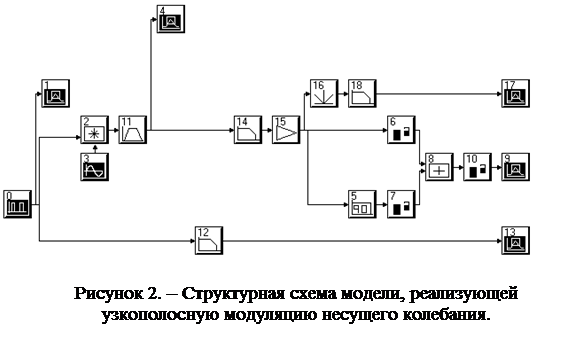6. Запустить модель на цикл моделирования и получить графики сигналов, воспроизводящих исходное (передаваемое) и полученное сообщения. Сделать выводы об искажении узкополосного и широкополосного сигналов, несущих одну и ту же информацию прохождении через одну и ту же среду распространения.

7. Дать оценку качеству восстановления исходного сигнала детектором огибающей и средствами обработки аналитического сигнала.

СОДЕРЖАНИЕ ОТЧЕТА.

1. Наименование работы, ее цель и задачи.

2. Структурная схема моделей, их параметры, параметры системного времени.

3. Эскизы графиков сигналов, их спектров с указанием полученных оценок параметров.

4. Выводы в соответствии с пунктами 1…7 «Хода выполнения работы».

ЛИТЕРАТУРА.

1. Зюко А.Г. и др. Теория передачи сигналов. Стр.45…54.

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Почему представление сигнала в виде

считается неоднозначным и как эта неоднозначность устраняется при представлении этого сигнала как аналитического?

2. Почему применение аппарата аналитического сигнала к классу узкополосных сигналов наиболее эффективно?

3. Какие параметры комплексной огибающей несут информацию о сообщении при: -1- амплитудной модуляции, -2- при угловой модуляции?

4. Какие изменения претерпевает корреляционная функция сигнала по мере сужения его полосы?

ЛАБОРАТОРНАЯ РАБОТА №7.

ПРОХОЖДЕНИЕ ДЕТЕРМИНИРОВАННЫХ И СЛУЧАЙНЫХ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЗВЕНЬЯ КАНАЛОВ СВЯЗИ.

Цель работы: Изучить преобразование детерминированных и случайных сигналов при прохождении их через линейные звенья каналов связи.

Задачи работы:

1. Исследовать характеристики и свойства линейных звеньев при обработке ими регулярных сигналов.

2. Исследовать характеристики линейных звеньев при обработке ими случайных сигналов.

ВВЕДЕНИЕ.

Линейные свойства каналов связи часто представляют моделями в виде фильтров. Кроме того, фильтры как элементы средств связи являются важными и распространенными компонентами современной аппаратуры. Знание основных разновидностей фильтров, процессов преобразования сигналов фильтрами (т.е. процессов фильтрации) и характеристик фильтров совершенно необходимо для анализа и синтеза систем связи.

Основными характеристиками фильтра являются амплитудно-частотная (АЧХ)

и фазочастотная (ФЧХ)

где, -

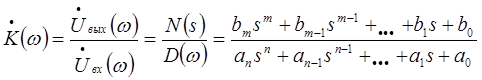комплексный коэффициент передачи фильтра, - комплексная частота, - порядок фильтра ().

В зависимости от вида амплитудно-частотной характеристика фильтры подразделяются на:

-фильтры нижних частот - ФНЧ - (пропускают сигналы с частотой ниже частоты среза ),

-фильтры верхних частот - ФВЧ - (пропускают сигналы с частотой выше частоты среза ),

-полосовые фильтры - ПФ - (пропускают сигналы в полосе частот ),

-заграждающие фильтры - ЗФ - (пропускают сигналы за пределами полосы заграждения ).

Свойства фильтра в значительной степени определяются полюсами комплексного коэффициента передачи, в связи с этим корни полинома знаменателя играют решающую роль в описании фильтра. В зависимости от вида аппроксимирующего полинома знаменателя выделяют следующие разновидности фильтра:

-Баттерворта,

-Бесселя,

-Чебышева и др.

Структура фильтров может быть одной и той же, однако, различия в коэффициентах полиномов числителя и знаменателя, а следовательно и корнях полиномов существенно влияют на свойства фильтров.

Среди простых линейных звеньев, которые могут быть представлены через общее описание фильтра, выделены наиболее часто встречающиеся. Это -

1. Пропорциональное звено (ФНЧ, у которого для всех а для всех )

2. Интегратор (ФНЧ, у которого для всех а для всех )

3. Дифференциатор (ФВЧ, у которого для всех а для всех )

4. Инерционное звено (ФНЧ, у которого для всех а для всех , кроме )

5. Колебательное звено (ПФ, у которого для всех а для всех , кроме ).

Данная работа направлена на изучение свойств фильтров как моделей звеньев систем связи средствами пакета SystemView.

ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ

Объектом исследования в данной работе являются ФНЧ, ФВЧ и ПФ, находящиеся под воздействием гармонических, импульсных и случайных сигналов.

Проходящие через фильтр гармонические компоненты входного сигнала претерпевают в фильтре ослабление (усиление) и задержку во времени, в результате чего спектр сигнала на выходе фильтра может существенно отличаться от формы входного сигнала

Эти изменения могут приводить как к положительным результатам в работе реальных систем связи (подавление нежелательных компонент, очистка сигнала то помех), так и отрицательным (линейные искажения). Выбирая нужную разновидность фильтра и его параметры (порядок фильтра, частоты среза) можно достигнуть желаемых свойств и тем обеспечить необходимое качество фильтрации.

Схема модели для исследования фильтра элементарно проста. Это последовательное соединение модулей генератора входных сигналов (- функция, меандр, синусоида, Гауссов белый шум), собственно фильтра и регистратора выходных сигналов (анализирующее окно пакета SystemView).

Задачи данной работы реализуются путем анализа входных и выходных сигналов фильтра во временных и частотных областях для вышеуказанных разновидностей и структур фильтров при стандартных сигналах подаваемых на вход.

ХОД ВЫПОЛНЕНИЯ РАБОТЫ.

1.

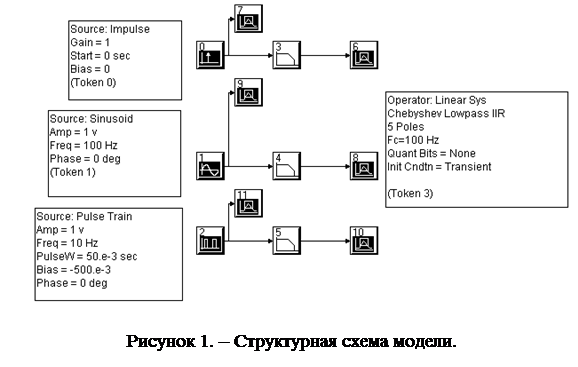Загрузить исполняющий файл dsp_fil1.svu (Рис.1). На экране ПЭВМ появится структура трех моделей для исследования прохождения стандартных сигналов, а именно, - функции, синусоиды и меандра, через фильтр.

Используя средства редактирования моделей, ввести еще одну четвертую модель - для исследования прохождения Гауссова белого шума через такой же фильтр (среднеквадратическое значение шума принять равным 1).

2. Зарисовать структуру моделей, записать параметры модулей, параметры системного времени. Запустить модели на цикл моделирования. Получить графики сигналов на выходах фильтров.

3. Исследовать прохождение стандартных сигналов через ФНЧ, а именно:

4. Используя импульсную переходную функцию, получить АЧХ и ФЧХ фильтра и по ним частоту среза. Рассмотреть случаи фильтров Баттерворта, Бесселя и Чебышева. Дать качественное сравнительное описание особенностей АЧХ и ФЧХ рассматриваемых разновидностей фильтров.

5. Оценить временную задержку, вносимую фильтрами. Исследовать зависимость этой задержки от порядка фильтра и построить график зависимости.

6. Исследовать особенности прохождения гармонического сигнала через фильтр. Качественно описать вносимые фильтром искажения.

7. Исследовать особенности прохождения через фильтр сигнала типа меандр. Качественно описать и объяснить вносимые фильтром искажения. Рассмотреть случаи фильтров Баттерворта, Бесселя и Чебышева. Неравномерность в полосе прозрачности принять равной 0,5 дБ. Проанализировать связь между нелинейностью фазовой характеристики, крутизной амплитудной и вносимыми фильтром искажениями. Рассмотреть случаи изменения порядка фильтра.

8. Исследовать особенности прохождения Гауссова белого шума через ФНЧ. Сравнить автокорреляционную функцию выходного сигнала с автокорреляционной функцией Гауссова белого шума. Исследовать зависимость главного лепестка автокорреляционной функции от частоты среза фильтра, построить график этой зависимости.

9. Выполнить исследования согласно пп.3.1, 3.2, 3.3 и 3.5 применительно к ПФ. Частоты среза ПФ принять 80 Гц и 120 Гц.

10. Выполнить исследования согласно пп.3.1, 3.2, 3.3 и 3.5 применительно к ФВЧ. Частоту среза фильтра принять равной 100 Гц.

11. Исследовать прохождения стандартных сигналов через интегратор, дифференциатор, пропорциональное, инерционное и колебательные звенья. Дать качественное описание выходным сигналам для каждого стандартного входного сигнала. Во всех необходимых случаях принимать единичные значения коэффициентов и нулевые начальные условия. В качестве колебательного звена использовать ПФ первого порядка с частотами среза 80 и 120 Гц.

СОДЕРЖАНИЕ ОТЧЕТА.

1. Наименование работы, ее цель и задачи.

2. Структурная схема моделей, их параметры, параметры системного времени.

3. Эскизы графиков сигналов, их спектров, автокорреляционные функции, АЧХ и ФЧХ, построенные зависимости, необходимые комментарии в соответствии с пп.1-11.

4. Выводы в соответствии с пунктами 1-11 «Хода выполнения работы».

ЛИТЕРАТУРА.

1. Фельдбаум А.А. и др. Теоретические основы связи и управления. Стр. 166-197.

2. Мошиц Г., Хорн П., Проектирование активных фильтров. Стр. 13-26.

ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ.

1. В конспекте лекций привести формулы для комплексного коэффициента передачи ФНЧ, ФВЧ, ПФ второго порядка, а так же для интегратора, дифференциатора, пропорционального, инерционного колебательного звеньев в случае, когда кроме .

2. Для вышеперечисленных звеньев в конспекте привести качественные графики зависимостей АЧХ и ФЧХ.

ЛАБОРАТОРНАЯ РАБОТА №8

ИССЛЕДОВАНИЕ УГЛОВОЙ МОДУЛЯЦИИ ГАРМОНИЧЕСКОГО НЕСУЩЕГО КОЛЕБАНИЯ

Цель работы: Изучить преобразование сигналов при угловой модуляции - демодуляции.

Задачи работы:

1. Изучить основы получения частотно-модулированных сигналов и восстановления исходных сообщений из них.

2. Изучить основы получения и детектирования фазомодулированных сигналов.

3. Дать сравнительную оценку методам угловой модуляции.

ВВЕДЕНИЕ.

Общепринятым представлением модулированного сигнала в технике связи является

,

где - амплитуда, а - полная фаза колебания,

- начальная фаза и частота.

Если , а изменяется во времени по закону передаваемого сообщения , то имеет место угловая модуляция несущего колебания. Различают два вида угловой модуляции - частотную (ЧМ) и фазовую (ФМ). Связь этих двух видов модуляции определяется соотношениями

или ,

из которых следует, что изменения частоты и фазы взаимно определяют друг друга.

При ЧМ мгновенное значение частоты

связано с модулирующим сигналом (сообщением) линейной связью ( - значение при ).

Полная фаза ЧМ сигнала будет равна

.

С учетом этого выражение для ЧМ сигнала имеет вид

При ФМ мгновенное значение фазы

связано с модулирующим сигналом (сообщением) линейной связью. Тогда для ФМ сигнала имеем

При модуляции однотоновым сигналом с частотой

по характеру модулированного колебания нельзя заключить с какой модуляцией мы имеем дело: ЧМ или ФМ. В то же время различие между ЧМ и ФМ проявляется при изменении частоты модуляции или при одновременной модуляции полосой частот.

При ЧМ величина девиации частоты , т.е. максимальное отклонение относительно , зависящая только от амплитуды модулирующего сигнала, остается постоянной при изменении частоты модуляции .

При ФМ девиация частоты изменяется прямо пропорционально частоте модуляции .

Если модуляция осуществляется не одним гармоническим, а сложным сигналом, то структура модулированного колебания будет различной для ЧМ и ФМ.

При ЧМ обычно применяется прямое воздействие на частоту колебаний задающего генератора передатчика. В случае ФМ задающий генератор вырабатывает стабильную частоту, а фаза колебаний модулируется в одном из последующих каскадов передатчика (например, в предварительном усилителе).

В современной технике ЧМ широко используется в средствах низовой мобильной связи, а некоторые разновидности ФМ, например, фазоразностная, получили распространение в системах цифровой связи.

ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ.

Объектом исследования в данной работе является простейшая истема, содержащая частотный (фазовый) модулятор и демодулятор (см. рис.1). В качестве демодулятора используется квадратурный детектор, применяемый при узкополосной ЧМ и ФМ.

Задачи данной работы реализуются путем анализа модулированных сигналов и получаемых сообщений для задаваемого набора сообщений, подлежащих передаче. При этом оцениваются параметры спектров модулированных сигналов и получаемых сообщений, нелинейные искажения принятых сигналов, осуществляется сравнительная оценка вышеуказанных сигналов и спектров при ЧМ и ФМ.

ХОД ВЫПОЛНЕНИЯ РАБОТЫ

1. Загрузить исполняющий файл сом_quad.svu. Дополнить модель регистратором передаваемого сообщения. Зарисовать структуру модели, записать параметры модулей, параметры системного времени. Запустить модель на цикл моделирования. Получить графики регистрируемых сигналов, спектры передаваемого модулированного и принятого сигналов.

2. Оценить коэффициент нелинейных искажений для принятого сигнала

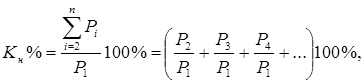
где - мощность -ой гармоники сигнала.

3. Построить зависимости коэффициента нелинейных искажений от:

- величины сигнала сообщения (рекомендуемый диапазон от 0.5 до 5В),

- частоты несущего колебания (рекомендуемый диапазон - Гц).

Для уменьшения влияния явления утечки на оценку слабых компонент высших гармоник использовать временное окно Ханнинга. Дать анализ изменениям спектра модулированного сигнала, его структуры и уровня частотных компонент при изменении величины передаваемого сигнала.

4. Заменить источник гармонического передаваемого сигнала на источник сигнала с изменяющейся частотой (Freq.Sweap) с параметрами: Amp=1B, Start.Frq=5Hz, Stop.Frq=15 Hz, Period=0.64 s, Phase=0 deg.

Запустить модель и сопоставить передаваемое и принятое сообщения. Объяснить искажения принятого сигнала и предложить меры по уменьшению искажений. Реализовать предложения на модели и оценить их эффективность.

5. Заменить частотный модулятор на фазовый и выполнить п.п. 2, 3, 4.

6. По результатам исследования ЧМ и ФМ сигналов, их спектров и получаемых при этом сообщений дать сравнительную характеристику особенностям рассмотренных видов модуляции.

СОДЕРЖАНИЕ ОТЧЕТА.

1. Наименование работы, ее цель и задачи.

2. Структурные схемы моделей, их параметры, параметры системного времени.

3. Эскизы графиков сигналов, их спектров, построенные зависимости, необходимые комментарии в соответствии с п.п. 1-6.

4. Выводы в соответствии с пунктами 1-6 «Хода выполнения работы».

ЛИТЕРАТУРА.

1. Фельдбаум А.А. и др. Теоретические основы связи и управления. Стр. 85-97.

ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ.

1. Выполнить на качественном уровне сравнение спектра АМ колебания со спектрами ФМ и ЧМ сигналов для случая, когда передается сообщение вида

.

Проанализировать возможность управления полосой, занимаемой модулированными сигналами в линии связи для каждого вида модуляции.

ЛАБОРАТОРНАЯ РАБОТА №9

ИССЛЕДОВАНИЕ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ БЕЗЫНЕРЦИОННЫМИ НЕЛИНЕЙНЫМИ ЗВЕНЬЯМИ

Цель работы: Изучить преобразовательные свойства безынерционных нелинейных звеньев.

Задачи работы:

1. Исследовать преобразования регулярных сигналов безынерционными нелинейными звеньями.

2. Исследовать прохождения стационарных случайных процессов через безынерционные нелинейные звенья.

ВВЕДЕНИЕ.

Нелинейные элементы, используемые в технике связи и имеющие гладкие статические характеристики описываются обычно степенным рядом

Так как интерес представляет, как правило, изменение сигнала - постоянная составляющая из рассмотрения исключается. Для уменьшения громоздкости вычислений, во внимание принимаются слагаемые со степенью, не выше второй. С учетом этого

В спектральной области входному сигналу соответствует сигнал на выходе нелинейного элемента

Классическим сигналом, прохождение через нелинейность которого, исследуется, является сигнал с ограниченным равномерным спектром

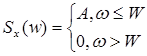
здесь

Спектр мощности квадратичной составляющей выходного сигнала имеет вид

,

где

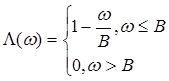
- константа, определяемая шириной спектра входного сигнала.

Результирующий спектр мощности выходного сигнала будет иметь вид

Классическими регулярными сигналами, прохождение через нелинейность которых исследуется, являются гармонический сигнал и сумма двух гармонических компонент с различными частотами.

.

Для гармонического входного сигнала на выходе нелинейного звена имеем

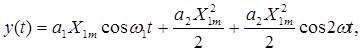
из чего видно, что выходной сигнал приобретает дополнительно постоянную составляющую и вторую гармонику. Если на входе нелинейного звена действует сигнал, содержащий две гармонические компоненты, то

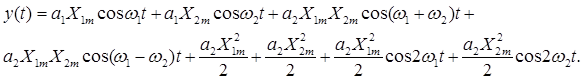
Из вышеприведенного соотношения следует, что наряду с дополнительной постоянной составляющей и компонентами удвоенной частоты выходной сигнал имеет компоненты с суммарной и разностной частотами, являющимися продуктами взаимодействия двух гармонических компонент входного сигнала на нелинейности.

Такое взаимодействие в реальной системе связи может привести к негативным последствиям - появлению нежелательных компонент в спектре выходного сигнала, другим негативным следствием упомянутого взаимодействия сигналов может быть подавление слабого сигнала сильным. Рассмотренные выше эффекты в нелинейных звеньях используются также и с положительным результатом в умножителях частоты, смесителях и т.д.

Примером негладкой (существенной) нелинейности является нелинейность типа ограничение.

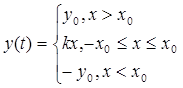
Звеном с такой характеристикой обычно моделируют усилители, ограничители сигналов и т.д.

ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ.

Объектом исследования в данной работе является простейшая структура (Рис.2), содержащая нелинейные элементы с рассмотренными выше характеристиками, источник входного сигнала и регистраторы. В качестве входного сигнала используются гармонические, - функция и Гауссов белый шум.

Задачи данной работы реализуются путем анализа в частотной области выходных сигналов нелинейностей для различных входных.

ХОД ВЫПОЛНЕНИЯ РАБОТЫ.

1. Загрузить исполняющий файл com_nlin.svu. Дополнить модель еще одним нелинейным модулем с характеристикой ограничение. Начальное значение уровня ограничения принять равным , уровень выходного сигнала

2. Построить графики спектров сигналов на входах и выходах нелинейностей для входного сигнала типа - функция, Гауссов белый шум , гармонический сигнал и двухкомпонентный сигнал . Объяснить картину спектра сигнала на выходе каждой нелинейности. Отметить характерные точки на графиках спектров (частоты, уровни).

3. Исследовать явление подавления слабого сигнала сильным сигналом , Построить график зависимости. Исследование провести для каждой нелинейности.

СОДЕРЖАНИЕ ОТЧЕТА.

1. Наименование работы, ее цель и задачи.

2. Структурная схема моделей, их параметры, параметры системного времени.

3. Эскизы графиков сигналов, их спектров, построенные зависимости и необходимые комментарии в соответствии с п.п. 1-3.

4. Выводы в соответствии с пунктами 1-3 «Хода выполнения работы».

ЛИТЕРАТУРА.

1. Зюко А.Г. и др. Теория передачи сигналов. Стр. 80-82.

2. Тихонов В.И. Статистическая радиотехника. Стр. 189-191.

ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ.

1. Построить график закона распределения выходного сигнала нелинейности типа ограничения с параметрами при подаче на его вход Гауссова белого шума с параметрами:

1.1.

1.2.

1.3.

ЛАБОРАТОРНАЯ РАБОТА №10

СИСТЕМЫ ФАЗОВОЙ АВТОПОДСТРОЙКИ ЧАСТОТЫ (ФАПЧ) В ТЕХНИКЕ СВЯЗИ

Цель работы: Изучить свойства и характеристики системы ФАПЧ.

Задачи работы:

1. Исследовать свойства и характеристики системы ФАПЧ при использовании ее в качестве частотного детектора.

2. Исследовать свойства и характеристики системы ФАПЧ при использовании ее в качестве управляемого генератора гармонических колебаний.

ВВЕДЕНИЕ.

Система ФАПЧ реализуются на основе элементарных звеньев соединенных в структуру с обратной связью. В состав ФАПЧ входит фазовый детектор (Ph.Det), формирующий фильтр (Loop Filter) и генератор гармонических колебаний, управляемый напряжением (VCO)- (см. рис.1). При использовании ФАПЧ в составе синтезатора частоты гетеродина, входным сигналом ФАПЧ является задающее гармоническое колебание X_V (t), выходным - сигнал местного генератора (VCO)-e₀ (t). Если ФАПЧ используется в качестве детектора ЧМ сигнала, входным сигналом является ЧМ сигнал X_V (t), выходным низкочастотный сигнал , представляющий восстанавливаемое сообщение.

Свойства и характеристики системы ФАПЧ определяются свойствами и характеристиками ее элементов, прежде всего фазовым детектором и формирующим фильтром. Существенное влияние на работу ФАПЧ оказывает передаточная характеристика фазового детектора, тип фильтра, его порядок, коэффициент передачи в петле обратной связи и др. Эти факторы влияют на условия захвата и удержание частоты, на нелинейные искажения при детектировании, на спектральный состав сигнала, генерируемого управляемым генератором.

ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ.

Объектом исследования в данной работе является простейшая система ФАПЧ, в которой в качестве управляемого генератора (VCO) используется частотный модулятор. Исходная схема модели (См. рис. 2) рассчитана на исследование ее как частотного детектора. Модель включает источник ЧМ сигнала (модули 2 и 3) и собственно модель ФАПЧ (модули 0,1,4,5). При проведении исследований модели источник сигнала и модель ФАПЧ модифицируются путем изменения параметров модулей, их замены и введение в состав структуры других модулей.

Задачи данной работы решаются путем анализа сигналов для различных точек модели ФАПЧ во временной и частотной областях, а также получение на этой основе оценок параметров самой ФАПЧ. При выполнении исследований, в частности, при оценке спектров, необходимо использовать нужные отрезки реализации сигналов, характерные для того или иного варианта использования ФАПЧ. Так при оценке нелинейных искажений, вносимых ФАПЧ при демодуляции, следует учитывать переходный режим ФАПЧ (соответственно, участок реализации, где этот режим наблюдается). При исследовании установившихся режимов, характерных для работы ФАПЧ в составе управляемого генератора, следует выбирать фрагменты реализации, где переходные процессы закончились.

ХОД ВЫПОЛНЕНИЯ РАБОТЫ

1. Загрузить исполняющий файл com_pll3.svu (Рис.2). Дополнить модель анализирующим модулем для регистрации модулирующего сигнала. Запустить модель на цикл моделирования и построить графики передаваемого и принятого сообщений и их спектры. (Для улучшения разрешения по частоте следует использовать временные окна и изменение масштаба по оси частот.) Определить время переходного процесса в системе ФАПЧ и коэффициент нелинейных искажений выходного сигнала частотного детектора. Во внимание принимать первые три гармоники модулирующего сигнала.

2. Исследовать влияние разновидностей (типа) используемого формирующего фильтра на время переходного процесса, заменяя фильтр Бесселя, на фильтр Баттерворта, затем – Чебышева (неравномерность частотной характеристики - 0,1дБ). Порядок и настройки фильтра сохранить те же.

Используя в качестве формирующего фильтр Чебышева, изменяя его порядок от 3 (исходное значение) до 8, построить зависимость времени переходного процесса и коэффициента нелинейных искажений от порядка фильтра.

3. Исследовать зависимость времени переходного процесса и коэффициента нелинейных искажений от изменения коэффициента усиления в петле обратной связи. Для этого целесообразно вернуться к исходному значению порядка фильтра (3) и, изменяя коэффициент усиления усилителя, (модуль 4) регистрировать время переходного процесса и спектр выходного сигнала. Последний дает возможность рассчитать коэффициент нелинейных искажений. Оценить максимальный коэффициент усиления, при котором еще обеспечивается устойчивая работа ЧМ детектора.

4. Заменить источник ЧМ сигнала источником гармонического колебания (амплитуда -1,414 В, частота – 1кГц). Дополнительно ввести анализирующий модуль для регистрации выходного - сигнала генератора управляемого напряжения. Получить оценки спектров сигналов задания и сигнала формируемого ФАПЧ как управляемого генератора. Сравнить спектры и оценить уровень нежелательных (паразитных) компонент в выходном сигнале ФАПЧ. Исследовать зависимость уровня второй гармоники в спектре выходного сигнала ФАПЧ от порядка формирующего фильтра Бесселя (порядок изменять от 3 до 8). Построить график этой зависимости.

5. Для исследования явления захвата и удержания задающего колебания следует дополнить исходную модель (файл com_pll3.svu) элементами, моделирующими перестройку частоты несущего колебания на входе ФАПЧ. Для этого между источником ЧМ сигнала (модуль 2) и входом ФАПЧ (модуль 3) следует поместить фрагмент схемы моделирующий перестройку частоты, изображенный на рис. 3.

Параметры дополнительно введенных модулей.

а) Параметры генератора ЛЧМ сигнала (Freq. Sweep):

Amp = 1B

Start.freq = 1.9КГц

Stop.freq = 2.15КГц

Period = 0.5с

б) Параметры полосового фильтра (Band Pass):

Тип – Баттерворт

Порядок – N=5

Частоты среза f_LO = 750Гц, f_HI = 1500 Гц.

Частоту генератора передаваемого сообщения следует увеличить до 100Гц. После внесения изменений запустить модель и построить график сигнала на выходе ФАПЧ. По графику определить момент начала формирования сигнала с частотой 100Гц (момент захвата) и момент окончания формирования (момент срыва слежения). Зная скорость сканирования частоты Sweep-генератора и его начальную (конечную) частоту, определить полосу захвата и полосу удержания ФАПЧ.

СОДЕРЖАНИЕ ОТЧЕТА.

1. Наименование работы, ее цель и задачи.

2. Структурная схема моделей, их параметры, параметры системного времени.

3. Эскизы графиков сигналов, их спектров построения зависимости и вычисления значения параметров в соответствии с пунктом 1…4.

4. Выводы в соответствии с пунктами 1…4 «Хода выполнения работы».

ЛИТЕРАТУРА.

1. Шахгильдян В.В., ЛяховкинА.А. Системы фазовой автоподстройки частоты. М., Связь,1972, стр. 15-36, 80-84.

2. Гоноровский И.С. Радиотехнические цепи и сигналы. М. «Советское радио» 1977г. Стр 357-359.

ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ.

Объяснить на физическом уровне, почему ФАПЧ как управляемый генератор в установившемся режиме имеет нулевую ошибку отслеживания частоты задающего колебания.

ЛАБОРАТОРНАЯ РАБОТА №11

ИССЛЕДОВАНИЕ ОПТИМАЛЬНОГО ПРИЕМНИКА БИНАРНЫХ СИГНАЛОВ.

Цель работы: Исследовать свойства, характеристики и параметры оптимального приемника бинарных сигналов.

Задачи работы:

1. Изучить алгоритм обработки бинарных сигналов в оптимальном приемнике.

2. Изучить рабочие характеристики оптимального приемника.

3. Изучить влияние линии связи на работу оптимального приемника бинарных сигналов.

ВВЕДЕНИЕ.

Частным случаем дискретных сигналов являются сигналы бинарные, принимающие одно из двух возможных значений (0,1 или -1,+1). Прием бинарных сигналов в шумах является одной из важных проблем, решаемых в теории электросвязи. На решении этой проблемы основаны многие методы оптимальной обработки сигналов в цифровых системах связи.

Бинарный сигнал может быть представлен в виде

,

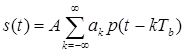где

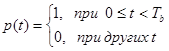, ступенчатая функция,

, длительность элементарной бинарной посылки сигнала,

, информационный параметр бинарного сигнала, представляющий в рассматриваемом случае последовательность значений ,

, амплитуда передаваемых импульсов.

Оптимальный приемник, структурная схема которого приведена на рис. 1, представляет собой устройство, осуществляющее когерентную обработку поступающей импульсной последовательности с использованием информации о моментах изменения передаваемого бинарного сигнала. Эта обработка включает интегрирование сигнала в течение времени и сравнении полученного результата интегрирования с заданным порогом. Входным сигналом приемника является аддитивная смесь

,

где - Гауссов белый шум.

Приемник оптимален в смысле минимума средней вероятности ошибочных решений, получаемых при обработке каждого поступающего на его вход информационного бита. Средняя вероятность ошибочного решения будет равна

,

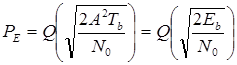где 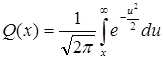- функция Гаусса,

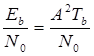- отношение энергии на бит к спектральной плотности шума.

Как видно из приведенной формулы, является только функцией от соотношения энергий на бит сигнала и шума. Эта зависимость является одной из разновидностей характеристик, используемых для оценки качества приема дискретных сигналов в шумах и называемых рабочими характеристиками приемника (РХП).

ПОСТАНОВКА ЗАДАЧ ИССЛЕДОВАНИЯ.

В данном исследовании работа оптимального приемника воспроизводится моделью, структура которой приведена на рис. 2. Источник 9 генерирует случайную бинарную последовательность , с которой смешивается Гауссов белый шум, поступающий от источника 1. Эта смесь обрабатывается модулем 10, осуществляющим скользящее усреднение на интервале . Дискретизация проинтегрированного сигнала по времени осуществляется модулем 11, сравнение с порогом - модулем 3. Модули 12 и 15 воспроизводят работу такого же приемника, но обрабатывающего импульсную последовательность без шумов, а, следовательно, и без ошибок при принятии решений. Этот приемник используется в качестве эталонного по отношению к исследуемому при оценке правильности принятия решений. Для получения оценок вероятности ошибочных решений в данной работе используется метод статистических испытаний (метод Монте-Карло), предусматривающий накопление и обработку статистических данных при обработке приемником, поступающей на его вход случайной бинарной последовательности . Результаты обработки каждого поступившего на вход приемника бита (принятое решение) оценивается на предмет правильности или ошибочности, суммируются с результатом предыдущих оценок и эта сумма делится на число обработанных бит. При неограниченном увеличении числа обрабатываемых бит, полученное отношение сходится по вероятности к соответствующей вероятности (в нашем случае - средней вероятности ошибочных решений). Процесс моделирования заканчивается при достижении заданного порогового числа анализируемых событий (в нашем случае - ошибок в принятии решений).

В данной работе предусматривается анализ процессов обработки сигналов в приемнике (на основе сопоставления графиков сигналов в нем с соответствующими графиками для эталонного приемника). Кроме того, планом работы предусмотрено экспериментальное получение РХП и сравнение ее с теоретической, исследование работы приемника при включении на его входе линии связи, вносящей задержку и ограничивающей спектр сигнала и шума, получение РХП для этих случаев.

ПЛАН ВЫПОЛНЕНИЯ РАБОТЫ.

1. Загрузить исполняющий файл com_bbb.svu (Рис.2). Войти в Help пакета, изучить функции и параметры модулей 3,4,5,6,7,9,10,11. Дать описание функций и параметров этих модулей.

2. Дополнить модель анализирующими модулями для регистрации выходных сигналов модулей 9, 11,12,15. Изменить частоту дискретизации при моделировании с 1 Гц на 10 Гц. Записать параметры модулей и системного времени.

3. Запустить модель на цикл моделирования и получить графики величин, характеризующих работу оптимального приемника при наличии и отсутствии помех. Для улучшения разрешения по времени необходимо изменить масштаб соответствующих анализирующих окон так, что бы на экран выводился отрезок реализации длиной 30-50с. Сравнить графики соответствующих величин для случая наличия помех и их отсутствия и дать объяснения отличиям.

4. Получить график сигнала на выходе модуля 3. Объяснить его формирование на основе анализа входных сигналов этого модуля и функции, реализуемой модулем.

5. Объяснить поведение кривых на графиках зависимостей, регистрируемых модулями 5 и 13. Дать объяснения величинам, представленных на этих графиках на момент окончания моделирования. Сравнить значения этих величин со значениями, выводимыми на транспаранты (Sink 5, Sink 13) структурной схемы модели.

6. Задавшись рядом значений спектральной плотности шума (5-6 точек в интервале 0.5-8 вт/Гц) и изменяя тем самым отношение энергии-на-бит к спектральной плотности шума , построить график вероятности ошибочного приема от величины этого отношения (РХП). Для повышения достоверности результатов необходимо увеличить максимальное число отсчетов при моделировании до 200000 (Sys. Time) и пороговое значение ошибок для окончания моделирования до 1000 (модуль 7). Оценить повторяемость результатов.

7. Получить спектр передаваемой импульсной последовательности. Установить на входе приемника (модуль 10) ФНЧ Бесселя 9-го порядка с частотой среза, соответствующей третьему минимуму в спектре передаваемого сигнала. Этот фильтр будет моделировать несовершенную линию связи, ограничивающую спектр сигнала. Определить вносимую фильтром задержку. Для ее компенсации на входе эталонного приемника (модуль 12) установить элемент задержки с необходимой величиной задержки.

8. Выполнить п.2 «Плана выполнения работы».

9. Выполнить п.6 «Плана выполнения работы» и сравнить полученные результаты с результатами п.8. Дать обоснование наблюдаемым различиям.

10. Построить график теоретической РХП, вычисленной для использованных в п.6 значений спектральной плотности шума. Сравнить полученный график с результатами п.6.

СОДЕРЖАНИЕ ОТЧЕТА.

1. Наименование работы, ее цель и задачи.

2. Структурная схема моделей, их параметры, параметры системного времени.

3. Эскизы графиков сигналов, их спектров построения зависимости и

вычисления значения параметров в соответствии с пунктом 1-10 Плана выполнения работы.

4. Выводы в соответствии с пунктами 1-10 Плана выполнения работы.

ЛИТЕРАТУРА.

1. Фельдбаум А. .А. и др. Теоретические основы связи и управления.

2. Зюко А.Г. и др. Теория передачи сигналов.

ДОПОЛНИТЕЛЬНОЕ ЗАДАНИЕ.

Предложить и обосновать структурную схему модели для исследования влияния энергии шума на вероятности ложного приема 1 и пропуска 1 (Вероятности ошибок типа ложная тревога и пропуск сигнала) при приеме дискретных сигналов оптимальным приемником.

Скачать архив с текстом документа