Методические указания по изучению дисциплины Действительный анализ для студентов специальности 050601 Математика
СОДЕРЖАНИЕ: Рабочая программа разработана на основании Государственного общеобязательного стандарта специальности госо рк 08. 321-2006 и типовой программы дисциплин по специальности 050601 «Математика», утвержденной румс от 22. 06. 2006г| Титульный лист Методических рекомендаций и указаний; методических рекомендаций; методических указаний |
|
Форма СО ПГУ 7.18.3/40 |
Министерство образования и науки Республики Казахстан
Павлодарский государственный университет им. С. Торайгырова
Кафедра математики
методические указания
по изучению дисциплины
Действительный анализ
для студентов специальности 050601 Математика
Павлодар
| Лист утверждения лист методических рекомендаций и указаний; методических рекомендаций; методических указаний |
|
Форма СО ПГУ 7.18.3/41 |
УТВЕРЖДАЮ
Проректор по УР
___________________Пфейфер Н.Э.
«__»_______________20___г.
Составитель: к.ф.-м.н., профессор ПГУ им. С.Торайгырова Муканов Г.М.
Кафедра математики
Методические указания по изучению дисциплины
Действительный анализ
для студентов специальности 050601 «Математика»
Рабочая программа разработана на основании Государственного общеобязательного стандарта специальности ГОСО РК 3.08.321-2006 и типовой программы дисциплин по специальности 050601 «Математика», утвержденной РУМС от 22.06.2006г.
Рекомендована на заседании кафедры «____»________20__ г. Протокол №____
Заведующий кафедрой _______________И.И. Павлюк «____»________20__ г.
Одобрена УМС факультета физики, математики и информационных технологий
«___»___________20__г. Протокол №______
Председатель УМС______________ Ж.Г. Муканова «____»________20__ г.
ОДОБРЕНО
Начальник ОПиМО ______________А.А.Варакута «____»________20__г.
Содержание теоретического курса
Тема 1 Множества
Лекция №1. Примеры множества различной природы. Числовые множества N, Z , Q, I, R . Операции над множествами. Функции на множествах, взаимно однозначные отображения. Эквивалентные множества. Мощность множества. Конечные, счетные множества.
Лекция №2. Множества мощности континуума. Теоремы о счетных и континуальных множествах. Сравнение мощностей. Теорема Кантора-Бернштейна.
Содержание практических занятий
Занятие №1. Примеры множеств различной природы. Операции над множествами.
Вопросы, подлежащие освоению:
* понятие множества (на примерах N, Z, Q, I, R и другие);
* операции над множествами.
* Решение примеров. [8] 1 – 25 (решить 5, 6 примеров по выбору);
Литература [1], 17 – 21.
Занятие №2 . Функции па множествах
Вопросы, подлежащие освоению:
* взаимно однозначное отображение;
* эквивалентные множества;.
* Решение примеров. [8] 27 – 44 (решить 5, 6 примеров по выбору );
Литература [1], 21 – 26.
Занятие №3 . Мощность множества
Вопросы, подлежащие освоению:
* понятие мощности множества;
* конечная мощность;
* счетная мощность;
* свойства счетной мощности;
* Решение примеров. [8] 61 – 68 (решить 5, 6 примеров пл выбору);
Литература [1], 26 – 30.
Занятие №4 . Сравнение мощностей
Вопросы, подлежащие освоению:
* множество мощности континуума;
* сравнение мощностей (определение нонятий: «больше», «меньше» и «равно» между мощностями);
* доказательство того, что мощность континуума больше счетной мощности;
* теорема Кантора-Бернштейна;
* теорема о неограниченности совокупности всех мощностей;
* континуум - гипотеза Кантора
* Решение примеров. [8] 27 – 44 (решить 5, 6 примеров по выбору.);
Литература [1], 30 – 34.
Тема 2 Топологические классы множеств.
Лекция №3. Открытые и замкнутые множества, их объединения и пересечения. Строение открытых и замкнутых множеств во множестве R действительных чисел и их строение.
Лекция №4. Множества всюду плотные и нигде неплотные на данном множестве. Совершенное множество. Канторовы открытое и совершенное множество.
Содержание практических занятий
Занятие №5
Вопросы, подлежащие освоению:
* основные типы точек (точка прикосновения, предельная точка, точка еонденсеции, изолированная точка, внутренняя точка, внешняя точка, граничная точка);
* окрестность точки числовой прямой;
* основные типы множеств (открвтые, замкнутые, всюду плотные, плотные в себе, совершенные);
* Канторово совершенное множество ![]() , его мощность.
, его мощность.
* Решение примеров. [8] 225.
Литература [1], 67 – 78, 288 – 303.
Занятие №6
Вопросы, подлежащие освоению:
* Канторово открытое множество Р как дополнение Каторово совершенного множества Р0 до сегмента [0,1]
* Структура ограниченного открытого, Замкнутого и совнршенного множества.
* Решение примеров. [8] 213 - 216.
Литература [1], 288 – 303.
Занятие №7
Вопросы, подлежащие освоению:
* всюду плотные множества;
* нигде неплотные множества;
* нигде неплотность канторова совершенного множества.
* Решение примеров. [8] 217 – 220.
Литература [1], 288 – 323
Занятие №8
Вопросы, подлежащие освоению:
* Арифметическая структура канторво совершенного множества.
* Решение примеров. [8] 225 – 230.
Литература [1], 288 – 323.
Тема 3 Мера множества
Лекция №5. Мера открытых множеств, ее аддитивное свойство. Внешняя мера на R, ее монотонность и счетная полуаддитивность. Определение меры Лебега для числовых множеств. Множество меры нуль и связанные с ним свойства. Примеры простейших измеримых множеств.
Лекция №6. Измеримость множества по Каратеодори. Эквивалентность различных определений измеримости множества. Доказательство замкнутости системы всех измеримых множеств относительно конечных и счетных операций.
Содержание практических занятий
Занятие №9
Вопросы, подлежащие освоению:
* мера открытых множеств;
* аддитивность меры открытого множества;
* Внешняя мера на R;
* счетная полуаддитивность внешней меры;
* Решение примеров. [8] 408 – 411.
Литература [1], 288 – 323.
Занятие №10
Вопросы, подлежащие освоению:
* определение меры Лебега для числовых множеств;
* множество меры нуль и связанные с ним свойства;
* примеры простейших измеримых множеств;
* Решение примеров. [8] 416 – 418.
Литература [1], 288 – 323.
Занятие №11
Вопросы, подлежащие освоению:
* измеримость множеств по Каратеодори;
* Эквивалентность различнвх определений измеримости множеств.
* Решение примеров. [8] 419, 420.
Литература [1], 323 – 334.
Занятие №12
Вопросы, подлежащие освоению:
* Доказательство замкнутости системы всех измеримых множеств относительно конечных и счетных операций.
* Решение примеров. [8] 421 – 425. Литература [1], 323 – 334.
Тема 4 Измеримые функции
Лекция №7. Определение и простейшие примкры измеримых функций. Измеримость суммы, пройзведения и частного измеримых функций. Сходимость почти всюду и по мере последовательности измеримых функций. Измеримость предела последовательности, сходящейся почти всюду.
Лекция №8. Основные виды сходимостей (всюду, равномерная, почти всюду и по мере) и их сравнение.
Содержание практических занятий
Занятие №13
Вопросы, подлежащие освоению:
* определение измеримой функции;
* измеримость суммы измеримых функций;
* пройзведения и частного измеримых функций.
* Решение примеров. [8] 679 – 685.
Литература [1], 323 – 334.
Занятие №14
Вопросы, подлежащие освоению:
* сходимость последовательности почти всюду;
* сходимость последовательности по мере;
* сходимость последоательности всюду;
* равномерная сходимость последовательности;
* Решение примеров. [8] 696, 699.
Литература [1], 323 – 334.
Занятие №15
Вопросы, подлежащие освоению:
* измеримость предела последовательности, сходящейися почти всюду.
* сравнение сходимости по мере со сходимостию почти всюду (теорема Лебнга, пример Рисса, теорема Рисса).
* Решение примеров № 699, 700.
Литература [1], 323 – 334.
Занятие №16
Вопросы, подлежащие освоению:
* сравнение сходимости пости вюду с равномерной сходимостью (т. Егорова Д.Ф.);
* сруктура измеримой функции (т. Лузина Н.Н., или С-свойство).
Литература [1], 323 – 334.
Тема 5 Интеграл Лебега
Лекция №9. Определение интеграла Лебега от ограниченной функции на множестве конечной меры и его существование. Основные свойства. Теорема Лебега о предельном переходе под знаком интеграла Лебега. Сравнение интеграла Лебега с интегралом Римана.
Лекция №10.. Функций ограниченной вариации и их свойства. Абсолютно непрерывные функции и их свойства
Лекция №11. Мера Лебега-Стилтьеса. Интегралы Лебега-Стилтьеса и Римана-Стилтьеса.
Содержание практических занятий
Занятие №17
Вопросы, подлежащие освоению:
* определение интеграла Лебега от ограниченной функции;
* основные свойства интеграла Лебега;
* Решение примеров. [8] 710, 709, 710.
Литература [1], 334 – 355.
Занятие №18
Вопросы, подлежащие освоению:
* существование интеграла Лебега от измеримой ограничнной функции;
* Решение примеров. [8] 713, 714.
Литература [1], 334 – 355.
Занятие №19
Вопросы, подлежащие освоению:
* сравнение интегала Лебега с интегралом Римана.
* Решение примеров. [8] Решить примеры: № 715 – 718
Литература [1], 334 – 355.
Занятие №20
Вопросы, подлежащие освоению:
* интеграл Лебега от неотрицательной измеримой функции;
* суммируемые функции любого знака.
* Решение примеров. [8] 719, 723 – 725.
Литература [1], 334 – 355.
Занятие №21
Вопросы, подлежащие освоению:
* предельный переход под знаком интеграла Лебега.
* Решение примеров. [8] 732 – 735.
Литература [1], 334 – 355.
Занятие №22
Вопросы, подлежащие освоению:
* функции с ограниченным иизменением;
* мера Лебега-Стилтьеса;
* интеграл Лебега-Стилтьеса;
* интеграл Римана-Стилтьеса.
* Решение примеров. [8] 736, 745, 746.
Литература [1], 368 – 423.
Тема 6 Восстановление функции по ее производной
Лекция №12. Абсолютная непрерывность неопределенного интеграла Лебега. Теорема Лебега о восстановлении абсолютно непрерывной функции по ее пройзводной. Граница применимости формулы Ньютона-Лейбница.
Содержание практических занятий
Занятие №23
Вопросы, подлежащие освоению:
* представимость монотонной функции как разность двух монотонно неубыващих функции;
* абсолютно непрерывная функция;
* функция скачков;
* сингулярная функция;
* представимлсть функции с ограниченным изменением в виде суммы трех компанент – функции скачков, абсолютно непрерывной функции и сингулярной функции.
Литература [1], 368 – 423.
Занятие №24
Вопросы, подлежащие освоению:
* восстановление функции по ее производной;
* граница применимости формулы Ньютона-Лейбница.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 368 – 423.
Тема 7 Классы функции
Занятие №25
Вопросы, подлежащие освоению:
* класс интегрируемых по Лебегу функций;
* классы функций Лебега 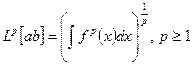 ;
;
* сходимость последовательности суммируемых по Лебегу функций в среднем;
* сравнение сходимости в среднем со сходимостью по мере.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 368 – 423.
Занятие №26
Вопросы, подлежащие освоению:
* сходимость в классе функций с суммируемым квадратом;
* сравнение сходимости в среднеквадратическом с другими видами сходимости.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 368 – 423.
Занятие №27
Вопросы, подлежащие освоению:
* тригонометрическая система функций;
* коэффициенты Фурье функции с суммируемым квадратом;
* ряд Фурье функции с суммируемым квадратом.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 368 – 423.
Занятие №28
Вопросы, подлежащие освоению:
* примеры на разложение функции в ряд Фурье.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 368 – 423.
Тема 7 Классы функций
Лекция №13. Класс суммируемых по Лебегу функций. Шкала лебеговских классов. Сходимость последовательности измеримых функций в среднем.
Лекция №14. Сравнение сходимости в среднем с другими видами сходимостей. Класс функций, суммируемых в среднем квадратическом.
Тема 8 Мера и интеграл Лебега в пространстве
![]()
Лекция №15. Функции многих переменных, определенные на множествах конечномерного действительного пространства. Произведение линейных мер. Суммируемые функции многих переменных. Теорема Фубини.
Содержание практических занятий
Занятие №29
Вопросы, подлежащие освоению:
* функции, определенные на множествах пространства Rn ;
* произведение линейных мер;
* определение кратного интеграла.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 355 –363.
Занятие №30
Вопросы, подлежащие освоению:
* суммируемые функции многих переменных;
* теорема Фубини.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 355 – 363.
Литература
Основная:
1. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М: Наука, 1989.
2. Натансон И.П. Терия функций вещественной переменной. М: Наука, 1974.
3. Дьяченко М.И. , Ульянов П.П. Мера и интеграл. М: Факторная, 1998.
4. Теміргалиев Н. Математикалы анализ, т.2. Алматы: Ана тілі, 1991.
5. Лузин Н.Н. Теория функций действительного переменного . - М.: ГУНИ,
6. Брудно А.Л. Теория функций действительного переменного . - М.: Наука, 1971.
7. Толстов Г.П. Мера и интеграл. – М.: Наука, 1976.
8. Очан Ю.С. Сборник задач по математическому анализу. М. 1981.
9. Теляковский С.А. Сборник задач по теории функций действительного переменного. М: Наука, 1980.
Дополнительная:
10. Александров П.С. ВВедение в теорию множеств и общую топологию.М,1977.
11. Хаусдорф Ф. Терия множеств. М. ОНТИ, 1937.
12. Халмош П. Теория меры. М: ИЛ, 1953.
13. Сахс С. Теория интеграла. М.: ИЛ, 1949.
14. Рудин У. Основы математическогго анлиза. М. : Мир, 1966.
15. Лузин Н.Н. Интеграл и тригонометрический ряд . М.: ГИТТЛ, 1951.
16. Камне Е. Интеграл Лебега- Стилтьеса. М.: Физматгиз, 1959.
17. . М. Манов, Наты айнымалы функциялар теориясыны негіздері.

