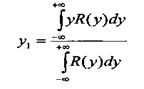Методические указания по лабораторным работам Факультет: электроэнергетический

СОДЕРЖАНИЕ: Моделирование: методические указания по лабораторным работам. Вологда: Вогту, 2003. 35 с

Министерство образования Российской Ф едерации

ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра управляющих и вычислительных систем

МОДЕЛИРОВАНИЕ

Методические указания

по лабораторным работам

Факультет: электроэнергетический

Специальность: 220100 -вычислительные машины,

комплексы, системы и сети

Вологда 2003

УДК 681.5

Моделирование: методические указания по лабораторным работам. - Вологда: ВоГТУ, 2003. 35 с.

Представленные методические указания по лабораторному практикуму соответствуют рабочей программе курса «Моделирование» и предназначены для студентов дневного отделения специальности 220100 -вычислительные машины, комплексы, системы и сети

Утверждено редакционно-издательским советом ВоГТУ

Составитель: В.Н. Бакаев, канд. техн. наук, доцент.

Рецензент: В.А. Горбунов, канд. физ-.мат. наук, до-

цент.

ЛАБОРАТОРНАЯ РАБОТА № 1

Исследование системы с нечетким управлением

Цель работы: получение практических навыков работы с нечетким регулятором.

Задание на лабораторную работу: разработать систему нечетких правил и функций принадлежности для управления автомобилем на перекрестке [12].

При этом:

1. Автомобиль должен двигаться со скоростью не ниже 60 км/ч по улице вдали от светофора.

2. Автомобиль должен останавливаться на перекрестке на красный сигнал светофора.

3. Режим работы светофора в зависимости от варианта:

Вариант Режим работы светофора

1 красный, красный и желтый, зеленый, желтый...

2 красный, красный и желтый, зеленый, желтый...

А также светофор может не работать.

3 красный, желтый, зеленый, желтый...

4 красный, красный и желтый, зеленый, желтый...

А также светофор может мелькать желтым.

5 красный, красный и желтый, зеленый, желтый...

А также светофор может не работать и мелькать желтым.

6 красный, красный и желтый, зеленый, желтый...

Сигнала с системы технического зрения не всегда на 100%

достоверен.

7 красный, красный и желтый, зеленый, желтый...

А также светофор может не работать. Сигнал с системы

технического зрения не всегда на 100% достоверен.

Если светофор мелькает желтым (варианты 5 и 6), то автомобиль должен проезжать перекресток со скоростью ниже 40 км/ч.

При нарушении правил автомобиль попадает в аварию. При этом Вы можете увидеть соответствующую анимацию.

Ниже приведена таблица состояния флагов опций для каждого варианта:

Таблица 1.

Состояние флагов опций для различных вариантов.

1 2 3 4 5 6 7

Светофор | Может не работать * * *

Светофор | Может мелькать желтым * *

Светофор | Красный и желтый * * * * * *

Автомобиль | 100% дост-сть датчиков * * * * *

Описание функциональной схемы автомобиля

Система управления автомобилем состоит из следующих блоков (Рис.1): телекамера, система технического зрения, нечеткий регулятор, система управления скоростью, исполнительная часть автомобиля. При этом все блоки, кроме нечеткого регулятора, мы будем рассматривать, как черный ящик.

Система технического зрения обрабатывает видеоизображения, получаемые с телекамеры. При обработке изображения распознается образ светофора. На выходе системы формируется сигнал расстояния до светофора (X) и сигнал света светофора (С).

Система управления автомобилем

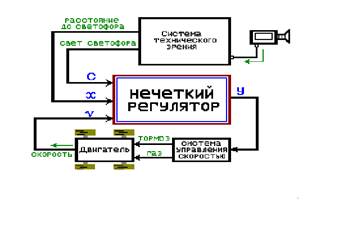
Рис.1

Эти сигналы совместно с сигналом спидометра автомобиля (V) поступают в нечеткий регулятор. В данной работе Вам предложено научить нечеткий регулятор обрабатывать эти сигналы. На выходе нечеткого регулятора нужно сформировать сигнал уставки на скорость (Y).

Сигнал уставки поступает на систему управления скоростью, а оттуда на исполнительную часть автомобиля.

В упрощенном варианте система технического зрения выдает достоверную информацию о сигнале светофора. Эта информация поступает в нечеткий регулятор в виде входной переменной С. Причем при красном сигнале светофора значение переменной С равно 0. При сигнале красный и желтый значение С=1. При зеленом С=2. И т.д. (см. таблицу 2).

Таблица 2.

Значение переменной С при различном состоянии светофора.

Состояние светофора Значение С

Красный О

Красный и желтый 1

Зеленый 2

Желтый 3

Желтый мерцает 4

Не работает 5

В вариантах 6 и 7 система технического зрения выдает недостоверный сигнал. В этом случае значение переменной С принимает не дискретное, а непрерывное значение. Т.е. при зеленом сигнале светофора значение С может составлять, например, 2.25. Это значит, что система технического зрения видит на светофоре зеленый свет с определенной долей вероятности. По умолчанию функции принадлежности по переменной С составлены так, что значение 2.25 к понятию зеленый будет относиться с достоверностью 0.5.

Сигнал расстояния до светофора (X) измеряется в метрах. Если светофор не найден или расстояние до него свыше 140 м., то значение этого сигнала равно 140 м. Сигнал со спидометра (V) и сигнал уставки (Y) измеряются в км/ч.

Порядок выполнения работы

1. Согласно варианту установите соответствующие опции.

2. Выберите пункт меню Задача | Новая задача или нажмите на соответствующую кнопку на панели инструментов.

3. Задайте функции принадлежности и правила (см. Как задать функции принадлежности, а также Как задать правила).

4. Запустите процесс. Для этого выберите пункт меню Задача Работа или выставите соответствующий флажок на панели инструментов. Также Вы можете воспользоваться отладчиком. Для этого выберите пункт меню Fuzzy | Отладка или нажмите F8.

5. Для перезапуска эксперимента (например, после аварии) выберите пункт меню Задача Перезапуск или нажмите Ctrl-F2.

6. Для изменения функций принадлежности или правил выберите пункт меню Fuzzy Изменить или двойным щелчком щелкните по рабочему полю окна.

7. Повторите пункты 3-6, пока не получите наилучший, на Ваш взгляд, результат.

Как начать новый проект

Чтобы начать новый проект выберите пункт меню Задача | Новая задача.

Откроется окно Нечеткий регулятор, в котором следует задать систему нечетких правил и функций принадлежности.

Как задать функции принадлежности

Откройте окно Нечеткий регулятор и выберите страничку Функции принадлежности.

Перед Вами графический редактор функций принадлежности.

Чтобы задать новую функцию принадлежности, нажмите кнопку Добавить из группы функции. В появившемся окне наберите имя новой функции и выберите ее аргумент.

Для того, чтобы изменить имеющуюся функцию принадлежности, выберите ее в списке функции.

Редактирование функции заключается в рисовании ее графика. Для этого Вам предложено 4 инструмента: Карандаш, Перенос точки, Вставка точки, разбив линию, Удаление точки. Редактирование возможно только выбранной функции принадлежности, (см. Как составляются функции принадлежности).

Имена функций принадлежности пишутся непосредственно над их графиками.

Функции принадлежности можно удалять (кнопка Удалить из группы функции), копировать в буфер обмена (кнопка Копировать), вставлять из буфера обмена (кнопка Вставить), а также переименовывать (кнопка Смена имя).

Функции принадлежности по переменной С жестко заданы и их изменять смысла не имеет. Однако, при необходимости можно получить к ним доступ, сняв с них флажок только для чтения.

Как задать нечеткие правила

Откройте окно Нечеткий регулятор и выберите страничку Правила.

В появившемся редакторе необходимо записать систему нечетких правил в виде текста, (см. Как составляются нечеткие правила).

Для удобства Вы можете воспользоваться макротекстом. Под полем редактора имеются списки из зарезервированных слов, имен переменных и функций принадлежности.

Для проверки ошибок в написании нажмите кнопку Проверить.

Если есть необходимость сохранить правила в текстовый файл или загрузить правила из него, необходимо щелкнуть правой клавишей мыши по редактору и выбрать в всплывающем меню соответственно пункт Сохранить правила или Загрузить правила.

Как выбрать метод деффазификации

Чтобы выбрать метод деффазификации (см. Как работает нечеткий регулятор) откройте окно Нечеткий регулятор и выберите соответствующий метод в группе Метод.

Как запустить/перезапустить эксперимент

Для того чтобы запустить эксперимент, выберите пункт меню Задача | Перезапустить.

Если же необходимо остановить/запустить время, выставьте/снимите галочку с пункта меню Задача Работа или выставьте/снимите соответствующий флажок на панели инструментов.

Как открыть окно Нечеткий регулятор снова

Для того чтобы открыть окно Нечеткий регулятор , выберите пункт меню Fuzzy | Изменить или нажмите соответствующую кнопку на панели инструментов или двойным щелчком щелкните по полю окна.

Как пользоваться отладчиком

Для запуска отладчика, выберите пункт меню Fuzzy Отладка или нажмите соответствующую кнопку на панели инструментов или просто нажмите F8.

Появится окно Отладчик. В нем Вы можете увидеть систему нечетких правил и функций принадлежностей, набранных Вами (функции принадлежности не именуются).

Дальнейшее нажатие F8 будет выполнять нечеткие правила по шагам. При этом Вы можете наблюдать текущее значение всех переменных.

Вы можете изменять их значение, путем перемещения мышкой вертикальной черты на графиках функций принадлежности.

Также Вы можете видеть последнее значение оценки достоверности (Ak) (см. Как работает нечеткий регулятор).

Кроме того, результирующая фигура также отображается на графиках (см. Как работает нечеткий регулятор).

Как сохранить или загрузить результаты

Для того чтобы сохранить/загрузить результаты проделанной работы, откройте окно Нечеткий регулятор и нажмите соответственно кнопку Сохранить или Загрузить.

Как составляются функции принадлежности

Функции принадлежности составляются по каждой входной и выходной переменной. В данной работе нечеткий регуля-

тор имеет три входные переменные (с - свет светофора, х - расстояние до светофора, v -текущая скорость автомобиля) и одну выходную переменную (у - уставка на скорость для системы управления автомобилем).

А) Функции принадлежности по входным переменным

Для составления функций принадлежности необходимо разбить всю область допустимых значений по каждой входной переменной на конечное число характеристик, называемых термами. Например, для скорости v можно сказать: медленно, средне, быстро и т.д.

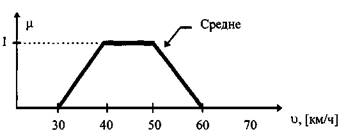
Затем следует составить функции принадлежности к каждому терму. Т.е. составить график, показывающий с какой долей уверенности можно отнести то или иное значение переменной к тому или иному терму. Например:

Скорости 40-50 км/ч можно смело отнести к понятию средне, т.к. степень достоверности по данному графику для этого значения скоростей равняется 1. Скорость 35 км/ч и 55 км/ч относится к понятию средне со степенью достоверности ~0.5. Скорости вне диапазона 30-60 км/ч к понятию средне не относятся. То же само для остальных термов (быстро, медленно и т.д.).

Следует отметить, что функции принадлежности должны иметь максимум, равный 1. Все значения функции принадлежности должны лежать в пределах [0,1]. Функция принадлежности может быть не только трапецеидальной формы, но и любой другой. Практически ни в одной литературе не приводятся рекомендации о форме функций принадлежности, но наиболее распространены прямоугольные, треугольные, трапецеидальные формы, а также в виде функции нормального распределения.

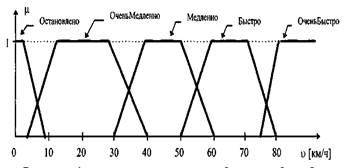
Полный набор функций принадлежности по переменной можно, например, представить так:

Для введения функции принадлежности в данной лабораторной работе выберите пункт меню Fuzzy | Изменить или нажмите соответствующую кнопку на панели инструментов.

Б) Функции принадлежности по выходной переменной

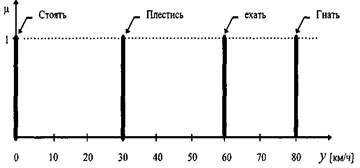
Также, как и для входной переменной, весь диапазон значений выходной переменной следует разбить на конечное число термов. В нашем случае выходная переменная у есть уставка на скорость. Ее можно характеризовать как: Медленно, Средне, Быстро и т.д. Но, чтобы не повторять имена функций принадлежности, назовем их так: Плестись, Ехать, Гнать и т.д.

Составляются функции принадлежности точно так же, как и по входным переменным. Однако часто выходные функции принадлежности делают вырожденными:

Как составляются правила

Нечеткие правила составляются на основе конструкции Если ... то ..... Т.е., например:

Если Свет есть Зеленый, то Скорость есть Быстро. Здесь:

Свет - входная переменная.

Скорость - выходная переменная.

Зеленый - функция принадлежности по переменной Свет.

Быстро - функция принадлежности по переменной Скорость.

Нечеткий регулятор оперирует с нечеткой информацией. Поэтому достоверность конструкции если... не всегда равна 0 или 1, как в булевой алгебре, а может принимать и промежуточные значения из интервала [0,1]. Это обстоятельство соответствующим образом учитывается в конструкции то..., (см. Как работает нечеткий регулятор).

В данной работе нечеткие правила записываются в виде текста и имеют следующий формат:

IF [NOТ]вх.переменная IS функция [знак [NOT] вх.переменная IS функция[...]] THEN вых.переменная IS функция [AND вых.переменная[...]]

где:

вх.переменная - входная переменная.

вых.переменная - выходная переменная.

функция - функция принадлежности.

знак - AND или OR соответственно И или ИЛИ

Пример:

IF с is Зеленый and x is Близко then у is Гнать

IF с is Красный and x is Близко then у is Стоять

IF x is Недалеко and (с is Красный or с is Желтый) then у is Стоять

IF v is ОченьБыстро and с is Желтый and x is Близко then у is Быстро

IF not v is Быстро and not (c is Желтый or с is КрасЖел) then у is Медленно

Нечеткий регулятор обычно содержит несколько нечетких правил. Каждое нечеткое правило должно быть записано в одну строчку. Для задания нечетких правил в данной лабораторной работе выберите пункт меню Fuzzy | Изменить или нажмите соответствующую кнопку на панели инструментов.

Как работает нечеткий регулятор

Процесс работы нечеткого регулятора можно наглядно представить увидеть в окне отладчика. Рассмотрим алгоритм работы нечеткого регулятора на примере.

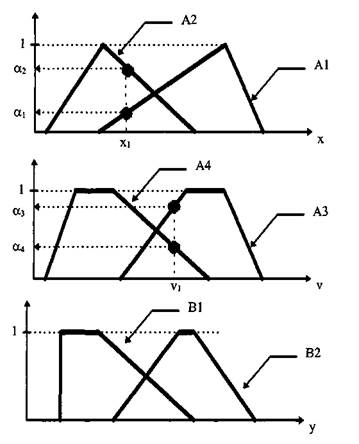
Пусть нечеткий регулятор имеет две входные переменные (х, v) и одну выходную (у), функции принадлежности по которым представлены ниже.

Пусть в данный момент времени значение переменной х будет хь а переменной v - будет v1 .

Пусть нечеткие правила выглядят так:

IF not х is Al and v is A3 then у is Bl

IF x is A2 or v is A4 then у is B2

Следуя первому правилу, нечеткий регулятор выполнит следующее:

1. Оценит степень достоверности выражения х is Al. Достоверность этого выражения есть значение функции Al(xt ). В нашем случае А1(х1 )= a1 . Этот процесс называется фаззификацией.

2. Оценит степень достоверности выражения v is A3. Достоверность этого выражения есть значение функции A3(v). В нашем случае это значение равно a3 .


3. Перед выражением х is Al стоит связка NOT. Это значит, что степень достоверности выражения not x is Al нечеткий регулятор будет считать как:

4. Далее нечеткий регулятор вычислит степень достоверности всего выражения not x is Al and v is A3.

Т.к. стоит связка AND, ищется минимум из a3 : aк =min(, a3 ).

Если бы была связка OR, искался максимум из a3 : aк =max(, a3 ).

Дальнейшие действия нечеткого регулятора зависят от метода нечеткого вывода. Известно два основных метода: MAX-МIN(усечение), МАХ-DОТ(масштабирование).

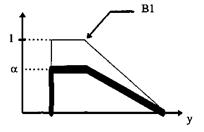
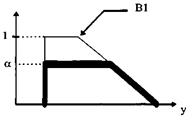
5. Выходная функция принадлеж- 5. Выходная функция принадлеж- ности (В1), стоящая в правиле, ности (В1), стоящая в правиле,

усекается значением , масштабируется значением,



полученным в п.4 полученным в п.4

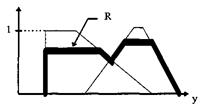
6. Результирующие фигуры, получаемые при выполнении правил, накладываются друг на друга (объединяются множества), образуя результирующую фигуру.


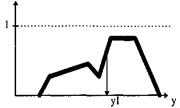
7. Далее нечеткий регулятор определяет значение выходной переменной путем поиска центра масс результирующей фигуры.

Данный процесс называется дефаззификацией. Поиск центра масс осуществляется по формуле:

Здесь: R(y) - результирующая фигура; y1 - получаемое значение выходной переменной в данный момент времени.

Следует отметить, что в общем случае результаты, полученные методами MAX-DOT и MAX-MIN, могут отличаться.

ЛАБОРАТОРНАЯ РАБОТА № 2

Исследование САУ с комбинированным

управлением

Цель работы: на основе математического моделирования оценить возможности САУ с комбинированным способом управления.

Задание на лабораторную работу: для привода руки робота используется реверсивный, замкнутый по скорости электропривод постоянного тока по системе ТП-ДПТ. Регулирование скорости двигателя постоянного тока (ДПТ) осуществляется изменением напряжения на якоре. Плавный разгон до номинальной скорости осуществляется с использованием задатчика интенсивности. Для компенсации скоростной ошибки применено комбинированное управление с передаточной функцией Wку (p)=b, охватывающее промежуточный усилитель Ку и регулятор скорости. Структурная схема изображена на рис. 2.

Передаточные функции двигателя и тиристорного преобразователя принять в виде:

Wтп (р)=Ктп /(Tтп р +1); Wдпт (р)=w(р)/Uд (р)=Кд /(Tя Tм р2 + Тм р +1);

Wдпт (р)=w(р)/Мс (р)= - Rя (Tя р +1) /(СеФ)2 (Tя Tм р2 + Тм р +1).

Структурная схема электропривода

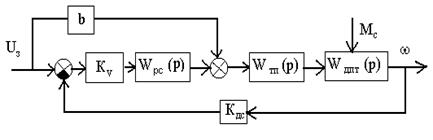Рис.2

Требуется:

1. Рассчитать величину Кдс , чтобы напряжение задания Uз для получения номинальной скорости не превышало 10В;

2. Настроить электропривод на модульный (технический) оптимум с использованием ПИ- или ПИД-регулятора. Построить л.а.х. и л.ф.х. разомкнутой скорректированной системы. Рассчитать параметры регулятора;

3. Рассчитать коэффициент компенсации b, обеспечивающий астатизм второго порядка по управлению;

4. Рассчитать величину постоянной заводки задатчика интенсивности, позволяющего плавно разгонять нагруженный электропривод с максимально-допустимым динамическим моментом. При этом принять Мс =Мн . ;

5. Определить установившееся значение скоростной ошибки, если момент нагрузки изменяется по закону Мс = 2t ;

6. Разработать математическую модель системы и, используя любой математический пакет прикладных программ, составить схему для исследования;

7. Провести экспериментальные исследования с использованием ЭВМ по п.п. 15.

Порядок выполнения работы

Параметры тиристорного преобразователя и элемента сравнения: Ктп = 8; Tтп =0,002; Ку = 4; двигатель выбирается согласно № по списку группы (см.Таблицу 3);

Таблица 3

Технические данные электродвигателей постоянного тока

№ Варианта ( по списку в журнале гр.)

Тип двигателя

Мощность РД НОМ , кВт

Напряжение UН , В

Скорость вращения nН , об/мин

Ток IН , А

К. П. Д. h, %

Маховый момент GD2 , кГ м2

Сопротивление обмоток при 20° С, Ом

Число главных полюсов 2р

Якоря rа , Ом

Добавочных полюсов rдп , Ом

Последовательного возбуждения или компенсационной rК , Ом

1

2

3

4

5

6

7

8

9

10

11

12

1 ДП-21

4,5

220

1050

26

78,5

0,5

0,66

0,28

—

4

2 ДП-22

6

220

1130

33

82,5

8,62

0,37

0,196

—

4

3 ДП-31

8,5

220

870

47

82,5

1,2

0,325

0,098

—

4

4 ДП-32

12

220

790

65

84

1,7

0,19

0,076

—

4

5 ДП-41

16

220

710

85

86

3,2

0,11

0,057

—

4

6 ДП-42

21

220

660

110

83

4,2

0,0725

0,043

—

4

7 ДП-42

29

440

1040

75

84

4,2

0,132

0,08

—

4

8 ДП-52

32

220

760

164

86

7,5

0,033

0,0215

—

4

9 П42

4,5

220

1500

25,4

90,5

0,18

0,545

0,235

0,0392

4

10 П51

6

220

1500

33,2

82

0,35

0,34

0,132

0,00736

4

11 П52

8

220

1500

43,5

84

0,4

0,185

0,084

0,0068

4

12 П61

11

220

1500

59,5

84

0,56

0,135

0,052

0,006

4

13 П62

14

220

1500

73,5

86,5

0,65

0,0875

0,04

0,004

4

14 П71

19

110

1500

210

82,5

1,4

0,0234

0,0079

0,00098

4

15 П71

19

220

1500

103

84

1,4

0,0912

0,0323

0,00486

4

16 П72

25

220

1500

132

86

1,6

0,0585

0,024

0,00432

4

17 П81

32

220

1500

116

87,5

2,7

0,057

0,018

0,0026

4

18 П82

25

440

1000

66

85,5

3,1

0,27

0,0948

0,00796

4

19 П82

42

220

1500

218

87,5

3,1

0,0263

0,00957

0,00079

4

20 П82

42

440

1500

107

89

3,1

0,105

0,0383

0,00216

4

21 П91

25

110

750

279

81,5

5,9

0,01875

0,0069

0,00102

4

22 П91

55

440

1500

143

87,5

5,9

0,0748

0,0275

0,00407

4

23 П92

42

440

1000

110

87

7,0

0,161

0,0544

0,0048

4

24 П101

42

110

750

446

85,5

10,3

0,00864

0,00323

0,00034

4

Продолжение табл.

1

2

3

4

5

6

7

8

9

10

11

12

25 П20-30-7К

1750

630

330

2970

93,5

13600

0,00396

0,000429

0,00258

8

26 П19-50-7к

1750

630

370

2950

94,2

12500

0,00332

0,000517

0,00188

8

27 П19-50-7к

2100

750

350

2970

94,1

14000

0,00389

0,000607

0,00201

8

28 П20-40-7к

2400

860

350

2970

94,1

16100

0,00428

0,00052

0,00276

8

29 П19-45-7к

2400

860

450

2950

94,6

14500

0,00345

0,000563

0,001945

8

30 П20-35-7к

2800

1000

450

2965

94,4

14 900

0,00411

0,000475

0,00267

8

31 П20-30-7К

2800

1000

530

2960

94,5

13600

0,00396

0,000429

0,00258

8

32 П21-35-5к

3300

630

310

5540

94,2

30120

0,00138

0,000174

0,001027

10

33 П21-35-5к

4000

750

370

5620

95

30120

0,00138

0,000174

0,001027

10

Примечание: для всех двигателей перегрузочная способность

l=Iдоп /Iн равна 2,4; LЯ =5.5 Uн /2pnн Iн –индуктивность якоря.

Расчетные формулы для определения параметров системы управления следующие:

СеФ = 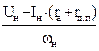, где: Rя = ra + rдп , wн = pnн /30;

Kд = ; Тя = ; Тм = , где: .

1. Принимая во внимание, что САУ электроприводом с применением ПИД- или ПИ- регулятора будет астатической, то требуемое значение коэффициента усиления датчика скорости Кдс можно найти по формуле:

Uз = 10 = Кдс wн Кдс = 10/ wн .

2. При настройке системы на модульный оптимум не скомпенсированной малой постоянной времени будет Tтп . При этом передаточную функцию регулятора скорости следует принять в виде: Wрс (р)= (Tя Tм р2 + Тм р +1)/ Ти р.

Тогда передаточная функция разомкнутой скорректированной

системы будет иметь вид:

,

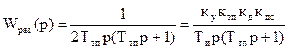Откуда определяется величина Ти регулятора скорости. Структурная схема ПИД-регулятора приведена ниже.

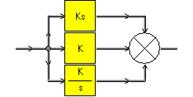
где: ks = (Tя Тм /Ти )s, K=Тм /Ти , К/s = 1/Ти s – параметры ПИД-регулятора.

3. Коэффициент компенсации b, обеспечивающий астатизм второго порядка по управлению, можно определить в соответствии с выражением: 1 – b ктп кд кдс =0.

В этом случае из числителя передаточной функции по ошибке от управляющего воздействия можно вынести оператор Р, что соответствует повышению порядка астатизма на 1.

4. Величину постоянной заводки задатчика интенсивности, позволяющего плавно разгонять нагруженный электропривод с максимально-допустимым динамическим моментом можно рассчитать из основного уравнения движения:

Мд - Мс = Jд dw/dt, где: Мд = lIн (См Ф); Мс = Iн (См Ф); (См Ф)=(Се Ф); dw=wн .

Тогда dt = tпуска .

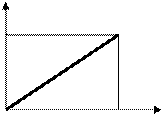Uз

10

tпуска t

5. Для определения скоростной ошибки по моменту нагрузки необходимо взять передаточную функцию по ошибке от возмущающего воздействия без учета компенсирующего устройства по управляющему воздействию.

6. Смоделировать САУ с применением пакета SyAn и провести экспериментальные исследования для подтверждения расчетов по пунктам 15.

Модель двигателя постоянного тока в зависимости от соотношения постоянных времени якорной цепи представляется или колебательным звеном, или апериодическим 2-го порядка, т.е.:

Wдпт (р)=w(р)/Uд (р)=Кд /(Tя Tм р2 + Тм р +1)=Кд /(Т1 р + 1)(Т2 р + 1) если 4Тя Тм ;

Wдпт (р)=w(р)/Uд (р)=Кд /(Tя Tм р2 + Тм р +1)=Кд /(Т2 р2 + 2xТр + 1) если 4Тя Тм ,

где: , 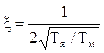- параметры колебательного звена.

Структурная схема ДПТ для исследования влияния нагрузки может быть представлена в виде (для случая 4Тя Тм ):

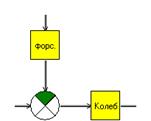где форс. - Rя (Tя р +1) /(СеФ).

В отчете по лабораторной работе должны быть представлены л.ч.х. и графики переходных процессов по управлению и возмущению в скорректированной комбинированной системе.

ЛАБОРАТОРНАЯ РАБОТА № 3

Исследование САУ с наблюдающим устройством идентификации

Цель работы: получение практических навыков настройки адаптивного регулятора.

Задание на лабораторную работу: для системы управления скорости двигателя постоянного тока (ДПТ) с независимым возбуждением применено адаптивное наблюдающее устройство идентификации рис. 3.

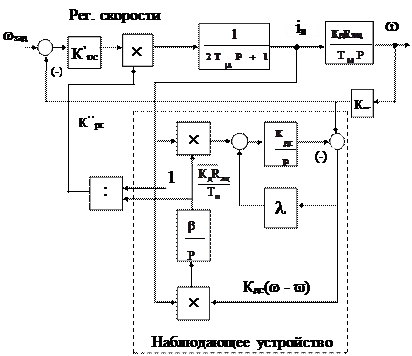Структурная схема

Рис.3.

Предполагается, что контур тока настроен на модульный оптимум с ПИ – регулятором, и передаточная функция замкнутого контура тока имеет вид

1/(2Тm р + 1).

Принять величину нескомпенсированной малой постоянной времени Тm =0.02 с. Для простоты считаем, что в замкнутой следящей системе обратной связью по ЭДС двигателя можно пренебречь и момент нагрузки отсутствует. Электропривод представляет из себя нестационарную систему, т.к. могут меняться или приведенный момент инерции Jд , или параметры якорной цепи - Kд , Rяц . В качестве управляющего воздействия на нестационарную часть объекта рассматривается ток двигателя Iя , а в качестве выходной координаты – скорость двигателя w. Предположим, линейная часть объекта неизвестна и имеет передаточную функцию

W(p) = w/Iя = b/p, где b =Rяц Кд /Тм .

Требуется:

1. Применяя П-регулятор скорости, рассчитать его передаточный коэффициент Крс при условии настройки на модульный оптимум. Разделить его на два сомножителя, представляющие постоянную и переменную величины.

2. Построить модель САУ скоростью электропривода без адаптивного наблюдающего устройства и получить основной переходный процесс по скорости, определить его параметры с рассчитанным в п.1 коэффициентом Крс .

3. Исследовать влияние на параметры основного переходного процесса изменений момента инерции в САУ.

4. Построить модель адаптивного наблюдающего устройства и опытным путем найти коэффициенты l и b из условия протекания в системе процесса оценки быстрее основного переходного процесса.

5. Исследовать влияние на параметры основного переходного процесса изменений момента инерции в САУ с адаптивным наблюдающим устройством.

Порядок выполнения работы

Исходные данные объекта управления ( электропривода) взять из лабораторной работы «Исследование САУ с комбинированным управлением».

1. Для приведенной на рис.1 структурной схемы при настройке контура тока на МО (модульный оптимум) требуемый коэффициент регулятора скорости рассчитывается по формуле (для получения МО в контуре скорости):

Разделить Крс на два сомножителя Крс =К’ рс К’’ рс , где К’ рс = 1/4Тm Кдс – постоянная величина,

а К’’ рс = Тм /Кд Rяц – переменная величина.

2. Подавая на вход САУ скоростью электропривода единичное ступенчатое воздействие, убедиться, что на выходе (скорость) будет переходный процесс с перерегулированием не более 4,3 % и временем » 20 Тm . Также вывести значение тока якоря двигателя.

3. Момент инерции Jд определяет значение постоянной времени Тм , поэтому, изменяя в объекте управления Тм в пределах (0.52.0) Тм , оценить (построить) зависимости перерегулирования (колебательности) и времени регулирования от момента инерции САУ.

4. При построении адаптивного наблюдающего устройства в общем случае объект управления характеризуется передаточной функцией любого порядка. Но степень числителя ее должен быть по крайней мере на единицу меньше степени знаменателя

Коэффициенты Аi и Вi могут быть неизвестны и подлежат восстановлению.

Разделив числитель и знаменатель передаточной функции объекта на полином (n-1) степени (р+l2 ) (р+l3 ) (р+ln ), где l2 , l3 ,ln – действительные и отрицательные корни, и разложив числитель и знаменатель на простые дроби, а также учтя первый корень l1 , получим

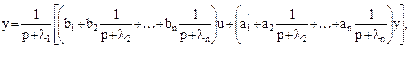
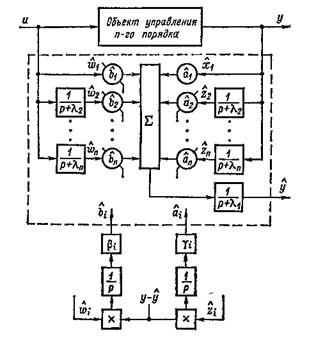
где а’ 1 =а1 +l1 , а1 =(l2 ++ln ) – А1 , b1 =B0 . Остальные коэффициенты bi и ai связаны сложными полиномами с параметрами Ai , Bi и lI и здесь не приводятся. На основании полученного уравнения можно построить структурную схему наблюдающего устройства (рис.4).

Структурная схема наблюдающего устройства

Рис.4

где: - оценочные значения параметров аi и bi ; - промежуточные переменные; gI , bI – коэффициенты усиления цепей адаптации, предназначенные для настройки параметров и . Они выбираются из условия обеспечения минимального времени адаптации при одновременном обеспечении устойчивой работы наблюдателя.

Для объекта первого порядка, исследуемого в данной лабораторной работе, алгоритм работы наблюдающего устройства может быть описан уравнениями

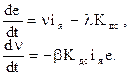
где: е=w - v и n=( Rяц Кд /Тм ) - (Rяц Кд /Тм ).

Асимптотическую устойчивость наблюдающего устройства можно проверить с помощью функции Ляпунова в виде положительно-определенной квадратичной формы:

Набрать модель наблюдателя (рис.5) и, изменяя значения параметров l(100010000) и b(5002000), добиться устойчивой его работы, при этом время адаптации должно быть намного меньше времени переходного процесса, полученного в п.2.

Модель наблюдающего устройства

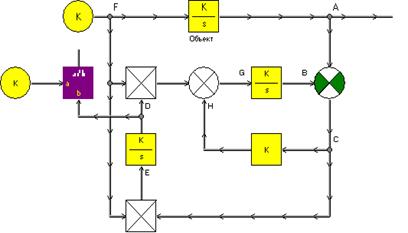
Рис.5

Удостовериться, что в точке D значение оцениваемого параметра равно заданному в объекте.

Собрать полную модель системы регулирования совместно с наблюдающим устройством и для различных Jд получить переходные процессы по скорости и току двигателя. Переходные процессы по скорости должны быть одинаковыми.

На рис.6 приведена полная схема электропривода с адаптивным наблюдающим устройством. Следует при моделировании задаться начальными условиями интегратора с параметром b. При этом принять начальные условия, близким или Кд Rяц /(Tм b).

Модель ЭП с наблюдателем

Объект

наблюдатель

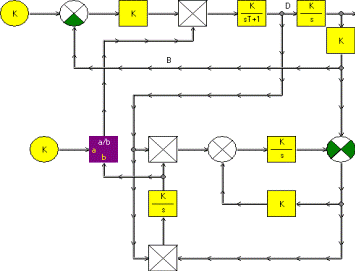
Рис.6

В отчете по лабораторной работе должны быть представлены структурные схемы, модели и переходные процессы исследуемой системы при различных значениях параметров объекта.

ЛАБОРАТОРНАЯ РАБОТА № 4

Исследование одномерной экстремальной САУ

Цель работы: получение практических навыков настройки экстремального регулятора.

Экстремальные системы целесообразно применять в следующих случаях:

1) если существует показатель качества, с изменением которого про­исходит достаточно ощутимое изменение технико-экономической эф­фективности;

2) когда выгоды от увеличения технико-экономической эффектив­ности существенно компенсируют затраты, обусловленные примене­нием принципа экстремального управления;

3) если существуют возможности определения экстремума функ­ционала качества и воздействия на регулирующие органы объекта с целью получения экстремального режима его работы.

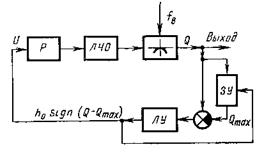
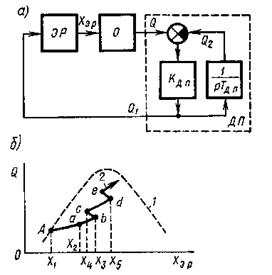
Экстремальное управление применяют также в сложных системах комплексной автоматизации. При этом ставится задача определения оптимальных настроек локальных регуляторов автоматических си­стем из условия экстремума некоторого показателя качества в стати­ческих или установившихся режимах при различных возмущениях, нарушающих экстремальный режим. На рис.7 представлена система с запоминанием экстремума.

Управляющее воздействие на линейную часть объекта (ЛЧО) системы формируется в результате вы­явления разности между текущим значением показателя качества и его экстремальным значением. В качестве регулятора (Р) чаще всего используется сервопривод. Для определения экстремального значения показателя качества используют запоминающее устройство (ЗУ), включаемое параллельно каналу, через который проходит сигнал текущего значения показателя качества.

Функциональная схема одномерной релейной

экстремальной САУ

Рис.7

ЗУ реагирует только на увеличение сигнала Q (при максимуме). До тех пор, пока максимум не достигнут, сигналы, поступающие на элемент сравнения, равны и их разность равна нулю. После достижения экстремального значения Qmax показатель качества при дальнейшем увеличении сигнала X на входе экстремального звена будет уменьшаться. В результате этого появится сигнал на входе логического устройства (ЛУ), формирующий сигнал управления U = h 0 sign (Q — Qma x) и воздей­ствующий на систему так, чтобы происходило уменьшение сигнала X и возрастание показателя качества Q . После срабатывания ЛУ сигнал поступает на стирание Qmax в ЗУ. Далее процесс поиска экстремума повторяется. Система с запоминанием экстремума является релейной, поэтому протекающие в ней процессы будут иметь колебательный харак­тер. Амплитуда колебаний показателя качества определяется величи­ной зоны нечувствитель­ности релейного элемента, формирующего сигнал уп­равления в функции раз­ности Q — Qmax .

Достоинством систем с запоминанием экстремума является сравнительно не­большая амплитуда коле­баний параметров в про­цессе поиска. К недостат­кам этих систем относится необходимость применения стабилизирующих устройств, входящих в ЛУ. Объясняется это тем, что при влиянии помех, например, смещающих экстремальную харак­теристику вверх, сигнал на входе ЛУ будет равен нулю, и изменения знака управляющего сигнала не произойдет. В результате этого прин­цип работы системы нарушается. Для обеспечения устойчивости ра­боты системы используют специальные способы стабилизации. С целью улучшения процессов в экстремальных системах данного типа на вход ЗУ можно подавать кроме сигнала Q его производные и предусматри­вать соответствующие устройства связи выхода ЛУ с ЗУ. Системы с за­поминанием экстремума наиболее целесообразны для малоинерционных объектов, имеющих высокочастотные помехи.

Задание на лабораторную работу:

1. Применяя пакет прикладных программ SyAn построить модель экстремальной системы, представленной на рис.7. ЛЧО принять в виде апериодического звена 1-го порядка с коэффициентом усиления 1и постоянной времени То . Экстремальная статическая характеристика имеет вид: Q* = - КX* 2 . Регулятор представляет собой идеальный интегратор 1/(Ти p). ЛУ взять в виде трехпозиционного реле с зоной нечувствительности (амплитуда 1, а скважность e изменяется от 0 до 1).

2. Исследовать влияние на показатели качества САУ величины Ти , То и e.

3. С целью улучшения качества работы экстремальной системы применить динамический преобразователь (ДП) в виде реального дифференцирующего звена.

4. Провести настройку и исследование качества с быстродействующим экстремальным регулятором.

Порядок выполнения работы

Параметры объекта и регулятора задаются преподавателем.

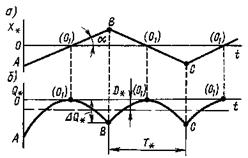
Основными показателями качества процессов поиска релейных одномерных экстремальных систем являются: время поиска экстремума, амплитуда и период колебаний, потери на поиск экстремума. Эти системы характеризуются наличием поисковых колебаний («рысканий») около экстремума. Из рис. 7,а устанавливаем, что при постоянной скорости изменения входной переменной в интервале 0.5Т* i t Т* i

X* =±K1 t, где K1 = tg a.

Диаграмма «рыскания»

Рис. 7

Период Т* i «рысканий» системы определяется моментом переключения реле рис. 2,б. Тогда отклонение экстремального параметра на одном участке периода:

Q* = - K K1 2 t2 .

Скорость изменения этого отклонения на участках между переключениями 0.5Т* i t Т* i определяется производной

dQ* /dt = - 2K K1 2 t.

Среднее за период поиска «рыскания» значение отклонения экстремального параметра называют потерей на поиск (см. рис.7,б):

D* =-K(K1 T*i )2 /12.

Амплитуда колебаний экстремального параметра получается подстановкой (см. рис.7,б) t = 0,5 T* i :

DQ* = - 0.25 K (K1 Т*i )2 ,

т.е. амплитуда «рысканий» в три раза больше потерь на «рыскание»:

DQ* = 3 D* .

Амплитуда колебаний и потери на поиск зависят от формы экстремальной характеристики и нелинейно зависят от периода колебаний.

Чтобы улучшить качество работы экстремальных систем, необхо­димо повысить их быстродействие (уменьшить время выхода на экстре­мум после смещения характеристики объекта), уменьшить амплитуду автоколебаний и снизить потери на поиск. Для этого применяют из­вестные методы коррекции автоматических систем. Специфика экстре­мальных систем, имеющих нелинейные звенья, обусловливает слож­ность задач синтеза корректирующих устройств.

В ряде случаев для улучшения качества работы экстремальных систем используют инженерные рекомендации [7]. Например, для уменьшения времени поиска в системах с запоминанием экстремума и с коммутатором (см. рис. 8) А. П. Юркевич предложил применять динамический преобразователь входного сигнала экстремального регулятора в виде реального дифференцирующего звена, который выполняет роль последовательного корректирующего устройства, включаемого между выходом одномерного объекта (О) и экстремальным регулятором (ЭР) — рис. 8, а.

Динамический преобразователь

Рис. 8

Структура динамического преобразователя (ДП) представлена в виде безынерционного звена, охваченного отрицатель­ной обратной связью, содержащей идеальный интегратор [9]:

Wдп (р) = Кдп /(1+ Кдп /р Tдп ),

где Кдп и Тдп - коэффициент передачи и постоянная времени ди­намического преобразователя.

Рассмотрим процесс поиска экстремума системы с запоминанием экстремума и динамическим преобразователем ( рис. 8,6). Пусть на­чальная точка работы экстремальной системы после смещения харак­теристики Q(Xэр ) соответствует точке А на кривой 1. В результате действия ЭР сигнал Xэр будет увеличиваться и при ве­личине Х2 значение Q1 = Q (точка а). Затем, после того как Q2 станет больше Q, сигнал Q1 начнет уменьшаться. Это вызовет сраба­тывание ЭР при значении сигна­ла Хэр = Х3 (точка b ), осу­ществляющего «ложный» реверс. Далее уменьшается сигнал Хэр до величины Х4 , когда снова произойдет реверс ЭР (точка с). При значении Х5 осуществляется последующий «ложный» ре­верс ЭР (точка d ) и т. д. Введе­ние ложных реверсов ускоряет движение к экстремуму (см. кри­вую 2 на рис. 8, б). Если ха­рактеристика Q (Хэр ) дрейфует, то в результате действия ДП и ЭР система следит за смеще­нием экстремума. Чем меньше инерционность объекта О, тем эффективнее действие ДП.

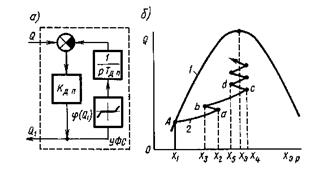
Для улучшения процессов поиска экстремума инерционных объектов высокого порядка, а также нейтральных и неустойчивых объектов В. В. Казакевичем предложен быстродействующий экстремальный регулятор — ЭРБ [7], в котором осуществляется поиск экстремума по максимуму производной (dQ/dt)max , реализуемый с помощью устройства формирования входного сигнала — УФС (рис. 9, а), представля­ющего собой автоматический компенсатор. Скорость компенсации при этом настраивается соответственно свойствам объекта.

В отличие от динамического преобразователя УФС имеет нелинейную обратную связь (реверсивный двигатель автоматического компенсатора). На линейных участках харак­теристики j (Q1 ) структурная схема УФС эквивалентна структурной схеме ДП. В пределах зоны нечувствительности характеристики j (Q1 ) сигнал производной dQ/dt = 0.

Устройство формирования сигнала

Рис.9

Это означает, что при медленном изменении сигнала Q (при медленном смещении Q (X) и при малом наклоне характеристики Q (X) вблизи экстремума) на вход экстремального регулятора будет поступать сигнал, пропорциональный параметру Q, без его производ­ной. Следовательно, ЭРБ обеспечивает слежение за экстремумом при медленном изменении Q и форсированно выводит объект в область экстремума при быстром смещении характеристики Q (X).

Рассмотрим процесс поиска экстремума системы с ЭРБ и комму­татором. Пусть начальная точка работы экстремальной системы после смещения характеристики Q (Хэр ) соответствует точке А на кривой 1 (рис. 9, б ). В результате действия коммутатора и УФС при значе­нии X 2 происходит ложный реверс (точка a ), а при значении Хз - последующий реверс от действия УФС (точка b ). При значении Хэр = = Хэ производная dQ/dt достигает максимума. После того как Q2 станет больше нуля, сигнал Q1 уменьшится и при Хэр = Х4 ЭРБ произведет ложный реверс (точка c ). Затем при Х5 произойдет реверс от действия УФС (точка d ) и т. д. Система форсированно выводит объект в область экстремума (кривая 2 на рис. 9, б ). Вблизи экстре­мума при малой величине dQ/dt система перейдет на поиск экстремума по параметру Q.

В процессе форсированного поиска система с ЭРБ не переходит на противоположную ветвь характеристики Q (Хэр ), поэтому время по­иска для инерционных объектов по сравнению с регуляторами без ЭРБ уменьшается на порядок без ухудшения качества установившихся режимов.

Рассмотренные основные методы улучшения качества работы эк­стремальных систем применяются при разработке как одномерных, так и многомерных систем.

На Рис.10 представлена одна из возможных моделей экстремальной САУ без УФС и ДП.

Модель экстремальной САУ

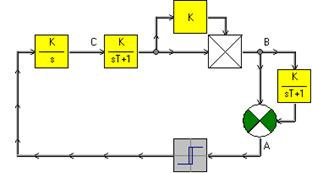
Рис.10

В отчете по лабораторной работе привести как временные так и фазовые характеристики поиска экстремума. Кроме того в выводах по работе должен содержаться сравнительный анализ влияния на показатели работы экстремальной системы ее параметров и методов поиска.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Советов, Б.Я. Моделирование систем: Учеб. для вузов – 3-е изд.,перераб. и доп./Б.Я.Советов, С.А.Яковлев. – М.: Высш. шк., 2001. –343 с.: ил.

2. Веников, В.А. Теория подобия и моделирование/ В.А. Веников, Г.В.Веников . – М.: Высш. шк., 1984. –243 с.: ил.

3. Коршунов, Ю.М. Математические основы кибернетики: Учеб. пособие для вузов/Ю.М.Коршунов. - М.: Энергоатомиздат, 1987.- 496 с.: ил.

4. Бусленко, Н.П. Моделирование сложных систем/Н.П.Бусленко.-М.: Наука, 1978.-399 с.: ил.

5. Справочник проектировщика АСУ ТП/ Г.Л.Смилянский, Л.З.Амлинский, В.Я.Баранов и др.; Под ред. Г.Л.Смилянского.-М.:Машиностроение, 1983.-527 с.: ил.

6. Шеридан, Т.Б. Системы человек – машина. Модели информации, управления и принятия решений человеком – оператором: Пер. с англ./Т.Б. Шеридан, У.Р.Феррелл. - М.: Машиностроение, 1980. - 400 с.: ил.

7. Казакевич, В.В. Системы автоматической оптимизации /В.В.

Казакевич, А.Б. Родов.- М.: Энергия, 1977.- 384 с.: ил.

8. Иващенко, Н.Н. Автоматическое регулирование/Н.Н.Иващенко. - М.: Машиностроение, 1978. - 609 с.: ил.

9. Куропаткин, П.В. Оптимальные и адаптивные системы/П.В.Куропаткин. –М.: Высш. шк., 1980. –288 с.

10.Топчеев, Ю.И. Атлас для проектирования систем автоматического регулирования/Ю.И.Топчеев. - М.: Машиностроение, 1989. - 752 с.: ил.

11.Сю, Д. Современная теория автоматического управления и ее применение: Пер. с англ./Д.Сю, А.Мейер. -М.: Машиностроение, 1972. –552 с.: ил.

12. Официальный сайт МИРЕА. Режим доступа:

http://www.cpd.mirea.ru/

СОДЕРЖАНИЕ

Стр

1. Исследование системы с нечетким управлением….…...3

2. Исследование САУ с комбинированным

управлением………………………………………………15

3. Исследование САУ с наблюдающим устройством

идентификации ……………..…………………………..21

4. Исследование одномерной экстремальной САУ……….27

Скачать архив с текстом документа