Методические указания по практическим работам По дисциплине

СОДЕРЖАНИЕ: «Методы исследования и моделирования национальной экономики» включают тематику вопросов, выносимых для самостоятельной подготовки, задачи, которые решаются студентами под контролем преподавателя или самостоятельно во время аудиторных занятий

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

Тихоокеанский государственный университет

Институт экономики и управления

Кафедра Экономическая кибернетика

Методические указания по практическим работам

По дисциплине

Методы исследования и моделирования

национальной экономики

Для специальности

080103.65 «Национальная экономика»

Методические указания разработаны в соответствии с составом УМКД

Методические указания разработала Порошина Л.А. _____________

Методические указания утверждены на заседании кафедры,

протокол № ______ от «___» _______________ 200__ г.

Зав. кафедрой _________ «___» ______________ 200__ г. Пазюк К.Т.

Методические указания по практическим занятиям по дисциплине «Методы исследования и моделирования национальной экономики» включают тематику вопросов, выносимых для самостоятельной подготовки, задачи, которые решаются студентами под контролем преподавателя или самостоятельно во время аудиторных занятий.

Методические указания рассмотрены и утверждены на заседании УМКС и рекомендованы к изданию

протокол № ______ от «___» _______________ 200__ г.

Председатель УМКС _______ «___» __________ 200__ г.

Директор института _________ «___» ____________ 200__ г. Зубарев А.Е.

1. ЦЕЛИ И ЗАДАЧА ДИСЦИПЛИНЫ

ГОСом предусмотрено, что студент специальности НЭ должен:

· иметь системное представление о структурах и тенденциях развития российской и мировой экономик;

· понимать многообразие экономических процессов в современном мире, их связь с другими процессами, происходящими в обществе;

Целью преподавания дисциплины является формирование знаний, умений и практических навыков моделирования управленческих решений.

Предметом изучения названной дисциплины являются количественные характеристики экономических процессов на основе экономико-математических методов и моделей. В курсе рассматриваются конкретные задачи и их экономико-математические модели. Это модели балансовые, имитационные, эконометрические.

Немалое место отводится моделям оптимального отрасле­вого и регионального регулирования – экономико-математическим моделям проекта развития отдельных отраслей народного хозяйства.

Освещаются модели народнохозяйственного регулирования (в частности, межотраслевого баланса, базовые, статистические и динамические модели, модели ценообразования на основе межотраслевого баланса, моделирование спроса и предложения). Представляется модель взаимосвя­зи конечного использования и валового продукта. Излагаются вопросы сингулярных моделей макроэкономического прогнозирования.

Основным понятием курса является понятие математи­ческой модели. В общем случае слово модель – это отражение реального объекта. Такое отражение объекта может быть пред­ставлено схемой, эскизом, фотографией, моделью описательно­го характера в виде графиков и таблиц и т. д. Математическая модель – это система математических уравнений, нера­венств, формул и различных математических выражении, опи­сывающих реальный объект, составляющие его характеристи­ки и взаимосвязи между ними. Процесс построения математи­ческой модели называют математическим моделированием. Естественно, моделирование и построение математической моде­ли экономического объекта позволяют свести экономический анализ производственных процессов к математическому ана­лизу и принятию эффективных решений.

2. КРАТКИЕ ХАРАКТЕРИСТИКИ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

Тема 1. Моделирование микроэкономических процессов и систем

Задание. Разработка математической модели производственного процесса.

Исполнение . Решение производственной задачи с применением обоснованного математического инструментария. Интерпретация результатов решения. Обоснование устойчивости решения.

Оценка . Формируют необходимые представления о применимости того или иного математического инструментария к заданному классу производственных задач.

Время выполнения заданий : 11 часов.

Примеры решаемых задач.

Пример 1.

Объем продажи некоторого магазина составляет в год 500 упаковок супа в пакетах. Величина спроса равномерно распределяется в течение года. Цена покупки одного пакета равна 2 руб. За доставку заказа владелец магазина должен заплатить 10 руб. Время доставки заказа от поставщика составляет 12 рабочих дней (при 6-дневной рабочей неделе). По оценкам специалистов, издержки хранения составляют 20% среднегодовой стоимости запасов. Необходимо определить: 1) сколько пакетов должен заказывать владелец магазина для одной поставки; 2) частоту заказов; 3) точку заказа. Известно, что магазин работает 300 дней в году.

Решение. Плановым периодом является год, пакетов в год, рублей, затраты на хранение одной единицы продукции в год составляют 20% от стоимости запаса в одну упаковку, т.е. рубля. Тогда

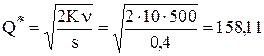пакетов.

Поскольку число пакетов должно быть целым, то будем заказывать по 158 пакетов. При таком заказе годовые затраты равны

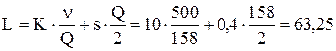рублей в год.

Подачу каждого нового заказа владелец магазина должен осуществлять через года. Поскольку известно, что в данном случае год равен 300 рабочих дней, то рабочих дней. Заказ следует подавать при уровне запаса равном пакетам,

т.е. эти 20 пакетов будут проданы в течение 12 дней, пока будет доставляться заказ.

Пример 2.

Решение. Когда затраты на заказ равны 10 рублей, затраты на хранение продукции 1 рубль в сутки, интенсивность потребления товара 5 шт. в день, цена товара 2 рубля за штуку, а при объеме закупки 15 шт. и более - 1 рубль. Определить оптимальный размер заказа.

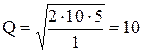руб., шт. в день, за шт. в сутки, руб. за шт., шт., руб. за шт.

шт.,

т.е. условие шага 2 алгоритма не выполняется . Найдем размер заказа , уравнивающий общие затраты при различном уровне цен

,

,

,

,

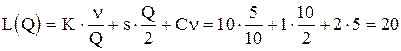
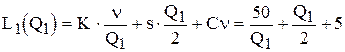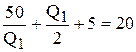шт. или шт.

Согласно шагу 2 выбираем большее значение шт., которое находится в области 2. Таким образом выполняется условие шага 3 алгоритма, т.е. (), поэтому шт. Общие затраты в единицу времени составляют

,

тогда как если бы заказывали по 10 шт. товара, то общие затраты составили бы 20 рублей, т.е. при заказе в 15 шт. экономия средств составляет 4,17 рублей в сутки.

Пример 3.

На некотором станке производятся детали в количестве 2000 штук в месяц. Эти детали используются для производства продукции на другом станке с интенсивностью 500 шт. в месяц. По оценкам специалистов компании, издержки хранения составляют 20% средней стоимости запасов в год. Стоимость производства одной детали равна 2,50 руб., а стоимость на подготовку производства составляет 1000 рублей. Каким должен быть размер партии деталей, производимой на первом станке, с какой частотой следует запускать производство этих партий ?

Решение. руб., шт. в месяц или 24000 шт. в год, шт. в месяц или 6000 шт. в год, руб. в год за деталь.

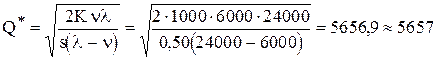шт.

Частота запуска деталей в производство равна

года или 11,28 месяцев.

Общие затраты на УЗ составляют

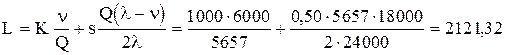руб. в год.

Тема 2. Моделирование макроэкономических процессов и систем

Задание. Разработка постановки задачи размещения производственных сил в регионе, обоснование исходных данных для постановки задачи.

Исполнение . Обоснование и выбор аппарата моделирования, инструментария решения задачи. Решение на ЭВМ. Интерпретация решения: объемов производства продукции и транспортировки потребителям.

Оценка . Формирует типологию межотраслевых отношений в регионе.

Время выполнения задания : 11 часов.

Решим задачу потребительского выбора.

Пример 4.

Оптимальный набор потребителя составляет 6 ед. продукта х₁ и 8 ед. продукта х2. Определите цены потребляемых благ, если известно, что доход потребителя равен 240 руб. Функция полезности потребителя имеет вид: u(x₁ ,x₂ )=xx.

Решение. Следуя принципу решения, получаем систему уравнений:

=, =, =,

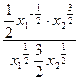p₁ x₁ +p₂ x₂ =240. p₁ x₁ +p₂ x₂ =240 . p₁ x₁ +p₂ x₂ =240 .

Подставив, вместо х₁ – 6 ед ., вместо х₂ – 8 ед ., получим: p ₁ =10 руб., p ₂ =22.5 руб.

Пример 5.

Изменение спроса на товар и предложение товара в зависимости от установленной цены представлено в таблице.

№	Цена (у.д.е. за шт), Р	Спрос (тыс. шт. в месяц), Qd	Предложение (тыс. шт. в месяц), Qs
1	22	12	75	12,0 88 89	71,666 67
2	20	25	65	23,288 89	65,166 67
3	18	30	55	34,488 89	58,666 67
4	16	45	50	45,688 89	52,166 67
5	14	60	46	56,888 89	45,666 67
6	12	70	40	68,088 89	39,166 67
7	10	80	35	79,288 89	32,666 67
8	8	90	25	90,488 89	26,166 67
9	6	100	20	101,688 9	19,666 67

На основании приведенных данных необходимо:

1. Построить кривые спроса и предложения.

2. Определить функции спроса и предложения, построить их графики.

3. Определить равновесную цену и равновесный объем продаж.

4. Определить ситуацию, которая установится на рынке, если цена товара составит 12 у.д.е. и 17 у.д.е.

5. Определить, возможно ли достижение точки равновесия. Построить паутинообразную модель, в качестве исходной цены взять значение 8 у.д.е.

6. Определить эластичность спроса и предложения относительно цены (в общем виде и по отдельным точкам значений цен).

7. Пусть на рынке имеется второй товар. Отмечено, что снижение цены на второй товар с 11 до 5 у.д.е. привело к падению спроса на первый товар с 95 до 60 тыс.шт. в месяц. Определить перекрестную эластичность спроса.

Решение .

1. Кривые спроса и предложения, а также графики функций спроса и предложения приведены на рис. 1.

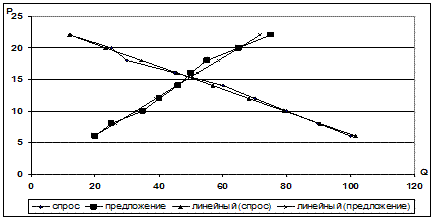
Рис. 1 – Кривые спроса и предложения

2. Определим функции спроса и предложения. Предположим, что объемы спроса и предложения зависят от цены линейным образом.

В этом случае расчетные значения спроса и предложения можно представить следующим образом:

(1)

(2)

где – коэффициенты уравнений регрессии.

Эти параметры найдем с помощью приложения Microsoft Excel. Запустите данное приложение. На экране откроется основное окно для ввода исходных данных. Внесите по столбцам значения Р, Qd и Qs, как это показано на рис. 2.

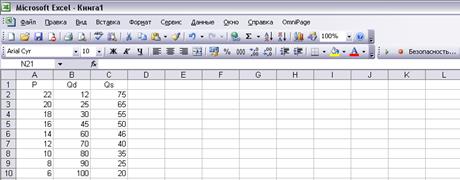
Рис. 2 – Исходные данные

Для получения уравнения регрессии спроса от цены и предложения от цены, выберем пункт меню «Сервис», на экране появится подменю, выберите в нем категорию «Анализ данных». Откроется список функций, среди которых следует выбрать функцию «Регрессия» и нажать кнопку «ОК» (рис. 3.)

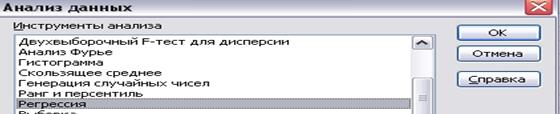
Рис. 3 – Анализ данных

Откроется диалоговое окно. Оно имеет два поля ввода для указания данных (рис. 4).

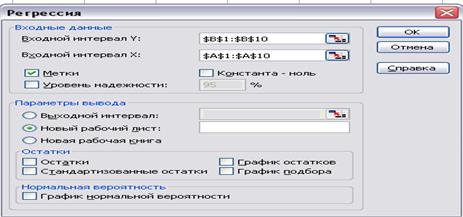
Рис. 4

Щелчком по флажку поля «Входной интервал Y» окно ввода сверните, затем выделите курсором массив столбца Qd, снова щелкните по флажку и окно ввода разверните до первоначального вида. В поле «Входной интервал Y» появится адрес массива столбца Qd. После этого введите адрес массива столбца Р в поле «Входной интервал X», для чего щелкните по флажку «Входной интервал X» и аналогично предыдущему выделите массив столбца Р. Повторным щелчком по этому флажку окно ввода разверните до первоначального вида. Поставьте галочку в окне метки. Затем щелчком по кнопке «ОК» завершите операцию задания интервалов. Откроется окно отчета (рис. 5).

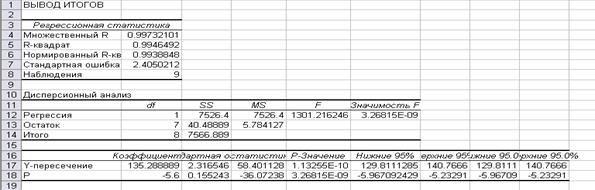
Рис. 5

Из отчета в таблице коэффициентов выпишем значения коэффициентов:

Таким образом, функция спроса имеет следующий вид:

(3)

Оценим точность полученного уравнения регрессии. Для этого воспользуемся процедурой дисперсионного анализа. Приведем следующие формулы для вычисления остаточной дисперсии (² _ост ), коэффициента множественной детерминации (R² ) и значения критерия Фишера (F).

– сумма квадратов остатков;

– сумма квадратов отклонений за счет регрессионной зависимости;

сумма квадратов отклонений Qd.

Коэффициент множественной детерминации (R² ) показывает долю вариации результативного показателя, обусловленную вариацией включенных в уравнение регрессии независимых переменных.

. (4)

Остаточная дисперсия применяется в качестве меры рассеяния наблюдений вокруг линии регрессии:

;

.

Для определения значимости уравнения регрессии, т.е. верно ли уравнение регрессии описывает фактическую зависимость, используется F-критерий Фишера:

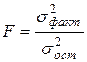, (5)

где N – число наблюдений, в нашем случае N=9; m – число независимых переменных, включенных в уравнение регрессии; – среднее значение объема спроса.

В нашем примере R² =0,994 6, это означает, что изменение спроса на 99,5% объясняется изменением цены на товар, а оставшиеся 0,5% – изменения, обусловленные неучтенными факторами.

Значение R² изменяется в диапазоне [0;1]. Чем ближе R² к 1, тем лучше подобрана регрессия.

В столбце значимость F указана вероятность того, что гипотеза о значимости уравнения регрессии неверна (PV). В нашем случае PV= 3,26·10^-9 (3,26Е-09), т.е можно считать, что гипотеза о значимости уравнения верна. Значение F=1 301,216 можно сравнить с табличным и на основании этого сравнения сделать вывод о значимости уравнения регрессии.

Аналогичные шаги проделайте для определения функции предложения. Только теперь в поле «Входной интервал Y» необходимо внести адрес массива столбца Qs, выделив при этом курсором массив этого столбца. Данные поля «Входной интервал X» останутся без изменений (рис. 6).

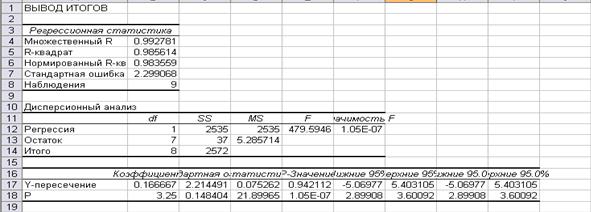
Рис. 6

Из отчета выпишем: b₀ =0,166, b₁ =3,25. Искомая функция предложения имеет вид:

. (6)

Оценки этого уравнения следующие: R² =0,985, PV = 1,05·10^-7 , F=479,59. Следовательно, данное уравнение также значимо и хорошо описывает зависимость между величинами Q_s и P .

3. Равновесную цену Ре и равновесный объем продаж Qe определим, зная, что в точке равновесия совпадают цены спроса и предложения, а также их объемы, т.е.

Pe=Pd=Ps и Qe=Qd=Qs.

В нашем случае при из (3) и (6) имеем 135,288 9–5,6Р=0,166+3,25Р. Отсюда равновесная цена Ре=15,268. Равновесный объем спроса и предложения составит (по уравнению (3)):

Qe=135,288 9–5,6·15,268=49,78

Проверим по уравнению (1.6): Qe=0,166+3,25·15,268=49,78.

Таким образом, при установлении цены на уровне 15,268 у.д.е. объем спроса и предложения совпадут и составят 49,78 тыс. шт. товара в месяц.

4. При установлении цены на уроне 12 у.д.е. спрос составит:

Qd=135,228 9–5,6·12=68,028 тыс. шт. товара в месяц

Предложение же при такой цене будет следующим:

Qs=0,166+3,25·12=39,166 тыс. шт. товара в месяц.

Таким образом, возникает дефицит товара в 28,862 тыс. шт.

Установление цены выше равновесной, а именно на уровне 17 у.д.е., приведет к превышению объема предложения над спросом на 15,388 тыс. шт. ()

5. Наклон кривой спроса и предложения определяет возможность достижения точки равновесия. Так, «паутина» сходится, если , расходится, если и зацикливается, если .

В нашем случае , следовательно, возможно достижение точки равновесия.

Построим паутинообразную модель исходя из заданной цены. По условию цена предшествующего периода была установлена на уровне 8 у.д.е., что определило предложение данного периода равным 26,166 тыс. шт. ). При таком предложении цена спроса устанавливается на уровне 19,48 у.д.е. (из (3) ).

В свою очередь, цена Р=19,48 определит предложение последующего периода на уровне 63,476 тыс. шт. (из (1.6) , но потребитель такое количество товара согласен приобрести лишь при установлении цены

Ориентируясь на цену 12,823 у.д.е.,

производитель в дальнейшем выпустит на рынок 41,84 тыс. шт. товара , которые покупатель согласен приобрести по цене у.д.е.

В конечном счете будет достигнута точка равновесия, Ре=15,268 7 у.д.е., полученная в п.3 задачи.

Траектория изменения цен и количества предлагаемого и требуемого товара представлена на рис. 7.

6. Эластичность спроса относительно цены находится по формуле

(7)

В нашем случае Следовательно, в общем виде

Эластичность предложения по цене определяется по формуле

. (8)

Учитывая, что имеем эластичность предложения по цене, равную .

Значения эластичностей спроса и предложения по цене для разных уровней цен представлены в таблице:

P	Qd	Qs
22	12	75	1,833	-10,264 8	0,293	0,952
20	25	65	0,8	-4,48	0,307	0,997
18	30	55	0,6	-3,36	0,327	1,062
16	45	50	0,355	-1,988	0,32	1,04
14	60	46	0,233	-1,304 8	0,304	0,988
12	70	40	0,171	-0,957 6	0,3	0,975
10	80	35	0,125	-0,7	0,285	0,926
8	90	25	0,088	-0,492 8	0,32	1,04
6	100	20	0,06	-0,336	0,3	0,975

Из таблицы видно, что спрос остается эластичным, т.е. растет быстрее, чем падает цена, до тех пор, пока цена остается в пределах от 22 до 14 у.д.е. Дальнейшее снижение цен происходит при более медленном нарастании спроса, т.е. спрос становится неэластичным.

Эластичность предложения по цене меняется слабо, при цене 18,16 и 8 у.д.е. предложение больше 1, в остальном диапазоне цен предложение растет медленнее, чем цены.

7. Перекрестная эластичность спроса рассчитывается по формуле

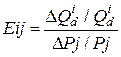, (9)

где i, j – индексы товаров; – изменение объема спроса на i-й товар; – изменение цены j-го товара где t и (t+1) – периоды времени).

Если Eij0, то товары взаимозаменяемы.

Если Eij0, то товары взаимодополняемы.

Если Eij=0, то товары независимы.

Находим , т.е. товары взаимозаменяемы, и снижение цены второго (j-го) товара на 1% влечет за собой падение спроса на первый (i-й) товар на 0,675%.

Пример 6.

Дан следующий отчетный межотраслевой баланс (МОБ) (пример условный):

Отрасли	1	2	3	4	5	6		Кон.прод.
1	17,54	128,29	0,55	0,82	0,00	14,61		0,89
2	18,81	180,24	59,90	107,77	14,75	82,23		316,25
3	11,11	76,43	626,56	239,67	61,72	61,06		306,34
4	5,95	29,71	91,16	70,61	85,06	78,49		527,47
5	6,12	34,31	39,15	41,62	48,38	101,34		159,19
6	10,83	97,17	162,28	89,19	61,55	279,84		1172,4

L 76 36 54 69 40 58

Ф 33 97 87 125 83 75

В шахматке указаны межотраслевые потоки промежуточной продукции, в последних двух строках (за пределами таблицы) – объемы затрат труда и фондов, а в последнем столбце – конечная продукция. Номенклатура отраслей следующая:

1. Сельское, лесное и рыбное хозяйство.

2. Тяжелая промышленность.

3. Легкая промышленность.

4. Строительство и энергетика.

5. Транспорт и связь

6. Услуги.

Необходимо:

1. Построить таблицу отчетного МОБ, проверить основное балансовое соотношение.

2. Составить плановый МОБ при условии увеличения спроса на конечный продукт по отраслям соответственно на 5, 4, 6, 7, 3 и 8 процентов.

3. Рассчитать коэффициенты прямых и полных затрат труда и фондов и проверить в плановом МОБе балансовые равенства.

4. Определить, насколько процентов необходимо увеличить производи-тельность труда по отраслям для выпуска планового валового продукта с той же численностью, что и в отчетном периоде.

5. Проследить эффект матричного мультипликатора при дополнительном увеличении конечного продукта по легкой промышленности на 5 %.

6. Рассчитать равновесные цены при увеличении зарплаты по всем отраслям на 10 % (считать доли зарплаты в добавленной стоимости по отраслям следующими: 0,33, 0,5, 0,52, 0,35, 0,43, 0,6). Проследить эффект ценового мультипликатора при дополнительном увеличении зарплаты в сельском хозяйстве на 5 %.

Решение.

Предполагается, что работа будет выполняться с помощью программы обработки электронных таблиц Microsoft Excel.

1. Заполним таблицу отчетного баланса (табл. 1).

Таблица отчетного МОБ

Таблица 1

Отрасли	1	2	3	4	5	6	Итого	Кон.продукт	Вал.про дукт
1	17,54	128,29	0,55	0,82	0,00	14,61	161,81	0,89	162,70
2	18,81	180,24	59,90	107,77	14,75	82,23	463,70	316,25	779,95
3	11,11	76,43	626,56	239,67	61,72	61,06	1076,55	306,34	1382,89
4	5,95	29,71	91,16	70,61	85,06	78,49	360,98	527,47	888,45
5	6,12	34,31	39,15	41,62	48,38	101,34	270,92	159,19	430,11
6	10,83	97,17	162,28	89,19	61,55	279,84	700,86	1172,40	1873,26
Итого	70,36	546,15	979,60	549,68	271,46	617,57	3034,82	2482,54	5517,36
Доб. ст.	92,34	233,80	403,29	338,77	158,65	1255,69	2482,54
Вал. пр.	162,70	779,95	1382,89	888,45	430,11	1873,26	5517,36

При составлении этой таблицы в Excel автоматически проверяется основное балансовое соотношение, суть которого состоит в равенстве суммарного конечного продукта (последняя ячейка столбца «Кон.продукт ») и суммарной добавленной стоимости (последняя ячейка строки «Доб. ст. ») в таблице 1 (2482,54=2482,54).

2. Для составления таблицы планового баланса необходимо рассчитать плановый валовой выпуск и плановые межотраслевые потоки.

Рассчитаем сначала коэффициенты прямых материальных затрат, используя информацию отчетного баланса:

0,108	0,164	0,000	0,001	0,000	0,008
0,116	0,231	0,043	0,121	0,034	0,044
0,068	0,098	0,453	0,270	0,143	0,033
0,037	0,038	0,066	0,079	0,198	0,042
0,038	0,044	0,028	0,047	0,112	0,054
0,067	0,125	0,117	0,100	0,143	0,149

После этого рассчитаем матрицу полных материальных затрат В, для чего сначала вычислим матрицу (Е-А), а затем найдем обратную к ней. Получаем матрицу В:

1,163	0,263	0,036	0,051	0,032	0,030
0,221	1,408	0,173	0,256	0,156	0,104
0,268	0,404	2,006	0,686	0,520	0,167
0,101	0,138	0,191	1,187	0,316	0,094
0,086	0,121	0,105	0,117	1,189	0,092
0,187	0,319	0,345	0,296	0,334	1,243

Для расчета планового валового выпуска необходимо вычислить плановый конечный продукт, увеличив отчетный по каждой отрасли на 5, 4, 6, 7, 3 и 8 (%). Получим:

0,93

328,90

324,72

564,39

163,97

1266,19

Определим плановый валовой выпуск:

171,61

820,88

1468,36

947,84

452,26

2012,74

Этот результат можно разместить сразу в столбце «Вал.продукт » таблицы планового баланса.

После соответствующих вычислений получим табл. 2, в которой размещен плановый МОБ.

Таблица планового МОБ

Таблица 2

	1	2	3	4	5	6	Итого	Кон.пр.	Х
1	18,50	135,02	0,58	0,87	0,00	15,70	170,68	0,93	171,61
2	19,84	189,70	63,60	114,97	15,51	88,35	491,98	328,90	820,88
3	11,72	80,44	665,28	255,69	64,90	65,61	1143,64	324,72	1468,36
4	6,28	31,27	96,79	75,33	89,44	84,33	383,44	564,39	947,84
5	6,46	36,11	41,57	44,40	50,87	108,89	288,29	163,97	452,26
6	11,42	102,27	172,31	95,15	64,72	300,68	746,55	1266,19	2012,74
Итого	74,21	574,81	1040,14	586,42	285,44	663,55		2649,11
Доб.ст	97,40	246,07	428,22	361,41	166,82	1349,19	2649,11
Х	171,61	820,88	1468,36	947,84	452,26	2012,74

Тем самым будет выполнен п.2 задания практической работы.

3. Для выполнения п.3 работы рассчитаем коэффициенты прямой трудоемкости и фондоемкости. Расчет будем проводить соответственно по формулам: t_j = L_j /X_j , f_j = Ф_j /X_j , копируя их в соответствующие клетки. Получим:

tj	0,467	0,046	0,039	0,078	0,093	0,031
fj	0,203	0,124	0,063	0,141	0,193	0,041

Рассчитаем коэффициенты полных затрат труда и фондов:

t 0,586	0,235	0,138	0,175	0,188	0,080
f 0,319	0,309	0,216	0,287	0,346	0,111

Подсчитаем плановую потребность в труде и фондах. Получим:

L	80,16	37,89	57,34	73,61	42,06	62,32		353,38
Ф	34,81	102,09	92,38	133,35	87,27	81,66		531,56

Первые 6 цифр – это потребность по отраслям, последние – по всей экономике.

4. Для выполнения четвертого пункта рассчитаем производительность труда по валовому продукту в отчетном периоде и в плановом, но численность возьмем в обоих случаях из отчетного баланса, а затем сравним эти результаты.

В отчетном периоде производительность труда по валовому продукту определяется делением величин валового продукта по отраслям на соответствующую численность. Получим:

2,141

21,665

25,609

12,876

10,753

32,298

Разделив валовой продукт планового периода на ту же численность, получим:

2,258

22,802

27,192

13,737

11,307

34,702

Как видим, производительность труда должна увеличиться. Определим это увеличение в процентах. Разделив одно на другое, получим:

1,055

1,052

1,062

1,067

1,051

1,074

Итак, наибольшее увеличение производительности труда (на 7,4 %) потребуется для 6-й отрасли – «услуги».

5. Эффект мультипликатора Леонтьева проследим, используя соотношение DX = B DY. DY рассчитаем из условия дополнительного увеличения спроса на конечный продукт по 3-й отрасли (легкой промышленности) на 5 %. Итак, спрос на конечную продукцию по всем отраслям, кроме 3-й, останется прежним, т. е. прирост спроса по этим отраслям будет равен нулю, а по 3-й отрасли такой прирост будет равен (324.72 * 0,05 = 16,236). Имеем,

DY = (0 0 16,236 0 0 0)^Т ,

тогда

DX = (0,48 2,29 26,65 2,52 1,39 4,57)^Т

(DX определено как произведение матриц B и DY). Как видим, по всем отраслям произошло изменение спроса на валовую продукцию. В процентном соотношении это составляет: (0,28 0,28 1,8 0,27 0,31 0,23).

6. Равновесные цены определим из соотношения P = B^T V, а доли добавленной стоимости рассчитаем по формуле v_j =z_j /x_j , изменив их затем из условия 10 %-го увеличения зарплаты. Разделив добавленную стоимость по отраслям на валовый выпуск, получим:

0,57

0,30

0,29

0,38

0,37

0,67

Выделим из добавленной стоимости зарплату, воспользовавшись информацией из задания п. 6 о долях зарплаты в добавленной стоимости. Получим:

0,19

0,15

0,15

0,13

0,16

0,40

Для расчета равновесных цен добавим 10 % от полученных величин к ранее рассчитанным и получим требуемую величину доли добавленной стоимости. Итак, v равно:

0,586

0,315

0,307

0,395

0,385

0,711

Для расчета по формуле P = необходимо протранспонировать матрицу коэффициентов полных затрат В. Получим равновесные цены:

1,0394

1,0487

1,0518

1,0448

1,0474

1,0574

Не забудьте, что в соответствии с правилами умножения матриц вектор V перед умножением должен быть представлен в виде столбца. Как видим, результаты расчетов показали, что при 10 %-м росте зарплаты одновременно по всем отраслям цены на продукцию отраслей увеличились в пределах от 3,94 % до 5,74 %. Рассчитаем теперь эффект ценового мультипликатора при дополнительном увеличении зарплаты по отрасли «сельское хозяйство» на 5 %. Расчеты будем вести по формуле DP = B^T DV, где DV определим из условия задачи.

DV = (0,0095 0 0 0 0 0)^Т ,

тогда

DP = (0,01105 0,0025 0,00034 0,0005 0,00031 0,00029).

Как и ожидалось, наибольший прирост в цене продукции пришелся на саму отрасль «сельское хозяйство» - увеличение на 1,1 %, а по остальным отраслям этот прирост составил доли процента. Например, по отрасли «тяжелая промышленность» на 0,25 %. Эффект же ценового мультипликатора проявился в том, что при изменении цены только в одной отрасли произошло изменение цен во всех отраслях и это изменение можно отследить с помощью ценового мультипликатора B^T

Тема 3. Производственные функции

Задание. Проведение анализа производственных функции и функций затрат.

Исполнение : решение задачи. Использование математического инструментария подготовки исходных данных и метода решения. Интерпретация результатов решения.

Оценка . Формирует необходимые представления об используемом математическом аппарате.

Время выполнения заданий : 12 часов.

Задание: Построение производственной функции и оценка ее адекватности.

Цель работы: Построение на ПК производственной функции по экспериментальным данным о затратах–выпусках.

Порядок выполнения работы.

1. Привести производственную функцию Кобба–Дугласа к линейному виду.

2. Воспользоваться таблицей согласно полученному варианту, в которой приведены динамические ряды по выпуску продукции и затрат ресурсов для оценки коэффициентов линейной регрессии.

3. Проверить критерий значимости коэффициентов регрессии и оп­ределить доверительные границы.

4. Определить коэффициент множественной детерминации.

5. Осуществить обратное преобразование путем потенцирования.

3. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ

Основная литература :

1. Абчук В.А. Экономико-математические методы. Санкт-Петербург: «СОЮЗ». 1999.

2. Акулич И.Л. Математическое программирование в примерах и задачах. Учебное пособие. М.: Высшая школа, 1986.

3. Багриновский Кирилл Андреевич. Имитационные модели в народохозяйственном планировании / Багриновский Кирилл Андреевич, H. Е. Егорова, В. В. Радченко. - М.: Экономика, 1980. - 199с.

4. Базилевич Леонид Анатольевич. Моделирование организационных структур / Базилевич Леонид Анатольевич; Под ред. В.Р. Окорокова. - Л.: Изд-во ЛГУ, 1978. - 159с.

5. Вильямс Н.Н. Параметрическое программирование в экономике. М.: Статистика, 1976.

6. Данциг Дж. Линейное программирование, его обобщения и приложения. М.: Прогресс, 1966.

7. Замков О.О. Математические методы в экономике: Учеб. / О. О. Замков, А. В. Толстопятенко, Ю. H. Черемных. - М.: Изд-во МГУ:ДИС, 1999. - 368с.

8. Зиядуллаев Hаби Саидкаримович. Моделирование региональных экономических систем / Зиядуллаев Hаби Саидкаримович. - М.: Hаука, 1983. - 240с.

9. Иванилов Ю.П. Математические модели в экономике: Учеб. пособие для вузов / Ю. П. Иванилов, А. В. Лотов; Под ред. Н.Н. Моисеева. - М.: Наука, 1979. - 303с.

10. Карр Ч., Хоув Ч. Количественные методы принятия решений в управлении и экономике. М.: Мир, 1966.

11. Конюховский П.В. Математические методы исследования операций в экономике. Санкт-Петербург: ПИТЕР. 2000.

12. Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0. СПб.: BHV-Санкт-Петербург, 1997.

13. Лагоша Борис Александрович. Оптимальное управление в экономике: Учеб.пособие для вузов / Лагоша Борис Александрович. - М.: Финансы и статистика, 2003. - 192с.:

14. Лейбкинд Александр Рафаилович. Моделирование организационных структур:(Классиф. подход) / Лейбкинд Александр Рафаилович, Б. Л. Рудник. - М.: Hаука, 1981. - 143с.

15. Моделирование межотраслевых взаимодействий / Отв. ред. Ю.В.Яременко. - М.: Наука, 1984. - 278с.:

16. Моделирование народнохозяйственных процессов: Учеб. пособие / Под ред. И.В.Котова. - 2-е изд.; испр. и доп. - Л.: Изд-во ЛГУ, 1990. - 288с.

17. Моделирование народнохозяйственных процессов: Учеб.пособие для экон.вузов и фак. / Под ред.В.С.Дадаяна. - М.: Экономика, 1973. - 479с.

18. Монахов Андрей Васильевич. Математические методы анализа экономики: Учеб.пособие / Монахов Андрей Васильевич. - СПб.: Питер, 2002. - 176с.:

19. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр: Учеб. пособие для ун-тов. М.: Высшая школа, Книжный дом Университет, 1998.

20. Самарский А.А., Михайлов А.П. Математическое моделирование. М.: Наука. Физматлит. 1997.

21. Симкина Любовь Георгиевна. Микроэкономика: Учеб. / Симкина Любовь Георгиевна, Б. В. Корнейчук; Л.Г.Симкина,Б.В.Корнейчук. - СПб.: Питер, 2002. - 464с.

22. Солодовников А.С., Браилов А.В. Линейное программирование. Учебное пособ. по курсу Математика в экономике. М.: Финансовая академия при Правительстве РФ. 1996.

23. Таха Х.А. Введение в исследование операций. Т. 2. М.: Мир, 1985.

24. Федосеев Владлен Валентинович. Экономико-математические методы и модели в маркетинге: Учеб.пособие / Федосеев Владлен Валентинович. - М.: Финстатинформ, 1996. - 112с.

25. Федосеев В.В. и др. Экономико-математические методы и прикладные модели. М.: «ЮНИТИ», 1999.

26. Фомин Г.П. Системы и модели массового обслуживания в коммерческой деятельности. Учебное пособие. М.: Финансы и статистика. 2000.

27. Холод Н.И. и др. Экономико-математические методы и модели. Под редакцией А.В. Кузнецова. М.: БГЭУ, 1999.

28. Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе. М.: «ЮНИТИ», 2000.

29. Шикин Евгений Викторовичэ Математические методы и модели в управлении: Учеб.пособие / Шикин Евгений Викторович, А. Г. Чхартишвили. - М.: Дело, 2002. - 440с.

Дополнительная литература:

1. Бабайцев В.А. и др. Математика в экономике. Линейная алгебра. (Руководство к решению задач) М.: Финансовая академия при Правительстве РФ. 1996. Часть 1.

2. Багриновский Кирилл Андреевич. Имитационные модели в народохозяйственном планировании / Багриновский Кирилл Андреевич, H. Е. Егорова, В. В. Радченко. - М.: Экономика, 1980. - 199с.

3. Базилевич Леонид Анатольевич. Моделирование организационных структур / Базилевич Леонид Анатольевич; Под ред. В.Р. Окорокова. - Л.: Изд-во ЛГУ, 1978. - 159с.

4. Белоусов Е.Г. и др. Математическое моделирование экономических процессов. М.: Изд-во МГУ, 1990.

5. Варфоломеев Валентин Иванович. Алгоритмическое моделирование элементов экономических систем.Практикум: Учеб.пособие для вузов / Варфоломеев Валентин Иванович. - М.: Финансы и статистика, 2000. - 208с.:

6. Дубров Абрам Моисеевич. Моделирование рисковых ситуаций в экономике и бизнесе: Учеб.пособие / Дубров Абрам Моисеевич, Б. А. Лагоша, Е. Ю. Хрусталев; Под ред.Б.А.Лагоши. - М.: Финансы и статистика, 2000. - 176с.

7. Иозайтис В.С., Львов Ю.А. Экономико-математическое моделирование производственных систем. М.: Высш. Шк., 1991.

8. Клейнен Дж. Статистические методы в имитационном моделировании: Пер. с англ. Вып.1 / Клейнен Дж.; Под ред.Ю.П.Адлера,В.Н.Варыгина. - М.: Статистика, 1978. - 221с.

9. Колемаев В.А. Математическая экономика. М.: «ЮНИТИ», 1998.

10. Коршунова Н., Плясунов В. Математика в экономике. М.: «ВИТА-Пресс», 1996.

11. Кремер Н.Ш. и др. Исследование операций в экономике. М.: «Банки и биржи» Изд. об. «ЮНИТИ». 1997.

12. Математические методы в макро- и микроэкономике. Минск, БГЭУ, 1997.

13. Рабинович М.Г. Многокритериальные задачи оптимизации и их применение в планировании производства. Л.: ЛИЗИ, 1986.

14. Симкина Любовь Георгиевна. Микроэкономика: Учеб. / Симкина Любовь Георгиевна, Б. В. Корнейчук; Л.Г.Симкина,Б.В.Корнейчук. - СПб.: Питер, 2002. - 464с.

15. Сио К.К. Управленческая экономика.Текст,задачи и краткие примеры: Учеб.;Пер.с англ. / К. К. Сио. - М.: ИНФРА-М, 2000. - 671с.

16. Содовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. Часть 1. М.: Финансы и статистика. 1998.

17. Справочник по математике для экономистов. /под ред. проф. В.И. Ермакова. М.: Высшая школа. 1997.

18. Черемных Ю.Н. Анализ поведения траекторий динамики народно-хозяйственных моделей / Ю. Н. Черемных. - М.: Наука, 1982. - 177с.

19. Чураков Евгений Петрович. Математические методы обработки экспериментальных данных в экономике: Учеб.пособие для вузов / Чураков Евгений Петрович. - М.: Финансы и статистика, 2004. - 240с.

Скачать архив с текстом документа