Методические указания по выполнению контрольных работ для студентов-заочников специальности
СОДЕРЖАНИЕ: Сопротивление материалов: Методические указания / Белорусская государственная сельскохозяйственная академия; Сост. В. И. Ж е-л я з к о, В. В. Д я т л о в, Л. И. М е л ь н и к о в а. Горки, 2006. 36 сМИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА
И ПРОДОВОЛЬСТВИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ, НАУКИ И КАДРОВ
УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
«БЕЛОРУССКАЯ ГОСУДАРСТВЕННАЯ
СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ»
![]()
Кафедра гидравлики и строительной механики
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ
КОНТРОЛЬНЫХ РАБОТ
Для студентов-заочников специальности
1-74 06 01 – техническое обеспечение процессов сельскохозяйственного производства
Горки 2006
Одобрено методической комиссией факультета механизации сельского хозяйства
Составили: В.И. ЖЕЛЯЗКО, В.В. ДЯТЛОВ, Л.И. МЕЛЬНИКОВА
Содержание
| Введение |
3 |
| 1. Программа изучения дисциплины |
6 |
| 2. Задачи контрольных работ |
10 |
| 3. Контрольные вопросы |
34 |
УДК 620.178.6
Сопротивление материалов : Методические указания / Белорусская государственная сельскохозяйственная академия; Сост. В. И. Ж е-л я з к о, В. В. Д я т л о в, Л. И. М е л ь н и к о в а. Горки, 2006. 36 с.
Приведены программа дисциплины, порядок решения задач и оформления контрольных работ, а также контрольные вопросы по основным темам курса «Сопротивление материалов».
Для студентов-заочников специальности 1-74 06 01 – техническое обеспечение процессов сельскохозяйственного производства.
Рецензент доцент
Составление. В.И. Желязко, В.В. Дятлов,
Л.И. Мельникова, 2006
Учреждение образования
«Белорусская государственная
сельскохозяйственная академия», 2006
ВВЕДЕНИЕ
Данные указания и задания для контрольных работ подготовлены в соответствии с типовой учебной программой дисциплины «Сопротивление материалов» для студентов высших сельскохозяйственных учебных заведений инженерных специальностей.
Контрольные работы содержат 10 задач по следующим темам:
1.Исследование напряженно-деформированного состояния в прямом стержне при растяжении (сжатии).
2. Исследование напряженно-деформированного состояния в точке.
3. Определение геометрических характеристик поперечных сечений.
4. Расчет статически определимых балок при изгибе.
5. Расчет вала круглого поперечного сечения на прочность и жесткость при кручении.
6. Сложное нагружение. Расчет вала на прочность при изгибе с кручением.
7. Внецентренное растяжение (сжатие) короткого стержня.
8. Расчет статически неопределимых систем при изгибе методом сил.
9. Продольный изгиб. Расчет прямого стержня на устойчивость.
10. Динамические напряжения. Проверка прочности упругих систем при ударе.
В соответствии с рабочими учебными планами студенты заочной формы обучения специальности 1-74 06 01 – техническое обеспечение процессов сельскохозяйственного производства выполняют две контрольные работы. Первая контрольная работа включает задачи 1–5, вторая – 6–10.
В случае если рабочим учебным планом предусмотрена одна контрольная работа, то она включает задачи 1,4, 6, 8, 9, 10.
Основным видом занятий студентов заочной формы обучения является самостоятельная работа с учебной, справочной и другой нормативной литературой.
Изучение дисциплины рекомендуется вести по темам. Для лучшего усвоения материала следует составлять конспект. После разбора материала в учебнике рекомендуется решить задачи по данной теме и ответить на контрольные вопросы, выполнить контрольное задание по изученной теме.
Контрольные работы необходимо выполнить в соответствии с личным шифром, который соответствует трем последним цифрам номера зачетной книжки. Например, при номере зачетной книжки 95-5316 шифром будет число 316. Далее обозначают первую цифру буквой «а», вторую – «б» и третью – «в» (в примере а – 3, б – 1, в – 6). Затем из таблицы каждого вертикального столбца, обозначенного внизу буквами «а», «б», «в», выбирается число, стоящее в той горизонтальной строке, номер которой совпадает со значением буквы. в примере при букве «а» надо взять число из третьей строки, при «б» – из первой, а при «в» – из шестой.
Контрольную работу следует выполнять в отдельной тетради с полями, оставленными для замечаний рецензента. На обложке тетради должны быть четко написаны: номер контрольной работы, название дисциплины, фамилия, имя, отчество студента, название факультета и специальности, учебный шифр, точный почтовый адрес. Страницы тетради нумеруются.
Решение каждой задачи следует начинать с новой страницы. Перед выполнением задания необходимо записать условие, исходные данные, выбранные в соответствии с вариантом, вычертить расчетную схему в масштабе, с указанием всех размеров, числовых данных и осей, используемых в расчете. Нагрузки на расчетной схеме необходимо показать в соответствии с их действительными направлениями.
При выполнении задания сначала следует наметить ход решения, указать те допущения, которые могут быть положены в его основу, а затем произвести расчет. При этом все необходимые вычисления по возможности сначала проделать в общем виде, обозначив все данные и искомые величины буквами, а затем вместо буквенных обозначений поставить числовые значения и найти результат. Расчеты следует выполнять последовательно, теоретически обоснованно с необходимыми пояснениями и достаточно подробно. При выполнении расчетов нужно указывать литературу с отметкой страниц, таблиц, графиков, откуда взяты расчетные формулы и другие величины справочного характера.
Все расчеты должны производиться в единицах СИ. Эпюры необходимо вычерчивать под расчетной схемой на одной странице с указанием размерности и всех характерных координат. Вычисления следует вести с обычной в технических расчетах точностью (до трех значащих цифр после запятой).
В конце контрольной работы необходимо привести список использованной литературы, поставить дату выполнения и личную подпись.
После рецензирования контрольной работы на кафедре в соответствии с замечаниями рецензента необходимо внести требуемые исправления, которые выполняют в конце тетради на чистых листах после заголовка «Исправления к контрольной работе».
Работы, оформленные небрежно, а также выполненные не по своему варианту, не рассматриваются и не засчитываются, и возвращаются для переделки.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
О с н о в н а я
1.Ф е о д о с ь е в В. И. Сопротивление материалов. М.: Наука, 1986.
2. Д а р к о в А. В., Ш п и р о Г. С. Сопротивление материалов. М.: Высшая школа, 1975 и последующие издания.
3. П о д с к р е б к о М. Д. Сопротивление материалов. – Мн.: Дизайн ПРО, 1998.
Д о п о л н и т е л ь н а я
4. Б е л я е в Н. М. Сопротивление материалов. М.: Наука, 1976.
5. Т а т у р Г. К. Общий курс сопротивления материалов. Мн.: Вышэйшая школа, 1974.
6. Ф е о д о с ь е в В. И. Десять лекций-бесед по сопротивлению материалов. М.: Наука, 1975.
7. Сборник задач по сопротивлению материалов /Под ред. проф. В.К. Качурина, М.: Наука, 1970.
8. В и н о к у р о в Е. Ф., П е т р о в и ч А. Г., Ш е в ч у к Л. И. Сопротивление материалов. Расчетно-проектировочные работы: Учебное пособие для вузов. Мн.: Вышэйшая школа, 1987.
9. С т е п и н П. А. Сопротивление материалов. – М.: Высшая школа, 1979.
10. П и с а р е н к о Г. С., А г а р е в В. А., К в и т к а А. Л. и др. Сопротивление материалов. – Киев: Вища школа, 1979.
11. Пособие к решению задач по сопротивлению материалов. И. Н. М и р о л ю-б о в и др. – М.: Высшая школа, 1985.
12. И ц к о в и ч Г. М. Сопротивление материалов. – М.: Высшая школа, 1999.
13. Сопротивление материалов. Учеб. Пособие / Под ред. Н. А. К о с т е н к о. – М.: Высшая школа, 2000.
1. ПРОГРАММА ИЗУЧЕНИЯ ДИСЦИПЛИНЫ
Общие понятия. Задачи курса «Сопротивление материалов» по изучению напряженно деформированного состояния и работоспособности наиболее простых и типичных элементов конструкций, машин, приборов.
Связь курса с общенаучными, общеинженерными и специальными дисциплинами. Сопротивление материалов, теория упругости и пластичности. Методика решения задач в сопротивлении материалов. Принципы выбора расчетных схем. Однородная сплошная среда. Упругость и пластичность. Понятие об изотропии и анизотропии. Определение стержня, пластины и оболочки. Перемещения угловые и линейные. Перемещения малые и большие. Принцип начальных размеров. Деформации линейные и угловые. Понятия о больших деформациях. Внешние силы и их классификация. Силы объемные и поверхностные. Заданные нагрузки и реакции опор. Нагрузки статические и динамические. Нагрузки постоянные и переменные во времени. Основные гипотезы сопротивления материалов о свойствах конструкционных материалов. Внутренние силы. Метод сечений. Напряжение полное, нормальное и касательное. Внутренние силовые факторы в поперечных сечениях и их выражение через напряжения. Классификация типов нагружения стержня по внутренним силовым факторам.
Л и т е р а т у р а: [1, введение]; [2, гл.1]; [3, гл.1].
Растяжение и сжатие . Построение эпюр продольных сил. Напряжения в поперечных сечениях стержня. Закон Гука, коэффициент Пуассона. Жесткость при растяжении и сжатии. Потенциальная энергия упругой деформации.
Диаграмма растяжения малоуглеродистой стали и ее характерные параметры. Истинная диаграмма напряжения. Разгрузка и повторное нагружение. Пластическое и хрупкое разрушение материала. Характеристики пластических свойств материалов. Диаграмма сжатия. Предельное состояние. Критерии предельного состояния в зависимости от свойства материала, условий работы и назначения конструкции. Расчет по допускаемым напряжениям и нагрузкам. Коэффициенты безопасности (запаса прочности). Типы задач при расчете на прочность: проверка прочности, подбор сечений и определение допускаемой нагрузки. Расчеты на жесткость. Расчет простейших статически неопределимых систем при растяжении и сжатии.
Л и т е р а т у р а: [1, гл.1]; : [2, гл.2]; : [3, гл.2, 3]; : [6, гл.1].
Теория напряженного и деформированного состояний. Напряженное состояние в точке. Виды напряженного состояния. Линейное напряженное состояние. Плоское напряженное состояние. Закон парности касательных напряжений. Главные площадки и главные напряжения. Экстремальные значения касательных напряжений. Чистый сдвиг как частный случай плоского напряженного состояния. Закон Гука для сдвига. Модуль сдвига. Связь между упругими постоянными для изотропного тела. Понятие об объемном напряженном состоянии. Обобщенный закон Гука. Удельная потенциальная энергия упругой деформации. Удельная энергия изменения объема и удельная энергия изменения формы.
Л и т е р а т у р а: [1, гл.7]; : [2, гл.3]; : [6, гл.2,].
Теории прочности. Назначение гипотез прочности. Эквивалентное напряжение. Гипотезы прочности для пластического состояния материала. Критерии текучести: наибольших касательных напряжений и энергии изменения формы. Сопоставление критериев с опытными данными. Критерий хрупкого разрушения (критерий Мора).
Л и т е р а т у р а: [1, гл.8]; : [2, гл.8]; : [3, гл.7].
Экспериментальные методы исследования деформации и напряжения. Измерение деформаций механическими тензометрами. Основы электротензометрии. Тензорезисторы (датчики омического сопротивления). Схема измерения и аппаратура. Понятие о поляризационно-оптическом методе исследования напряжений. Схема прибора. Краткие сведения о других экспериментальных методах (метод сеток, метод хрупких лаковых покрытий, метод муаровых полос).
Л и т е р а т у р а: [1, гл.14].
Геометрические характеристики поперечных сечений бруса. Статические моменты сечений. Определение центра тяжести сечения. Осевые, полярный и центробежный моменты инерции сечения. Общие свойства моментов инерции. Изменение моментов инерции при параллельном переносе и повороте осей. Главные оси и главные моменты инерции. Определение расположения главных центральных осей и вычисление главных моментов инерции различных сечений. Радиусы инерции.
Л и т е р а т у р а: [1, гл.3]; : [2, гл.5]; : [3, гл.12,].
Кручение. Кручение прямого стержня круглого поперечного сечения. Напряжения в поперечном сечении. Угол закручивания. Главные напряжения. Потенциальная энергия упругой деформации при кручении. Расчет на прочность и жесткость вала круглого кольцевого поперечного сечения. Статически неопределимые задачи на кручение. Основные результаты теории кручения стержня некруглого поперечного сечения. Расчет цилиндрических винтовых пружин с малым шагом витков.
Л и т е р а т у р а: [1, гл.2]; : [2, гл.6]; : [3, гл.9,].
Изгиб. Классификация видов изгиба. Типы опор. Определение внутренних силовых факторов в поперечных сечениях балок (поперечная сила и изгибающий момент). Построение эпюр внутренних силовых факторов. Дифференциальные зависимости при изгибе. Контроль правильности построения эпюр. Нормальные напряжения при изгибе. Расчеты на прочность при изгибе. Рациональные формы поперечного сечения при изгибе. Рациональные формы поперечного сечения балок. Касательные напряжения при изгибе. Перемещения при изгибе. Дифференциальное уравнение изогнутой оси балки и его интегрирование. Метод начальных параметров.
Л и т е р а т у р а: [1, гл.4]; : [2, гл.7]; : [3, гл.10, 11,13].
Сложное нагружение. Косой изгиб. Нормальные напряжения при косом изгибе. Положение нейтральной оси и опасных точек в сечении. Определение прогибов. Внецентренное растяжение или сжатие стержня. Нахождение опасных сечений и точек. Ядро сечения. Изгиб с кручением брусьев круглого поперечного сечения.
Л и т е р а т у р а: [1, гл.4, 35, 36]; : [2, гл.9]; : [6, гл.20,22].
Основы расчета на прочность при напряжениях, переменных во времени. Современные представления о прочности материалов при переменных напряжениях. Механизм усталостного разрушения. Параметры цикла напряжений. Кривые усталости и предел выносливости. Диаграмма предельных амплитуд. Факторы, влияющие на усталостную прочность. Порядок расчета на прочность при переменных напряжениях. Определение коэффициента запаса. Формула Серенсена-Канисошвили. Коэффициент запаса прочности при совместном действии изгиба и кручения.
Л и т е р а т у р а: [1, гл.11]; : [2, гл.15].:
Определение перемещений и расчет статически неопределимых систем. Потенциальная энергия упругой деформации бруса при произвольном нагружении. Теорема о взаимности работ. Интеграл Мора, его вычисление по способу Верещагина. Метод сил. Выбор рациональной основной системы. Статическая и деформационная проверки. Определение перемещений.
Л и т е р а т у р а: [1, гл.5,6]; : [2, гл.11, 12]; : [3, гл.15,].
Продольный изгиб прямого стержня. Понятие об устойчивых и неустойчивых формах равновесия. Критическая сила. Формула Эйлера при различных случаях опорных закреплений и пределы ее применимости. Формула Ясинского. Расчет по коэффициенту снижения допускаемых напряжений. Рациональные формы поперечных сечений сжатых стержней. Энергетический метод определения критических нагрузок.
Л и т е р а т у р а: [1, гл.12]; : [2, гл.13]; : [3, гл.27].
Расчет тонкостенных осесимметричных оболочек и толстостенных цилиндров. Безмоментная теория осесимметрично нагруженных тонкостенных оболочек вращения. Уравнение Лапласа. Расчет сферических сосудов и цилиндрических резервуаров, находящихся под действием постоянного и гидростатического давления.
Задача Ламе. Применение формул Ламе к расчету толстостенных цилиндров, нагруженных внутренним и наружным давлениями.
Л и т е р а т у р а: [1, гл.9]; : [2, гл.16]; : [3, гл.25,].
Изгиб плоского бруса большой кривизны. Внутренние силовые факторы. Нормальные напряжения в поперечных сечениях бруса большой кривизны. Определение положения нейтральной оси при чистом изгибе.
Л и т е р а т у р а: [1, гл.4 §37]; : [2, гл.10]; : [3, гл.25,].
Динамическая нагрузка. Типы динамических нагрузок. Учет сил инерции. Элементарная теория удара. Динамический коэффициент при вертикальном, наклонном и горизонтальном ударах. Защита приборов и оборудования от удара. Колебания невесомых упругих систем с одной степенью свободы. Свободные и вынужденные колебания. Резонанс. Основные средства борьбы с вибрациями деталей машин и элементов конструкций.
Л и т е р а т у р а: [1, гл.13]; : [2, гл.14]; : [3, гл.29,30].
1. ЗАДАЧИ КОНТРОЛЬНЫХ РАБОТ
Задача 1. Ступенчатый стальной стержень, имеющий продольные размеры 1 , 2 , 3 и площади поперечных сечений А1 , А2 , А3 , нагружен по оси продольными силами F.
Требуется:
1) определить продольные усилия, нормальные напряжения и перемещения в поперечных сечениях стержня под действием внешних сил F, установить опасное сечение и проверить прочность из условия, что расчетное сопротивление R = 210 МПа;
2) построить эпюры продольных усилий, нормальных напряжений и перемещений в поперечных сечениях стержня под действием внешних сил F;
3) определить продольные усилия, нормальные напряжения и перемещения в сечениях стержня под влиянием изменения температуры без учета внешних сил F и построить эпюры.
Числовые значения для решения задачи 1 принять по табл.1, а расчетную схему – по рис.1.
Перед тем как приступить к решению задачи, необходимо изучить разделы «Общие понятия» и «Растяжение и сжатие».
Решение задач следует начать с проверки возможности перекрытия зазора D в одной из заделок стержня под действием системы сил F. Для этого отбрасывается одна опора и находится удлинение стержня D как статически определимого. Если удлинение D меньше зазора D, стержень решается как статически определимый. В противном случае одностержневая система является статически неопределимой. Для раскрытия статической неопределимости следует отбросить одну заделку, заменив ее неизвестной опорной реакцией. Значение этой реакции определяется путем составления уравнения совместности деформаций и решения его. Аналогично находится и вторая неизвестная реакция. Для проверки правильности определения реакций составляется уравнение статики.
Внутренние усилия определяются с использованием метода сечений. Эпюры вычерчиваются против расчетной схемы карандашом. При этом растягивающие усилия положительны (+) и откладываются справа от базовой линии эпюры, а сжимающие – отрицательны (–) и откладываются слева.
Примеры решения задачи приведены в [2, c.73…84] и [8,с.9…32].
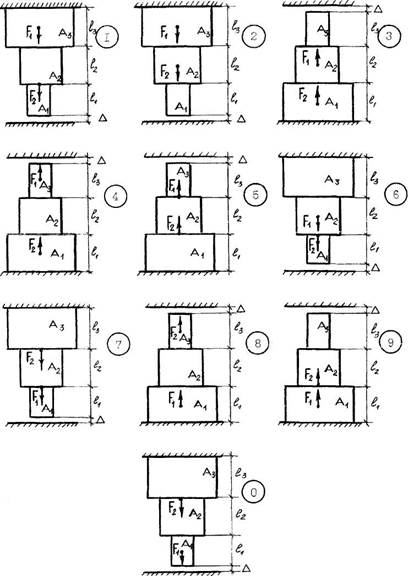
Рис. 1. Расчетные схемы к задаче 1.
Т а б л и ц а 1. Числовые данные к задаче 1.
| Номер строки |
Номер схемы |
F1 , кН |
F2 , кН |
A1 |
A2 |
A3 |
1 |
2 |
3 |
Dt |
D |
| см2 |
м |
С |
мм |
||||||||
| 1 |
0 |
160 |
50 |
4 |
8 |
6 |
0,40 |
0,80 |
0,50 |
55 |
0,11 |
| 2 |
1 |
200 |
70 |
5 |
9 |
4 |
0,45 |
0,75 |
0,70 |
64 |
0,12 |
| 3 |
2 |
190 |
90 |
6 |
10 |
7 |
0,50 |
0,70 |
0,30 |
72 |
0,13 |
| 4 |
3 |
150 |
140 |
7 |
11 |
8 |
0,42 |
0,76 |
0,80 |
49 |
0,14 |
| 5 |
4 |
140 |
170 |
8 |
12 |
16 |
0,52 |
0,74 |
0,60 |
61 |
0,15 |
| 6 |
5 |
130 |
160 |
9 |
13 |
12 |
0,78 |
0,90 |
0,42 |
68 |
0,16 |
| 7 |
6 |
60 |
220 |
10 |
7 |
13 |
0,30 |
0,85 |
0,48 |
75 |
0,17 |
| 8 |
7 |
90 |
240 |
11 |
6 |
11 |
0,60 |
0,68 |
0,72 |
53 |
0,18 |
| 9 |
8 |
80 |
210 |
12 |
5 |
9 |
0,62 |
0,54 |
0,64 |
63 |
0,19 |
| 0 |
9 |
70 |
230 |
13 |
4 |
5 |
0,64 |
0,40 |
0,62 |
70 |
0,10 |
| ххх |
в |
б |
а |
а |
б |
а |
в |
б |
а |
в |
в |
Задача 2. Элементарный параллелепипед, вырезанный из упругого тела, находится под действием сил, создающих плоское напряженное состояние (одно из трех главных напряжений равно нулю).
Требуется:
1) определить главные напряжения и направления главных площадок;
2) найти максимальные касательные напряжения;
3) определить относительные деформации и относительное изменение объема;
4) установить удельную потенциальную энергию деформаций.
Числовые значения для решения задачи 2 принять по табл.2, а расчетную схему – по рис. 2.
Т а б л и ц а 2. Числовые данные к задаче 2.
| Номер строки |
Номер схемы |
sх , МПа |
sу , МПа |
tху , МПа |
Модуль Е, МПа |
Коэффициент Пуассона, h |
| 1 |
0 |
90 |
50 |
10 |
1,0105 |
0,16 |
| 2 |
1 |
80 |
60 |
20 |
1,2105 |
0,18 |
| 3 |
2 |
70 |
70 |
30 |
1,3105 |
0,20 |
| 4 |
3 |
60 |
80 |
40 |
1,4105 |
0,22 |
| 5 |
4 |
50 |
90 |
50 |
1,5105 |
0,24 |
| 6 |
5 |
40 |
100 |
60 |
1,6105 |
0,25 |
| 7 |
6 |
30 |
40 |
70 |
1,7105 |
0,26 |
| 8 |
7 |
20 |
30 |
60 |
1,8105 |
0,27 |
| 9 |
8 |
100 |
20 |
50 |
1,9105 |
0,28 |
| 0 |
9 |
10 |
110 |
40 |
2,0105 |
0,30 |
| ххх |
в |
б |
а |
в |
б |
а |
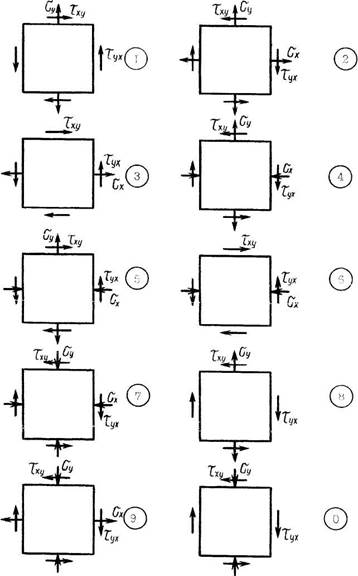
Рис. 2. Расчетные схемы к задаче 2.
Перед тем как приступить к решению задачи, необходимо изучить раздел «Теория напряженного и деформированного состояний». Решение задачи следует начать с установления знаков исходных напряжений. Правило знаков для этих напряжений принимается следующим: растягивающие нормальные напряжения считаются положительными, сжимающие – отрицательными. Касательные напряжения положительны, если обход контура по их направлению происходит по часовой стрелке, если наоборот – отрицательные.
Примеры решения задачи приведены в [2, с.114…118] и [8, c.44…55].
Задача 3. Дано составное сечение из стальных прокатных профилей по ГОСТ 8509–72, ГОСТ 8510–72, ГОСТ 8239 –72, ГОСТ 8240–72, форма которого приведена на рис. 3.
Требуется:
1) определить координаты центра тяжести;
2) вычислить осевые и центробежный моменты инерции относительно центральных осей;
3) определить положение главных центральных осей и величины главных центральных моментов инерции;
4) найти главные радиусы инерции и построить эллипс инерции.
Числовые значения для решения задачи 3 принять по табл.3, а расчетную схему – по рис. 3.
Т а б л и ц а 3. Числовые данные к задаче 3.
| Номер строки |
Номер схемы |
Двутавр |
Швеллер |
Уголок равнопо- лочный |
Уголок неравно- полочный |
Пластина, b x h, см |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 1 |
0 |
24а |
16 |
10 |
10/6,3 |
16х2 |
| 2 |
1 |
24 |
18а |
11 |
11/7 |
18х2 |
| 3 |
2 |
22а |
20 |
12.5 |
12.5/8 |
20х2 |
| 4 |
3 |
20 |
16а |
14 |
16/10 |
16х2 |
| 5 |
4 |
18а |
18а |
18 |
9/5,6 |
18х2 |
| 6 |
5 |
20а |
20а |
16 |
14/9 |
20х2 |
| 7 |
6 |
22 |
24 |
20 |
18/11 |
16х2 |
| 8 |
7 |
18 |
24а |
25 |
11/7 |
18х2 |
| 9 |
8 |
27 |
27 |
22 |
16/10 |
20х2 |
| 0 |
9 |
27а |
22 |
20 |
20/12.5 |
16х2 |
| ххх |
в |
б |
а |
в |
б |
а |
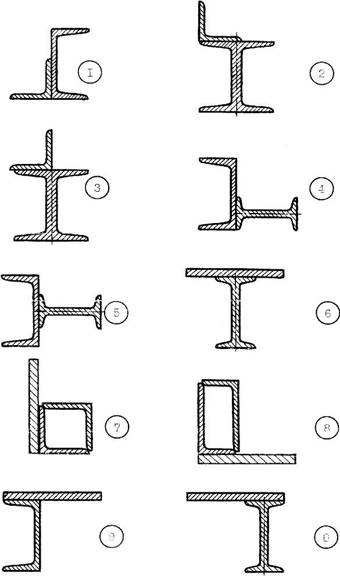
Рис. 3. Расчетные схемы к задаче 3.
Перед тем, как приступить к решению задачи, необходимо изучить раздел «Геометрические характеристики поперечных сечений».
Решение задачи следует начать с выбора из сортамента прокатных профилей всех размеров и геометрических характеристик отдельных элементов составного сечения. Составное сечение следует вычертить в масштабе на миллиметровой бумаге с указанием всех размеров и положений собственных центральных осей элементов сечения. Далее следует выбрать первоначальную систему координат. Во избежание ошибок рекомендуется систему координат выбирать таким образом, чтобы все составное сечение находилось в положительном квадранте. После этого следует определить координаты центра тяжести составного сечения. При этом центр тяжести составного сечения должен быть расположен на прямой, соединяющей центры тяжести составных элементов. Затем вычисляются моменты инерции составного сечения, определяется положение главных центральных осей.
Положение главной центральной оси U, относительно которой момент инерции максимален (Iu = Imax ), можно определить двумя способами.
1. При Iху 0 главная ось U проходит через 1-й и 3-й, а при Iху 0 – через 2-й и 4-й квадранты.
2. Если Ix Iу , то главная ось U находится под углом a к оси X. При Iу Ix ось U находится под углом a к оси Y.
Примеры решения задачи приведены в [2, c.160…163] и [8, c.67…75].
Задача 4. Балка одинаковой жесткости по длине (ЕI = const) нагружена сосредоточенной силой F, распределенной нагрузкой q и моментом М.
Требуется:
1) для расчетной схемы «А» построить эпюры поперечных сил и изгибающих моментов и подобрать двутавровое сечение балки;
2) для расчетной схемы «В» построить эпюры поперечных сил и изгибающих моментов, подобрать прямоугольное сечение балки с соотношение сторон 1:2 и построить эпюры нормальных и касательных напряжений в опасном сечении балки.
Числовые значения для решения задачи 4 принять по табл. 4, а расчетную схему – по рис. 4 и 5.
Перед тем как приступить к решению задачи необходимо изучить раздел «Изгиб».
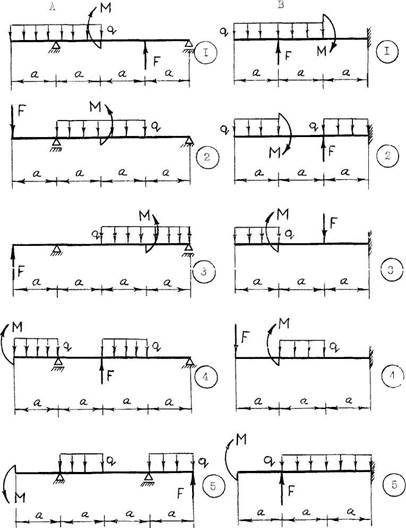
Рис. 4. Расчетные схемы к задаче 4.
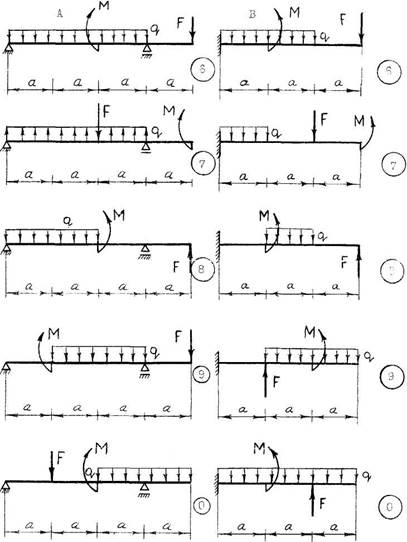
Рис. 5. Расчетные схемы к задаче 4.
Т а б л и ц а 4. Числовые данные к задаче 4.
| Номер строки |
Номер схемы |
Расстояние а, м |
F, кН |
q, кН/м |
М кНм |
Допускаемое значение напряжения [s], МПа |
|
| Схема А |
Схема В |
||||||
| 1 |
0 |
0,50 |
20 |
11 |
15 |
160 |
10 |
| 2 |
1 |
0,60 |
22 |
12 |
20 |
165 |
15 |
| 3 |
2 |
0,70 |
24 |
13 |
25 |
170 |
20 |
| 4 |
3 |
0,65 |
25 |
15 |
10 |
175 |
25 |
| 5 |
4 |
0,75 |
26 |
17 |
24 |
180 |
30 |
| 6 |
5 |
0,90 |
18 |
16 |
30 |
185 |
35 |
| 7 |
6 |
0,80 |
16 |
14 |
22 |
190 |
40 |
| 8 |
7 |
0,95 |
15 |
18 |
16 |
195 |
45 |
| 9 |
8 |
1,00 |
14 |
20 |
18 |
200 |
50 |
| 0 |
9 |
0,55 |
23 |
19 |
26 |
210 |
55 |
| ххх |
в |
б |
а |
в |
б |
а |
в |
Решение задачи (расчетная схема А) следует начать с определения опорных реакций. Для этого следует составить два независимых уравнения статики в виде М = 0. После определения реакций должна быть выполнена проверка правильности расчетов. При этом рекомендуется использовать уравнение статики вида Fу = 0. Если реакции определены верно, то, используя метод сечений, находят внутренние силовые факторы Q и М.
Для расчетной схемы В опорные реакции можно не определять, а сразу приступать к определению внутренних силовых факторов Q и М, используя метод сечений, начиная со свободного конца консольной балки. Эпюры Q и М необходимо строить под расчетными схемами балок.
Для контроля правильности построения эпюр следует руководствоваться следующими основными положениями. На участках балки, где отсутствует распределенная нагрузка q, поперечные силы постоянны, а изгибающие моменты меняются по линейному закону. Скачки на эпюре Q соответствуют точкам приложения сосредоточенных сил, в том числе и опорных реакций. Скачок на эпюре М соответствует действию сосредоточенного внешнего момента М. На участках, где приложена постоянная распределенная нагрузка q, поперечная сила изменяется по длине балки по линейному закону, а эпюра изгибающих моментов на этом участке ограничена квадратной параболой, вогнутость которой соответствует направлению распределенной нагрузки q (правило «паруса»).
Примеры решения задачи приведены в [1, c.157…158], [2, c.314…3] и [8, c.93…102].
Задача 5. К стальному валу приложены три известных момента: М1 , М2 , М3 .
Требуется:
1) определить значение момента Х из условия, что угол поворота правого концевого сечения вала равен нулю;
2) построить эпюру крутящих моментов с учетом найденного значения момента Х;
3) подобрать диаметр вала из расчета на прочность;
4) построить эпюру углов закручивания вала;
5) найти наибольший относительный угол закручивания.
Числовые значения для решения задачи 5 принять по табл.5, а расчетную схему – по рис.6.
Т а б л и ц а 5. Числовые данные к задаче 5.
| Номер строки |
Номер схемы |
М1 |
М2 |
М3 |
а |
в |
с |
[] МПа |
| Н·м |
м |
|||||||
| 1 |
0 |
600 |
1600 |
2000 |
1,0 |
1,5 |
1,0 |
45 |
| 2 |
1 |
700 |
1700 |
1900 |
1,1 |
1,6 |
1,1 |
50 |
| 3 |
2 |
800 |
1800 |
1800 |
1,2 |
1,7 |
1,2 |
55 |
| 4 |
3 |
900 |
1900 |
1700 |
1,3 |
1,8 |
1,3 |
60 |
| 5 |
4 |
1000 |
2000 |
1600 |
1,4 |
1,9 |
1,4 |
65 |
| 6 |
5 |
1100 |
600 |
1500 |
1,5 |
2,0 |
1,5 |
70 |
| 7 |
6 |
1200 |
700 |
1400 |
1,6 |
1,4 |
1,6 |
75 |
| 8 |
7 |
1300 |
800 |
1300 |
1,7 |
1,3 |
1,7 |
80 |
| 9 |
8 |
1400 |
900 |
1200 |
1,8 |
1,2 |
1,8 |
40 |
| 0 |
9 |
1500 |
1000 |
1100 |
1,9 |
1,1 |
1,9 |
35 |
| ххх |
в |
в |
б |
а |
в |
б |
а |
в |
Перед тем как приступить к решению задачи необходимо изучить раздел «Кручение».
При определении неизвестного момента Х следует рассмотреть деформацию вала под действием внешних моментов. Для этого необходимо составить уравнение углов закручивания вала, используя принцип независимости действия сил. При этом угол поворота правого концевого вала по условию задачи должен равняться нулю. После определения неизвестного значения Х, используя метод сечений, следует

Рис. 6. Расчетные схемы к задаче 5.
построить эпюру крутящих моментов Мкр . По наибольшему значению крутящего момента выбрать опасное сечение вала. из условия прочности по заданному касательному напряжению [] подобрать диаметр вала, округлив расчетное значение до ближайшего стандартного: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 120, 125, 130 и т.д. мм. Затем необходимо построить эпюру углов закручивания и найти наибольший относительный угол закручивания.
Примеры решения задачи приведены в [2, c. 195…199] и [8, c.85…89].
Задача 6. Шкив с диаметром D1 и углом наклона ветвей ремня к горизонту 1 делает n оборотов в минуту и передает мощность N (кВт). Два других шкива имеют одинаковые диаметр D2 и углы наклона ветвей ремня к горизонту 2 и каждый из них передает мощность N/2.
Требуется:
1) определить моменты, приложенные к шкивам, по заданным N и n построить эпюру крутящих моментов Мкр ;
2) определить окружные усилия t1 и t2 , действующие на шкивы, по найденным моментам и заданным диаметрам шкивов D1 и D2 ;
3) определить нагрузки, действующие на вал, принимая их равными трем окружным усилиям;
4) определить силы, изгибающие вал в вертикальной и горизонтальной плоскостях (массу шкивов и вала не учитывать);
5) построить эпюры изгибающих моментов от горизонтальных сил Мг и от вертикальных сил Мв ;
6) построить эпюру суммарных изгибающих моментов Ми ;
7) найти опасное сечение вала и определить расчетный момент, пользуясь третьей теорией прочности;
8) подобрать диаметр вала по заданному значению [] и округлить расчетное значение до ближайшего: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 120, 125, 130 и далее через 10 мм.
Числовые значения для решения задачи 6 принять по табл. 6, расчетную схему – по рис. 7 и 8.
Перед тем как приступить к решению задачи, необходимо изучить раздел «Сложное нагружение».
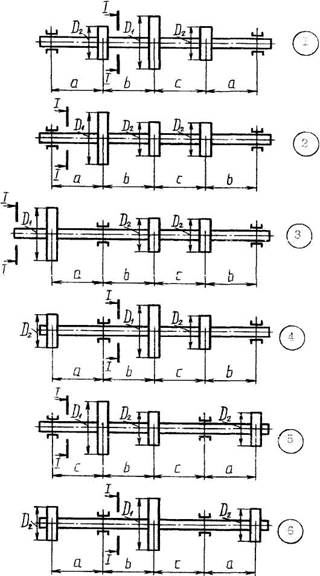
Рис. 7. Расчетные схемы к задаче 6.
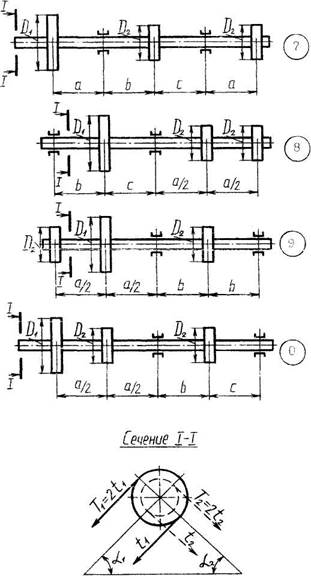
Рис. 8. Расчетные схемы к задаче 6.
Т а б л и ц а 6. Числовые данные к задаче 6 .
| Номер строки |
Номер схемы |
N, кВт |
n, об/мин |
1 |
2 |
а |
b |
c |
D1 |
D2 |
[] МПа |
| град. |
м |
||||||||||
| 1 |
1 |
100 |
900 |
10 |
0 |
1,9 |
1,0 |
1,1 |
1,5 |
0,6 |
100 |
| 2 |
2 |
110 |
800 |
20 |
90 |
1,8 |
1,1 |
1,2 |
1,4 |
0,7 |
105 |
| 3 |
3 |
120 |
700 |
30 |
80 |
1,7 |
1,2 |
1,3 |
1,3 |
0,8 |
110 |
| 4 |
4 |
130 |
600 |
40 |
70 |
1,6 |
1,3 |
1,4 |
1,2 |
0,9 |
115 |
| 5 |
5 |
140 |
500 |
50 |
60 |
1,5 |
1,4 |
1,5 |
1,1 |
1,0 |
120 |
| 6 |
6 |
150 |
400 |
60 |
50 |
1,1 |
1,5 |
1,6 |
1,0 |
1,1 |
125 |
| 7 |
7 |
115 |
300 |
70 |
40 |
1,3 |
1,6 |
1,7 |
0,9 |
1,2 |
130 |
| 8 |
8 |
125 |
200 |
80 |
30 |
1,2 |
1,7 |
1,8 |
0,8 |
1,3 |
135 |
| 9 |
9 |
135 |
100 |
90 |
20 |
1,1 |
1,8 |
1,9 |
0,7 |
1,4 |
140 |
| 0 |
10 |
145 |
100 |
0 |
10 |
1,0 |
1,9 |
1,0 |
0,6 |
1,5 |
145 |
| ххх |
в |
б |
а |
в |
б |
а |
в |
б |
а |
в |
в |
Решение задачи следует начать с определения крутящих моментов, приложенных к шкивам. Для этого рекомендуется пользоваться формулой Мкр = 9550·N/n (H·м). В этой формуле N – мощность (кВт), n– число оборотов вала (об/мин).
После определения крутящих моментов, приложенных к шкивам, строят эпюру крутящих моментов и определяют окружные усилия, действующие на шкивы. Вал подвергается изгибу под действием веса шкивов и окружных усилий, передаваемых ременными передачами. При решении задачи вес шкивов не учитывать.
Силы, которые передаются на вал через шкивы, действуют под определенными углами наклона (1 и 2 ) к горизонтальной оси, проходящей через центр тяжести шкива. Эти силы необходимо разложить на две составляющие – горизонтальную и вертикальную, построить эпюры изгибающих моментов от горизонтальных и вертикальных сил и эпюру суммарных изгибающих моментов. По эпюрам крутящих моментов и суммарной изгибающих моментов определяют опасное сечение и расчетный момент. Опасным является такое сечение вала, в котором суммарный изгибающий и крутящий моменты одновременно велики. По значению расчетного момента производится подбор диаметра вала.
Примеры решения задачи приведены в [2, c.377…384] и [7, c.289…291].
Задача 7. Короткий стальной стержень двутаврового сечения находится под действием продольной силы F, приложенной внецентренно в точке А с координатами ХF и YF .
Требуется:
1) определить положение нейтральной линии сечения;
2) определить максимально допустимое значение силы F из условия прочности по нормальным напряжениям;
3) построить эпюру нормальных напряжений в поперечном сечении стержня;
Числовые значения для решения задачи 7 принять по табл.7, а расчетную схему – по рис. 9.
«+» – сила F растягивает стержень, «–» – сжимает.
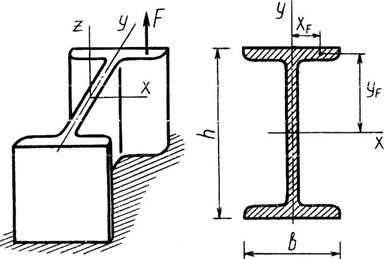
Рис. 9. Расчетные схемы к задаче 7.
Перед тем как приступить к решению задачи, необходимо изучить раздел «Сложное нагружение».
Решение задачи следует начать с того, что из сортамента прокатных профилей выписывают размеры и геометрические характеристики двутавра: h и b мм; А в см2 Iх и Iу в см4 . Координаты точки приложения силы F следует вычислить через соотношения ХF /b и YF /h. Далее необходимо определить положение нейтральной линии сечения. После этого в масштабе вычерчивается все сечение, наносится точка А приложения силы F, проводится нейтральная линия сечения и определяются опасные точки сечения для растянутой и сжатой зон. Используя условие прочности, по заданному значению [] определяется максимально допустимое значение силы F. Рассчитываются нормальные напряжения, и строится эпюра.
Т а б л и ц а 7. Числовые данные к таблице 7.
| Номер строки |
Двутавр № |
Направление cилы F* |
ХF /b |
YF /h |
[] МПа |
| 1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
24а |
+ |
0,5 |
– 0,5 |
190 |
| 2 |
24 |
– |
0,4 |
– 0,5 |
185 |
| 3 |
22а |
+ |
0,3 |
– 0,5 |
180 |
| 4 |
20 |
– |
0,5 |
0,5 |
175 |
| 5 |
18а |
+ |
–0,5 |
–0,5 |
170 |
| 6 |
20а |
– |
0,3 |
0,5 |
165 |
| 7 |
22 |
+ |
–0,5 |
–0,5 |
160 |
| 8 |
18 |
– |
–0,4 |
–0,5 |
155 |
| 9 |
27 |
+ |
–0,3 |
0,5 |
150 |
| 0 |
27а |
- |
-0,5 |
0,5 |
145 |
| x хх |
в |
а |
в |
б |
в |
Примеры решения задачи приведены в [7, 271…272] и[8, c.157…162].
Задача 8. Рама с постоянной жесткостью вертикальных и горизонтальных элементов (ЕI = const), имеющая размеры L и h, нагружена в своей плоскости распределенной нагрузкой q.
Требуется:
1) установить степень статической неопределимости;
2) выбрать основную систему;
3) составить канонические уравнения;
4) построить эпюры М от единичных сил и от заданной нагрузки;
5) вычислить коэффициенты и свободные члены канонических уравнений, проверить их, решить систему и найти величины лишних неизвестных;
6) построить расчетные эпюры М, Q и N;
7) выполнить статическую проверку узлов.
Числовые значения для решения задачи 8 принять по табл. 8, а расчетную схему – по рис. 10.
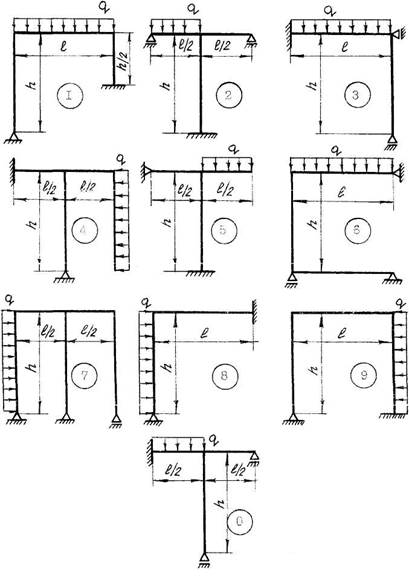
Рис. 10. Расчетные схемы к задаче 8.
Т а б л и ц а 8. Числовые данные к задаче 8.
| Номер строки |
Номер схемы |
Размеры, м |
q, кН/м |
|
|
|
h |
|||
| 1 |
2 |
3 |
4 |
5 |
| 1 |
0 |
8 |
2 |
11 |
| 2 |
1 |
6 |
3 |
12 |
| 3 |
2 |
4 |
4 |
13 |
| 4 |
3 |
5 |
5 |
15 |
| 5 |
4 |
7 |
6 |
17 |
| 6 |
5 |
9 |
7 |
16 |
| 7 |
6 |
10 |
6 |
14 |
| 8 |
7 |
11 |
5 |
18 |
| 9 |
8 |
12 |
4 |
20 |
| 0 |
9 |
8 |
3 |
19 |
| xxx |
в |
б |
а |
в |
Перед тем как приступить к решению задачи, необходимо изучить раздел «Определение перемещений и расчет статически неопределимых систем».
Задачу следует решать с использованием метода сил. Согласно этому методу расчет исходной статически неопределимой системы может быть заменен расчетом некоторой основной системы. Основная
система должна быть статически определимой, геометрически неизменяемой и полученной из исходной системы путем отбрасывания лишних связей и заменой их действием неизвестных сил Х1 . Далее составляют систему канонических уравнений. Число этих уравнений совпадает с числом неизвестных сил Х1 . Для определения коэффициентов канонических уравнений необходимо построить эпюры М от единичных сил Х1 = 1 и от внешней нагрузки q, а затем использовать перемножение эпюр по способу Верещагина. Решая систему канонических уравнений, определяем неизвестные Х1 . После этого строятся эпюры М, Q и N и выполняется статическая проверка. Статическая проверка состоит в том, что любая вырезанная из исходной системы часть (узел) должна находиться в равновесии под действием внешних сил и внутренних силовых факторов в сечениях.
Примеры решения задачи приведены в [1, c. 237…243] и [2, c.475…480].
Задача 9. Стальной стержень длиной сжимается продольной нагрузкой F.
Требуется:
1) подобрать размеры поперечного сечения стержня из условия устойчивости, пользуясь таблицей коэффициентов продольного изгиба .
2) определить критическую силу для заданного стержня и найти коэффициент запаса устойчивости.
Числовые значения для решения задачи 9 принять по табл. 9, а расчетную схему – по рис. 11.
Т а б л и ц а 9. Числовые данные к задаче 9.
| Номер строки |
Номер схемы |
Номер сечения |
F, кН |
, м |
[], МПа |
| 0 |
5 |
1 |
700 |
2,1 |
200 |
| 1 |
1 |
2 |
750 |
2,2 |
195 |
| 2 |
2 |
3 |
800 |
2,3 |
190 |
| 3 |
3 |
4 |
850 |
2,4 |
185 |
| 4 |
4 |
5 |
400 |
2,5 |
180 |
| 5 |
5 |
6 |
450 |
2,6 |
175 |
| 6 |
4 |
7 |
500 |
2,7 |
170 |
| 7 |
3 |
8 |
550 |
2,8 |
165 |
| 8 |
2 |
9 |
600 |
2,9 |
160 |
| 9 |
1 |
0 |
650 |
3,0 |
155 |
| x хх |
в |
а |
в |
б |
в |
Перед тем как приступить к решению задачи, необходимо изучить раздел «Продольный изгиб прямого стержня».
Подбор размеров поперечного сечения стержня следует производить методом последовательных приближений, предварительно задавшись коэффициентом = 0,5.
Примеры решения задачи приведены в [2, c.492…496] и [8, c.178…183].
Задача 10 . На двутавровую балку по ГОСТ 8239 – 72 с высоты Н падает груз F. Массу балки не учитывать.
Требуется:
1) проверить прочность материала балки;
2) определить динамическое перемещение точки приложения груза;
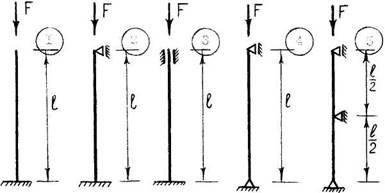
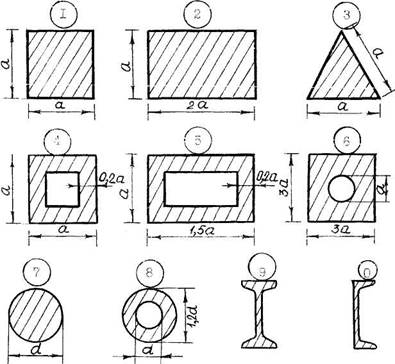
Рис. 11. Расчетные схемы к задаче 9.
3) определить максимальное нормальное напряжение в балке при условии, что правая опора заменена пружиной, податливость которой равна .
Числовые значения для решения задачи 10 принять по табл. 10, а расчетную схему – по рис. 12.
Перед тем как приступить к решению задачи, необходимо изучить раздел «Динамическая нагрузка».
Т а б л и ц а 10. Числовые данные к задаче 10.
| Номер строки |
Номер схемы |
F, Н |
H, м |
а, м |
b, м |
Номер двутавра |
10–3 , м/кН |
[], МПа |
| 0 |
0 |
450 |
0,18 |
4,0 |
2,2 |
16 |
30 |
150 |
| 1 |
1 |
500 |
0,17 |
3,6 |
2,0 |
18 |
29 |
155 |
| 2 |
2 |
550 |
0,16 |
3,2 |
1,9 |
20 |
28 |
160 |
| 3 |
3 |
600 |
0,15 |
2,8 |
1,8 |
20а |
27 |
165 |
| 4 |
4 |
650 |
0,19 |
2,4 |
1,6 |
22 |
26 |
170 |
| 5 |
5 |
700 |
0,10 |
2,0 |
1,7 |
22а |
25 |
175 |
| 6 |
6 |
750 |
0,11 |
3,8 |
2,6 |
24 |
24 |
180 |
| 7 |
7 |
800 |
0,12 |
3,6 |
2,4 |
24а |
23 |
185 |
| 8 |
8 |
850 |
0,09 |
3,4 |
2,8 |
18а |
22 |
190 |
| 9 |
9 |
900 |
0,08 |
3,2 |
2,3 |
27 |
21 |
195 |
| ххх |
в |
б |
а |
в |
в |
б |
а |
в |
При решении задачи необходимо учесть, что балка подвергается действию поперечного (изгибающего) удара. Для упрощения расчетов необходимо принять следующие допущения: 1) деформации конструкции от воздействия ударяющего тела подчиняются закону Гука и подобны деформациям, возникающим при статическом приложении той же нагрузки; 2) ударяющее тело является абсолютно жестким и с момента соприкосновения с конструкцией остается связанным с ней во время всего ее дальнейшего перемещения; 3) работа, совершаемая падающим телом, полностью преобразуется в энергию деформации конструкции.
Перемещение точки приложения груза F необходимо вычислить на основе способа Верещагина при статическом нагружении. После определения этого перемещения следует вычислить динамический коэффициент и наибольшее напряжение от статического приложения силы F, построив предварительно эпюры изгибающих моментов.
При выполнении п.3 настоящей задачи следует иметь в виду, что податливость пружины представляет собой ее осадку от груза весом 1 кН.