Методические указания по выполнению лабораторной работы для студентов очной и заочной формы обучения по дисциплине Метрология, стандартизация и сертификация Екатеринбург

СОДЕРЖАНИЕ: Стандартизация, метрология и сертификация являются инструментами обеспечения качества продукции, работ и услуг

Федеральное агентство по образованию

Уральский государственный политехнический университет

Кафедра метрологии стандартизации сертификации

Н.К. Казанцева

ОЦЕНКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Методические указания по выполнению лабораторной работы

для студентов очной и заочной формы обучения

по дисциплине – Метрология, стандартизация и сертификация

Екатеринбург

2005

Введение

Стандартизация, метрология и сертификация являются инструментами обеспечения качества продукции, работ и услуг.

Управление качеством невозможно представить без контроля над качеством, который базируется на учете многочисленных результатов измерений показателей качества.

В современной промышленности доля затрат труда на выполнение измерений в среднем составляет 10% общих трудозатрат на всех этапах жизненного цикла продукции, а в таких отраслях, как, например, химическая промышленность, электроника доля общих трудозатрат на измерения достигает даже 60%.

Измерения, методы и средства обеспечения их единства, а также способы достижения необходимой точности измерений изучает наука, называемая метрологией.

С помощью измерений получают информацию о состоянии производственных, экономических и социальных процессов.

Только достоверность и точность измерительной информации обеспечивают правильность принятия решений на всех уровнях рассмотрения вопроса о качестве продукции, при испытаниях изделий, в научных экспериментах и т.д.

Один из конкретных вопросов, касающийся этой проблемы – это оценка точности результатов измерений, полученных механическими измерительными приборами. Описанная ниже лабораторная работа предназначена для усвоения общих сведений по основам технических измерений и получения практических навыков в определении точности результатов измерений.

Лабораторная работа

«Оценка результатов измерений наружных цилиндрических поверхностей»

Цель работы: освоить закономерности выбора измерительных средств, научиться измерять действительные размеры и оценивать результаты измерений.

Общие сведения

Метрология - область знаний и вид деятельности, связанные с измерениями.

Измерение – совокупность операций по применению технического средства, хранящего единицу величины, обеспечивающих нахождение соответствия измеряемой величины с ее единицей в явном или неявном виде и получение значения этой величины.

В метрологии по существу измерение является процессом нахождения физической величины опытным путем с помощью средств измерительной техники.

Средство измерения - техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящие и хранящие единицу величины, размер которой принимается неизменным в пределах установленной погрешности в течение известного интервала времени.

Эталон единицы величины – средство измерений, предназначенное для воспроизведения и хранения единицы величины, кратных или дольных ее значений с целью передачи размера другим средствам измерений данной величины.

Единство измерений – состояние измерений, при котором их результаты выражены в узаконенных единицах величин, а погрешности измерений не выходят за установленные границы с заданной вероятностью.

Итак, первым условием обеспечения единства измерений является представление результатов измерений в узаконенных единицах, которые были бы одними и теми же всюду, где проводятся измерения и используются их результаты. В России – это величины единиц Международной системы единиц. Второе условие единства измерений - погрешность измерений не превышает (с заданной вероятностью) установленных пределов. Погрешности измерений средства измерений указываются в придаваемом к нему техническом документе – паспорте,

технических условиях или других документах.

Измерение физической величины производят путем ее сравнения в процессе эксперимента с величиной, принятой за единицу физической величины.

Классификация измерений приведена на рис. 1.

Измерения, связанные с различными видами получения информации,

бывают четырех типов: прямые, косвенные, совокупные, совместные.

Наиболее распространены прямые и косвенные

Прямым называют измерение, при котором значение физической величины получают путем непосредственного сравнения ее с мерой (взвешивание, измерение длины и т.д.).

Косвенным называют измерение, при котором результат определяют на основании прямых измерений величин, связанных с определяемой величиной известной зависимостью (определение сопротивления по закону Ома, если измерены сила тока и напряжение).

Совокупные измерения связаны с определением значения величины, являющейся результатом решения системы уравнений, составляемых по итогам одновременных измерений нескольких однородных величин.

Совместные измерения представляют собой измерения двух и более неоднородных физических величин для определения зависимости между ними.

При прямых измерениях используются следующие основные методы: метод непосредственной оценки, метод сравнения с мерой, дифференциальный метод, нулевой метод и метод совпадения.

При косвенных измерениях применяют преобразование измеряемой величины в процессе измерений. По отношению к основным единицам измерения виды измерений разделяют на контактный и бесконтактный.

Различия в характере динамики измеряемой величины обусловили существование трех разновидностей измерений.

Статические измерения проводятся при измерении практически постоянной величины.

Динамические измерения проводят при измерении величин, изменяющихся в процессе измерений.

Статистические измерения связаны с определением параметров случайных процессов (например, уровня шума).

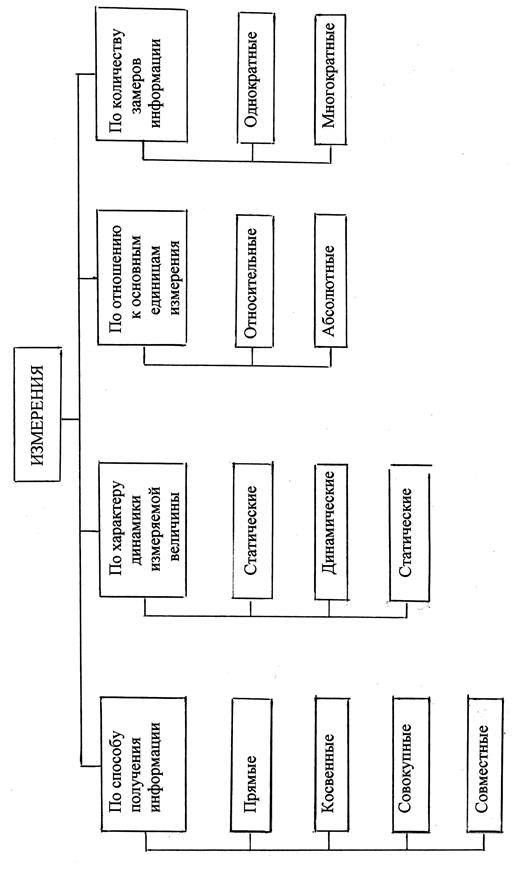
При абсолютных измерениях используют прямое измерение основной величины и физическую константу (например, скорость света, ускорение свободного падения и др.).

При относительных измерениях устанавливают отношение измеряемой величины к однородной, используемой в качестве единицы.

С точки зрения количества замеров величин различают однократные и многократные измерения.

Однократные измерения предполагают соответствие числа измерений числу измеряемых физических величин.

Многократные измерения предполагают большее число измерений, чем количество измеряемых величин.

Количественной характеристикой измеряемой величины служит ее размер. При анализе измерений следует четко разграничивать два понятия: истинные значения физических величин и их эмпирические проявления – результаты измерений.

Истинные значения физических величин – это значения, идеальным образом отражающие свойства данного объекта, как в количественном, так и в качественном отношении. Они не зависят от средств нашего познания и являются абсолютной истиной.

Результаты измерений, напротив, являются продуктами нашего познания. Представляют собой приближенные оценки значений величин, найденные путем измерения. Они зависят не только от истинных значений величин, но еще и от метода измерения, от технических средств, с помощью которых проводятся измерения, и от свойств органов чувств наблюдателя, осуществляющего измерения.

Погрешностью измерения называется разница между результатами измерения Х и истинным значением Q измеряемой величины:

= Х – Q (1)

Поскольку истинное значение Q измеряемой величины неизвестно, то неизвестны и погрешности измерения, поэтому для получения хотя бы приближенных сведений о них приходится в формулу (1) вместо истинного значения подставлять так называемое действительное значение.

Действительный размер – размер элемента установленный измерением. Значение физической величины, найденное экспериментальным путем и приближающееся к истинному значению настолько, что для данной цели может применяться вместо него, называется действительным.

Номинальный размер – основной размер, определяемый исходя из функционального назначения детали или узла. Он проставляется на чертеже и служит началом отсчета отклонений.

Два предельно допускаемых размера, между которыми должен находится действительный размер годной детали, называются предельными размерами.

Причинами возникновения погрешности являются:

- несовершенство методов измерений;

- несовершенство технических средств, применяемых при измерениях;

- ошибки органов чувств наблюдателя в процессе измерения;

- условия проведения измерений.

Указанные причины возникновения погрешностей определяются

совокупностью большого числа факторов, под влиянием которых складывается суммарная погрешность измерения.

При определении годности детали по размеру устанавливается

соответствие действительного размера с предельными размерами:

d max d r d min , (2)

где d r – действительный размер поверхности детали;

d max - наибольший предельный размер поверхности детали;

d min - наименьший предельный размер поверхности детали.

Порядок выполнения работы

1. Познакомиться с общими сведениями определения результатов

измерения и оценки годности детали.

2. По варианту задания получить у преподавателя эскиз детали и саму деталь. Уяснить, какие поверхности детали должны подвергаться измерению и оценке годности.

3. Заполнить все исходные данные в табл. 1.

Допуск размера определяется как разность между наибольшим

и наименьшим предельными размерами или как алгебраическая разность между верхним и нижним предельными отклонениями.

Таблица 1

Исходные данные для определения результатов измерений

Наименование детали и контролируемая поверхность	Величина допуска размера, мм	Номинальный размер,мм	Предельные размеры, мм
			d min	d max
Наружная цилиндрическая поверхность
Торцевая поверхность

4. По внешнему виду детали, номинальному размеру и величине

допуска выбрать измерительный инструмент, используя РД 50-98-86. У выбранного инструмента определить пределы измерения, цену деления, предельную погрешность измерения. Из предложенных в РД 50-98-86 универсальных измерительных средств для измерения наружных линейных размеров в лаборатории имеются штангенциркули и микрометры гладкие. Описание приборов дано в приложениях 1,2.

5. Провести настройку выбранных измерительных средств. Порядок и

правильность настройки уточнить по технической инструкции или по справочным данным (приложения 1,2).

6. Провести измерение действительных размеров (не менее 10

измерений каждой поверхности детали). Экспериментальные данные занести в табл. 2.

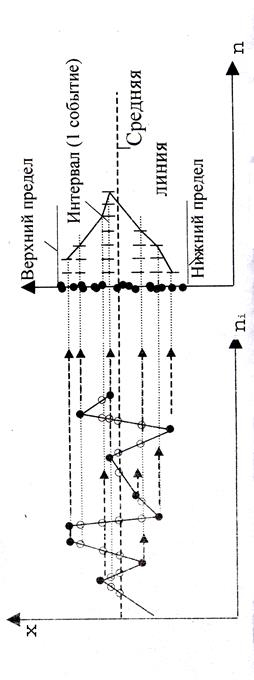
7. Представить полученные результаты измерений в виде графиков.

Зависимость действительных размеров от последовательности их получения и зависимость действительного размера от их количества одинаковых значений (рис.2). Найти среднеквадратичное отклонение

8. Оценить результат измерений. Оценить результат – значит

приписать ему погрешность с заданной доверительной вероятностью. При небольшом числе измерений п обычно используют распределение случайной величины, предложенное Стьюдентом. Вид распределения по этому закону зависит не только от значения случайной величины, но и от числа наблюдений п.

При п распределение Стьюдент совпадает с распределением по нормальному закону, а при п 20 оно резко отличается от нормального закона.

Таблица 2

Действительные размеры детали

Контролируемая поверхность

Схема измерений

Численные значения действитель-

ных размеров, мм

(10 измерений),

Среднее значение результатов измерений, мм

Наружная цилиндрическая

поверхность

Измерение диаметра

Х 1

Х 2

Х 3

…

Х 10

Торцевая поверхность

Измерение длины

У 1

У 2

У 3

…

У 10

Для оценки границ доверительного интервала погрешности

среднего значения воспользуемся распределение Стьюдента (прил. 3).

Сначала, используя данные табл.2, определим значение разности между действительным и средним размерами для каждого измерения:

V i = X i - X (3)

Полученные значения занесем в табл. 3.

Далее следует найти среднеквадратичное отклонение S :

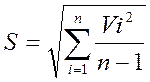(4)

Таблица 3

Нахождение среднеквадратичного отклонения

№ Измере

ния

Разность

V, mm

8. Оценить результат измерений.

Оценить результат измерений – значит приписать ему погрешность с

заданной доверительной вероятностью. При небольшом числе измерений п обычно используют распределение случайной величины, предложенное Стьюдентом. Вид распределения по этому закону зависит не только от значения случайной величины, но и от числа наблюдений п.

При выполнении лабораторной работы необходимо установить доверительные границы случайной погрешности для следующих случаев:

при заданной доверительной вероятности р = 0,95 и при количестве измерений п = 5 и п = 10:

при р = 0,98 и при п = 5 и п = 10.

e = t ( p ) S (5)

Таблица интеграла распределения Стьюдента t ( p ) дана в прил. 3.

9. Далее необходимо записать средний действительный размер

детали для каждой поверхности с указанием доверительных интервалов всех четырех вариантов и проанализировать влияние количества измерения и величину доверительной вероятности на величину доверительного интервала.

10. Сделать заключение о соответствии или несоответствии

полученного действительного размера и заданного предельного размера.

11. На основе приведенной классификации (рис.1) определить все

использованные приемы измерения по способу получения информации, по

характеру динамики измеряемой величины, по отношению к основным единицам измерения, по количеству замеров информации.

12. Составить отчет о проделанной работе.

Требования к отчету

По выполненной работе оформляется индивидуальный отчет, в котором необходимо предоставить:

- название и конкретную цель работы;

- эскиз измеряемой детали;

- сведения о размерах и допусках детали (табл.1);

- правила выбора измерительного средства;

- метрологические характеристики выбранных измерительных средств, а именно: пределы измерений, цена деления, погрешность;

- результаты измерений (табл.2);

- графики распределения полученных результатов в соответствии с рис.2;

- оценку результатов измерений при доверительной вероятности

р = 0,95 и 0,98. Указать среднеквадратичное отклонение S, отклонение

разности V

- указать доверительные интервалы измерений e ;

- представить анализ точности измерения наружного цилиндрического

размера в зависимости от количества измерений и величины доверительной вероятности;

- выводы, сделанные исходя из цели работы, в которых дать заключение о соответствии или несоответствии заданного размера детали и действительного размера с учетом доверительного интервала.

Оборудование рабочего места

Техническое оснащение рабочего места для выполнения лабораторной работы включает:

- измеряемую деталь (группу деталей) с наружной цилиндрической поверхностью и плоскими торцевыми поверхностями;

- эскиз детали;

- измерительные средства: штангенциркуль, гладкий микрометр;

- концевые плоскопараллельные меры длины (при необходимости настройки измерительных средств на величину отличную от нуля).

При выполнении работы следует использовать следующую нормативно-техническую документацию:

- РД 50-98-86, Методические указания. Выбор универсальных средств измерений линейных размеров до 500 мм;

- ГОСТ 6507-78. Микрометры с ценой деления 0,01 мм. Технические условия;

- ГОСТ 166-89 Штангенциркули. Технические условия.

Приложение 1

Универсальные измерительные средства

1. Штангенинструменты

Штангенинструмент – группа измерительных средств для измерения

и разметки линейных размеров методом непосредственной оценки. Отсчетное устройство штангенинструмента состоит из измерительной линейки штанги с делениями через 1 мм и вспомогательной подвижной шкалы нониуса для отсчета частей делений основной шкалы, нанесенной на штанге.

В основу отсчета по нониусу положена способность человеческого глаза оценивать совпадение и несовпадение штрихов двух сомкнутых шкал более точно при определении долей деления по одной шкале.

Нониусная шкала (рис. 3) имеет небольшое число интервалов деления 10-20 по сравнению с основной шкалой. Нулевой штрих нониуса является указателем числа целых делений основной шкалы. Отсчет по нониусу сводится к определению совпадения одного из штрихов нониуса с соответствующим штрихом основной шкалы.

Модуль нониуса является мерой «растяжки» шкалы и показывает, сколь делений основной шкалы соответствует одному делению шкалы нониуса. Модуль принимается равным 1; 2: и 5, а отсчеты по нониусу – 0,1; 0,05 и 0,02 мм. Отсчет по нониусу 0,02 мм практически не применяется, т.к. погрешность отсчета не менее, чем погрешность при отсчете 0,05 мм.

К штангенинструментам относятся штангенциркули, штангенглубиномеры, штангенрейсмасы и штангензубомеры. Эти инструменты имеют общую конструкцию – штангу с основной шкалой и подвижную рамку с нониусом.

Общий вид штангенциркуля показан на рис. 4.

Наибольшее распространение получили штангенциркули с диапазоном измерения от 0 до 140 мм или от 0 до 320 мм с отсчетом по нониусу 0,1 и 0,05 мм.

Измерение штангенциркулем наружного диаметра выполняют в следующей последовательности. Изделие помещают между губками, прижимают неподвижную губку к поверхности детали, перемещают подвижную губку до плотного контакта измерительной поверхности губки с поверхностью измеряемой детали. Закрепляют стопорный винт губки, снимают штангенциркуль с изделия и производят отсчет по основной шкале и нониусу.

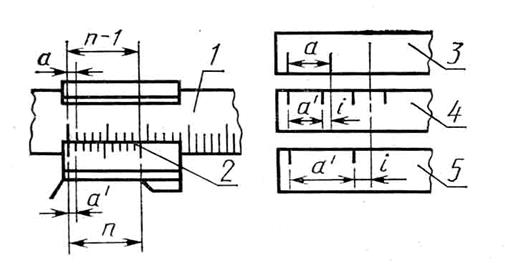
Рис. 3. Принцип построения нониуса.

1 - основная шкала; 2 - шкала нониуса; 3,4,5 - нониус

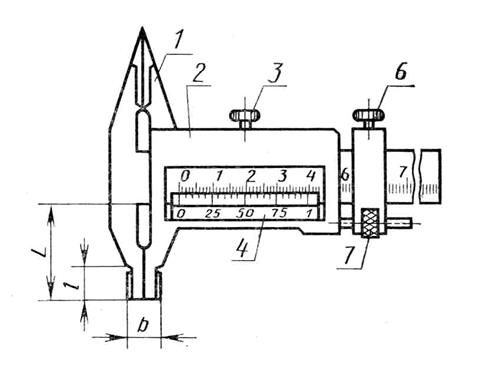
Рис. 4. Общий вид штангенциркуля.

1 - измерительные губки; 2 - подвижная рамка;

3 - стопорный винт на подвижной рамке; 4 – нониус; 5 - винт

на штанге;

6 - микрометрическая подача для медленного перемещения рамки по

штанге.

Приложение 2

Микрометрические инструменты

Микрометрические инструменты служат для наружных измерений, внутренних измерений, глубины пазов, отверстий и длин уступов. Общим узлом для всех микрометрических инструментов является микрометрическая головка.

Известно, что при неподвижной гайке один оборот винта соответствует его осевому перемещению, равному шагу резьбовой пары винт-гайка. Для отсчета дольных значений в микрометрическую головку введена дополнительная шкала.

Для наружных измерений используют микрометр гладкий (рис. 5).

Наибольшее применение имеют микрометры с диапазоном измерения до 600 мм.

Для установки на нуль микрометров с диапазоном измерения свыше 25 мм (больше длины резьбы винта) применяются установочные меры в виде цилиндра, у которого размер между торцевыми поверхностями равен нижнему пределу измерения микрометра. Микрометры можно настраивать на нуль или любой другой размер (например, номинальный) по концевым мерам длины, в результате чего точность отсчета повышается по сравнению с обычным использованием микрометра.

Перед измерением микрометр устанавливают на нуль. Для этого, вращая микровинт за трещотку, плавно подводят его торец к торцу пятки установочной меры до момента плотного контакта измерительных пяток, когда трещотка начнет провертываться. В этом положении нулевой штрих шкалы барабана должен совпадать с нулевым штрихом стебля. Закрепляют стопор микровинта, разъединяют барабан и микровинт, отвертывают трещотку. Совмещают нулевой штрих барабана с продольным штрихом стебля и после этого вращают по часовой стрелке корпус трещотки до плотного закрепления барабана на микровинте. Освобождают стопор микровинта. При измерении детали плавно вращают трещотку до момента начала ее привертывания. Стопорят микровинт и определяют размер детали, который равен сумме показаний, снятых с продольной шкалы стебля (в мм) и круговой шкалы барабана (сотых долей мм).

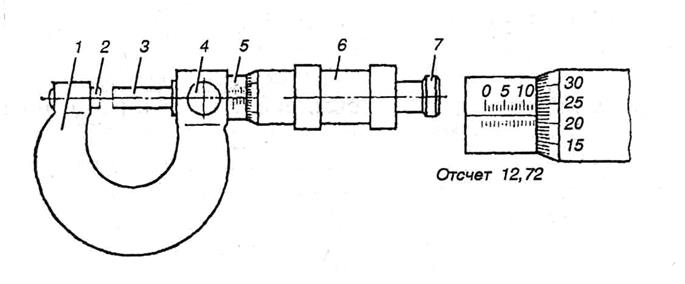
Рис. 5. Общий вид микрометра гладкого

1 – скоба; 2 – неподвижная измерительная пятка;

3 - микрометрическая головка с подвижной измерительной пяткой;

4 - стопор микровинта; 5 - стебель микрометрической головки;

6- барабан микрометрической головки; 7 -трещотка

Приложение 3

Таблица интеграла распределение Стьюдента

п	Значение t от доверительной вероятности и числа измерений
п	Р=0,80	Р=0,90	Р=0,95	Р=0,98	Р=0,99
2	3,080	6,31	12,71	31,80	63.70
3	1,886	2,92	4,30	6,96	9,92
4	1,638	2,35	3,18	4,54	5,84
5	1,533	2,13	2,77	3,75	4,60
6	1,476	2,02	2,57	3,36	4,03
7	1,440	1,943	2,45	3,14	3,71
8	1,415	1,895	2,36	3,00	3,50
9	1,397	1,860	2,31	2,90	3,36
10	1,383	1,833	2,26	2,82	3,25
11	1,372	1,812	2,23	2,76	3,17
12	1,363	1,796	2,20	2,72	3,11
13	1,356	1,782	2,18	2,68	3,06
14	1,350	1,771	2,16	2,65	3,01
15	1,345	1,761	2,15	2,62	2,98
16	1,341	1,753	2,13	2,60	2,95
17	1,337	1,746	2,12	2,58	2,92
18	1,333	1,740	2,11	2,57	2,90
19	1,330	1,734	2,10	2,55	2,88
20	1,328	1,729	2,09	2,54	2,86
1,282	1,645	1,96	2,33	2.58

Скачать архив с текстом документа