Методические указания Под редакцией проф. А. М. Большакова

СОДЕРЖАНИЕ: М лабораторные работы по физической химии: Методические указания /Сост.: А. И. Мишустин, К. Ф. Белоусова. Под ред. А. М. Большакова. Федер агентство по образованию, Моск гос ун-т инж экологии, ф-т экологии и природопользования, каф. «Общая и физическая химия». — М.: Мгуиэ, 2009. — с

ЛАБОРАТОРНЫЕ РАБОТЫ

ПО ФИЗИЧЕСКОЙ ХИМИИ

2009

Издательский центр

МГУИЭ

Федеральное агентство по образованию

Федеральное агентство по образованию

Московский государственный университет

инженерной экологии

Факультет экологии и природопользования

Кафедра «Общая и физическая химия»

ЛАБОРАТОРНЫЕ РАБОТЫ

ПО ФИЗИЧЕСКОЙ ХИМИИ

Методические указания

Под редакцией проф. А.М.Большакова

Составители:

А.И.Мишустин,

к.ф. бЕЛОУСОВА

Москва

МГУИЭ

200 9

Учебное издание

Составители:

Мишустин Александр Иванович,

Белоусова Кира Филипповна

Лабораторные работы

по физической химии

под редакцией проф. А.М.Большакова

Редактор В.И. Лузева

Формат бум. 60 x 84 1/16.

Объем усл. п. л. . Уч.-изд. л. . Тираж экз. Зак.

МГУИЭ, издательский центр,

105066 Москва, Старая Басманная ул., 21/4

УДК 541.1

ББК

Рецензенты: кафедра

канд. хим. наук

Допущено редакционно-издательским советом МГУИЭ

Мишустин А.И., Белоусова К.Ф.

М Лабораторные работы по физической химии: Методические указания /Сост.: А.И. Мишустин, К.Ф. Белоусова. Под ред. А.М. Большакова. Федер. агентство по образованию, Моск. гос. ун-т инж. экологии, ф-т экологии и природопользования, каф. «Общая и физическая химия». — М.: МГУИЭ, 2009. — с.

Методические указания предназначены студентам, обучающимся
по всем специальностям МГУЭИ, при изучении дисциплины
«Физическая химия».

УДК 541.1

ББК

составление 2009

Лабораторная работа 1.

Кинетика каталитической реакции

разложения перекиси водорода

Цель работы

Нахождение кинетического уравнения для каталитической реакции разложения перекиси водорода с определением численных значений порядка реакции и константы скорости реакции при температуре опыта.
Определение зависимости константы скорости исследуемой реакции от температуры с нахождением констант в уравнении Аррениуса – предэкспоненциального множителя и энергии активации.

Теоретическое введение

Химическая кинетика изучает скорость и механизм химических реакций.

Скорость химической реакции( w) в гомогенной системе, имеющей постоянный объем, измеряется изменением концентрации вещества (C), прореагировавшего в единицу времени (t)

w = ± dC/dt.

d – знак дифференциала, то есть бесконечно малого изменения величины.

Скорость всегда положительная величина, поэтому в приведенной формуле выбирают соответствующий знак: плюс, если скорость выражают через концентрацию конечного продукта реакции и минус, если скорость выражают через концентрацию начального продукта, так как со временем начальные продукты расходуются, а конечные накапливаются.

Скорость химической реакции можно выразить изменением молярной концентрации любого из участников реакции в единицу времени, (например, в секунду). Единицы измерения скорости реакции в этом случае – моль/(л·с).

Будем рассматривать реакции, которые идут практически до конца, - односторонние реакции .

Пусть количества реагирующих веществ связаны между собой уравнением реакции:

aA + bB ® lL + mM,

где a, b, l, m – стехиометрические коэффициенты.

Соотношения между скоростью реакции по разным компонентам можно выразить следующим образом:

±dC/dt = 1/a(-dC_A /dt) =1/b(-dC_B /dt) =1/l· dC_L /dt =1/m·dC_M /dt,

Скорость реакции тем больше, чем больше концентрации веществ, вступающих в реакцию, так как при большем числе реагирующих частиц в единице объема и при большом числе столкновений между ними в единицу времени увеличивается вероятность их химических превращений. Однако между скоростью и концентрацией нет прямой зависимости, поэтому уравнение химической реакции отражает материальный баланс процесса и, в общем случае, не отражает истинного механизма реакции.

Основной постулат химической кинетики – кинетический закон действующих масс (ЗДМ): - при постоянной температуре скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ, каждая из которых возведена в степень, называемую порядком реакции по данному веществу. Для приведенной выше реакции ЗДМ имеет вид:

w = ± dC/dt = kC_A ⁿ ^A C_B ⁿ ^B ,

где k – коэффициент пропорциональности, называемый константой скорости реакции ; n_А , n_В – порядок реакции по компонентам А и В соответственно. Общий порядок реакции n = n_A + n_B . Порядок – безразмерная величина, которая, как правило, может принимать как целые (0,1,2,3), так и дробные значения.

В общем случае порядок по компоненту не совпадает с соответствующим стехиометрическим коэффициентом в уравнении реакции. Совпадение возможно только для простых (одностадийных) процессов, например для реакции : H₂ + I₂ = 2HI -dC_H ₂ /dt = -dC_I ₂ /dt = k·C_H ₂ ·C₂ , где n_H ₂ = n_I ₂ = 1, n = 1+1=2.

Константу скорости реакции называют удельной скоростью, она численно совпадает со скоростью реакции в момент времени, когда концентрации всех реагирующих веществ равны единице. Единицы измерения константы скорости реакции – [(л/моль)^{n - 1} (с)^-1 ].

Выведем кинетическое уравнение для реакции n-порядка, представленной следующим уравнением

A + B +··® L

Допустим, что C_A = C_B = ... = C, исходные концентрации этих веществ также одинаковы и каждая из них равна C₀ .

Тогда w = -dC/dt = kCⁿ

Поле интегрирования и нахождения константы интегрирования (при t = 0, C = C₀ ) получаем кинетическое уравнение для реакции n-порядка

kt = [1/( n – 1)] · {[1/ C⁽ ^{n – 1)} ] – [1/ C₀ ⁽ ^{n – 1)} ] }

Важной кинетической характеристикой реакции является время полупревращения( период полураспада) - t – время, за которое начальная концентрация исходного вещества уменьшается в два раза, C = 1/2C₀ .

Для определения порядка реакции используют следующие методы

1. Метод подстановки.

2. Графический метод.

3. Универсальный метод.

4. Метод, основанный на определении определенной доли превращения исходного вещества.

5. Метод избытков Оствальда,

Большинство методов требует построения графической зависимости изменения концентрации реагирующего вещества от времени.

В данной лабораторной работе студентам предлагается использовать метод определения порядка реакции по времени превращения определенной доли исходного вещества. Подробно этот метод рассмотрен в описании расчетной части работы.

Зависимость скорости реакции от температуры

При повышении температуры скорость реакции растет. Фактически увеличивается константа скорости реакции.

Ориентировочно зависимость константы скорости реакции от температуры оценивают правилом Вант-Гоффа, согласно которому повышение температуры (T) на каждые 10⁰ приводит к увеличению константы скорости реакции (k) в 2 – 4 раза:

g = k_T _{+ 10} /k_T ,

где g - температурный коэффициент Вант-Гоффа.

Это правило справедливо в узком температурном интервале и при невысоких температурах.

Более точно зависимость константы скорости от температуры передает уравнение Аррениуса: k = k₀ exp(-E/RT) или k = k₀ e^(- ^E/ ^RT) - экспоненциальная форма уравнения, lnk = A - B/T -логарифмическая форма уравнения, где А = lnk₀ , B = E/R.

A, B – эмпирические константы, характерные для данной реакции.

Е – энергия активации, единицы измерения – [Дж/моль].

k ₀ – предэскпоненциальный множитель . R – универсальная газовая постоянная ([Дж/(моль·К)], Т– абсолютная температура, [K]. Физический смысл k₀ – константа скорости реакции при бесконечно высокой температуре.

Чтобы понять причину температурной зависимости скорости химической реакции нужно вспомнить, что для осуществления химического превращения обязательным условием является столкновение реагирующих частиц. Однако не любое столкновение приводит к химическому превращению.

Если бы при каждом соударении происходила реакция, то скорость её была бы на 10 – 20 порядков выше, чем в действительности. Следовательно, не все соударения приводят к реакции, а только такие, при которых между реагирующими частицами преодолеваются силы отталкивания, рвутся старые химические связи и возникают новые . (Дополнительным условием является благоприятная геометрическая ориентация реагирующих частиц друг относительно друг друга, ее учитывает так называемый стерический фактор). Такие соударения называются активными. Говорят, что в этом случае сталкивающиеся молекулы преодолевают энергетический барьер, величину которого называют энергией активации. Молекулы, способные преодолеть этот барьер, называют активными. Они обладают энергией, равной или большей, чем энергия активации процесса. Энергия активации является свойством процесса.

Основной причиной температурной зависимости химической реакции с ростом температуры является не увеличение скорости движения молекул, а увеличение числа активных молекул, и, соответственно числа активных соударений в единицу времени.

Влияние катализатора на скорость химической реакции

Катализом называется явление изменения скорости реакции под действием некоторых веществ - катализаторов, которые, участвуя в реакции, не входят в состав конечных продуктов.

Положительные катализаторы увеличивают скорость химической реакции. Это самый дешевый способ ускорить процесс. Отрицательные катализаторы замедляют ее скорость, такие катализаторы называют ингибиторами.

По фазовому признаку различают гомогенный и гетерогенный катализ. При гомогенном катализе катализатор и продукты реакции находятся в одной фазе, при гетерогенном – в разных фазах.

Катализатор изменяет механизм реакции на более выгодный энергетически. Например, для реакции N₂ + 3H₂ = 2NH₃

в отсутствии катализатора Е @ 300 кДж/моль, ,

в присутствии катализатора Е = 163 кДж/моль.

Катализатор (К), принимая участие в реакции, образует с реагентами промежуточные соединения, а затем высвобождается.

Так, уравнение реакции А + В = АВ не отражает реальный механизм процесса в присутствии катализатора. Такой процесс фактически протекает по стадиям: - А + К = АК, АК + В = АВ + К.

Катализ относится к сложным реакциям, т.е. протекающим в несколько стадий.

Самая медленная (лимитирующая ) стадия определяет скорость всего процесса.

Экспериментальная часть

В работе изучают реакцию разложения перекиси водорода 2Н₂ О₂ 2Н₂ О + О₂

в присутствии катализатора – водного раствора бихромата калия (K₂ Cr₂ O_7. ). Каталитическим действием обладают ионы Cr₂ O₇ ^2- .

Действие катализатора может быть прослежено по изменению окраски реакционного раствора, так как исходные и промежуточные продукты окрашены различно. При завершении процесса разложения перекиси водорода первоначальная окраска раствора катализатора полностью восстанавливается, кроме того, прекращается выделение пузырьков кислорода.

Реакция протекает в 2 стадии:

2H₂ O₂ + Cr₂ O₇ ^2- Cr₂ O₉ ^2- + 2H₂ O желто-оранж. зелено-оранж.

2. Cr₂ O₉ ^2- O₂ + Cr₂ O₇ ^2- зелено-оранж. желто-оранж

Исследование кинетики реакции проводится с помощью измерения давления выделяющегося кислорода U-образным манометром. Манометр заполнен окрашенным водным раствором. Реакционный сосуд, содержащий смесь растворов перекиси водорода и катализатора, соединяется с манометром.

Опыт проводят при комнатной температуре при постоянном объеме в системе, отсоединенной от окружающей среды. Регистрируется время и высоты уровней жидкости в левом и правом колене манометра (l₁ и l₂ ). Разность высот уровней равно давлению (в мм водного столба). По изменению давления судят о количестве разложившейся перекиси водорода. Результаты опыта записывают в таблицу 1.

Заранее число измерений неизвестно, поэтому для таблицы следует отвести целую страницу тетради.

Перед началом опыта в таблице 1 указывают:

1. Исходное положение уровней жидкости в коленах манометра.

2. Два первоначальных значения уровня жидкости по одному из колен манометра, например, по левому (l₂₁ ,l₂₃ ), отстоящие от начального (l₂₀ ) до ближайшего целого числа (в пределах 10мм) и последующего (l₂₁ ) на 10 мм.

3. 5-6 значений высоты уровня жидкости (l₂₄ , l₂₅ ,l₂₆ ,l₂₇ l₂₈ ,), отстоящие от предыдущего значения (l₂₃ ) и друг от друга на 5 мм.

В дальнейшем экспериментальные данные (t_i , l₁ _i , l₂ _i ) вносят в таблицу при изменении уровня жидкости в выбранном колене (l₂ )манометра на 5мм.

Эксперимент проводит бригада, состоящая из трех студентов. Каждый член бригады записывает в таблицу значение одной из характеристик процесса: t_i , l₁ _i , l₂ _i .

Недопустимо фиксировать уровень жидкости только в одном колене манометра, а второе рассчитывать, так как внутренний диаметр трубок манометра не стандартизирован, и полученный результат можетсодержать ошибку.

Таблица 1.

Время от начала опыта, _ti			Уровни жидкости в коленах манометра l		Давление выделившегося кислорода, P_i = l₁ _i – l₂ _i , мм	Концентрация Н₂ О₂ , С_i , моль/л
мин-с ₌		с	левое l₁ _i , мм	правое l₂ _i , мм		Концентрация Н₂ О₂ , С_i , моль/л
(l₁₀ )	(l₂₀ )	Р₀ =0	С₀ = 0,22
			(l₁ ₁ )	(l₂₁ )	(P₁ )	(C₁ )
(l₁ ₂ )	(l₂₂ )	(P₂ )	(C₂ )
(l₁ ₃ )	(l₂₃ )	…	…
…	…	…	…
…	…	…	…
(l₁ _i )	(l₂ _i )	…	(C_i )
…	…	…	…
…	…	…	…
t_n	(l_1n )	(l_2n )	(P_n )	(C_n )
После полного разложе-ния Н₂ О₂ и приведе-ния к температу-ре опыта			l₁ =	l₂ =	Р = l₁ - l₂ =	0

Порядок проведения эксперимента

В реакционный сосуд через воронку выливают 1-3 мл раствора катализатора, полученного у преподавателя, и 10 мл рабочего раствора перекиси водорода, отмеренного с помощью мерной пробирки. Реакционный сосуд быстро соединяют резиновым шлангом с манометром и оставляют в стакане с водой комнатной температуры.

Колено манометра, соединенное с реакционным сосудом, c помощью крана отсоединяют от атмосферы. Этот момент считают началом опыта. Включают секундомер. Опытные данные вносят в таблицу.

Приблизительно через 30 мин. от начала опыта увеличение давления станет медленным (2 мм водного столба/мин). Тогда записывают последнее показание секундомера (t_n ) и значениz уровней жидкости в коленах манометра (l₁ _n , l₂ _n ).

Далее сосуд с реакционной смесью помещают в стакан с горячей водой и выдерживают там до тех пор, пока не прекратится выделение пузырьков кислорода и не восстановится первоначальный цвет раствора (10 мин.).

После этого возвращают реакционный сосуд в стакан с водой комнатной температуры до достижения постоянного значения давления в манометре (10 мин.) и записывают последние показания уровней жидкости в коленах манометра (l₁ , l₂ ). Рассчитывают установившееся давление (Р ).

В конце эксперимента все данные, полученные бригадой, сводят в одну таблицу. Такая таблица должна быть в тетради для лабораторных работ у каждого члена бригады. Записи делают ручкой.

Записывают температуру опыта и значение коэффициента Вант-Гоффа, сообщенное преподавателем.

Таблицу 1 с опытными данными подписывает преподаватель в день выполнения эксперимента. Внесение последующих исправлений в таблицу недопустимо .

Расчетная часть

В расчетах следует учесть рекомендации по округлению чисел, приведенные в конце описания лабораторной работы 2.

В таблицу 1 вносят рассчитанные по формуле величины P_i =l₁ _i -l₂ _i - значения давления выделившегося кислорода в данные моменты времени (t_i ).

Величины P_i и (P - P_i ) пропорциональны количествам соответственно разложившейся и неразложившейся перекиси водорода. Значение P пропорционально всему количеству взятого реагента и исходной его концентрации С₀ .

Величину С₀ /P можно считать коэффициентом пропорциональности для расчета текущей концентрации перекиси водорода:

C_i = (P - P_i )C₀ / P .

Найденные значения C_i вносят в таблицу 1.

Построение графика.

В координатах C-t на миллиметровой бумаге, формата А4, строят график зависимости текущей концентрации С_i (моль/л) от времени t_i (с) по данным таблицы 1.

Масштабы на осях координат размечают двумя-тремя зарубками, длина отрезков между зарубками должна быть кратна 10 (или степеням 10). Масштабы осей подбираются так, чтобы график занимал большую часть площади рисунка. У концов осей записывают откладываемую величину и в скобках её размерность. В точке пересечения осей графика должны быть нулевые значения.

Рис. 1. Зависимость концентрации перекиси водорода от времени.

После того, как оси размечены, откладывают экспериментально полученные точки в виде кружочков, (квадратиков, крестиков и других фигурок); иногда диаметр этих фигурок отражает точность измерений. Далее эти фигурки соединяют плавной линией, без изломов. Допустимо, что некоторые экспериментальные точки выпадают из линии за счёт случайных ошибок измерений.

Пример графика приведён на рисунке 1. Необходимо отметить, что в верхней части этого графика первые точки отражают переходные процессы, и делать описанные далее построения следует после окончания переходных процессов (указано стрелкой). Рисовать график следует карандашом.

Определение порядка и константы скорости реакции

С помощью графика 1 рассчитывают порядок реакции n и константу скорости k реакции в кинетическом уравнении

-dC/dt = k Cⁿ .

Сначала находят порядок реакции n , используя метод, который называется «метод нахождения порядка реакции по определенной доли превращения исходного вещества». Доля превращения исходного вещества в принципе может быть любой. В данной работе предлагается в расчетах взять долю превращения, равную 1/3. Методика расчетов сводится к следующему.

В средней наиболее информативной части графика 1 наметить три значения текущей концентрации перекиси водорода: С₀₁ , С₀₂ , С₀₃ . Удобно для расчетов, если эти значения будут представлять собой числа, кратные трем, например,

С₀₁ = 0,18, С₀₂ = 0,15, С₀₃ = 0,09.

Рассчитать значения концентраций С_1, С₂ , С₃ : С₁ = 2/3С₀₁ , С₂ =2/3С₀₂ , С₃ = 2/3С₀₃ .
С помощью графика 1 найти моменты времени t₀₁ , t₀₂ , t_03, соответствующие выбранным значениям концентраций С₀₁ , С₀₂ , С₀₃ , затем определить моменты времени t₁ , t₂ , t₃ , соответствующие концентрациям С_1, С₂ , С₃ .
Найти интервалы времени Dt₁ , Dt₂ , Dt₃ , за которые текущая концентрация c₀ _i уменьшилась на 1/3: Dt₁ = t₁ - t₀₁ , Dt₂ = t₂ - t₀₂ , Dt₃ = t₃ - t_03.
Найденные значения С₀ _i , С_i , Dt_i подставить в уравнения, полученные из преобразованного кинетического уравнения для реакции n–го порядка: (n₁ – 1) = [lg(Dt₁ /Dt₂ )] /[lg(С₀₂ /С₀₁ )], (n₂ – 1) = [lg(Dt₁ /Dt₃ )] /[lgС₀₃ /С₀₁ )], (n₃ – 1) = [lg(Dt₃ /Dt₂ )] /[lg(С₀₂ /С₀₃ )]. Из этих уравнений найти значения порядка реакции n_1, n₂ , n₃ , которые затем усреднить:

n = (n₁ + n₂ + n₃ )/3.

С усредненным значением порядка реакции n рассчитать константы скорости реакции k₁ , k₂ , k₃ для трех интервалов времени Dt₁ , Dt₂ , Dt₃ с помощью уравнений: k₁ Dt₁ = [1/(n – 1)] [1/С₁ ⁽ ⁿ ^{– 1)} – 1/С₀₁ ⁽ ⁿ ^{– 1)} ],

k₂ Dt₂ = [1/(n – 1)] [1/С₂ ⁽ ⁿ ^{– 1)} – 1/С₀₂ ⁽ ⁿ ^{– 1)} ],

k₃ Dt₃ = [1/(n – 1)] [1/С₃ ⁽ ⁿ ^{– 1)} – 1/С₀₃ ⁽ ⁿ ^{– 1)} ].

Найденные значения k₁ , k₂ , k₃ усреднить, определив, таким образом, константу скорости реакции:

k = (k₁ + k₂ + k₃ )/3.

7. Определить размерность константы скорости реакции по формуле: [k] = [(л/моль)ⁿ ^-1 ·с^-1 ].

Записать кинетическое уравнение для изученной реакции с найденными константами n и k.

Расчет предэспоненциального множителя и энергии активации в уравнении Аррениуса

k = k₀ e^- ^E ^/ ^RT

Предэкспоненциальный множитель (k₀ ) и энергия активации (Е ) – константы, не зависящие от температуры. Их можно рассчитать, если известно значение коэффициента Вант-Гоффа () для исследуемой реакции: = k_T ₊₁₀ /k_T ,

где k_T ₊₁₀ и k_T – константы скорости реакции при температурах (Т+10) и Т соответственно.

Используя значение температуры опыта (T), рассчитанную ранее величину константы скорости реакции (k ) и , заполнить таблицу 2.

Таблица 2.

Температура, Т (К)	Константа скорости реакции, k [(л/моль)ⁿ ^-1 ]·c^-1	1/T	lgk
Т (опыта)=	k_T =k =
Т = Т+10=	k = k_T+10 =
Т = Т+20=	k = k_T+20 =
Т = Т+30=	k = k_T+30 =

Примечания:

Температура должна быть выражена в градусах Кельвина.
Вместо десятичного, можно рассчитать значение натурального логарифма константы скорости. В этом случае в последующих расчетах не использовать коэффициент пересчета от натуральных к десятичным логарифмам (2,3).

Величины k₀ и E надо найти двумя методами – графическим и аналитическим. Указать размерность этих констант.

Аналитический метод

Для нахождения величины энергии активации использовать выражение, полученное после логарифмирования и алгебраического преобразования уравнения Аррениуса с применением данных таблицы 2.

Найти три значения энергии активации Е₁ , Е₂ , Е₃ , например, по следующим формулам: (E₁ /2,3/R) = (lgk – lgk )/(1/T - 1/T), (E₂ //2,3/R) = (lgk – lgk )/(1/T - 1/T), (E₃ //2,3/R) = (lgk - lgk )/(1/T - 1/T ).

Значение R следует брать равным 8,3 Дж/(моль·К). Размерность рассчитанного значения энергии активации – Дж/моль.

Усреднить найденные значения: Е_ан _. = 1/3(Е₁ + Е₂ + Е₃ ).

Величину предэкспоненциального множителя k_0ан. найти из уравнения Аррениуса при использовании полученного значения Е_ан. и данных любой строчки таблицы 2: k_0ан. = k·e^E ^/ ^RT .

Размерность k₀ совпадает с размерностью величины k _.

Графический метод

Если прологарифмировать уравнение Аррениуса, получится уравнение прямолинейной зависимости логарифма константы скорости (lnk) от обратной температуры (1/Т): lnk = lnk₀ - E/RT или с десятичными логарифмами: lgk = lgk₀ - E/2,3RT.

По данным таблицы 2 на миллиметровой бумаге (формат А5-А4) построить график в координатах lgk – 1/T. Пример построения графика приведен на рисунке 2.

Рис.2. Зависимость lgk от 1/Т

Масштаб желательно выбрать таким, чтобы график представлял собой прямую линию, с наклоном, близким к 45⁰ , так как при этом обеспечивается наибольшая точность графических определений. Экспериментальные точки лежат близко друг к другу, и через них надо очень тщательно провести прямую и продолжить до пересечения с вертикальной осью (дальняя экстраполяция). Отрезок, отсекаемый на оси ординат (при х = 1/Т = 0) равен lgk₀ . Найдя lgk₀ , определить величину и размерность k _{0 гр.}

Тангенс угла наклона графика 2 к оси х (1/Т) пропорционален величине Егр. :

(E _гр ./2,3/R) = (lgk - lgk)/(1/T - 1/T) = a/b = tg.

Величины катетов (lgk - lgk) = а, (1/T - 1/T) = b определить по графику 2 с учетом масштаба осей. Следует отметить, что тангенс угла наклона можно определить из любых двух точек графика 2. Напомним, что катеты должны быть выражена в единицах тех величин, которые отложены на осях графика, а не в единицах длины.

В заключение второй части расчетов следует написать уравнение Аррениуса с найденными (аналитическим или графическим методом) числовыми значениями констант.

Для защиты работы необходимо знать:

- Что такое скорость реакции? От каких факторов зависит скорость реакции?

- Основной постулат химической кинетики.

- Физический смысл константы скорости реакции. От чего зависит константа скорости реакции?

- Как связаны между собой порядок и молекулярность реакции?

- Физический смысл энергии активации и предэкспоненциального множителя.

- Исследуемая реакция простая или сложная? Ответ обосновать.

- Методы определения порядка реакций.

- Понятие о катализе.

ЛАБОРАТОРНАЯ РАБОТА 2.

ОПРЕДЕЛЕНИЕ СТЕПЕНИ ДИССОЦИАЦИИ И КОНСТАНТЫ ДИССОЦИАЦИИ СЛАБОЙ КИСЛОТЫ КОНДУКТОМЕТРИЧЕСКИМ МЕТОДОМ

Цель работы:

Ознакомление со способами выражения электропроводности электролитов и с экспериментальными методами ее определения. Экспериментальная проверка применимости закона действия масс к химическому равновесию реакции электролитической диссоциации слабого электролита в водном растворе. Экспериментальная проверка закона разбавления Оствальда.

Теоретическое введение

Закон действия масс характеризует состояние химического равновесия. Для обратимой химической реакции вида АВ А + В закон действия масс состоит в следующем: если в системе взаимодействующих веществ АВ, А и В установилось состояние химического равновесия, то отношение

K_c = C_A C_B /C_AB (1)

есть величина постоянная, зависящая только от температуры. Здесь К_с - константа равновесия, С_A , C_B и С_AB - равновесные концентрации веществ А, В и АВ.

Если в равновесную систему ввести или вывести из нее некоторые количества веществ А, В или АВ, изменив тем самым соотношение между концентрациями, то дробь C_A ^/ C_B ^/ /C_AB ^/ (где С^/ - неравновесные концентрации) уже не будет константой равновесия; равновесие окажется нарушенным, и в системе возникнет самопроизвольный процесс, в результате которого установится новое состояние равновесия, когда каждая из равновесных концентраций примет новое численное значение, но соотношение между ними C_A C_B /C_AB останется равным той же самой величине К_с . В этом сущность закона действия масс для химического равновесия.

Состояние химического равновесия при реакции диссоциации можно характеризовать также величиной степени диссоциации a, т.е. долей диссоциированных молекул от общего числа молекул в растворе (0 a 1).

Если в растворе, имеющем объем V, содержится N молей электролита АВ, то при значении степени диссоциации a диссоциации подвергается aN молей АВ и образуется по a·N молей ионов А⁺ и ионов В^- , и остается (1-a)·N недиссоциированных молей АВ. Концентрации компонентов реакции будут равны C_A = C_B = [a·N/V], C_AB = [(1-a)·N/V].

В соответствии с уравнением (I) получим

K_c = [aN/V] [aN/V]/ [(1-a)N/V],

или после преобразования

K_c = a² /(1-a)N/V = a² /(1-a)V_м (2)

Соотношение (2) выражает закон разведения Оствальда. Здесь С - общая (исходная) концентрация электролита АВ в растворе (включая диссоциированные и недиссоциированные молекулы). Обратная концентрации величина V_м , равная V/N, называется разведением (или молярным объёмом) и представляет собою объем, в котором растворен один моль вещества; если концентрация выражена в единицах нормальности (числом моль-эквивалентов в литре), то разведением или эквивалентным объёмом V_Э называется объем, в котором растворен один моль-эквивалент электролита.

Электропроводность есть величина, обратная сопротивлению. Удельной электропроводностью ₀ называется электропроводность одного кубического сантиметра раствора, заключенного между двумя плоскопараллельными электродами, каждый из которых имеет площадь 1см² и находится на расстоянии 1 см друг от друга. Размерность ₀ равна [Ом^-1 см^-1 ]. Удельная электропроводность - величина, обратная удельному сопротивлению. В системе единиц СИ она измеряется в обратных Омах (Ом^-1 ) или Сименсах и выражается в См/м (Сименс на метр).

У 0,1 н раствора KCI при I5^o C ₀ = 0,01046, при 18°С – 0.01116, при 20°С - 0,01164, при 30°С - 0,01410 (Ом^-1 см^-1 ).

Так как измерения проводят при комнатной температуре, при расчётах следует построить вспомогательный график зависимости ₀ от температуры и интерполяцией найти значение ₀ при температуре опыта.

Эквивалентной электропроводностью ( l) называется электропроводность раствора, содержащего моль-эквивалент электролита в объеме V_Э , заключенном между двумя плоскопараллельными электродами, расположенными на расстоянии 1см друг от друга.

Очевидно, при одинаковом расстоянии между электродами число ионов, участвующих в проведении тока, в случае измерения эквивалентной электропроводности в V_Э раз больше, чем при измерении удельной. Поэтому эквивалентная электропроводность равна:

l = ₀ V_э (cм³ /Ом см) = ₀ V_э 10³ (см² /Оммоль). (3)

Аналогично определяется молярная электропроводность ( m) m = k₀ V_м .

Электропроводность l (и m) складывается из величин электропроводностей отдельных ионов, поэтому в проведении электрического тока участвует не всё количество растворенного электролита, а лишь его доля, распавшаяся на ионы. Направленное движение ионов под действием приложенного напряжения, происходящее с постоянной скоростью (электромиграция) накладывается на хаотичное броуновское движение и его скорость зависит от природы ионов и сопротивления среды. Электропроводность раствора электролита складывается из вкладов катионов и анионов. Можно считать, что электропроводность пропорциональна произведению числа ионов и скорости их электромиграции.

При измерении молярной электропроводности общее число ионов равно числу Авогадро, умноженному на степень диссоциации. Считая сопротивление среды не зависящим от концентрации, можно заключить, что молярная электропроводность возрастает с разведением пропорционально увеличению степени диссоциации a и достигает своего максимального значения при a = 1, т.е. при полной диссоциации. То же справедливо для эквивалентной электропроводности. Для слабых электролитов полная диссоциация может быть достигнута лишь при бесконечно большом разведении:

a:1 = m/m = l/l .

Таким образом,

a = m/m = l/l (4)

где m и l - соответственно молярная и эквивалентная электропроводности при бесконечно большом разведении.

При выводе этого соотношения пренебрегли собственной электропроводностью воды, которая основана на слабой диссоциации молекул Н₂ О на ионы H⁺ и OH^- .

Подставляя соотношение (4) в уравнение (2), получаем уравнение

K_c = (l/l )² /(1-l/l )N/V_э (5)

позволяющее вычислить К_с на основании измерения l.

По закону Кольрауша (l )_AB = (l )_A + (l )_B .

Для уксусной кислоты известны значения:

l = l (H⁺ ) + l (CH₃ COO^- )== 387,7 (при 25°С), при 18⁰ С l =350,2, при 100⁰ С l =772 Ом^-1 см² .

Так как измерения проводят при комнатной температуре, необходимо построить вспомогательный график зависимости l от температуры и интерполяцией найти нужное значение l .

Экспериментальная часть

Измерения сопротивления (R) выполняют с помощью цифрового измерителя сопротивления (прибор Е 7-13).

Измерение сопротивления раствора электролита.

На рис. 3 изображена передняя панель универсального измерительного прибора Е 7-13, с помощью которого можно измерить сопротивление растворов электролитов.

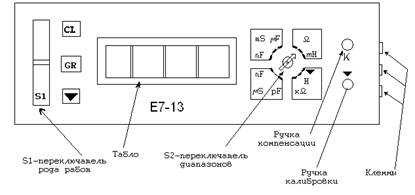
Рис. 3. Передняя панель прибора Е 7-13.

Порядок работы на приборе Е 7-13.

Включть прибор в сеть 220 в (тумблер на задней панели прибора).
Прогреть прибор в течение 10 минут.
Левый рычаг (переключатель S1) перевести в режим настройки ().
Переключатель диапазонов S2 перевести в режим настройки ().
Замкнуть крайние клеммы на правой боковой панели настроечным сопротивлением.
Ручкой компенсации К (правая верхняя ручка) довести показания прибора до 0.
Вынуть сопротивление.
Ручкой калибровки () – правая нижняя ручка – отрегулировать показания прибора до 10.
Левый рычаг (переключатель S1) перевести в режим измерения (GR).
Подсоединить датчик к клеммам на правой панели.
Налить в стаканчик исследуемый раствор и опустить в него датчик. Электроды датчика должны быть погружены в раствор.
Измерение сопротивления раствора в диапазоне (Омы), если измерение невозможно, перевести переключатель диапазонов S2 в положение к (килоОмы).
Отключить датчик, выключить прибор.

Примечание. Пункты с 1 по 7 выполняет лаборант перед началом занятий.

Для измерения электропроводности раствор вливают в сосуд, который предварительно промывают один раз дистиллированной водой и затем два раза раствором, электропроводность которого будет измеряться. При последовательном измерении сопротивления растворов уксусной кислоты, концентрация которых изменяется в два раза, ячейки можно не промывать.

Для каждого измерения следует брать одинаковый объём раствора, так как в проведении тока участвует весь объём раствора, а не только его часть, которая заключена между электродами.

При работе с KCl сопротивление равно нескольким десяткам Ом, а при работе с уксусной кислотой - нескольким тысячам Ом. Удельная электропроводность ₀ пропорциональна измеренной электропроводности (), ₀ =h = h/R_x .

Коэффициент пропорциональности h называется постоянной сосуда, его абсолютная величина зависит от расстояния между электродами и площади поперечного сечения электродов данного сосуда при постоянстве уровня электролита в сосуде. Для его определения нужно измерить в данном сосуде =1/R для эталонного раствора, удельная электропроводность которого заранее известна. В качестве такого раствора берут 0,1н раствор KCI, для которого при 25°С ₀ =0,012815 Ом^-1 см² (при других температурах значения ₀ приведены выше).

При точных измерениях учитывают электропроводность воды.

Следует найти =1/R_x для 0,I н раствора хлористого калия с целью определения h (постоянной сосуда), а затем сделать измерения R_x для нескольких растворов уксусной кислоты различной концентрации.

Оформление работы.

Исходные данные и результаты измерений следует записать в таблицу:

С, Моль-экв/л	V, л/мольэкв	R_x Ом	Ом^-1	₀ Ом^-1 см^-1	l см² /Оммоль-экв	a	K_c моль/л
1/512	512
1/256	256
1/128	128
1/64	64
1/32	32
1/16	16
0/1 н KCl	-				-	-	-

Обработка экспериментальных данных

По данным для KCl вычислить h сосуда (при необходимости использовать интерполяцию литературных данных).
Найти и ₀ для каждого раствора уксусной кислоты.
Определить значение эквивалентной электропроводности уксусной кислоты для всех разведений. Обратить внимание на размерности: объём следует выражать не в л/моль, а в см³ /моль.
Для каждого разведения вычислить a, используя интерполяцию литературных значений l .
Рассчитать К_с для каждого раствора уксусной кислоты.
Определить К_с уксусной кислоты, как среднее из всех найденных значений (для всех концентраций). Полученное значение сравнить с табличным из «Краткого справочника физико-химических величин». Определить относительную ошибку и проанализировать источники ошибок в эксперименте.
Начертить график зависимости, степени диссоциации a от разведения V.

Примечание: Запись вычислений в лабораторном журнале должна быть достаточно полной для возможности проверки правильности рассчитанных значений, приведённых в таблице.

Для защиты работы необходимо знать:

- Что такое электролитическая диссоциация, какова ее движущая сила, от каких факторов зависит?

- Количественные меры диссоциации.

- Сильные и слабые электролиты; зависит ли сила электролита от свойств растворителя и от каких именно.

- Закон разведения Оствальда.

- Удельная и эквивалентная электропроводность, их зависимость от концентрации.

- Обосновать формулу: a = l/l₀ .

- Закон Кольрауша

- Что такое кондуктометрия?

Правила расчётов с приближёнными числами

- Надо знать, что практически все величины, используемые в науке и технике, являются приближёнными. Недопустимо огрублять результат измерений и расчётов с измеряемыми величинами; с другой стороны, результат необходимо правильно округлять, так как представление величины числом с большим количеством цифр (которое высвечивается на экране калькулятора) может вызвать сомнения относительно грамотности студента. Правила округления приведены ниже.

- Число знаков в результате, полученном при измерении, должно указывать на точность измерений, причём предпоследняя цифра должна быть точной, а последняя приближённой.

- При сложении и вычитании, умножении и делении сохраняют в результате столько значащих цифр, сколько имеется в числе, измеренном с наименьшей точностью (значащие цифры отсчитываются от первой ненулевой слева; например, в числе 0.0543 три значащих цифры).

- При возведении в степень и извлечении корня сохраняют в результате столько значащих цифр, сколько их имеется в возводимом в степень или подкоренном числе.

- При логарифмировании сохраняют в мантиссе столько значащих цифр, сколько их имеется в логарифмируемом числе.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Киреев В.А. Курс физической химии. М.: Химия, 1975. С. 543-555, 626-658, 667-699.

2. Краткий справочник физико-химических величин. /Под ред А.А.Равделя и А.М.Пономаревой. М.: Химия, 1997. С

ОГЛАВЛЕНИЕ

Лабораторная работа 1………………………………….

Кинетика каталитической реакции разложения

перекиси водорода

Лабораторная работа 2…………………………………..

Определение степени и константы диссоциации

слабой кислоты кондуктометрическим методом

Скачать архив с текстом документа