Методы нулевого порядка минимизации функций многих переменных. Постановка задачи. Описание метод

СОДЕРЖАНИЕ: Министерство образования РБ Учреждение образования Белорусский государственный университет Информатики и радиоэлектроники Кафедра радиотехнических систем

Министерство образования РБ

Учреждение образования

Белорусский государственный университет

Информатики и радиоэлектроники

Кафедра радиотехнических систем

Реферат по дисциплине

Основы информационных технологий

«Методы нулевого порядка минимизации функций многих переменных. Постановка задачи. Описание метода. Преимущества и недостатки метода.»

Выполнил Проверил

магистрант группы Синицин А.К.

Минск 2010
СОДЕРЖАНИЕ

1. Постановка задачи…………………………………………………….	3
2. Обзор основных методов……………………………………………...	4
2.1 Метод прямого поиска (метод Хука-Дживса)...……………………	5
2.2 Метод деформируемого многогранника (метод Нелдера-Мида)....	7
2.3 Метод полного перебора (метод сеток)………………………….…	9
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ………………………..	11

1. Постановка задачи.

Задачи о нахождение минимума функций одной или многих переменных являются весьма распространенными. Развитые для этой цели методы позволяют также находить решения систем уравнений. Методы нахождения минимума разделяют на методы 0-го, 1-го, 2-го и т.д. порядка. Наибольшей популярностью, при решении задач такого рода на компьютере, пользуются методы 0-го порядка для нахождения минимума функции, которые используют лишь значения этой функции.

В этих методах для определения направления спуска не требуется вычислять производные целевой функции. Направление минимизации в данном случае полностью определяется последовательными вычислениями значений функции. Следует отметить, что при решении задач безусловной минимизации методы первого и второго порядков обладают, как правило, более высокой скоростью сходимости, чем методы нулевого порядка. Однако на практике вычисление первых и вторых производных функции большого количества переменных весьма трудоемко. В ряде случаев они не могут быть получены в виде аналитических функций. Определение производных с помощью различных численных методов осуществляется с ошибками, которые могут ограничить применение таких методов. Кроме того, на практике встречаются задачи, решение которых возможно лишь с помощью методов нулевого порядка, например задачи минимизации функций с разрывными первыми производными. Критерий оптимальности может быть задан не в явном виде, а системой уравнений. В этом случае аналитическое или численное определение производных становится очень сложным, а иногда невозможным. Для решения таких практических задач оптимизации могут быть успешно применены методы нулевого порядка. Рассмотрим некоторые из них для минимизации функций многих переменных

y = f ( x 1 ,...,xn ) = f ( x ) (1)

2. Обзор основных методов.

Практически все существующие методы по способу достижения поставленной задачи можно разбить на две большие группы:

а. Метод перебора. Как и в случае функций одной переменной, метод сводится к расчету набора значений функции в некоторой области и выбору минимального значения. Метод позволяет найти глобальный минимум функции. Для задач с высокой размерностью приводит к недопустимо большому количеству вычислений.

б. Симплекс-метод . Это своеобразный метод нулевого порядка, основанный на построении симплекса – множества равноудаленных точек, в количестве на единицу превышающем размерность пространства. В двумерном случае симплекс – это равносторонний треугольник. В трехмерном случае – правильная треугольная пирамида. На начальном шаге итерационного процесса даются координаты исходного симплекса и в них рассчитываются значения минимизируемой функции. Среди вершин симплекса находится та, в которой функция имеет наибольшее значение. Для построения нового симплекса эта вершина отбрасывается. Вместо нее выбирается новая вершина, симметрично отраженная от плоскости, проведенной через остальные вершины. В новой вершине рассчитывается значение функции. В старых же вершинах, вошедших в новый симплекс, значения функции уже известны. Снова находится вершина, в которой функция имеет наибольшее значение. И так далее. Ключевым моментом является то, что на каждом шаге итерационного процесса требуется расчет функции лишь в одной точке. Для минимизации функций в многомерных пространствах это оказывается очень важным.

2.1 Метод прямого поиска (метод Хука-Дживса)

Метод был разработан в 1961 году, но до сих пор является весьма эффективным и оригинальным. На разработку методов прямого поиска для определения минимума функций и переменных было затрачено много усилий. Методы прямого поиска являются методами, в которых используются только значения функции. Практика показала, что этот метод эффективен и применим для широкого числа приложений. Рассмотрим функцию двух переменных. Ее линии постоянного уровня на рисунке 1, а минимум лежит в точке (x₁ ^* , x₂ ^* ).

Простейшим методом поиска является метод покоординатного спуска. Из точки А мы производим поиск минимума вдоль направления оси и , таким образом, находим точку В, в которой касательная к линии постоянного уровня параллельна оси . Затем, производя поиск из точки В в направлении оси , получаем точку С, производя поиск параллельно оси , получаем точку D, и т. д. В выбранном направлении осуществляют спуск до тех пор, пока значение функции уменьшается. После того как в данном направлении не удается найти точку с меньшим значением функции, уменьшают величину шага спуска. Если последовательные дробления шага не приводят к уменьшению функции, от выбранного направления спуска отказываются и осуществляют новое обследование окрестности и т. д.

Рисунок 1 – Нахождение минимума функции двух переменных

Достоинством метода прямого поиска является простота его программирования на компьютере. Он не требует знания целевой функции в явном виде, а также легко учитывает ограничения на отдельные переменные, а также сложные ограничения на область поиска.

Недостаток метода прямого поиска состоит в том, что в случае сильно вытянутых, изогнутых или обладающих острыми углами линий уровня целевой функции он может оказаться неспособным обеспечить продвижение к точке минимума. Действительно, в случаях, изображенных на рисунке 2, а и б, каким бы малым ни брать шаг в направлении х₁ или x₂ из точки х’ нельзя получить уменьшения значения целевой функции.

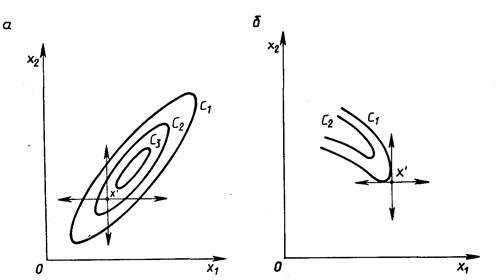
Рисунок 2 – Прямой поиск: невозможность продвижения к минимуму:

а – С1 C2 C3; б - С1 C2

Блок-схема данного метода:

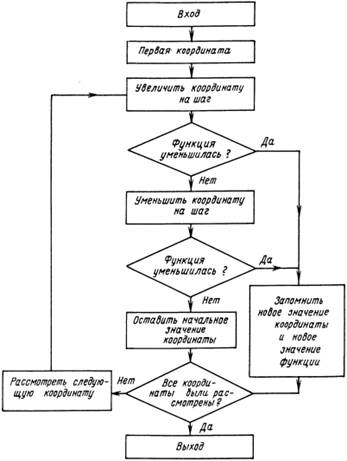
Рисунок 3 – Блок-схема метода Хука-Дживса

2.2 Метод деформируемого многогранника (метод Нелдера-Мида)

Метод Нелдера-Мида, также известный как метод деформируемого многогранника и симплекс-метод, – метод безусловной оптимизации функции от нескольких переменных, не использующий производной функции, поэтому легко применим к негладким и зашумлённым функциям.

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.

Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс. Более развитый подход к исключению локальных экстремумов предлагается в алгоритмах, основанных на методе Монте-Карло, а также в эволюционных алгоритмах.

Пусть требуется найти безусловный минимум функции n переменных . Предполагается, что серьёзных ограничений на область определения функции нет, то есть функция определена во всех встречающихся точках.

Параметрами метода являются:

1) коэффициент отражения 0, обычно выбирается равным 1.

2) коэффициент сжатия 0, обычно выбирается равным 0,5.

3) коэффициент растяжения 0, обычно выбирается равным 2.

Алгоритм данного метода такой:

1. «Подготовка». Вначале выбирается n + 1 точка , образующие симплекс n-мерного пространства. В этих точках вычисляются значения функции: .

2. «Сортировка». Из вершин симплекса выбираем три точки: x_h с наибольшим (из выбранных) значением функции f_h , x_g со следующим по величине значением f_g и x_l с наименьшим значением функции f_l . Целью дальнейших манипуляций будет уменьшение по крайней мере f_h .

3. Найдём центр тяжести всех точек, за исключением x_h : . Вычислять f_c = f(x_c ) не обязательно.

4. «Отражение». Отразим точку x_h относительно x_c с коэффициентом (при = 1 это будет центральная симметрия, в общем случае — гомотетия), получим точку x_r и вычислим в ней функцию: f_r = f(x_r ). Координаты новой точки вычисляются по формуле:

x_r = (1 + )x_c x_h (2)

5. Далее смотрим, насколько нам удалось уменьшить функцию, ищем место f_r в ряду f_h ,f_g ,f_l .

Если f_r f_l , то направление выбрано удачное и можно попробовать увеличить шаг. Производим «растяжение». Новая точка x_e = (1 )x_c + x_r и значение функции f_e = f(x_e ).

Если f_e f_l , то можно расширить симплекс до этой точки: присваиваем точке xh значение xe и заканчиваем итерацию (на шаг 9).

Если f_e f_l , то переместились слишком далеко: присваиваем точке x_h значение x_r и заканчиваем итерацию (на шаг 9).

Если f_l f_r f_g , то выбор точки неплохой (новая лучше двух прежних). Присваиваем точке x_h значение x_r и переходим на шаг 9.

Если f_h f_r f_g , то меняем местами значения x_r и x_h . Также нужно поменять местами значения f_r и f_h . После этого идём на шаг 6.

Если f_r f_h , то просто идём на следующий шаг 6.

В результате (возможно, после переобозначения) f_r f_h f_g f_l .

6. «Сжатие». Строим точку x_s = x_h + (1 )x_c и вычисляем в ней значение f_s = f(x_s ).

7. Если f_s f_h , то присваиваем точке x_h значение x_s и идём на шаг 9.

8. Если f_s f_h , то первоначальные точки оказались самыми удачными. Делаем «глобальное сжатие» симплекса — гомотетию к точке с наименьшим значением x_l :

(3)

9. Последний шаг — проверка сходимости. Может выполняться по-разному, например, оценкой дисперсии набора точек. Суть проверки заключается в том, чтобы проверить взаимную близость полученных вершин симплекса, что предполагает и близость их к искомому минимуму. Если требуемая точность ещё не достигнута, можно продолжить итерации с шага 2.

2.1 Метод полного перебора (метод сеток)

Многомерные задачи, естественно, являются более сложными и трудоемкими, чем одномерные, причем обычно трудности при их решении возрастают при увеличении размерности. Возьмем самый простой по своей идее приближенный метод поиска наименьшего значения функции. Покроем рассматриваемую область сеткой G с шагом h (рисунок 4) и определим значения функции в ее узлах. Сравнивая полученные числа между собой, найдем среди них наименьшее и примем его приближенно за наименьшее значение функции для всей области.

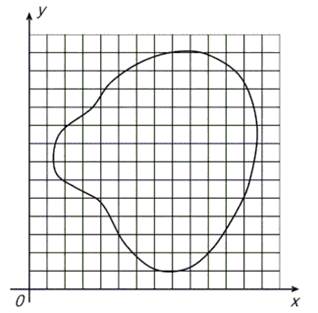
Рисунок 4 – Покрытие рассматриваемой области сеткой G с шагом h

Данный метод используется для решения одномерных задач. Иногда он применяется также для решения двумерных, реже трехмерных задач. Однако для задач большей размерности он практически непригоден из-за слишком большого времени, необходимого для проведения расчетов. Действительно, предположим, что целевая функция зависит от пяти переменных, а область определения G является пятимерным кубом, каждую сторону которого при построении сетки мы делим на 40 частей. Тогда общее число узлов сетки будет равно 41⁵ 10⁸ . Пусть вычисление значения функции в одной точке требует 1000 арифметических операций (это немного для функции пяти переменных). В таком случае общее число операций составит 10₁₁ . Если в нашем распоряжении имеется ЭВМ с быстродействием 1 млн. операций в секунду, то для решения задачи с помощью данного метода потребуется 10⁵ секунд, что превышает сутки непрерывной работы. Добавление еще одной независимой переменной увеличит это время в 40 раз. Проведенная оценка показывает, что для больших задач оптимизации метод сплошного перебора непригоден. Иногда сплошной перебор заменяют случайным поиском. В этом случае точки сетки просматриваются не подряд, а в случайном порядке. В результате поиск наименьшего значения целевой функции существенно ускоряется, но теряет свою надежность.

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1. Ю.В. Губарь «Введение в математическое программирование», ИНТУИТ

2. А.Г.Трифонов «Постановка задачи оптимизации и численные методы ее решения», Консультационный Центр MATLAB

3. Материалы интернет портала «Википедия»: http://ru.wikipedia.org/

4. Н.Н. Калинкин «Численные методы», 1978 г., Наука

Скачать архив с текстом документа