Многофакторные экономико-математические модели прогнозирования инфляции

СОДЕРЖАНИЕ: Содержание Введение Глава 1. Многофакторные модели прогнозирования 1.1 Расчет параметров уравнений по отклонениям 1.2 Характеристика тесноты связи

Содержание

Введение

Глава 1. Многофакторные модели прогнозирования

1.1 Расчет параметров уравнений по отклонениям

1.2 Характеристика тесноты связи

1.3 Прогнозирование по абсолютным уровням временных рядов3

1.4 Расширение линейной множественной регрессии3

Глава 2. Инфляция как многофакторный процесс3

2.1 Общий вид многофакторной модели прогнозирование инфляции3

2.2 Факторы, влияющие на уровень инфляции3

Глава 3. Моделирование и прогнозирование уровня инфляции на примере Украины3

Заключение3

Список литературы

Введение

В настоящее время проблема инфляции является одной из самых важных и чрезвычайно актуальных. Она затрагивает абсолютно всех – и население, и предприятия, и органы государственной власти.

Вопросами анализа инфляционных процессов занимались многие зарубежные и отечественные ученые-экономисты. Весомый вклад в развитие теории инфляции внесли Моисеев С.Р., Галиченко О.Г., Камаев В.Д., Предборский В.А., Усов В.В, Долан Э.Дж., Линдсей Д.Э. и др. Однако некоторые вопросы данной проблемы остаются еще недостаточно раскрытыми. Так, не полностью освещенными остаются вопросы моделирования и прогнозирования уровня инфляции.

Целью работы является изучение многофакторных экономико-математических моделей, проведение комплексного анализа инфляционных процессов.

В соответствии с целью работы необходимо решить следующие задачи:

•выделить наиболее существенные факторы, влияющие на уровень инфляции;

•проанализировать многофакторную корреляционно-регрессионную модель уровня инфляции;

•рассмотреть пример прогнозирования уровня инфляции на практике.

Учитывая, что инфляция происходит в силу влияния множества факторов, целесообразно прогнозные расчеты осуществлять на основе многофакторных моделей с применением корреляционно-регрессионного метода, позволяющего установить наличие корреляционной связи между прогнозируемой инфляцией и влияющими на нее факторами, определить форму связи, сформировать уравнение и на его основе осуществить прогноз инфляции.

Для решения вышеуказанных задач в работе были применены как общенаучные, так и специальные методы познания. Из общенаучных методов – это методы системного анализа, обобщения и формализации. Из специальных – методы обобщающих показателей, анализа рядов динамики, множественного и парного корреляционно-регрессионного анализа, статистического прогнозирования на основе трендовых и авторегрессионных моделей.

1. Многофакторные модели прогнозирования

Сложный характер экономико-математических процессов ставит задачу отбора наиболее существенных факторов, оказывающих влияние на вариацию исследуемых характеристик. Таких факторов достаточно много ввиду усложнения и неоднозначности экономической динамики. Тренды и уравнения парной регрессии имеют ограниченные возможности.

В регрессионном анализе, проводимом в пространстве, при наличии достаточного числа наблюдений, в соответствии с предпосылками, применяются многофакторные модели, или уравнения множественной регрессии.

Они позволяют детально исследовать взаимозависимость признаков, их соподчиненность и силу корреляционного взаимодействия. Эта тема достаточно глубоко рассматривается в курсе многомерного статистического анализа и в то же время она является темой факторного анализа пространственно-временной информации.

Множественная корреляция исследует статистическую зависимость результативного признака от нескольких факторных признаков. В общем виде уравнение регрессии имеет вид:

y_t = f ( x ₁ _t , x ₂ _t ,…, x_pt )+ _t ,

где t = 1,2,...n – количество наблюдений, р – количество параметров, _t – возмущающая переменная.

Для линейной зависимости:

y_t = ^p _j ₌₁ a_j x_jt + _t , t = 1,2,...n.

Выбор уравнения множественной регрессии включает следующие этапы:

· отбор факторов-аргументов;

· выбор уравнения связи;

· определение числа наблюдений, необходимых для получения несмещенных оценок.

Одним из важнейших требований является отбор наиболее существенных факторов. Также необходим традиционный экономический анализ, в ходе которого глубже и полнее выявляется существо, направленность и теснота связи между факторами. Последовательное введение всех конкурирующих факторов в уравнение регрессии следует осуществлять с точки зрения минимизации остаточной дисперсии.

В процессе отбора факторных признаков особое внимание следует уделять выявлению и устранению мультиколлинеарности – тесной корреляционной связи между двумя (коллинеарности) и большим числом факторных признаков.

Если в модель включаются две или несколько связанных между собой «независимых» переменных, то система нормальных уравнений не имеет однозначного решения, наряду с уравнением регрессии существуют и другие линейные соотношения.

Последствия мультиколлинеарности:

· слабая обусловленность матрицы системы нормальных уравнений;

· неопределенное множество коэффициентов регрессии а_j ;

· сильная корреляция стандартных ошибок параметров и возрастание остаточных дисперсий;

· чувствительность коэффициентов регрессии к выборке.

Разрешение проблемы мультиколлинеарности можно разбить на несколько этапов:

1. Установление самого факта существования мультиколлинеарности.

2. Измерение степени мультиколлинеарности.

3. Определение области мультиколлинеарности на множестве независимых переменных.

4. Установление причин мультиколлинеарности.

5. Определение мер по устранению мультиколлинеарности.

Существует несколько методов выявления мультиколлинеарности, основанных на следующих процедурах:

a) анализ парных коэффициентов корреляции между независимыми переменными r_xixj ;

b) анализ множественных коэффициентов корреляции каждой из независимых переменных со всеми остальными;

c) сравнение парных коэффициентов корреляции между независимыми переменными с парными коэффициентами между зависимой и независимыми переменными r_xixj , r_yxi ;

d) сравнение множественненных коэффициентов корреляции между независимыми переменными с коэффициентом множественной корреляции между зависимой переменной со всеми остальными.

Наряду с линейными моделями используются нелинейные зависимости, например, степенная зависимость:

y^t _c = a ₀ x ₁ _t ^a ¹ x ₂ _t ^a ² … x_pt ^ap ,

которую путем простейших преобразований можно привести к линейному виду:

ln_yt =ln_a0 +a₁ lnx_1t +a₂ lnx_2t +…+a_p lnx_pt .

Анализ временных рядов с учетом предпосылок регрессионного анализа позволяет определить общую направленность в процессе прогнозирования изменения величины исследуемого показателя. Для исключения автокорреляции при необходимости используются рассмотренные выше процедуры для случая парной зависимости. Могут использоваться две вычислительные схемы прогнозирования на основе уравнений множественной регрессии:

1) анализ отклонений абсолютных уровней от трендов;

2) построение нескольких статических моделей (для каждого года предпрогнозного периода), параметры которых определяются в виде функций времени, после чего рассчитываются наиболее вероятные значения признаков в перспективе.

1.1 Расчет параметров уравнений по отклонениям

Осуществляется отбор факторных признаков x₁ ,x₂ ,... x_p , оказывающих влияние на y. Исходные данные представлены временными рядами

x ₁ _t ,x₂ _y ,... x_pt ; y_t .

Определяются тенденции изменения временных рядов, т.е. тренды

y_t ^c =f(t); x_it ^c =f_i (t); i=1,2,…,n.

Рассчитываются отклонения выравненных значений переменных от исходных величин

_t =y_t -f (t); _it =x_it – f_i (t).

Выявляется наличие мультиколлинеарности, для чего вычисляются коэффициенты парной корреляции. Устанавливаются периоды запаздывания (временные лаги) во взаимодействии признаков.

После корректировки состава независимых переменных приступают к оцениванию параметров уравнения множественной линейной регрессии

y_t = ₁ ₁ _t + ₂ ₂ _t +... + _p _pt . (*).

При наличии временного лага L по переменной х_i в уравнение вместо е _it вводится е _it _- _L .

Коэффициенты б_i рекомендуется определять по методу наименьших квадратов, используя так называемые стандартизованные в _i коэффициенты. Необходимость использования коэффициентов в стандартизованном виде объясняется тем, что в уравнении (*) каждое отклонение является абсолютной величиной, такой же, как и исходные временные ряды зависимой и независимой переменных. Числовые значения отклонений представлены в соответствующих единицах измерения.

Данное обстоятельство не позволяет оценивать сравнительную силу воздействия каждого аргумента на зависимую переменную путем сопоставления коэффициентов регрессии ₁ , ₂ ,…, _p .

Переход к стандартизованным коэффициентам заключается в замене отклонений _t , _it новыми переменными, исходя из соотношений

T = _t / _t ; T_i = _it / _it ,

откуда _t = T _t ; _it = T_i _it . Подставив последние выражения в уравнение (*) и поделив левую и правую части на _t , получим:

T =( ₁ T ₁ ₁ _t / _t )+( ₂ T ₂ ₂ _t / _t )+…+( _p T_p _pt / _t ).

Переменные Т в последнем уравнении являются теперь относительными безразмерными величинами. Замена _i _it / _t на _i приводит уравнение к стандартизованному виду

T = ₁ T ₁ + ₂ T ₂ +…+ _p T_p ,

в котором _i - стандартизованные коэффициенты регрессии. Они показывают, на сколько среднеквадратических отклонений изменится зависимая переменная, если величина i -го независимого фактора увеличится или уменьшится на одно свое среднеквадратическое отклонение при условии постоянства всех остальных факторов-аргументов.

Так как _i -коэффициенты являются относительными величинами, то с их помощью можно сделать вывод о степени влияния каждого фактора на функцию.

Численные значения коэффициентов определяются на основе значений коэффициентов парной корреляции.

Система нормальных уравнений, используемых при расчетах, имеет вид:

r_t ₁ _t = ₁ r ₁ _t ₁ _t + ₂ r ₁ _t ₂ _t +…+ _p r ₁ _tpt

r_t ₂ _t = ₁ r ₂ _t ₁ _t + ₂ r ₂ _t ₂ _t +…+ _p r ₂ _tpt ,

…………………………………………

r_tpt = ₁ r_pt ₁ _t + ₂ r_pt ₂ _t +…+ _p r_ptpt

r_tit = _it /( ² _t ² _it ) ; r_itjt = _it _jt /( ² _it ² _jt ) ; r_itjt =1.

Система уравнений, линейных относительно _i , может быть решена любым способом. Естественно, оценка параметров и проверка надежности найденных уравнений регрессии осуществляются при использовании Microsoft Excel и множества статистических пакетов обработки данных, таких как SPSS, Statistica, Minitab и других. В данном случае важен содержательный алгоритм расчетов. Например, при использовании формул Крамера в _i = _i /, где _i – определитель, получаемый из главного определителя путем замены i- го столбца столбцом из свободных членов.

После решения системы и определения _i -коэффициентов находятся коэффициенты _i = _i _t / _it , осуществляется переход от относительных величин к абсолютным и уравнению

y_t = ^p _j ₌₁ a_j x_jt + _t , t =1,2,… n .

Для оценки параметров уравнения временные ряды должны быть не менее 15-20 лет, а прогнозный период в 2-3 раза короче. Прогнозные значения x_jt можно оценить на основе экстраполяции, методом экспоненциального сглаживания, на основе трендов или уравнений авторегрессии, методом экспертных оценок. При необходимости в модели должны найти отражение периоды запаздывания.

1.2 Характеристика тесноты связи

Для определения тесноты связи рассчитывается коэффициент множественной корреляции R , 0 R 1 . R не присваивается знак, т.к. факторы находятся в разной парной (прямой и обратной) зависимости с результативной переменной.

Для уравнений регрессии в стандартизованном масштабе при линейной зависимости R имеет вид:

R=(в₁ r_г _t _е1 _t + в₂ r_г _t _е2 _t +…+ в_p r_г _t _е _pt )^Ѕ .

Для определения степени влияния вариации факторных признаков на вариацию зависимого признака рассчитывается коэффициент множественной детерминации D = R ² , частные коэффициенты детерминации

d_i = _i r_t ₁ _t ; d_i = R ² .

Для случаев нелинейной зависимости коэффициент множественной корреляции рассчитывается как результат сопоставления двух дисперсий: остаточной ² _ост и общей ² _общ .

Проверка статистической надежности уравнения множественной регрессии. В регрессионном анализе при использовании в качестве первичной информации выборочных данных результаты расчетов в значительной степени зависят от способности выборочного уравнения регрессии отображать закономерности, существующие в генеральной совокупности. Важное значение при этом имеет правильный выбор типа аналитической функции, качество подбора параметров множественного уравнения, степень разброса исходных данных относительно линии регрессии.

Для оценки статистической надежности множественных моделей могут применяться различные показатели, особое место среди них занимают t -критерий Стьюдента и F -критерий Фишера.

Для проверки существенности коэффициентов регрессии определяется расчетное значение t -критерия

которое сопоставляется с табличным значением t _табл . Величина t _табл находится с учетом числа степеней свободы k = n - p -1 , где n – количество наблюдений, p – количество факторов и доверительной вероятности P . Если t_p _асч t _табл ., то это свидетельствует о том, что корреляционная связь существует между признаками у _t и x ₁ _t , x ₂ _t ,...,x_pt не только в выборочной, но и в генеральной совокупности.

Значимость коэффициентов чистой регрессии устанавливается следующим образом. Определяется расчетная величина t -критерия для каждого i - го коэффициента, которая сравнивается с табличной.

, где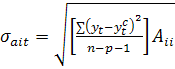

где А_ii – диагональный элемент матрицы, обратной по отношению к матрице системы нормальных уравнений. Если t_расч t_табл , то значение i -го коэффициента пропорциональности в выборочном уравнении регрессии незначительно отличается от коэффициента регрессии, которое можно было бы построить по материалам всей совокупности. В противном случае надежность i -го коэффициента следует считать недостаточной, а соответствующий факторный признак x_it рекомендуется исключить из числа переменных в уравнении регрессии.

При необходимости по известным t_табл , _ait можно рассчитать доверительную зону для выборочного коэффициента:

а^в ⁽ ^н ⁾ _it =a_it ±t _табл _ait .

Для оценки надежности уравнения регрессии в целом рекомендуется использовать F -критерий Фишера.

Если F _расч F _табл , для k ₁ =р-1 и k ₂ = n - p и доверительной вероятности P , то уравнение множественной регрессии следует признать статистически значимым. В противном случае гипотеза об адекватности уравнения отбрасывается.

Также для обобщенной оценки уравнения множественной регрессии определяется средняя ошибка аппроксимации:

Допустимой ошибкой является ошибка, не превышающая 15%.

1.3 Прогнозирование по абсолютным уровням временных рядов

Для исключения автокорреляции непрерывный процесс изменения признака искусственно расчленяется на несколько этапов по числу отрезков времени, составляющих период наблюдения.

На каждой стадии расчетов значения переменных рассматриваются как статические величины без учета их вероятного изменения в будущем. По исходным данным, характеризующим взаимодействие признаков в каждый данный момент времени, строятся уравнения множественной регрессии

y_t ^c =a_0t +a_1t x_1t +a_2t x_2t +…+ a_pt x_pt либо y⁾ _t =a_0t x^a1t _1t x^a2t _2t …x^apt _pt .

Поскольку значения переменных x ₁ _t , х₂ _t ,..., x_pt не остаются постоянными во времени, а закономерно изменяются, то множество моделей необходимо дополнить аналитическими зависимостями, отражающими тенденции варьирования показателей аргументов х _it и коэффициентов регрессии а _it . С этой целью коэффициенты пропорциональности объединяют во временные ряды, после чего устанавливают закономерности изменения их во времени. В общем случае уравнения регрессии имеют вид:

Аналогично определяется тенденция варьирования для каждого показателя аргумента в отдельности:

С помощью этих моделей могут быть найдены значения переменных x^T ₁ _t , x^T ₂ _t ,..., x^T _pt , а также коэффициенты a^T ₁ _t , a^T ₂ _t ,..., a^T _pt ,. Для прогнозирования величины исследуемого признака могут использоваться регрессии вида

Зависимость может быть мультипликативной. Модели могут использоваться в динамике. Для этого в уравнение регрессии подставляются прогнозные уровни аргументов и параметров.

Доверительные интервалы должны учитывать вариацию аргументов и вариацию коэффициентов регрессии.

1.4 Расширение линейной множественной регрессии

В уравнение регрессии обычно включаются переменные х , существенные с точки зрения экономической теории и принимающие значения в некотором интервале. Некоторые из них в свою очередь могут быть функциями других переменных. Например, , а x _j =lgz _j и т.п. Модель при этом должна оставаться линейной относительно ее параметров и удовлетворять всем свойствам, необходимым для применения обыкновенного метода наименьших квадратов.

При изучении социально-экономических явлений в некоторых случаях необходимо включить в модель такие факторы, которые отражают, в том числе, различные качественные уровни. Это имеет место при существенных изменениях общих условий, при временном сдвиге, анализе атрибутивных признаков, таких, например, как пол, образование, принадлежность к социальным или профессиональным группам и т.д. Иногда это связано с потребностью изучения большого числа количественных переменных.

Такие специальным образом сконструированные переменные называются фиктивными переменными. Эти переменные вводятся в модель и оцениваются, однако им должны быть присвоены при этом некие цифровые метки, осуществляющие преобразование качественных переменных в количественные.

Рассмотрим пример функции спроса на кредитные услуги банков. Пусть имеет место линейная зависимость потребления таких услуг по сельским и городским домохозяйствам в зависимости от доходов. В общем виде для обследуемой совокупности уравнение регрессии имеет вид:

y=a+bx+е ,

где y – величина обязательств (долга) по кредитам, х – доход на одного члена семьи. Аналогичные уравнения можно найти отдельно для домохозяйств на селе и в городе: y₁ =a₁ +b₁ x₁ +е₁ и y₂ =a₂ +b₂ x₂ +е₂ . Различия обусловлены особенностями ведения домашнего хозяйства, психологией сельских и городских жителей, определяющих в конечном счете их кредитное поведение. Средние характеристики объемов обязательств городских и сельских домохозяйств y₁ и у будут различными.

Объединение уравнений у₁ и у₂ возможно с включением фиктивных переменных:

y = a ₁ z ₁ + a ₂ z ₂ + bx +е , (**)

где z ₁ и z ₂ – фиктивные переменные места проживания домохозяйства, такие, что:

1 – город

z₁ =

0 – село

1 – село

z₁ =

0 – город

Зависимая переменная y в уравнении (**) является функцией не только дохода х , но и типа домохозяйства (городского или сельского) (z₁ , z₂ ). Переменная z рассматривается как дихотомическая, переменная, принимающая два значения: 1 и 0. Когда z₁ =1, z₂ =0 и, наоборот, при z₁ =0 , z₂ =1 .

Общее уравнение регрессии (**) для городского домохозяйства будет иметь вид: y^с =a₁ +bx . Для сельского домохозяйства соответственно уравнение регрессии принимает вид: y^с =a2+bx . Параметр b является общим для всей совокупности домохозяйств, а различия кредитного поведения городских и сельских семей обусловлены свободными членами уравнения регрессии.

Матрица исходных данных будет иметь вид:

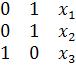
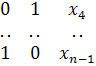
В соответствии с приведенной матрицей первые два домохозяйства в исследуемой совокупности являются сельскими, следующее – городское, следующее – сельское и т.д., наконец, два последних из n являются городскими. Для оценки параметров уравнения может использоваться метод наименьших квадратов.

Фиктивных переменных может быть введено более двух групп, что позволяет углубить исследование. В рассмотренном примере кредитное поведение домохозяйств будет зависеть, например, от объема накопленных активов, возраста главы семьи, наличия и количества детей и т.п.

Пример подобного подхода приведен Дж. Джонстоном. Описано изучение динамики социально-экономических систем на основе совместного анализа социологических и некоторых других переменных с традиционными экономическими переменными.

В исследовании распределения семей по признаку долга по закладным задача разбита на две части. Вначале предсказывается вероятность наличия долга, а затем для семей с ненулевым долгом предсказывается его величина.

2. Инфляция как многофакторный процесс

2.1 Общий вид многофакторной модели прогнозирование инфляции

J_n = f ( x ₁ , x ₂ ,…, x_n ).

Среди важнейших факторов следует выделить: изменение курса валюты, рост денежной массы, изменение ставки рефинансирования национального банка. При этом по каждому фактору необходимо учитывать временной лаг. При изменении ситуации временной лаг меняется. Изменчивость временного лага является одним из фундаментальных макроэкономических факторов. Знание временной связи между инфляцией и ее факторами позволяет осуществить более точное прогнозирование инфляционных процессов и умело управлять ими.

В мировой практике распространенным методом прогнозировании инфляции является расчет ее уровня на основе дефлятора ВВП. Сущность этого метода состоит в следующем. На основе данных по инфляции в предшествующем периоде и учета влияния факторов в прогнозируемом периоде определяется инфляции на определенный прогнозируемый период. Выделяются следующие факторы: изменение денежных доходов, субсидий, экспортных и импортных цен ближнего и дальнего зарубежья. процентных ставок по кредитам и депозитам и др. Схема методики расчета уровня инфляции подставлена в табл.

Таблица 1. Расчет уровня инфляции

Номер

п/п

Показатели (факторы)

Обозначение

Изменение инфляции, %

Инфляция в предшествующем периоде

Изменение денежных доходов

Изменение субсидий

Изменение импортных цен

Изменение экспортных цен

Изменение процентной ставки

Инфляция в прогнозируемом периоде

J^t

СБ,

ИЦ

ЭЦ

ПС

J^t ⁺¹

Конкретное значение

(DD^t /ВВП^t )*(DD^t ⁺¹ -DD^t )

(СБ^t /ВВП^t )*(СБ^t ⁺¹ -СБ^t )

(И^t /ВВП^t )*(ИЦ^t ⁺¹ -ИЦ^t )

(Э^t /ВВП^t )*(ЭЦ^t ⁺¹ -ЭЦ^t )

(ЧОП^t /ВВП^t )*(ПС^t ⁺¹ -ПС^t )

1+2+3+4+5+6

Примечание. t – предшествующий период: (t+1) – прогнозируемый период; И – импорт; Э – экспорт; ЧОП – чистый остаточный продукт.

По каждому фактору определяются его прогнозируемая величина и изменение. Затем данные в абсолютном выражении по соответствующему фактору в периоде, предшествующем прогнозируемому, делятся на ВВП в том же периоде и этот результат умножается на процентное изменение фактора в прогнозируемом периоде по сравнению с предшествующим.

Результаты по каждому фактору суммируются и, исходя из уровня инфляции предшествующего периода и влияния факторов, рассчитывается инфляция в прогнозируемом периоде.

Поскольку инфляционные процессы проявляются при росте цен, прогнозирование инфляции должно осуществляться в сочетании с прогнозированием индексов цен.

Индекс роста цен J_p можно представить как соотношение индексов денежной массы J_m , скорости денежного обращения J_u и реального ВВП J_Q :

J_p =(J_m *J_u )/J_Q .

2.2 Факторы, влияющие на уровень инфляции

Современная инфляция находится под воздействием не только денежных, но и неденежных факторов. Денежные факторы вызывают превышение денежного спроса над товарными предложением, в результате чего происходит нарушение требований закона денежного обращения. Неденежные факторы ведут к первоначальному росту издержек и цен товаров, поддерживаемому последующим подтягиванием денежной массы к их возросшему уровню. Обе группы факторов переплетаются и взаимодействуют друг с другом, вызывая рост цен на товары и услуги, или инфляцию.

В то же время увеличение внешней задолженности вызывает появление фактора усиления инфляции – так называемой долларизации. Данный процесс связан и привилегированным положением доллара или другой сильной валюты перед национальной валютой, а это не только не стимулирует приток иностранных инвестиций, но и приводит к бегству капиталов из страны.

Одним из денежных факторов, влияющих на инфляцию, является денежная масса, изменение объема которой зависит от многих факторов, как общеэкономических (циклического развития экономики, темпов экономического роста, движения цен), так и чисто монетарных (структуры платежного оборота, развития кредитных операций и взаимных расчетов, уровня процентных ставок на денежном рынке и т. д.).

При обесценении денег потребители увеличивают покупки товаров, для того чтобы оградить себя от падения покупательной способности денег, что ускоряет денежный оборот. При прочих равных условиях ускорение скорости обращения денег равнозначно увеличению денежной массы и является одним из факторов инфляции.

Применяемые кредитными институтами методы покрытия бюджетного дефицита обычно вызывают рост денежной массы в обращении сверх реальных потребностей экономического оборота, обесценение денег.

В условиях нормально развивающейся экономики денежно-кредитное регулирование обеспечивает расширение кредитов и увеличение денежной массы (в обращении и на счетах в банках). Денежно-кредитное регулирование на более короткие периоды предполагает сдерживание инфляции путем определения норм обязательных резервов, учетных ставок по кредитам, установление экономических нормативов для банков, проведение операций с ценными бумагами и валютой.

Все денежные средства – наличные и безналичные – должны иметь кредитную основу. Выдача кредита увеличивает количество денег или денежную массу, погашение кредита уменьшает количество денег (наличных и безналичных), поэтому предоставление ссуд должно осуществляться на макроуровне с учетом действия денежно-кредитных законов.

Стабильный и умеренный рост денежной массы, при соответствующем росте объема производства, обеспечивает постоянство уровня цен. Лишь в этом случае рыночные отношения воздействуют на экономическую систему самым эффективным и выгодным образом.

На инфляцию влияет импортируемая инфляция – это эмиссия национальной валюты сверх потребностей товарооборота при покупке иностранной валюты странами с активным платежным балансом. Внешнеэкономическая составляющая инфляционного процесса, или импортируемая инфляция, имеет два основных канала проникновения в национальную экономику.

Первым источником внешних инфляционных импульсов может быть понижение валютного курса денежной единицы, которое повышает рыночные цены импортируемых потребительских товаров. Что касается ввозимого из-за границы сырья и полуфабрикатов, то их удорожание в национальных деньгах увеличивает стоимость товаров, производимых с их помощью внутри страны, а значит, приводит в действие механизм инфляции издержек.

Второй тип инфляционного воздействия извне – чрезмерное расширение денежной массы (денежного предложения) в результате возникновения крупного и устойчивого активного сальдо платежного баланса по текущим операциям, либо массированного притока капитала. Это приводит в действие инфляцию спроса.

Таким образом, инфляция является многофакторным процессом. Она может возникнуть под действием как денежных факторов (объем денежной массы, импортируемая инфляция, которую вызывают понижение валютного курса денежной единицы, которое повышает рыночные цены импортируемых потребительских товаров, и чрезмерное расширение денежной массы и т.д.), так и неденежных (падение роста производительности труда, снижение объемов производства, монополизм и т.д.)

3. Моделирование и прогнозирование уровня инфляции на примере Украины

На основании выделенных в главе 2 основных факторов влияющих на изменение индекса инфляции проанализируем многофакторную корреляционно-регрессионную модель прогнозирования уровня инфляции на Украине с 2008 по 2012 года.

На мой взгляд, наиболее важными факторами, влияющими на уровень инфляции, являются следующие: валовой внутренний продукт, денежная масса ( ), учетная ставка НБУ, доходы населения, объем привлеченных депозитов и выданных кредитов, золотовалютные резервы НБУ (Таблица 2).

Таблица 1. Факторы, влияющие на индекс инфляции

Год	Индекс инфляции, % (Y)	Денежный агрегат М₃ млн. грн. (X₁ )	ВВП, млн. грн. (X₂ )	Учетная ставка НБУ, % (Х₃ )	Доходы населения, млн. грн. (Х₄ )	Депозиты, млн. гр. (Х₅ )	Кредиты, млн. грн. (Х₆ )	Золотовалютные резервы НБУ, млн. $ (X₇ )	Денежный агрегат М₁ , млн. грн.
1	2	3	4	5	6	7	8	9	10
1998	120,0	15705	102593	60,0	54379	6450	7295	793	10331
1999	119,2	22070	130442	45,0	61865	8270	8855	1094	14094
2000	125,8	32252	170070	27,0	128736	18738	19574	1475	20762
2001	106,1	45755	204190	12,5	157996	25674	28373	3089	29796
2002	99,4	64870	225810	7,0	185073	37715	42035	4417	40281
2003	108,2	95043	267344	7,0	215672	61617	67835	6937	51541
2004	112,3	125801	345113	9,0	274241	82959	88579	9525	67090
2005	110,3	194071	441452	9,5	381404	132745	143418	19395	98573
2006	111,6	261063	544153	8,5	479309	184320	245226	22300	123276
2007	116,6	396156	712945	8,4	625868	279738	426863	32443	181665

Построим и проанализируем матрицу парных коэффициентов корреляции (Таблица 3):

Таблица 2.Матрица парных коэффициентов корреляции


1
-0,056	1
-0,112	0,993	1
0,638	-0,538	-0,614	1
-0,355	0,989	0,997	-0,700	1
-0,271	1,000	0,992	-0,592	0,988	1
-0,245	0,989	0,974	-0,548	0,971	0,991	1
-0,069	0,994	0,991	-0,534	0,977	0,990	0,971	1

Таким образом, можно сделать вывод о том, что наиболее существенный из указанных факторов – это учетная ставка НБУ, при парном коэффициенте корреляции, равном 0,638. Все остальные факторы практически не влияют на индекс инфляции. Так же можно отметить, что между факторами существует взаимосвязь, то есть наблюдается мультиколлинеарность. Парный коэффициент корреляции колеблется в пределах от 0,971 до 0,997.

Согласно основным постулатам экономической теории, важнейшим фактором, обусловливающим обесценивание денег, т. е. инфляцию, является выпуск в обращение денежной массы, необеспеченной произведенными товарами (услугами), либо золотовалютными резервами.

Для определения вышеуказанной обеспеченности денежной массы в работе предложены коэффициенты оборачиваемости эмитированных денег:

1.Коэффициент обеспеченности денежной массы произведенными товарами (услугами):

(1)

Представленный коэффициент показывает, сколько произведенной продукции (услуг) приходится на 1 грн. денежной массы в обращении. Для определения данного показателя, на наш взгляд, целесообразно использовать именно денежный агрегат, учитывающий наиболее мобильные денежные ресурсы в обращении.

2.Коэффициент обеспеченности денежной массы золотовалютными резервами ЦБ:

(2)

Данный коэффициент характеризует величину золотовалютных резервов НБУ в расчете на 1 грн. денежной массы ( ).

Рассчитанные коэффициенты обеспеченности денежной массы по формулам 1, 2 представим в таблице 4.

Таблица 3. Коэффициенты обеспеченности денежной массы

Показатели	Годы
Показатели	1998	1999	2000	2001	2002	2003	2004	2005	2006	2007
Коэффициент обеспеченности денежной массы	9,93	9,26	8,19	6,85	5,61	5,19	5,14	4,48	4,41	3,92
Коэффициент обеспеченности денежной массы	5,05	4,96	4,57	6,75	6,81	7,30	7,57	9,99	8,54	8,19

По данным таблицы 4 можно сделать вывод о том, что значение коэффициента обеспеченности денежной массы произведенными товарами (услугами) за указанный период уменьшилось в 2,5 раза, что не могло не отразиться на уровне инфляции. Такое снижение коэффициента объясняется опережающими темпами роста денежной массы ( ) по сравнению с темпами роста ВВП. Рассчитаем коэффициент опережения темпов роста анализируемых показателей (графы 4, 10 таблицы 2):

(3)

Таким образом можно сделать вывод, что в течении 1998-2007 годов темпы роста денежной массы превышали темпы роста ВВП за этот же период в среднем на 10,9 % ежегодно.

Учитывая динамику изменений предложенных в работе коэффициентов (таблица 4), на мой взгляд, целесообразно оценить их влияние на уровень инфляции, рассматривая их в качестве факторных признаков ( , ), вместе с учетной ставкой НБУ ( ). Для этого построим матрицу парных коэффициентов корреляции (таблица 5).

Таблица 4. Матрица парных коэффициентов корреляции


1
0,532	1
0,638	0,920	1
-0,508	-0,892	-0,734	1

Проанализировав данные таблицы 5 можно сделать вывод, что коэффициент и учетная ставка НБУ связаны с уровнем инфляции прямой заметной связью, а коэффициент связан с уровнем инфляции обратной заметной связью. Поэтому в множественную корреляционно-регрессионную модель уровня инфляции следует включить все три рассматриваемых факторных признака, кроме того, с целью прогнозирования индекса инфляции на последующие годы, необходимо включить в модель фактор времени (t ).

Так, на основе формальных критериев аппроксимации (т. е. ), была выбрана степенная функция с аргументами х₁ , х₂ , х₃ то есть коэффициента обеспеченности денег товарами, учетной ставки НБУ и коэффициента обеспеченности денег золотовалютными резервами (Таблица 6).

Таблица 5. Формальные критерии аппроксимации функций

№ п/п	Название функции
1	2	3	4	5
1	Линейная	4,452	2,656	0,781
2	*Степенная*	*10,51*	*0,384*	*0,894*
3	Экспонента	4,467	0,565	0,781
4	Парабола	3,590	5,964	0,742

Выбранная функция имеет вид:

(4)

На основе коэффициента детерминации (графа 5, таблицы 6) можно сделать вывод, что изменение уровня инфляции на 89,4 % зависит от изменений коэффициента обеспеченности денежной массы произведенными товарами (услугами), учетной ставки НБУ и коэффициента обеспеченности денежной массы золотовалютными резервами НБУ, а остальные 10,6 % – это влияние неучтенных факторов. Так же из выбранной модели видно, что при увеличении коэффициента обеспеченности денежной массы и коэффициента обеспеченности денежной массы на 1 %, индекс инфляции снижается соответственно на 0,225 % и 0,22 %, а увеличение учетной ставки НБУ на 1 %, приводит к повышению индекса инфляции на 0,16 %.

Рассчитанная ошибка аппроксимации, равная 0,894 % (графа 4, таблицы 6), позволяет утверждать, что выбранное уравнение является статистически точным, так как ее значение не превышает 15 %.

Статистическую достоверность уравнения проверим с помощью критерия Фишера (F -критерия). В нашем случае расчетное значение параметра равняется 10,51 (графа 3, таблицы 6). Определим табличное значение критерия:

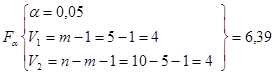(5)

Т. к. (), то с вероятностью 95 % можно утверждать, что выбранное уравнение является статистически достоверным.

Достоверность тесноты связи проверим с помощью t -критерия (критерия Стьюдента). Для этого рассчитаем расчетное значение критерия:

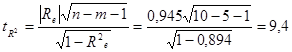(6)

По таблицам распределения Стьюдента определим табличное значение критерия:

(7)

С вероятность 70 % можно утверждать, что множественный коэффициент корреляции в приведенной модели является статистически достоверным, так как ().

Для оценки степени влияния каждого факторного признака на уровень инфляции рассчитаем стандартизированное уравнение регрессии:

(8)

Предварительно для каждого из факторов рассчитаем значения через соотношение между натуральными и стандартизированными коэффициентами регрессии:

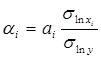(9)

Таким образом, подставляя полученные значения в формулу 8, получим стандартизированное уравнение, которое имеет следующий вид:

Можно судить о том, что наибольшее влияние на индекс инфляции оказывает первый фактор – это коэффициент обеспеченности денежной массы произведенными товарами (услугами), а наименьшее влияние оказывает коэффициент обеспеченности денежной массы золотовалютными резервами НБУ.

Так как наибольший удельный вес влияния на уровень инфляции среди представленных признаков занимает коэффициент обеспеченности денежной массы , то целесообразно определить экстремум функции индекса инфляции от данного фактора:

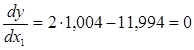
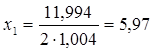
Таким образом (таблица 4), еще начиная с 2002 года, значение коэффициента обеспеченности вышло за пределы допустимых значений, и уже более 5 лет обеспечивает высокий уровень инфляции, который уже не стимулирует развитие экономики, а имеет лишь негативные последствия. Так, уже в 2002 году данный коэффициент составлял 5,61 при допустимом уровне не менее 5,97.

По формальным критериям аппроксимации были определены наиболее оптимальные методы прогноза, с помощью которых были спрогнозированы уровни факторных признаков на 2008-2012 гг. Для прогнозирования значений коэффициента обеспеченности денежной массы произведенными товарами (услугами) была выбрана экспоненциальная функция, уравнение которой имеет следующий вид:

(,, , МНК=1,449).

Учетная ставка НБУ и коэффициент обеспеченности денежной массы золотовалютными резервами НБУ были спрогнозированы с помощью метода ОЛИМП.

Прогнозные значения факторных признаков вместе с рассчитанными доверительными интервалами (ДИ), то есть с нижней (НГ) и верхней (ВГ) границами, соответственно, представим в таблице 7.

Таблица 6. Прогнозные значения факторных признаков

Год	Коэффициент обеспеченности денежной массы , ()			Учетная ставка НБУ, % ( )			Коэффициент обеспеченности денежной массы , ()
	Прогноз	ДИ		Прогноз	ДИ		Прогноз	ДИ
	Прогноз	НГ	ВГ	Прогноз	НГ	ВГ	Прогноз	НГ	ВГ
2008	3,3	0,9	5,7	8,3	6,3	10,2	8,79	7,5	10,1
2009	3,0	0,6	5,4	8,0	5,7	10,4	8,92	7,1	10,8
2010	2,7	0,3	5,1	8,0	5,4	10,4	9,04	6,9	11,1
2011	2,4	0,2	4,8	7,9	5,5	10,5	9,15	7,0	11,3
2012	2,2	-0,2	4,6	7,9	5,6	10,6	9,24	7,1	11,4

Подставив в исходную степенную функцию (формула 4) прогнозные значения факторов, получаем прогноз уровня инфляции на 2008-2012 гг. Предварительно рассчитаем доверительные интервалы прогноза:

(10)

Определим погрешность уравнения регрессии:

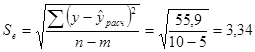(11)

Погрешность параметров уравнения, рассчитанная с помощью таблиц распределения Стьюдента, равняется 1,11 (формула 7).

Таким образом, при сложившихся тенденциях, с вероятностью 70 % можно утверждать, что уровень инфляции в 2008 году будет находиться в пределах от 17,29 % до 24,71 % (Таблица 8):

Таблица 7. Прогнозные значения и доверительные интервалы индекса инфляции на 2008-2012 гг., %

Год	Прогноз	Доверительный интервал
Год	Прогноз	Нижняя граница	Верхняя граница
2008	121	117,29	124,71
2009	122,2	118,39	126,1
2010	125,1	122	128,2
2011	128,9	125,3	132,5
2012	131,6	128,6	134,6

Так как уже имеются данные по реальной инфляции 2008-09 годов на Украине, то проведем сравнения их с прогнозированными данными полученными в данной модели. Индекс инфляции в 2008 году составил 122,3 %, который входит в прогнозный доверительный интервал и очень близок к прогнозному значению (121 %). В 2009 году индекс инфляции на Украине составил 112,3 %, который не входит в полученный доверительный интервал, на 6,09 % меньше нижней границы и на 9,9 % меньше прогнозного значения. По-моему мнению несоответствие прогнозного значения с реальным вызвано происходящими на Украине социально-экономическими событиями, которые напрямую повлияли на индекс инфляции:

· Сокращение ВВП Украины по итогам второго квартала 2009 г. составило 18 % (в годовом исчислении). В условиях отрицательного платежного баланса и значительного бюджетного дефицита продолжается ослабление национальной валюты. Быстро растет внешний долг – госдолг Украины к концу года, по оценке МВФ, достигнет 35,4 % ВВП, а валовой внешний долг 85,4 %.

· В январе-августе 2009г. спад промышленного производства достиг 29,6 % в годовом исчислении. Причины спада – обвальное падение спроса на украинскую продукцию на мировом рынке, устаревшая технологическая база и высокая энергоемкость.

· Реальная заработная плата уменьшилась в первом полугодии более чем на 10 %. В то же время остановился рост безработицы (9,1 % по методологии международной организации труда).

· Стремясь оживить кредитный рынок, Национальный банк Украины последовательно снижает учетную ставку

· Из-за резкого сокращения внутреннего спроса в текущем году снизилась потребительская инфляция, а в августе зафиксирована сезонная дефляция.

Заключение

Инфляция является многофакторным процессом. Она может возникнуть под действием как денежных факторов (объем денежной массы, импортируемая инфляция, которую вызывают понижение валютного курса денежной единицы, которое повышает рыночные цены импортируемых потребительских товаров, и чрезмерное расширение денежной массы и т.д.), так и неденежных (падение роста производительности труда, снижение объемов производства, монополизм и т.д.)

В ходе проведения практического исследования среди множества факторов, влияющих на индекс инфляции, были выбраны наиболее существенные. В частности – учетная ставка НБ. Так же были предложены два показателя – коэффициент обеспеченности денежной массы произведенными товарами (услугами) и коэффициент обеспеченности денежной массы золотовалютными резервами НБ, которые в последствии были включены в степенную модель уровня инфляции, выбранную на основе формальных критериев аппроксимации.

На основании практического примера можно сделать выводы о том, что прогнозные значения индекса инфляции будут повышаться в течение ближайших 5 лет, в частности до 131,6 % уже к 2012 году. Но нужно помнить, что сделанные выводы верны в предположении сохранения макро- и микроэкономических тенденций, при их изменении, использование корреляционно-регрессионной модели неадекватно, это видно из не соответствия реального значения индекса инфляции 2009 года и его прогнозного значения. Такой уровень инфляции, а также последствия мирового финансового кризиса будут иметь крайне негативные последствия для экономики страны – обесценятся сбережения населения, прекратятся долгосрочные инвестиции и реальный экономический рост, девальвирует национальная валюта, ухудшатся показатели государственного бюджета и др.

Такая ситуация требует неотложного вмешательства государственных органов для решения этой проблемы. С учетом существующих реалий необходимо разработать актуальную антиинфляционную политику, которая бы включала политику краткосрочных, среднесрочных и стратегических мер, которые в комплексе могут принести ожидаемые обществом стабилизационные результаты.

Список литературы

1. Прогнозирование и планирование экономики. Учебное пособие. В.И. Борисевич, Г.А. Кандаурова – Мн.: Экоперспектива, 2001 – 380 с.

2. Методы прогнозирования социально-экономических процессов. Учебное пособие. И.В. Антохонова – Улан-Удэ: ВСГТУ, 2004 – 212 с.

3. Эконометрические методы. Дж. Джонстон. - М.: Статистика, 1980 – 444 с.

4. Эконометрика. Учебник. И.И. Елисеевой. – М.: Финансы и статистика, 2002 – 344 с.

5. Введение в экономико-математическое моделирование. Учебное пособие. А.В. Лотов – М.: 1984 – 355 с.

6. Математическое моделирование экономических процессов. Учебное пособие – М.: Экономика, 1990 – 378 с.

7. Инфляция в условиях современного капитализма. Л.Н. Красавина – М.: Финансы, 1997 – 564 с.

8. Деньги. Денежное обращение. Инфляция. В.В. Усов – М.: Банки и биржи, ЮНИТИ, 1999. – 544с.

Скачать архив с текстом документа