Многомерные последовательности Фибоначчи
СОДЕРЖАНИЕ: Государственное учреждение образования Гимназия № 8 г. Витебска МНОГОМЕРНЫЕ последовательности Фибоначчи Витебск, 2009 Содержание Введение, основные понятияГосударственное учреждение образования
Гимназия № 8 г. Витебска
МНОГОМЕРНЫЕ
последовательности Фибоначчи
Витебск, 2009
Содержание
Введение, основные понятия
1. Свойства последовательности
2. Упорядочивание, вычисление элементов последовательности
3. Некоторые зависимости между мнимыми тройками
4. Практическое применение, дополнения
4.1 Решение задачи «Математики играют»
4.2 Фигуры в декартовых системах координат
Заключительная часть
Направления для исследований
Литература
Введение, основные понятия
Широко известна классическая последовательность чисел Фибоначчи, в которой первые два элемента равны единице (F1 =F2 =1), а каждый последующий равен сумме двух предыдущих. (Fi +2 =Fi +1 +Fi .) В данной работе представлена последовательность, схожая по построению с последовательностью Фибоначчи, но состоящая не из чисел, а из троек чисел (Далее будем называть её трёхмерной последовательностью Фибоначчи). Цель данной работы – найти формулы зависимости между её членами, рекуррентные соотношения, общие формулы. Также в работе рассмотрены возможные применения данной последовательности: при решении задачи из турнира юных математиков (г. Минск, 2007 г.), и кроме этого, были рассмотрены фигуры в декартовых системах координат, чьи вершины имеют координаты, равные соответствующим компонентам троек.
Дадим определение основным понятиям.
· Аддитивная тройка – тройка целых чисел (a, b, c), где одно из чисел равно сумме двух других. Натуральной аддитивной тройкой назовём ту, в которой все числа натуральны, мнимой аддитивной тройкой назовём ту, в которой хотя бы одно число неположительное.
· Производная аддитивной тройки первым и вторым способом. Занумеруем переменные циклически. Пусть в некоторый момент i-1, i, i+1 – номера компонент тройки, полученные циклической перестановкой номеров 1, 2, 3, причём такой, что число с номером i равно сумме двух других. Тогда её производная «первым способом» - это тройка чисел, где числа с номерами i, i-1 остаются неизменными, а число с номером i+1 заменяется на сумму двух других. Аналогично, производная вторым способом – это та тройка, где числа с номерами i, i+1 остаются неизменными, а число с номером i-1 заменяется на сумму двух других.
· Производную первым способом от аддитивной тройки T обозначим f(T), а производную вторым способом – g(T).
Например, производные от тройки (1, 2, 3) первым и вторым способом соответственно – это тройки (5, 2, 3) и (1, 4, 3). При этом тройки вида (p+q,p,q) назовём аддитивными тройками 1 рода, тройки вида (p,p+q,q) – аддитивными тройками 2 рода, тройки вида (p,q,p+q) – соответственно аддитивными тройками 3 рода.
· Простейшие тройки – это аддитивные тройки (2,1,1), (1,2,1) и (1,1,2)
· Множество на k-том ходу – это некоторое множество, состоящее из нескольких аддитивных троек. Правила построения этих множеств будут описаны ниже. Каждая аддитивная тройка является либо простейшей тройкой, либо производной от некоторой другой аддитивной тройки.
1. Свойства последовательности
Построим последовательность, и назовём её трёхмерной последовательностью Фибоначчи . Эта последовательность будет состоять из множеств М1 , М2 , … и так далее. Множество М1 состоит всего из одной аддитивной тройки (2,1,1). Далее строим последовательность следующим образом: Если аддитивная тройка Т содержится в Мi , то её производная первым способом содержится в Мi +1 , а производная вторым способом содержится в Мi +2. Кроме этого, множество М2 дополняется простейшей тройкой (1,2,1), а множество М3 – соответственно простейшей тройкой (1,1,2).
Понятно, что при этом аддитивные тройки 1 рода лежат в множествах М1 , М4 , М7 , …, М3 k +1 , …, аддитивные тройки 2 рода соответственно лежат в множествах М2 , М5 , М8 , …, М3 k +2 , …, и, наконец тройки 3 рода – соответственно в множествах М3 , М6 , М9 , …, М3 k , …
Ниже представлено схематическое изображение этой последовательности, в виде таблицы:
Мн-во |
Тройки | |Mi| | |||||||||||
| M1 | 1 | ||||||||||||
| M2 | 2 | ||||||||||||
| M3 | 4 | ||||||||||||
| M4 | 6 | ||||||||||||
| M5 | (8,13,5) | (4,5,1) | (4,7,3) | (5,8,3) | (3,5,2) | 10 | |||||||
| (2,7,5) | (2,5,3) | (3,4,1) | (1,4,3) | (1,3,2) | |||||||||
| … | … | 16 | |||||||||||
Заметим, что начиная с n=3, количество элементов во множестве Mi равняется i-тому числу из последовательности Фибоначчи, умноженному на 2. (|Mi |=2Fi ).
Действительно, каждое множество состоит из производных троек предыдущего множества, и предыдущего за ним. Поэтому его мощность равняется сумме мощностей двух предыдущих множеств. Для n3 |Mi |=|Mi -1 |+|Mi -2 | (Под последовательностью Фибоначчи здесь понимается последовательность Fn , где F1 =F2 =1, Fi +2 =Fi +1 +Fi , i1)
Номер той компоненты тройки, которая равняется сумме двух других, соответствует остатку при делении числа q на 3, где q – номер множества, в котором содержится данная тройка.
Свойства трёхмерной последовательности Фибоначчи
Докажем следующие две теоремы:
1. Все числа аддитивной тройки попарно взаимно просты.
2. Любая аддитивная тройка со взаимно простыми компонентами входит в трёхмерную последовательность Фибоначчи, причём ровно один раз.
Доказательство (Теорема 1). Посчитаем наибольший общий делитель любых двух чисел в такой тройке. По алгоритму Евклида, он равен наибольшему общему делителю в предыдущей аддитивной тройке, из которой была образована данная. Так как все такие тройки, в конечном итоге, образуются из простейших троек, в которых любые два числа взаимно просты, то в любой тройке все числа попарно взаимно просты. Теорема доказана.
Доказательство (Теорема 2). Разобьём теорему на два утверждения. Первое утверждение: «Никакая тройка в последовательности не встретится дважды». Второе утверждение: «Любая аддитивная тройка со взаимно простыми компонентами входит в трёхмерную последовательность Фибоначчи».
Обозначим за ![]() отношение между двумя числами, сумма которых образует третье число аддитивной тройки (для удобства отношения можно брать циклически, например, если сумма стоит на втором месте в тройке, то берётся отношение третьего числа к первому; а если сумма стоит на первом месте, то рассматривается отношение второго числа к третьему). Так как числа аддитивной тройки попарно взаимно просты, то можно считать несократимой дробью. Для конкретной тройки Ma
[b] известен номер множества, в котором она содержится, значит, можно сказать, на каком месте в тройке стоит сумма. Следовательно (так как числа взаимно просты), из несократимой дроби
отношение между двумя числами, сумма которых образует третье число аддитивной тройки (для удобства отношения можно брать циклически, например, если сумма стоит на втором месте в тройке, то берётся отношение третьего числа к первому; а если сумма стоит на первом месте, то рассматривается отношение второго числа к третьему). Так как числа аддитивной тройки попарно взаимно просты, то можно считать несократимой дробью. Для конкретной тройки Ma
[b] известен номер множества, в котором она содержится, значит, можно сказать, на каком месте в тройке стоит сумма. Следовательно (так как числа взаимно просты), из несократимой дроби ![]() можно восстановить исходную тройку. Поэтому далее вместо аддитивных троек мы для удобства доказательства будем писать лишь число . Ясно, что если было выписано число , то в более нижних рядах будут выписаны числа
можно восстановить исходную тройку. Поэтому далее вместо аддитивных троек мы для удобства доказательства будем писать лишь число . Ясно, что если было выписано число , то в более нижних рядах будут выписаны числа ![]() и
и ![]() . Теперь докажем исходные утверждения. Понятно, что производная «первым способом», то есть f() даёт тройку (
. Теперь докажем исходные утверждения. Понятно, что производная «первым способом», то есть f() даёт тройку (![]() ), а вторым способом, то есть g(), даёт тройку (
), а вторым способом, то есть g(), даёт тройку (![]() ). Зная такое число, можно определить (с учётом приведенных неравенств), с помощью какой производной оно было образовано. Действительно, если 1, то она образована с помощью первой производной, если 1, то с помощью второй. Если =1, то эта тройка – простейшая. Итак, для каждой аддитивной тройки мы однозначно восстанавливаем её первообразные вплоть до простейшей тройки. Если бы встретились две одинаковые тройки, то они, с учётом приведенных рассуждений, были бы образованы от одной простейшей, и стояли бы в одном множестве, а значит, совпадали. Поэтому такое невозможно. Первое утверждение доказано. С другой стороны, чтобы доказать второе утверждение, достаточно рассмотреть произвольную дробь
). Зная такое число, можно определить (с учётом приведенных неравенств), с помощью какой производной оно было образовано. Действительно, если 1, то она образована с помощью первой производной, если 1, то с помощью второй. Если =1, то эта тройка – простейшая. Итак, для каждой аддитивной тройки мы однозначно восстанавливаем её первообразные вплоть до простейшей тройки. Если бы встретились две одинаковые тройки, то они, с учётом приведенных рассуждений, были бы образованы от одной простейшей, и стояли бы в одном множестве, а значит, совпадали. Поэтому такое невозможно. Первое утверждение доказано. С другой стороны, чтобы доказать второе утверждение, достаточно рассмотреть произвольную дробь ![]() и показать, что с помощью приведенных выше преобразований можно получить эту дробь из единицы. Это нетрудно сделать, используя алгоритм Евклида. Если дробь больше единицы, отнимем от неё единицу. Если меньше, то разделим единицу на эту дробь. Так как числа в дроби взаимно просты, то бесконечно такие преобразования выполнять нельзя, поэтому рано или поздно мы придём к единице, а значит, такое число (и соответствующая ему аддитивная тройка) будет содержаться в 3-х мерной последовательности Фибоначчи.
и показать, что с помощью приведенных выше преобразований можно получить эту дробь из единицы. Это нетрудно сделать, используя алгоритм Евклида. Если дробь больше единицы, отнимем от неё единицу. Если меньше, то разделим единицу на эту дробь. Так как числа в дроби взаимно просты, то бесконечно такие преобразования выполнять нельзя, поэтому рано или поздно мы придём к единице, а значит, такое число (и соответствующая ему аддитивная тройка) будет содержаться в 3-х мерной последовательности Фибоначчи.
Теорема доказана.
2. Упорядочивание, вычисление элементов последовательности
Упорядочим элементы каждого множества следующим образом:
Для начала, i-тый элемент множества Mk будем обозначать Мk [i].
В первом множестве находится единственная аддитивная тройка: М1 [1]= =(2,1,1).
f(Мa [b]) = Ma +1 [b] (Первая производная от аддитивной тройки Мa [b] лежит в следующем множестве, но индекс аддитивной тройки сохраняется.)
g(Ma [b]) = Ma +2 [b+|Ma +1 |] (Вторая производная от аддитивной тройки лежит в множестве «через одно», индекс увеличивается на количество элементов в множестве Мa +1 .)
Изобразим это схематически (каждая аддитивная тройка обозначена точкой).
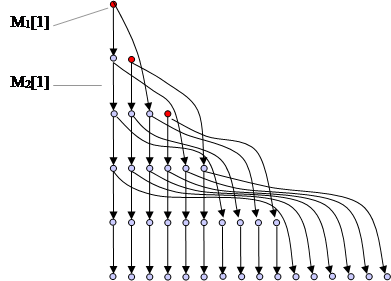 |
Итак, мы занумеровали, то есть упорядочили элементы каждого множества Мi . Определим для всех a и b, для которых определена аддитивная тройка Мa [b], все три её элемента.
Для начала найдём все тройки вида Ma [1] (тройки первого столбца). Вычисляя результаты первых троек, замечаем общую закономерность и вычисляем общий вид.
M1 [1] = (2, 1, 1) = (F3 , F1 , F2 ) |
M3k+1 [1] = (F3k+3 , F3k+1 , F3k+2 ) |
M2 [1] = (2, 3, 1) = (F3 , F4 , F2 ) |
M3k+2 [1] = (F3k+3 , F3k+4 , F3k+2 ) |
M3 [1] = (2, 3, 5) = (F3 , F4 , F5 ) |
M3k [1] = (F3k , F3k+1 , F3k+2 ) |
Заметим, что если требуется вычислить некоторое число из обычной последовательности Фибоначчи, возможно, с изменёнными первыми членами, то для этого идеально подходит характеристический многочлен. Таким образом, все аддитивные тройки первого столбца можно вычислить в общем виде.
3. Некоторые зависимости между мнимыми тройками
Теперь расширим понятие Ma [b]. Определим её для всех целых a. Для этого введём понятие «первообразной».
Первообразной от аддитивной тройки Т1
назовём такую аддитивную тройку Т0
, что производная первым способом от неё равна аддитивной тройке Т1
. При этом стоит отметить, что не каждая первообразная является натуральной тройкой, то есть не все числа в первообразной натуральны. ![]()
Первообразные от троек считаются по следующему правилу:
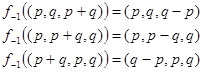
Аналогичным образом можно определить «N раз производную» и «N раз первообразную» - это композиции N подряд идущих функций либо f, либо g, либо f-1. Поместим первообразную от аддитивной тройки Ma [b] во множество Ma -1 ,
то есть f-1 (Ma [b])=Ma -1 [b]. Таким образом, многомерная последовательность Фибоначчи определена Ma [b] для всех целых b.
Теперь полученную 3х-мерную последовательность Фибоначчи можно изобразить так:
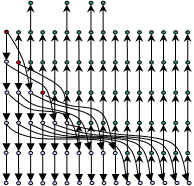
Итак, определены все аддитивные тройки Ma [b], где b – натуральное, a целое. В частности, рассмотрим аддитивные тройки вида M1 [i], то есть тройки, находящиеся в первом ряду.
Каждая такая аддитивная тройка имеет вид (xi +yi , xi , yi ) и определяется двумя числами: xi и yi .
Рассмотрим последовательность Фибоначчи, в которой первые два числа равны соответственно xi и yi , а каждое число, начиная с третьего по-прежнему равняется сумме двух предыдущих. Зная числа xi , yi i-того столбца можно вычислить все аддитивные тройки в этом столбце, по аналогии с первым столбцом.
Итак, имеют место следующие равенства:
| M3k+1 [i]=(F3k+3 , F3k+1 , F3k+2 ) | M1 [i]=(xi +yi , xi , yi ) |
| M3 k +2 [i]=(F3 k +3 , F3 k +4 , F3 k +2 ) | F1 =xi , F2 =yi |
| M3 k [i]=(F3 k , F3 k +1 , F3 k +2 ) | Fn +2 =Fn +1 + Fn |
Понятно, что если мы найдём первую аддитивную тройку некоторого столбца, то сможем вычислить и все остальные тройки этого столбца. Ниже записаны первые тройки столбцов с номерами от 1 до 10.
M1[1]=(2, 1, 1)
M1[2]=(1, 0, 1)
M1[3]=(2, 3, -1)
M1[4]=(1, 1, 0)
M1[5]=(-2, -7, 5)
M1[6]=(-1, 4, 3)
M1[7]=(8, 19, -11)
M1[8]=(5, 12, -7)
M1[9]=(4, 9, -5)
M1[10]=(3, 7, -4)
Ниже изложен алгоритм по нахождению общего члена последовательности. Для начала определим ряд Фибоначчи для всех целых чисел. F- n =(-1)n +1 Fn .
Далее определим формулу для «N раз производной» (эта же формула выполняется для «N раз первообразной»)
Пусть исходная тройка имеет вид:
![]()
Тогда её производные равны:
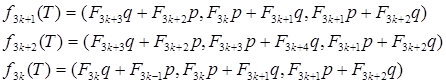
Теперь вычислим все элементы первой строки рекуррентно, но с маленьким числом действий.

Для начала заметим, что каждое число n большее 4 лежит между двумя удвоенными числами Фибоначчи. (2Fi
-1
![]() n
n![]() 2Fi
) Каждому n поставим в соответствие номер i и назовём это «обратной функцией Фибоначчи» для n. Где это используется при решении задачи? Оказывается, такая «обратная функция» от n указывает на номер строки, в которой первый раз для данного столбца встречается натуральная тройка. Действительно, количество элементов каждой строки (кроме первой) равняется удвоенному соответствующему числу Фибоначчи. Назовём такую обратную функцию lF
(N).
2Fi
) Каждому n поставим в соответствие номер i и назовём это «обратной функцией Фибоначчи» для n. Где это используется при решении задачи? Оказывается, такая «обратная функция» от n указывает на номер строки, в которой первый раз для данного столбца встречается натуральная тройка. Действительно, количество элементов каждой строки (кроме первой) равняется удвоенному соответствующему числу Фибоначчи. Назовём такую обратную функцию lF
(N).
Теперь, опускаясь из тройки первого столбца в первую натуральную тройку, и далее поднимаясь по стрелке (так как такая тройка всегда образована с помощью производной «вторым способом»), нетрудно проверить справедливость следующей формулы:
![]()
Например,
![]()
Наряду с общей формулой, для всех натуральных троек верна более простая, рекуррентная, которая следует из определения (эта формула для мнимых троек, вообще говоря, не выполняется):
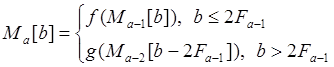
Некоторые зависимости между мнимыми тройками
Для начала выпишем таблицу, содержащую некоторые тройки не в схематическом, а в непосредственном виде. (см. приложение)
Если брать производные вторым способом от мнимых троек, можно заметить следующие закономерности (для некоторых троек), например:
f-2 (g(T))=g-1 (f2 (T))
g(f-3 (g(T)))=-f(g(f(T)))
Их можно доказать, используя определение производных и первообразных. Докажем утверждение для тройки 1 рода (аналогичное утверждение для остальных получается циклическим сдвигом компонент)
1. f-2 (g(T))=g-1 (f2 (T))
(p + q , p, q) -(f)-(p+q, p +2 q , q) -(f)-(p+q, p+2q, 2 p +3 q )-(g-1 )-(p + q , p+2q, -q)
(p + q , p, q) -(g)-(p+q, p, 2 p + q ) -(f-1 )-(p+q, p , -q) - (f-1 )- (p + q , p+2q, -q)
Так как конечные результаты преобразований верны для любых чисел p, q, то утверждение верно для любых троек Т. Аналогично доказывается второе утверждение.
2.g(f-3 (g(T)))=-f(g(f(T)))
(p + q , p, q) -(g)-(p+q, p, 2p+q) - (f-1 ) – (p+q, p, -q) - (f-1 ) - (p+q, p+2q, -q) - (f-1 ) -
- (-p-3q, p+2q, -q) -(g) - (-p-3q, -p-4q, -q) = -(p+3q, p+4q, q)
(p+1,p,q)- (f) - (p+q, p+2q, q) - (g) - (p+3q, p+2q, q) - (f) - (p+3q, p+4q, q)
Далее исследуем условия, необходимые и достаточные для существования аддитивной тройки в трёхмерной последовательности Фибоначчи.
Лемма. Если тройка (a,b,c) находится в трёхмерной последовательности Фибоначчи, то хотя бы одно из чисел a,b,c положительно.
Доказательство. Допустим, что в данной тройке все компоненты отрицательны. Ясно, что если тройка содержится в последовательности, то строя производные от неё (первым способом), мы рано или поздно получим тройку со всеми натуральными компонентами. Но если брать производные от тройки с неположительными компонентами, то будут получаться только тройки с неположительными компонентами. Противоречие. Лемма доказана.
Примечание. Все приведенные ниже теоремы верны для циклического сдвига компонент троек.
Теорема
Пусть p,q – натуральные взаимно простые числа. Тогда верны следующие утверждения.
а) тройка (p+q, p, -q)=T всегда находится в трёхмерной последовательности Фибоначчи.
б) тройка (p+q, -p, q)=T находится в последовательности тогда и только тогда, когда ![]() (
(![]() - золотое сечение,
- золотое сечение, 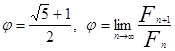 )
)
в) тройка (-p-q, p, -q)=T находится в последовательности тогда и только тогда, когда ![]()
г) тройка (-p-q, -p, q)=Tне находится в трёхмерной последовательности Фибоначчи.
Доказательство.
а) Возьмём производную от тройки, первым способом. Получим:
f(p+q, p, -q)=(p+q, p, 2p+q). То есть раз мы получили натуральную тройку, то исходная тройка действительно содержится в исходной последовательности.
г) Аналогично, возьмём производную. f(-p-q, -p, q)=(-p-q, -p, -2p-q). Получена тройка с отрицательными компонентами, а по лемме, приведенной в начале главы, такой тройки не содержится в последовательности, значит, исходная тройка в последовательности также не содержится.
в) Строя последовательно производные, получаем тройки, каждая компонента которых имеет вид Fn
q-Fn
+1
p. Так как в конечном итоге каждая компонента должна стать больше нуля, то неравенство Fn
q-Fn
+1
p0 должно выполняться для всех nM для некоторого M. При n стремящемся к бесконечности получаем ![]() , или
, или ![]()
б) Аналогично получаем (умножая все числа в пункте в. на минус один), что каждая компонента имеет вид -Fn
q+Fn
+1
p0, и ![]() .
.
Как следствие, из троек в условии пунктов б) и в) существует ровно одна.
Исследуем содержимое множеств, используемых при построении. Через Sобозначим множество троек, содержащихся в трёхмерной последовательности Фибоначчи. Sg – это множество {g(T) | TS}. Множество SZ будет обозначать множество всевозможных троек с попарно взаимно простыми целыми компонентами.
Можно предположить, что выполняется следующее утверждение:
Sg S=Sz
Также можно выдвинуть следующую гипотезу: если бы мнимая часть последовательности S строилась при помощи применения первообразной вторым способом, а не первым, то такая последовательность S0 не совпадала бы с исходной последовательностью S.
4. Практическое применение
4.1 Решение задачи «Математики играют»
Задача. У трёх математиков написаны на головах натуральные числа, причём одно из них равно сумме двух других. Каждый математик видит два других числа, но не видит своё. Каждого математика спрашивают (по кругу), знает ли он своё число. Докажите, что через некоторое время кто-то из математиков угадает число, написанное у него на лбу, причём это будет тот математик, у которого написана сумма двух других чисел.
Решение. Рассмотрим трёхмерную последовательность, где все числа умножены на одну и ту же натуральную константу a. Назовём ответ каждого математика ходом; числа первого, второго и третьего математика поместим в упорядоченную тройку в соответственном порядке. Нетрудно показать, что множество Mi содержит все возможные тройки на i-том ходу. Докажем это при помощи математической индукции. Для начала, понятно, что если тройка имеет вид (2a,a,a), то математик, видя перед собой два равных числа, определяет, что у него на голове написана не сумма чисел, а их разность. Аналогичное верно для троек (a,2a,a), (a, a, 2a). Теперь положим, что для первых k чисел доказано, что если тройка чисел (делённая на НОД чисел) находится в множестве Mk , то на k-том ходу математик, у которого на голове написана сумма, угадает своё число. Теперь рассмотрим тройку, содержащуюся в множестве Mk +1 . Математик с суммой на голове (на k+1 ходу должен отвечать именно он) может рассуждать следующим образом: «Допустим, у меня на голове написана разность. Тогда я могу однозначно определить тройку чисел на наших головах. Но в этом случае ещё на предыдущем ходу математик, стоящий передо мной, угадал бы число, написанное на его голове. Следовательно, на моей голове написана не сумма, а разность». Так как было показано, что все возможные тройки содержатся в этой последовательности, то рано или поздно кто-то из математиков отгадает своё число. Более того, так как на 3k+q-том ходу отвечает q-тый математик, и по свойству последовательности, на q-том месте написана сумма двух других чисел, то угадает своё число именно тот математик, у которого на лбу написана сумма. Итак, задача доказана.
Сами по себе интересны некоторые пункты этой задачи.
· Можем ли мы, то есть «наблюдатели», зная ответ математика, угадавшего своё число, и количество ходов перед правильным ответом, определить все остальные числа?
Посмотрим, когда это возможно. Понятно, что каждая аддитивная тройка содержится в одном из множеств Mi, номер которого легко определяется из количества ходов. От нас требуется показать, что из всех аддитивных троек данного множества можно выбрать всего одну, удовлетворяющую условиям. Для начала, обозначим отношение числа, равного сумме, к ответу математика, через некоторое число p. Найдём его для каждой тройки в отдельности. Ясно, что числа на головах математиков получаются домножением всех чисел тройки на этот множитель. Условием для единственности решения является тот факт, что существует единственная тройка, в которой все три числа целые.
· Предположим, что на головах у математиков написаны произвольные целые числа (но не обязательно одно из чисел равно сумме двух других), но математики играют по тем же правилам, то есть считают, что у одного из них всё же на голове написана сумма. Самое примечательное то, что в конце концов найдётся математик, который будет считать, что отгадал своё число.
Для того, чтобы найти это количество ходов, совершим такое преобразование. Ясно, что всем тройкам в трёхмерной последовательности Фибоначчи можно поставить в соответствие некоторое рациональное положительное число (Причём это соответствие будет взаимно однозначным. Этот факт доказывался в начале работы после введения основных понятий, в доказательстве двух теорем). Если одно из таких чисел будет равняться одному из отношений чисел, записанных на головах математиков, и это число будет стоять в соответствующем множестве (номер должен иметь соответствующую кратность трём), то соответствующий математик будет утверждать, что отгадал своё число.
· Числа на головах у математиков не натуральные, а целые. В этом случае, однако, все возможных тройки ограничиваются тремя частными случаями.
· Математиков не четверо, а больше. В этом случае строится по аналогии 4х-мерная, 5-мерная, и т.д. последовательность Фибоначчи. Решение задачи почти аналогично.
4.2 Фигуры в декартовых системах координат, с вершинами в координатах, равных числам тройки
Рассмотрим фигуру в трёхмерном пространстве (возможно, это многогранник, возможно и фигура, все точки которой лежат в одной плоскости), координаты точек которой являются некоторыми тройками из 3х-мерной последовательности Фибоначчи. Исследуем для начала, вид этой фигуры в зависимости от выбранных троек.
· Тройки выбираются таким образом, что сумма чисел всегда стоит на одном и том же месте. Такие тройки или лежат в одном множестве Mi , или лежат, в множествах, чьи индексы различаются на число, кратное трём. Тогда все такие тройки лежат в одной плоскости. Действительно, пусть числа тройки обозначают, соответственно, координаты x, y, z точки, и выполняется условие x+y=z. Но широко известно, что уравнение плоскости имеет вид Ax+By+Cz=0, то есть точка с координатами (x, y, z) удовлетворяет этому условию и лежит в некоторой плоскости (одной и той же для всех таких троек (x,y,z) ). Также, если требуется, чтобы точки не лежали в одной плоскости, нужно следить за тем, чтобы ни одна из координат не была одинаковой во всех выбранных точках, иначе фигура будет лежать полностью в плоскости, перпендикулярной одному из единичных векторов.
· Итак, показано, что вершины многогранника лежат в одной из трёх плоскостей. Например, взяв четыре точки так, чтобы они не лежали в одной плоскости, мы получим тетраэдр. Теперь, зная формулы объёма через координаты точек, нетрудно его (объём) найти.
· Также можно рассматривать тройки точек и считать площади полученных треугольников, если точки не лежат на одной прямой. Для этого проецируем плоскость, содержащую эти точки, на плоскость, определяемую двумя базовыми векторами (например, плоскость Oxy, если плоскость, содержащая данные три точки, не перпендикулярна этой плоскости). А площадь спроецированного в двухмерное декартово пространство треугольника нетрудно посчитать.
Направления для исследований
· Рассмотреть другие способы построения последовательности. К примеру, рассматривать в качестве простейших троек не (2, 1, 1) и её перестановки, а некоторые другие тройки.
· Исследовать зависимости между мнимыми тройками. Также исследовать зависимости между натуральными тройками, к примеру, узнать какие тройки получаются друг из друга перестановкой элементов. Зная числа тройки, определить её положение в последовательности.
· Рассмотреть многомерные последовательности Фибоначчи, состоящие из четвёрок, пятёрок, групп из n элементов.
· Исследовать свойства последовательности, в которой n-ки строятся по следующему правилу: t=ax+by+…+cz, где t – образовываемое число, x, y, …, z –
(n-1) чисел n-ки, a, b, …,c – некоторые действительные коэффициенты.
Литература
1. Воробьёв Н.Н. Числа Фибоначчи. Москва, «Наука», 1969, 112 стр.
2. Задача «Математики играют» IX республиканского турнира юных математиков (Минск, 2007)
2. Тригг Ч. Задачи с изюминкой. Москва, «Мир», 1975, 302 стр. (задачи №№ 97, 209)