Моделювання розробки та прийняття рішень
СОДЕРЖАНИЕ: ВИКОРИСТАННЯ МЕТОДІВ МАТЕМАТИЧНОГО ПРОГРАМУВАННЯ ПРИ ПРИЙНЯТТІ РІШЕНЬ Зміст Поняття моделі та моделювання Формування вимог і адекватність моделейМОДЕЛЮВАННЯ РОЗРОБКИ ТА ПРИЙНЯТТЯ РІШЕНЬ .
ВИКОРИСТАННЯ МЕТОДІВ МАТЕМАТИЧНОГО ПРОГРАМУВАННЯ ПРИ ПРИЙНЯТТІ РІШЕНЬ
Зміст
1. Поняття моделі та моделювання
2. Формування вимог і адекватність моделей
3. Порядок розробки та використання моделей
4. Класифікація моделей прийняття управлінських рішень
5. Поняття програми, програмованих та непрограмованих рішень
6. Моделі лінійного та нелінійного програмування
7. Моделі динамічного програмування
8. Стохастичне програмування
1. Поняття моделі та моделювання
Усяка цілеспрямована діяльність, у тому числі розробка і прийняття рішень повязані з моделюванням.
Моделюванням називається створення деякого образу обєкта-оригіналу, названого моделлю, що у визначених умовах може заміняти сам обєкт-оригінал, відтворюючи цікавлячі дослідника властивості і характеристики оригіналу й одночасно забезпечуючи наочність, видимість, приступність іспиту, легкість оперування й інші переваги. З визначення випливає, що модель має цільовий характер, тобто вона відображає не сам по собі обєкт-оригінал, а формується, виходячи з поставленої мети відображення цілком конкретних властивостей обєкта моделювання.
Використання моделей дозволяє приймати рішення, при обґрунтуванні яких враховуються всі фактори і альтернативи, що виникають у складних умовах виробничо-господарської діяльності. Тому моделювання розглядається як найефективніший спосіб оптимізації управлінських рішень.
Модель – це відображення в схемі, формулі, взірці тощо характерних ознак об’єкту, який досліджується. Вона є спрощеною конкретною життєвою (управлінською) ситуацією, іншими словами в моделях певним чином відображаються реальні події, обставини тощо.
Необхідність застосування моделей пояснюється наступними причинами:
· складністю реального світу, виробничо-господарської діяльності;
· наявністю багатофакторних залежностей у процесі розв’язання управлінських завдань;
· необхідністю експериментальної перевірки альтернативних управлінських рішень;
· доцільністю орієнтувати управління на майбутнє.
Моделювання направлене на синтез результатів аналітичного пізнання, внаслідок чого описуються загальні закони і закономірності, стабільні властивості елементів і звязків у процесі функціонування або розвитку досліджуваного явища. Моделювання є основною і неодмінною умовою розвитку аналізу.
Модельний опис закономірностей змісту робіт по окремих етапах процесу ухвалення рішень, а також звязків між даними етапами є важливою передумовою подальшого розвитку аналізу господарської діяльності. З другого боку, результати аналізу дозволяють удосконалювати розробку моделей і наблизити їх до реальної ситуації управління господарською діяльністю.
Моделі ухвалення рішень підтримують у першу чергу кількісний аналіз господарських процесів. Моделі дозволяють легше пройти етапи рутинного аналізу – аж до їх автоматизації. Якісний аналіз просувається углиб і вшир, залишаючи пізнані області процесу для модельних описів.
Модель ухвалення рішень є формалізованою частиною рішення управлінської задачі. Одержане на її основі рішення оптимальне лише з погляду формалізованих умов задачі. Субєкт управління доповнює одержане «модельне рішення» необхідним якісним аналізом, враховує свій досвід та інтуїцію і формулює рішення.
Моделі «навчають» враховувати всі формалізовані умови керованого процесу. Творчістю кожного конкретного керівника є облік всієї решти (специфічних з погляду моделі) умов рішення управлінської задачі.
Так само як моделі ухвалення рішень не знижують значущості інтуїції керівника, вони при правильному застосуванні сприяють розвитку ініціативи працівників, покликаних виконувати дані рішення. Модельне рішення враховує всі чинники, відомі керівнику у момент ухвалення рішення, і примушує виконавців повністю використовувати ці чинники. Але в процесі реалізації ухваленого рішення часто виявляються нові можливості і шляхи застосування конкретних умов. Використовування цих прихованих резервів залежить не від моделі, а від дієвості системи стимулювання всього господарського механізму. Моделі прийняття рішень можуть бути основою розробки обґрунтованих систем стимулювання розвитку ініціативи працівників.
2. Формування вимог і адекватність моделей
Багато непорозумінь, а також «розчарування» в результатах застосування моделей виникають через використовування не відповідної для даної задачі моделі або застосування моделі для вирішення задачі, яка не відповідає її можливостям. Адекватність управлінських моделей необхідно оцінювати принаймні з трьох точок зору (рис. 1):
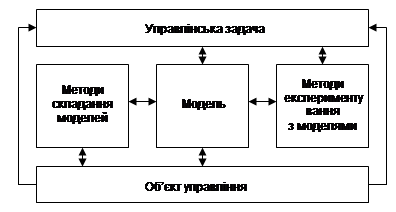
Рисунок 1 – Формування вимог і адекватності моделей
· за відповідністю структурі і властивостям обєкта управління (керованого процесу);
· за відповідністю властивостям і можливостям методів складання даних моделей і експериментування з ними;
· за відповідністю вимогам вирішуваної управлінської задачі.
При складанні моделей необхідно, поза сумнівом, враховувати вживаність моделей із субєктивної точки зору.
3. Порядок розробки та використання моделей
Світова практика виробила певний порядок розробки моделей. Найдоцільніше застосовувати такий процес їх побудови:
· постановка завдання;
· формування моделі;
· перевірка моделі на достовірність;
· використання моделі;
· відновлення моделі.
Постановка задачі. Перший і найважливіший етап побудови моделі, здатний забезпечити правильне рішення управлінської проблеми, полягає в постановці задачі. Правильне використовування математики або компютера не принесе ніякої користі, якщо саму проблему не буде точно діагностовано.
Побудова моделі. Після правильної постановки задачі наступним етапом процесу передбачена побудова моделі. Розробник повинен визначити головну мету моделі, які вихідні нормативи або інформацію передбачається одержати, використовуючи модель, щоб допомогти керівництву вирішити проблему, що стоїть перед ним. На додаток до встановлення головних цілей, фахівець з науки управління повинен визначити – яка інформація потрібна для побудови моделі, що задовольняє цим цілям і видає на виході потрібні відомості.
Перевірка моделі на достовірність. Після побудови моделі її слід перевірити на достовірність. Один з аспектів перевірки полягає у визначенні ступеня відповідності моделі реальному світу. Фахівець з науки управління повинен встановити – чи всі істотні компоненти реальної ситуації вбудовані в модель. Це, звичайно, може виявитися непростою справою, якщо задача складна. Перевірка багатьох моделей управління показала, що вони недосконалі, оскільки не охоплюють всіх релевантних змінних. Природно, чим краще модель відображає реальний світ, тим вище її потенціал як засобу надання допомоги керівнику в прийнятті хорошого рішення, якщо припустити, що модель не дуже складна у використовуванні.
Другий аспект перевірки моделі повязаний зі встановленням ступеня, в якому інформація, одержувана з її допомогою, дійсно допомагає керівництву співволодіти з проблемою.
Використання моделі. Після перевірки на достовірність модель готова до використовування. Якщо моделі науки управління створюються фахівцями штабних служб (а так звично і буває), лінійні керівники, для яких вони призначені, повинні брати участь у постановці задачі і встановленні вимог за інформацією, одержуваною з моделі. Згідно дослідженням, коли це має місце, застосування моделей збільшується на 50%. Крім того, таких керівників слід навчити використовувати моделі, пояснивши серед іншого, як модель функціонує, які її потенційні можливості і обмеження.
Оновлення моделі. Навіть якщо використання моделі виявилося успішним, майже напевно вона зажадає оновлення. Керівництво може знайти, що форма вихідних даних не ясна або бажані додаткові дані. Якщо цілі організації змінюються таким чином, що це впливає на критерії прийняття рішень, модель необхідно відповідним чином модифікувати. Аналогічним чином, зміна в зовнішньому оточенні – наприклад, поява нових споживачів, постачальників або технології – може знецінити допущення і початкову інформацію, на яких ґрунтувалася модель при побудові.
4. Класифікація моделей прийняття управлінських рішень
Перш ніж розглядати широко використовувані сучасними організаціями моделі і задачі, для вирішення яких вони найбільш придатні, необхідно коротко описати три базові типи моделей. Йдеться про фізичні, аналогові і математичні моделі.
Відрізняються такі моделі:
· фізичні. Вони відображають збільшення або зменшення описання об’єкта;
· аналогові. Ці моделі ведуть себе так як реальні об’єкти, але зовнішньо вони не схожі на них;
· математичні (символічні). Для опису властивостей або характеристик об’єкту використовують символи.
Відповідно до того, що мета моделювання в загальному випадку може бути теоретичною і практичною, моделі також розділяються на два види:
· пізнавальні,
· прагматичні.
Пізнавальні моделі є формою організації і представлення знань, засобом зєднання нових знань з наявними. Тому при виявленні розбіжностей між моделлю і реальністю стає завдання усунення цієї розбіжності за допомогою зміни моделі.
Прагматичні моделі є засобом керування, організації практичних дій, способом представлення зразково правильних дій, тобто еталонів чи їхніх результатів. Фактично вони є робочим представленням цілей.
Призначення прагматичних моделей полягає в тому, щоб, при виявленні розбіжностей між моделлю і реальністю, розробити способи і засоби для зміни реальності так, щоб наблизити реальність до моделі. Можна сказати, що прагматичні моделі як би відіграють роль деякого стандарту чи зразка, під яким підбудовується як сама діяльність, так і її результат.
Прикладами прагматичних моделей можуть бути плани і програми дій, статути організацій і кодекси законів, нормативна база, технологічні схеми різних організаційних операцій, алгоритми, робочі креслення і шаблони, параметри добору і технологічні допуски і т.д.
Як всі засоби і методи, моделі науки управління можуть призвести до помилок. Ефективність моделі може бути понижена дією ряду потенційних погрішностей. Щонайчастіше зустрічаються – недостовірні початкові допущення, обмежені можливості отримання потрібної інформації, страхи користувача, слабке використовування на практиці, надмірно висока вартість.
Недостовірні початкові допущення. Будь-яка модель спирається на деякі початкові допущення або передумови. Це можуть бути передумови, що піддаються оцінці, наприклад, що витрати на робочу силу в наступні шість місяців складуть 100 тисяч гривень. Такі припущення можна обєктивно перевірити і підрахувати. Вірогідність того, що вони точні, буде висока. Деякі передумови не піддаються оцінці і не можуть бути обєктивно перевірені. Припущення про зростання збуту наступного року на 10% — приклад допущення, непіддатливого перевірці. Ніхто не знає напевно, чи відбудеться це дійсно. Оскільки такі передумови є основою моделі, точність останньої залежить від точності передумов. Модель не можна використовувати для прогнозування, наприклад, потреби в запасах, якщо неточні прогнози збуту на майбутній період.
Інформаційні обмеження. Основна причина невірогідності передумов і інших утруднень – це обмежені можливості в отриманні потрібної інформації, які впливають і на побудову, і на використовування моделей. Точність моделі визначається точністю інформації з проблеми. Якщо ситуація виключно складна, фахівець з науки управління може бути не в змозі одержати інформацію по всіх релевантних чинниках або вбудувати її в модель. Якщо зовнішнє середовище рухоме, інформацію про неї слід обновляти швидко, але це може бути непрактичним.
Побудова моделі найбільш скрутна в умовах невизначеності. Коли необхідна інформація настільки невизначена, що її важко одержати, виходячи з критерію обєктивності, керівнику, можливо, краще покластися на свій досвід, здібність до думки, інтуїцію і допомогу консультантів.
Страх користувачів. Модель не можна вважати ефективною, якщо нею не користуються. Основна причина невикористовування моделі полягає у тому, що керівники, яким вона призначена, можуть не цілком розуміти одержувані за допомогою моделі результати і тому бояться її застосовувати.
Слабке використовування на практиці. Згідно ряду досліджень рівень методів моделювання в рамках науки управління перевершує рівень використовування моделей. Як наголошувалося вище, одна з причин такої ситуації – страх. Інші причини – це брак знань і опір змінам. Дана проблема підкріплює бажаність того, щоб на стадії побудови моделі штабні фахівці привертали до цієї справи користувачів. Коли люди мають нагоду обговорити і краще зрозуміти питання, метод або передбачувану зміну, їх опір звичайно знижується.
Надмірна вартість. Вигоди від використовування моделі, як і інших методів управління, повинні з лишком виправдовувати її вартість. При встановленні витрат на моделювання керівництву слід враховувати витрати часу керівників вищого і нижчого рівнів на побудову моделі і збір інформації, витрати і час на навчання, вартість обробки і зберігання інформації.
5. Поняття програми, програмованих та непрограмованих рішень
Програмовані рішення – це ті, що повторюються багатократно і мають напрацьовані правила й процедури прийняття.
Непрограмовані рішення – це ті, що виниклу проблему мають вирішувати вперше, отже, всі етапи підготовки рішення треба розробляти спеціально.
Програма - це деталізована послідовність дій, що має деяку мету або завдання і відповідає на реакцію системи та зовнішнього середовища.
Відповідно, програмовані рішення - це гранично деталізована послідовність дій в суворо певних ситуаціях.
Переваги такого підходу очевидні: знижується вірогідність помилки, зменшується час на ухвалення рішення, з виконавця знімається відповідальність.
Проте зрозуміло, що подібний точний алгоритм годиться лише для суворо певної ситуації. Отже, її невірна ідентифікація може призвести до великих втрат. Крім того, в деяких ситуаціях, з часом така схема може стати неефективною або навіть помилковою. Крім всього іншого жорстка регламентація діяльності робить роботу виконавців нецікавою, позбавляє їх ініціативи і знижує увагу. Як правило, чим вищий рівень управління, на якому приймається рішення, і чим більше їх важливість, тим менше частка програмованих рішень.
Непрограмовані рішення використовуються в якісно нових, нестандартних, складних ситуаціях, повязаних з дією невідомих чинників.
6. Моделі лінійного та нелінійного програмування
Моделі лінійного програмування застосовують для знаходження оптимального рішення в ситуації розподілу дефіцитних ресурсів за наявності конкуруючих потреб. Наприклад, за допомогою моделі лінійного програмування керівник виробництвом може визначити оптимальну виробничу програму, тобто розрахувати, яку кількість виробів кожного найменування слід проводити для отримання найбільшого прибутку при відомих обємах матеріалів і деталей, фонді часу роботи устаткування і рентабельності кожного типу виробу. Велика частина розроблених для практичного застосування оптимізаційних моделей зводиться до завдань лінійного програмування.
Максимізуюча (мінімізуюча) функція являє собою прийнятий критерій ефективності вирішення завдань, що відповідає поставленій меті, та називається цільовою функцією.
Обмеження характеризують наявні можливості вирішеня завдання.
Суть розвязання завдань лінійного програмування полягає в знаходженні умов, що спрямовують цільову функцію в мінімум чи максимум.
Рішення, що задовольняє умови завдання і відповідає поставленій меті, називається оптимальним планом.
Якщо кількість змінних системи обмежень і цільової функції в математичній моделі завдання лінійного програмування дорівнює двом або трьом, то таке завдання можна вирішити графічно чи аналітично. При більшій кількості змінних завдання вирішують, як правило, аналітичним шляхом.
З урахуванням характеру аналізованих операцій і форм залежності чинників, що склалися, можуть застосовуватися і моделі інших типів: при нелінійних формах залежності результату операції від основних чинників – моделі нелінійного програмування; при необхідності включення в аналіз чинника часу – моделі динамічного програмування; при імовірнісному впливі чинників на результат операції – моделі математичної статистики (кореляційно-регресійний аналіз).
Умови завдання подаються за допомогою системи лінійних рівнянь чи нерівностей, що виражають обмеження, які накладаються на використання наявних ресурсів:
 , (1)
, (1)
де хj – шукані величини, що містять розвязання поставленого завдання;
аij та bi – відомі постійні величини, що характеризують умови завдання.
Цільова функція (лінійна форма) надається у вигляді:
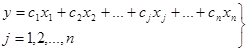 , (2)
, (2)
де сj — постійні коефіцієнти (коефіцієнти вартості).
Умови завдання (обмеження) можуть бути надані також у вигляді нерівностей.
Геометрична інтерпретація завдання лінійного програмування можлива лише при наявності двох незалежних змінних. При трьох змінних наочне уявлення істотно ускладнюється, так як у цьому випадку має місце деякий випуклий багатогранник в трьохвимірному просторі, що відповідає обєму допустимих планів.
При кількості змінних більше трьох завдання втрачає геометричну наочність, так як важко уявити собі, наприклад, чотирьохвимірний простір. Проте ідея одержання рішення, розглянутого вище, зберігає зміст і для випадку багатовимірного простору.
На основі такої ідеї створений і розроблений один з основних методів вирішення завдань лінійного програмування — так званий симплекс-метод.
Симплекс-метод – алгебраїчна форма вирішення завдання лінійного програмування. При обґрунтуванні симплекс-методу звертаються до двохвимірного випадку, що дозволяє досить просто перейти від геометричного уявлення до його алгебраїчної аналогії.
У моделях нелінійного програмування цільова функція чи хоча б одне з обмежень нелінійні (тобто на графіках зображуються непрямими — кривими лініями).
Умови завдання надаються за допомогою системи нелінійних рівнянь чи нерівностей, що виражають обмеження, накладені на використання наявних ресурсів:
 , (3)
, (3)
де Z1 , Z2 , … Zm - відповідні функції, що характеризують умови розвязання поставленого завдання (обмеження);
хi – шуканівеличини, що містять вирішення даного завдання.
Цільова функція подається у вигляді
![]() .(4)
.(4)
Причому, в крайньому разі, одна із функцій у, Z1 , Z2 … нелінійна.
Методами нелінійного програмування вирішуються завдання розподілу неоднорідних ресурсів.
7. Моделі динамічного програмування
Динамічне програмування (динамічне планування) являє собою математичний метод оптимізації рішень, спеціально пристосований до так званих «багатоступеневих» (чи «багатоетапних») операцій.
Сутність вирішення завдань динамічного програмування полягає в наступному:
· оптимізація проводиться методом послідовних наближень (ітерацій) у два кола; спочатку від останньогоступеня операції до першого, а потім, навпаки, - відпершого до останнього ступеня;
· на першому колі, йдучи від наступних ступенів до попередніх, знаходиться так зване умовне оптимальне управління; умовне оптимальне управління вибирається таким, щоб всі попередні ступені забезпечували максимальну ефективність наступного ступеня. Інакше кажучи, накожному кроці наявне таке управління, яке забезпечує оптимальне продовження операції. Цей принцип вибору керування називається принципом оптимальності;
· так триває до першого кроку, але оскільки перший крок не має попереднього, то одержане для нього умовне оптимальне управління втрачає свій умовний характер істає просто оптимальним управлінням, яке ми шукаємо;
· друге коло оптимізації починається з першого кроку, для якого оптимальне управління відоме.
Ефективність управління W(U) залежить від всієї сукупності керувань на кожному кроці операції
W = W(U) = W(U1 , U2 ,… ,Um ). (5)
Управління, при якому показник W досягає максимуму, називається оптимальним управлінням. Оптимальне управління є багатоступеневим процесом і складається із сукупності оптимальних ступеневих керувань
U = (U1 , U2 ,… ,Um ). (6)
Маючи для всіх кроків після нього умовні оптимальні управління, ми знаємо, що необхідно робити на кожному наступному кроці. Це дає нам можливість послідовно переходити від умовних до оптимальних управлінь для всіх наступних кроків, що забезпечує оптимальність операції в цілому.
8. Стохастичне програмування
Стохастичне програмування являє собою сукупність методів планування з вирішення оптимізаційних завдань із врахуванням можливішого (стохастичного) проходження процесів. При цьому під можливішими (стохастичними) чи випадковими процесами розуміють процеси зміни в часі стану якого-небудь елементу системи у відповідності з ймовірними закономірностями.
Завдання лінійного і деяких інших видів програмування стають завданнями стохастичного програмування, якщо параметри цільової функції чи системи обмежень (чи ті й інші) розглядаються як випадкові величини. До таких раніше розглянутих завдань можна віднести проблеми оптимального розподілу ресурсів, транспортне завдання, завдання управління запасами і т.п. Вирішення подібних завдань у стохастичній постановці будуть точніше і коректніше відображати економічний характер процесів, що відбуваються, підвищувати надійність досягнення поставленої мети виробництва.
При вирішенні завдань у стохастичній постановці зазвичай використовують два підходи.
Перший підхід, як більш простий, полягає в знаходженні середнього значення всіх даних випадкових параметрів і зводиться до завдань відповідного раніше розглянутого програмування. Такий підхід, звичайно, не завжди може виявитися ефективним. Це відбувається тому, що при деяких параметрах (випадкових величинах) може бути прийняте рішення зовсім далеке від оптимального через синергетичні явища чи може призвести до ускладнень (навіть відсутності) бажаного рішення поставленого завдання.
Сутність другого підходу полягає в багатоступеневому, поетапному приближенні до бажаного результату. Так, наприклад, на першому етапі встановлюється попередній оптимальний план при вирішенні детермінованого завдання на основі максимізації чи мінімізації цільової функції. Потім на другому ступені цей план коректується у відповідності з реально встановленими статистичними показниками і параметрами.