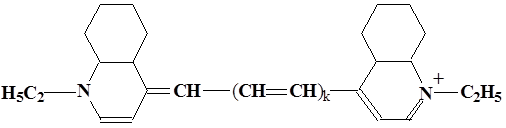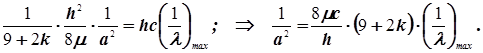Молекулярные спектры
СОДЕРЖАНИЕ: Часть1. Общие характеристики спектров. Часть2. Электронные спектры поглощения молекул. Часть3. Колебательные спектры поглощения молекул. Часть 1. Общие характеристики спектров. Теоретический минимум.“Молекулярные спектры”
Часть1. Общие характеристики спектров.
Часть2. Электронные спектры поглощения молекул.
Часть3. Колебательные спектры поглощения молекул.
Часть 1. Общие характеристики спектров. Теоретический минимум.
· Энергия спектрального перехода.
· Энергетические характеристики.
· Диапазоны излучения и области молекулярной спектроскопии.
Спектральный переход в атоме или в молекуле вызван поглощением или испусканием электромагнитного излучения. Электромагнитное излучение состоит из частиц-фотонов, не имеющих массы покоя. Энергия фотона E определяется частотой излучения и равна Eh Коэффициент пропорциональности - константа Планка, равная h = 6.62710-34 Джс=6.62710-27 эргс. Поглощение фотона приводит к возбуждению атома или молекулы с более низкого уровня E на более высокий энергетический уровень E * . Баланс энергии при переходе описывается уравнением Планка-Эйнштейна
.
Уровни дискретны, и поглощаемые энергии также дискретны.
Поэтому регистрируемые частоты образуют также дискретное множество, и их можно нумеровать индексами уровней:
.
В большинстве молекулярных спектрах в первую очередь проявляется переход с основного на первый возбуждённый уровень. Единицы измерения энергии диктуются возможностями наиболее точной калибровки регистрирующего устройства.
В области оптической спектроскопии излучение разделяют с помощью дифракционных решёток, призм, линз. Очень хорошо разработаны способы точного измерения длин волн. Поэтому и энергию излучения принято калибровать в таких единицах, которые наиболее соответствуют конкретной экспериментальной технике. Такой единицей является обратная длина волны 1/
. Её называют волновым числом и обозначают 
.
Вся накопленная до настоящего времени информация об энергиях переходов выражается в обратных сантиметрах (см-1 ). Этим обстоятельством диктуется выбор системы единиц. Удобна система СГС (сантиметр, грамм, секунда). Единица энергии в ней ЭРГ.
Связь длины волны с частотой обратно пропорциональная, а с волновым числом прямо пропорциональная, константа пропорциональности – скорость света c =31010 см/с=3108 м/с:
.
Отсюда уравнение Планка –Эйнштейна можно представить в виде
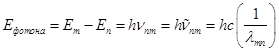
На этом основании можно уровни энергии непосредственно выразить в единицах волнового числа. Так поступают в атомной спектроскопии.
Если измерено волновое число спектрального перехода, то одно из равенств даёт
Следуя этой формуле, уровни энергии можно выразить в единицах волнового числа. Для этого следует разделить их на скорость света и константу Планка
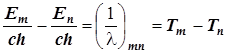
Так поступают в атомной спектроскопии.
Уровни энергии, выраженные в единицах волнового числа, называют спектральными термами . Это величины Tn и Tm .
Электронные переходы в молекулах осуществляются ориентировочно в области значений волновых чисел порядка 104 см-1 .
Длины волн такого излучения лежат в диапазоне 10-4 10-5 см.
Это сотни нанометров (1 нм=10-9 м=1010-8 см=10 A0 ).
Область цветного зрения человека охватывает длины волн 400-700 нм.
Непосредственно к этой области примыкают диапазоны:
- ультрафиолетовый со стороны квантов большей энергии и
- инфракрасный со стороны квантов меньшей энергии.
Обычная область изучения валентных электронных возбуждений молекул охватывает видимый и ближний ультрафиолетовый диапазоны.
Колебательные переходы в молекулах осуществляются ориентировочно в области значений волновых чисел порядка 102 103 см-1 .
Длины волн такого излучения лежат в диапазоне 10-2 10-3 (до 10-4 ) см.
Это инфракрасный диапазон излучения. С ним граничит видимый (со стороны
больших энергий) и микроволновой (со стороны меньших энергий)
Обычная область изучения молекулярных колебаний охватывает инфракрасный диапазон и примыкает к диапазонам излучений видимого (обертоны колебаний) и микроволнового (вращательно-колебательные движения молекул).
Часть 2. Электронные спектры поглощения. Электронные спектры красителей и модель одномерного ящика.
Для химии наибольший интерес представляют спектральные переходы электронов между уровнями граничных орбиталей молекул (ВЗМО и НСМО).
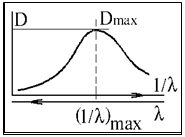
Наиболее лабильные внешние валентные электроны молекул переходят на близлежащий вакантный уровень. Электронные спектры молекул обычно регистрируют в виде широких полос с достаточно выраженным максимумом поглощения (рис. ).
Среди всех регистрируемых полос электронного спектра при переходе ВЗМО«НСМО частота, волновое число и энергия кванта минимальны, а длина волны максимальна. Реальные полосы часто не столь гладкие кривые из-за дополнительных переходов в молекуле...
Полезно рассмотреть задачу, в которой измеренные энергетические параметры электронных спектров удаётся количественно связать с уровнями граничных МО. Это классическая задача о максимумах полос поглощения в электронных спектрах карбоцианиновых красителей, решённая Бейлисом и Куном.
Примитивная модель одномерного потенциального ящика оказывается на удивление точной при описании энергий возбуждения ВЗМО«НСМО.
Задача 1
В гомологическом ряду, образованном четырьмя карбоцианиновыми красителями измерены максимумы полос электронных спектров поглощения. Формулы соединений и
измеренные величины следующие. Определите длину повторяющегося молекулярного фрагмента в гомологическом ряду полиенов.
|
Таблица.
Исходные данные, промежуточные вычисления и конечный результат
| Измерено | Вычисления студентов в ходе решения задачи | |||
| max | max см-1 | (9+2k)max | Значения 1/a 2 | aCH , |
| k | Экспер. | см | ||
| 0 | 5900 | 16949.15 | 916949 = 152540 | 5.03251015 |
| 1 | 7100 | 14084.50 | 1114084 = 154924 | 5.11171015 |
| 2 | 8200 | 12195.12 | 1312195 = 158535 | 5.23051015 |
| 3 | 9300 | 10752.69 | 1510753 = 161295 | 5.31961015 |
| Усреднение | 0.51741016 | 1.3910-8 | ||
1) Предварительные соображения .
Частота спектрального перехода при электронном возбуждении молекулы отчётливо изменяется с увеличением числа звеньев в мостике -( C=C)k -. Простейшая из характеристик этой цепи – её длина. Она складывается из длин связей разной кратности -C-C- и -C=C-.
В цепи сопряжения эти длины чередуются но, как известно, частично выравниваются. Однако их суммарная протяжённость почти не меняется.
2) Нам предстоит :
– связать наблюдаемые длины волн или частоты поглощаемого излучения с абсолютными размерами молекул с помощью теоретической модели,
– вычислить усреднённую длину связи C C в цепи -сопряжения из имеющихся спектральных данных.
–сравнить результаты расчёта с экспериментальными данными.
3) Примем во внимание, что
– Атомы C и N являются соседями в Периодической системе. Экспериментальные длины связей с одинаковой кратностью, т.е. C-C и C-N, или C=C и C=N, или CC и CN примерно равны, и в расчётах будем считать их равными.
4) Максимально упростим вычисления. Для этого
– не будем разделять связи разной кратности в системе сопряжения. Пренебрежём малыми отличиями их длин, и введём усреднённую длину связи, обозначая её a .
5) Отметим, что
5.1 Простейшая теоретическая модель для одной частицы в квантовой механике это известная модель одномерного потенциального ящика, в которой уровни энергии зависят от линейной протяжённости системы.
5.2 Модель ящика используем для граничных -электронов, которые находятся на высшей занятой МО (ВЗМО).
5.3 С ВЗМО электрон в молекуле полиена совершает спектральный переход, на ближайшую низшую свободную МО (НСМО). Её также называют низшей вакантной МО (НВМО).
5.4 Примем, что область делокализации -электронов, в том числе и на граничной занятой МО охватывает не только всю систему сопряжения, но и простирается далее за неё (для простоты примем по половине связи). Вследствие принципа Гейзенберга электрон невозможно локализовать.
5.5 При спектральном возбуждении молекулы поглощается фотон, и за счёт поглощённой энергии один электрон совершает переход между граничными МО (-ВЗМО -НВМО).
5.6 Энергия перехода, а с нею длина волны, частота и волновое число поглощаемого излучения определяется разностью уровней DE этих двух граничных МО (ГМО).
5.7 Энергетические уровни ГМО необходимо выразить как функции от длины полиеновой цепи между двумя одинаковыми концевыми гетероциклическими азотсодержащими остатками в молекулах соединений в изучаемом ряду красителей.
6) Применим для этих красителей модель свободного электрона (ящика).
Цель эадачи состоит в том, чтобы проверить, насколько абсолютные уровни энергии электронов, “размазанных ” на делокализованных- пи-МО в молекулах органических полиенов согласуются с моделью одномерного потенциального ящика.
Примечания : Введённые допущения дополняют теорию МОХ, и ей не противоречат. В простой теории МОХ не используются в явной форме структурные признаки, в том числе длины связей и размеры молекулы. В простой теории МОХ отсутствует физически конкретная шкала энергии. Единицей энергии является отвлечённый параметр - хюккелевский резонансный интеграл.
Первый шаг в расчёте - построение теоретической модели и выяснение схемы вычислений:
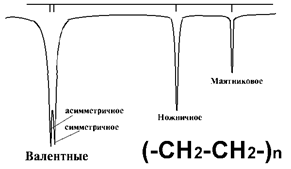
6.1) Правило квантования уровней ящика: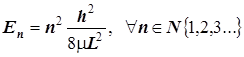 
.
6.2) Номер граничного уровня -ВЗМО равен числу электронных пар – числу двойных связей. В кольцах и вне полиенового мостика это число равно 4 и в полиеновом мостике ещё kи всего получаем число -электронных пар (4+k), это же есть и номер ВЗМО (4+k) (см. структурную формулу). Номер m уровня НВМО , на которую при возбуждении переходит электрон, на 1 больше, и равен m = n +1=4+k+1=5+k.
6.3) То же самое число (4+k) равно количеству чередующихся фрагментов с двойной и одинарной связью типа C = C - C между двумя атомами N . Длина фрагмента N + = C - C ( или N - C = C ) в циклах считается равной C = C - C . Если усреднённая из-за сопряжения длина связи C C равнаa , то длина двух связей в звене цепи сопряжения равна 2a , и расстояние между атомами N равно 2(4+k) a .
6.4) Учтём дополнительную протяжённость электронного облака за пределы системы сопряжения, добавляя к ней ещё одну длину связи. В таком случае длина ящика L , в котором делокализован электрон, равна L = 2(4+k)a +a = (9+2k)a .
6.5) Подытожим только что полученные расчётные формулы:
|
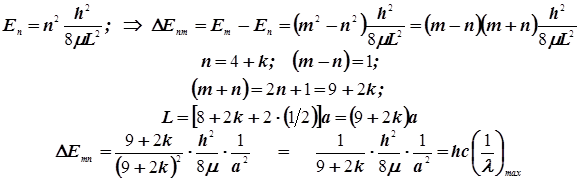
6.6) Необходимые постоянные в СГС:
m =9.1 10 -28 г (масса электрона),
c =3 1010 см/ c (скорость света),
h = 6.62 10-27 э c (константа Планка).
О размерности энергии 1 эрг=1э=1днсм=1гсмс2 см=1гсм2 с2 .
Окончательно подставляем в формулу и получаем
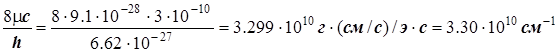
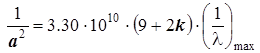
Можно вычислить усреднённую длину связи.
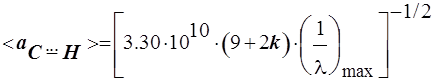
Вначале удобно вычислить величины 1/a
2
, затем их арифметически усреднить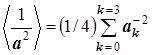 
, и из усреднённого квадрата длиныв завершение извлечь квадратный корень. Результат расчёта представлен в таблице в нижней клетке последнего столбца....
Это величина равна
,
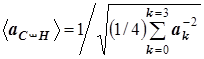Её-то и отождествим с искомым значением усреднённой длины связи СС.
Сравним результат с табличными данными.
У одинарная связи C-C в молекуле этана длина 1.53 А0 .
У двойной связи C= C в молекуле этена длина 1.33 А0 .
Длина выровненной связи C C в молекуле бензола 1.39 А0 .
Простое арифметическое усреднение даёт a =1.43 А0
Расчёт из электронных спектров дал a =1.39 А0
в бензоле a =1.39 А0
Согласие удивительное !!! Особенно с бензолом !!!
Конечно же, нами был использован ряд приёмов подгонки...
В данной задаче продемонстрирован довольно типичный набор приёмов, которыми пользуются химики в отсутствие достаточно строгих способов расчёта молекулярных характеристик.
ДОМАШНЕЕ ЗАДАНИЕ по разделу:
Даниэльс-Олберти, стр. Раздел 15.14, задача-пример 15.6,
Задачи 15.64, 15.65
Часть 3. Молекулярные колебания. Константа упругости химической связи. Колебательные деформации ядерного остова. Амплитуды колебаний. Спектры ИК-поглощения.
Вводная теория (если нет времени, можно опустить )
Природа молекулярных колебаний
|
Истинный энергетический уровень связывающего состояния 2-х атомной молекулы не может совпадать непосредственно с минимумом потенциальной кривой
в адиабатическом приближении. Это означало бы нарушение принципа Гейзенберга R p x h .
Если R R 0 , тоR 0, и это невозможно...!!!
Проблема решается за счёт поднятия истинного уровня над минимумом, и при R = R 0 возникает необходимый диапазон отклонений R 0. Они периодичны – это колебания. Максимальное отклонение от положения равновесия– амплитуда колебания.
Потенциал молекулярных колебаний. Амплитуда.
Около минимума вблизи R
0
адиабатический потенциал – энергетическую кривую можно аппроксимировать параболой
. Периодически меняющееся смещение равно x
=R
-
R
0
. Движение ядер с параболическим потенциалом – гармоническое колебание
. Его законы, полученные в классической физике, в основном справедливы и в квантовой механике. Справедливы известные соотношения. Потенциальная энергия и силовая константа равны 
Формула квантования энергии осциллятора: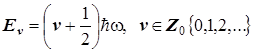 
Возбуждение молекулярных колебаний при поглощении излучения.
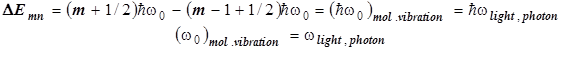
Так, регистрируя резонансную частоту поглощаемого излучения, тем самым измеряем и собственную частоту молекулярного колебания.
Валентные колебания (периодические смещения ядер от равновесия ):
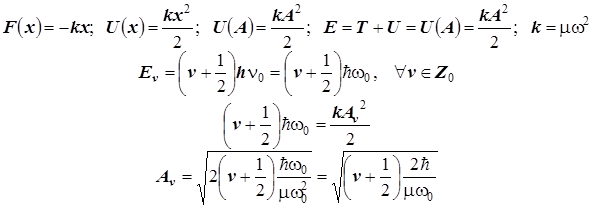
Здесь представлены величины:
Колеблющаяся масса связи A - B рассчитывается как приведённая величина:
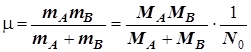
N 0 - число Авогадро, MA , MB – молекулярные массы в у.е.,
2 =2c(1/) - Круговая частота колебания.
Последняя формула позволяет вычислить амплитуду колебания на основании его собственной частоты. Линейное колебание это простейший вид молекулярной деформации.
Если оно состоит лишь в удлинении и сокращении связи, то называется валентным . Амплитуда вычисляется на основании лишь собственной частоты и даёт возможность количественно и наглядно оценить степень деформируемости молекулы.
ПРИМЕРЫ Вы найдёте в кафедральном практикуме-СБОРНИКЕ Методические указания к лабораторным работам по курсу “Физическая химия” 1985год. “колебательная спектроскопия”, 4.5.2.Стр. 41-44, а также в новом практикуме 2002 года издания
Задача 2.
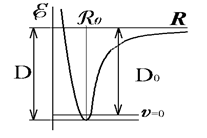
В спектре ИК-поглощения полиэтилена (-CH2 -CH2 -)2 наблюдается сравнительно небольшое число хорошо выделенных колебательных полос. Это полосы с частотами (волновыми числами) (720, 1420, 2800, 2900) см-1 . Две первые полосы принадлежат деформационным колебаниям (маятниковому и ножничному). Полосы 2800, 2900 см-1 принадлежат валентным колебаниям. Рассчитать амплитуды валентных колебаний на двух низших уровнях (v =0, 1).
|
Рис. ИК-спектр Полиэтилена (тонкая плёнка)
РЕШЕНИЕ. Удобно выполнить в системе СГС. (Вы можете сделать это и в системе СИ).
В обоих этих колебаниях колеблющаяся масса одна и та же. Это приведённая
1) Приведённая масса связи C-H равна CH = [(121)/ (12+1)] / 6.0231023 г =1.53310 -24 г
2) В обоих валентных колебаниях (симметричном 2860 и асимметричном 2950) синхронно движутся ядра двух атомов водорода, поэтому колеблющаяся масса удваивается и равна 21.53310 -24 г » 3.0710 -24 г
3) Круговая частота колебания равна 2c (1/)=6.2831010 2850 =5.3691014 рад/с
4) Величина 
= (6.6210-27
/2)/ (3.0710 -24
5.3691014
)= 0.6410-18
см2
5) Амплитуда нулевого колебательного уровня:
A0 =(0.6410-18 см 2 )1/2 » 0.810-9 см =0.08 A0
6) Это значение примерно на порядок менее длины связи.
7) Амплитуда первого колебательного уровня:
A0 =(30.6410-18 см 2 )1/2 » 1.3910-9 см » 0.14 A0
Амплитуда возрастает на возбуждённых уровнях....
ВЫВОД
Известно, что длина химической связи C-Hв соединениях равна 1.06 - 1.1 A0 .
Найденные амплитуды имеют разумные физические значения, составляя в основном и близлежащем возбуждённом состояниях 8-14% от длины связи.
Деформационные колебания (периодические изменения валентных углов ): (эти вычисления Вы выполняете по мере возможности)
Периодические изменении валентных углов называются деформационными колебаниями. В этом случае амплитуда уже не линейная, а угловая.
Воспользуемся известными аналогиями в описании поступательного и вращательного движений. При переходе от линейного к вращательному движению следует заменить:
линейное смещение x -угловым отклонением .
линейную амплитуду A - угловой амплитудой .
массу - моментом инерции I .
Константа упругости линейного колебанияk = заменяется аналогичной константой упругости углового (деформационного) колебания =I
Формула для расчёта линейной амплитуды превратится в формулу для вычисления угловой амплитуды.
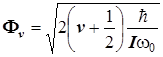
Задача 2.
В спектре ИК-поглощения полиэтилена (-CH2 -CH2 -)2 наблюдается сравнительно небольшое число хорошо выделенных колебательных полос. Это полосы с частотами (волновыми числами) (720, 1420, 2800, 2900) см-1 . Две первые полосы принадлежат деформационным колебаниям (маятниковому и ножничному). Две последние полосы принадлежат валентным колебаниям. Рассчитать амплитуды деформационных колебаний на основных уровнях (v =0).
Пример расчёта смотри в практикуме
“Методические указания к лабораторным работам по курсу “Физическая химия””
1985год. “колебательная спектроскопия”, 4.5.2.Стр. 41-44.
Указание . В этой задаче главный упор делается на вычисление моментов инерции. У маятникового колебания он равен удвоенному моменту инерции связи C-H. У ножничного равен половине момента инерции связи C-H.
Повороты отдельных связей принимаются относительно атома C.