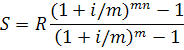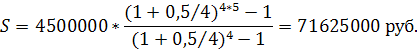Мультипликативная модель Хольта-Уинтерса

СОДЕРЖАНИЕ: Построение адаптивной мультипликативной модели Хольта-Уинтерса с учетом сезонного фактора и согласно параметрам сглаживания. Средняя ошибка аппроксимации. Определение коэффициентов заданного линейного уравнения. Проверка точности построенной модели.

Задания к контрольной работе.

Задание 1.

В каждом варианте приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство (в условных единицах) за 4 года (всего 16 кварталов, первая строка соответствует первому кварталу первого года).

Требуется:

1) Построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, приняв параметры сглаживания ₁ =0,3; ₂ =0,6; ₃ =0,3.

2) Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации.

3) Оценить адекватность построенной модели на основе исследования:

- случайности остаточной компоненты по критерию пиков;

- независимости уровней ряда остатков по d-критерию (критические значения d₁ , = l,10 и d₂ =1,37) и по первому коэффициенту автокорреляции при критическом значении r₁ =0,32;

- нормальности распределения остаточной компоненты поR/S-критерию с критическими значениями от 3 до 4,21.

4) Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.

5)Отразить на графике фактические, расчетные и прогнозные данные.

Квартал	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Вариант 9	41	52	62	40	44	56	68	41	47	60	71	44	52	64	77	47

Решение:

1. Построение адаптивной мультипликативной модели Хольта-Уинтерса:

Исходные данные:

Таблица 1.

t	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Y(t)	41	52	62	40	44	56	68	41	47	60	71	44	52	64	77	47

Для оценки начальных значений а(0) и b(0) применим линейную модель к первым 8 значениям Y(t) из таблицы 1. Линейная модель имеет вид:

Y_p (t) = a(0) + b(0) * t

Определим коэффициенты линейного уравнения а(0) и b(0) по формулам:

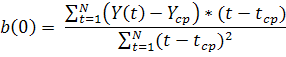
Произведем расчеты в Excel (рис.1):

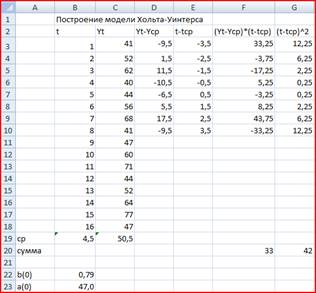
Рис .1 расчеты в Excel

Уравнение с учетом полученных коэффициентов имеет вид:

Y_p (t) = 47 + 0,79*t

Из этого уравнения находим расчетные значения Y_p (t) и сопоставляем их с фактическими значениями (рис. 2):

Рис. 2

Такое сопоставление позволяет оценить приближенные значения коэффициентов сезонности кварталов F(-3), F(-2), F(-1) и F(0) Эти значения необходимы для расчета коэффициентов сезонности первого года F(1), F(2), F(3), F(4) и других параметров модели Хольта –Уинтерса.

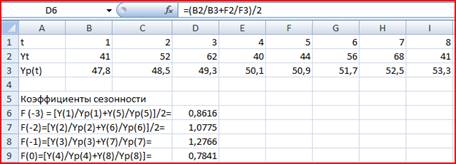
Рис. 3

Оценив значения а(0) и b(0), а также F(-3), F(-2), F(-1), F(0) перейдем к построению адаптивной модели Хольта Уинтерса.

Рассчитаем значения Yp(t), a(t), b(t), F(T) для t=1 значения параметров сглаживания 1=0,3, 2=0,6, 3=0,3.

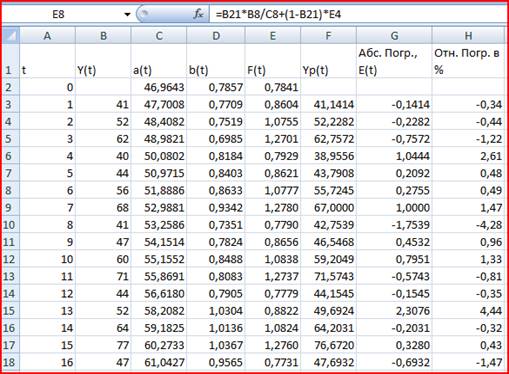
Рис. 4

2. Проверка точности построенной модели.

Условие точности выполнено, если относительная погрешность в среднем не превышает 5%.

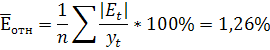
1,26%5%, следовательно, условие точности выполнено.

3. Оценка адекватности построенной модели.

3.1 Проверка случайности уровней.

Гипотеза подтверждается если P q, где

Функция int означает, что от полученного значения берется только целая часть.

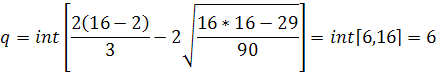
Из таблицы P = 10, 610, т.е. можно заключить, что гипотеза выполнена.

3.2 проверка независимости уровней ряда остатков (отсутствия автокорреляции). Проверка проводится двумя методами:

а) по d-критерию Дарбина – Уотсона: табличные значения d₁ = 1,08, d₂ = 1,36

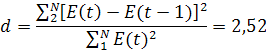
В данном случае имеет место отрицательная автокорреляция. В таком случае величину d уточняем, вычитая полученное значение из 4.

d’ = 4 – d = 4-2,53 = 1,48

Уточненное значение d сравниваем с табличными значениями d1 и d2, в данном случае d₁ =1,1 и d₂ =1,37.

Так как d₂ 1,482, то уровни ряда остатков являются независимыми.

б) по первому коэффициенту автокорреляции

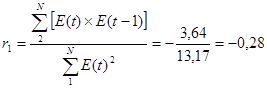
Для нашей задачи критический уровень r_таб = 0,32 - значит уровни независимы.

3.3 Проверка соответствия ряда остатков нормальному распределению по R/S-критерию с критическими значениями от 3 до 4,21.

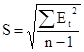, где , S = 0,93

Рис. 5

Полученное значение не попало в заданный интервал.

4. Построим точечный прогноз на 4 шага вперед.

Находим прогнозные значения экономического показателя для Y_p (t)

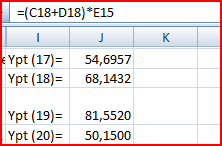
Рис. 6

5. Отразим на графике расчетные, фактические и прогнозные данные.

Рис. 7 Сопоставление расчетных и фактических данных.

Из рисунка видно, что расчетные данные хорошо согласуются с фактическими, что говорит об удовлетворительном качестве прогноза.

Задание 2.

Даны цены (открытия, максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным пяти дням. Рассчитать:

экспоненциальную скользящую среднюю;

момент;

скорость изменения цен;

индекс относительной силы;

%R, %K и %D.

Расчеты выполнить для всех дней, для которых эти расчеты можно выполнить на основании имеющихся данных.

Вариант 9
Дни	Цены
	Макс.	Мин.		Закр.
1	650		618	645
2	680		630	632
3	657		627	657
4	687		650	654
5	690		660	689
6	739		685	725
7	725		695	715
8	780		723	780
9	858		814	845
10	872		840	871

Решение:

Введем исходные данные:

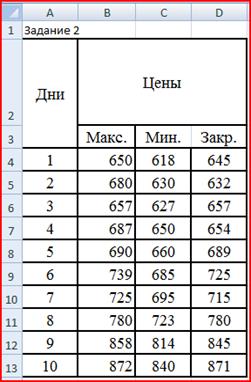
Рис. 8

Экспоненциальная скользящая средняя (ЕМА) определяется по формуле:

EMA_t = C_t *K + EMA_t-1 *(1- K)

Где ,

C_t – цена закрытия

n– интервал сглаживания, n=5

Для вычисления экспоненциальной средней сформируем таблицу:

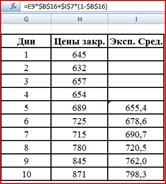
Рис. 9

Момент (МОМ) рассчитывается как разница конечной цены текущего дня и цены n дней тому назад:

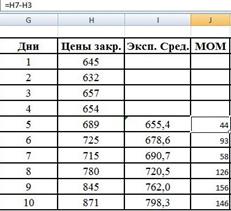
Рис. 10

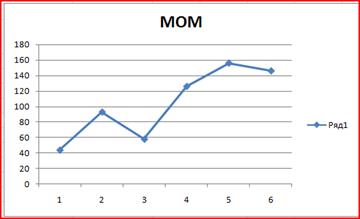
Рис. 11

Движение графика момента вверх (рис. 11) свидетельствует о повышении цен.

Скорость изменения цен (ROC):

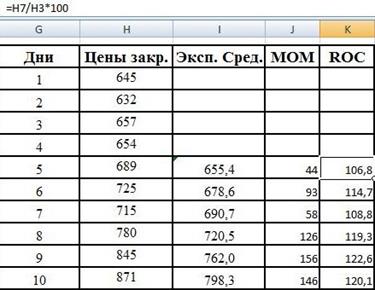
Рис. 12

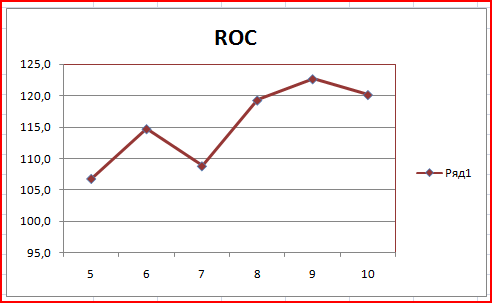
Рис. 13

ROC является отражением скорости изменения цены , а также указывает направление этого изменения. В качестве нулевой линии используется уровень 100%. Нахождения индекса выше линии 100 и положительная динамика в 7-9 дни говорит о сигнале к покупке. На 7-8 день скорость изменения цен была максимальной.

Индекс относительной силы (RSI).

Значения RSI изменяются от 0 до 100. Этот индикатор может подавать сигналы либо одновременно с разворотом цен, либо с опережением, что является важным его достоинством.

Для его расчета применяется формула:

Где AU – сумма приростков конечных цен за n дней;

AD – суммы убыли конечных цен за n дней.

Повышение цены рассчитываем по формуле: =ЕСЛИ((H5-H4)0;H5-H4;), а понижение =ЕСЛИ((H4-H3)0;ABS(H4-H3);)

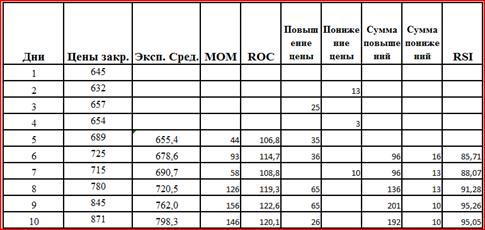
Рис. 14

Отобразим на графике полученные значения RSI (рис. 15).

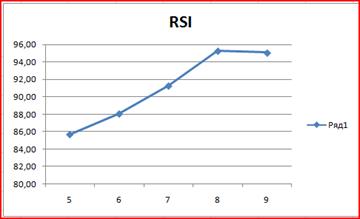
Рис. 15

Зоны перепроданности располагаются обычно ниже 25-20, а перекупленности - выше 75-80. Сигналом служит разворот RSI в указанных зонах и выход из нее. Как видно из рисунка, индекс относительной силы вошел в зону, ограниченной линией 80%, на 6-10 день. Это значит, что цены поднялись слишком высоко, надо ждать их падения и подготовится к продаже. Сигналом к продаже послужит момент выхода графика из зоны перепроданности.

Стохастические линии.

Смысл индексов %К и %R состоит в том, что при росте цен цена закрытия бывает ближе к максимальной цена ,а при падении цен, наоборот, ближе к минимальной. Индексы %R и %К проверяют куда больше тяготеет цена закрытия.

Где %K_t – значение индекса текущего дня;

C_t – цена закрытия текущего дня;

L₅ и H₅ – соответственно минимальная и максимальная цены за 5 предшествующих дней, включая текущий.

Где %R_t – значение индекса текущего дня, t;

C_t – цена закрытия текущего дня t;

L_n и H_n – соответственно минимальная и максимальная цены за n предшествующих дней, включая текущий.

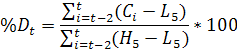
Составим таблицу расчета индексов стохастических линий и заполним ее (рис. 18).

В ячейку Е8 введем формулу =МАКС(B4:B8) и размножим ее, а в ячейку F8 формулу =МИН(C4:C8) и тоже размножим (рис. 16)

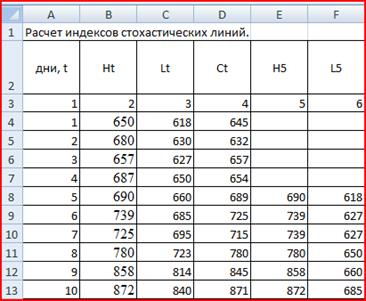
Рис. 16

В ячейку G8 введем формулу =D8-F8, в H8 =E8-D8, в I8 =E8-F8 и размножим их (рис. 17).

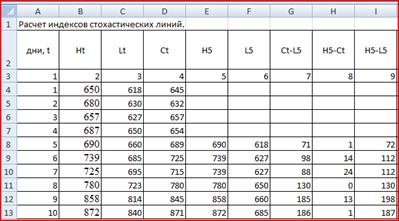
Рис. 17

Далее рассчитаем индексы (рис. 18).

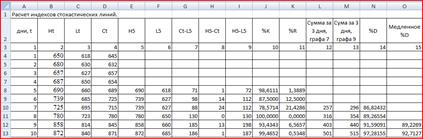
Рис. 18 расчет индексов стохастических линий.

Медленное %D рассчитывается по формуле =СРЗНАЧ(N10:N12).

Критические значения %К (зона перекупленности) свидетельствуют о том, что можно ожидать скорого разворота тренда, т.е. падения цен.Как видно из графика и из таблицы если цена закрытия ближе к максимальной цене, то наблюдается рост цен , в противном случае, падение (рис. 19).

Рис. 19 Ценовой график.

Задание 3.

Выполнить различные коммерческие расчеты, используя данные, приведенные в таблице. В условии задачи значения параметров приведены в виде переменных. Например, S означает некую сумму средств в рублях, Т _лет - время в годах, i - ставку в процентах и т.д. По именам переменных из таблицы необходимо выбрать соответствующие численные значения параметров и выполнить расчеты.

Вариант	Сумма	Дата начальная	Дата конечная	Время в днях	Время в годах	Ставка	Число начислений
Вариант	S	T_H	T_K	T_дн	T_лет	I	m
9	4500000	09.01.02	21.03.02	90	5	50	4

3.1 Банк выдал ссуду, размером S руб. Дата выдачи ссуды - T_H , возврата - T_K . День выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой процентной ставке i % годовых.

Найти:

3.1.1) точные проценты с точным числом дней ссуды;

3.1.2) обыкновенные проценты с точным числом дней ссуды;

3.1.3) обыкновенные проценты с приближенным числом дней ссуды.

3.2 Через T_дн дней после подписания договора должник уплатит S руб. Кредит выдан под i % годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?

3.3Через T_дн дней предприятие должно получить по векселю Sруб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке i % годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт.

3.4 В кредитном договоре на сумму S руб. и сроком на T_лет лет, зафиксирована ставка сложных процентов, равная i % годовых . Определить наращенную сумму.

3.5 Ссуда, размером S руб. предоставлена на Т_лет . Проценты сложные, ставка i % годовых. Проценты начисляются m раз в году. Вычислить наращенную сумму.

3.6 Вычислить эффективную ставку процента, если банк начисляет проценты m раз в году, исходя из номинальной ставки i % годовых.

3.7 Определить, какой должна быть номинальная ставка при начислении процентов m раз в году, чтобы обеспечить эффективную ставку i % годовых.

3.8 Через Т_лет предприятию будет выплачена сумма S руб. Определить ее современную стоимость при условии, что применяется сложная процентная ставка i% годовых.

3.9 через Т_лет по векселю должна быть выплачена сумма S руб. Банк учел вексель по сложной учетной ставке i % годовых. Определить дисконт.

3.10 В течение Т_лет на расчетный счет в конце каждого года поступает по S руб., на которые m раз в году начисляются проценты по сложной годовой ставке i%. Определить сумму на расчетном счете к концу указанного срока.

Решение.

3.1Используем формулу: