На тему

СОДЕРЖАНИЕ: С моей точки зрения, симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту, совершенство. Слово симметрия издавна употреблялось в значении гармония. Термин «гармония» в переводе с греческого означает, соразмерность, одинаковость в расположении частей

Отдел образования администрации МО «Черноярский район»

Экспериментальная площадка программы «Интеллект»

МОУ «Средняя общеобразовательная школа с.Солодники.»

Реферат

На тему:

Выполнила:

Попова Екатерина,

Ученица 9 кл.

Руководитель:

Богданова Н.И.

Учитель Математики

с.Солодники

2008.

План

I. Введение

II. Основная часть

1.Симметрия с математической точки зрения.

2.Симметрия в жизни человека.

3.Симметрия в окружающей природе.

III. Заключение.

Литература.

Введение

Я в листочке, я в кристалле,

Я в живописи, архитектуре,

Я в геометрии, я в человеке.

Одним я нравлюсь, другие

Находят меня скучной.

Но все признают, что

Я – элемент красоты.

Данный реферат посвящен такому понятию современного естествознания, как симметрия. Лейтмотивом моего реферата является понятие симметрии, играющей ведущую хотя и не всегда осознанную роль в современной науке, искусстве, технике и окружающей нас жизни .Симметрия пронизывает буквально все вокруг ,захватывая, казалось бы, совершенно неожиданные области и объекты.Я считаю здесь уместно привести высказывание Дж. Ньюмена, который особенно удачно подчеркнул всеохватывающие и ведущие проявления симметрии: «Симметрия устанавливает забавное и удивительное сходство между предметами, явлениями и теориями, внешне, казалось бы, ничем не связанными: земным магнетизмом, женской вуалью, поляризованным светом, естественным отбором, теорией групп, инвариантами и преобразованиями, рабочими привычками пчел в улье, строением пространства, рисунками ваз, квантовой физикой, скарабеями, лепестками цветов, интерференционной картиной рентгеновских лучей, делением клеток морских ежей, равновесными конфигурациями кристаллов, романскими соборами, снежинками, музыкой, теорией относительности».

С моей точки зрения, симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту, совершенство. Слово симметрия издавна употреблялось в значении гармония. Термин «гармония» в переводе с греческого означает, соразмерность, одинаковость в расположении частей.

Ежедневно нас интересуют такие вопросы как: Почему мы находим одни вещи красивыми, а другие нет? Почему некоторые люди кажутся нам более привлекательными, а другие менее? К примеру супермодель – Кристи Тарлинктон, признанная одной из самых красивых женщин в мире, - считает, что по большей части обязана своим успехом в качестве модели идеальной симметрии своих губ. Пропорция и симметрия объекта всегда необходимы нашему зрительному восприятию для того, чтобы мы могли считать этот объект красивым. Баланс и пропорция частей относительно целого обязательны для симметрии. Смотреть на симметричные изображения приятнее, нежели на асимметричные.

Главную цель, которую я поставила для себя – это изучить такое понятие, как симметрия и научиться различать виды симметрии в окружающем мире, увидеть красоту симметрии в природе, как один из факторов гармонии и красоты.

Гравюра Эшера «Ящерицы»

Симметрия с математической точки зрения

Математически строгое представление о симметрии сформировалось сравнительно недавно – в XIXв. В наиболее простой трактовке известного немецкого математика Германа Вейля (1895–1955) современное определение симметрии выглядит так: симметричным называется такой объект, который можно как-то изменять, получая в результате то же с чего начали. «Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство».

Современное представление о симметрии предполагает неизменность объекта по отношению к каким-то преобразованиям, выполняемым над ними.

Пифагор показал, что отрезок АВ единичной длины можно разделить на две части так, что отношение большей части (АС=х) к меньшей (СВ=1-х) будет равно отношению всего отрезка (АВ=1) к большей части (АС) : ,то есть .Отсюда х=1-х, Положительным корнем этого уравнения является , так что отношение в приведенной пропорции равно

… Такое деление Пифагор назвал золотым делением , или золотой пропорцией, а Леонардо да Винчи-золотым сечением, общепринятым сейчас термином. Впоследствии учение о золотом сечении получило широкое применение в математике, эстетике, ботанике, технике. Здесь мы остановимся на связи золотого сечения лишь с симметрией.

В 1202г вышло в свет сочинение «Liber abacci» («Книга об абаке») знаменитого итальянского математика Леонардо из Пизы, известного больше как Фибоначчи. В нем Фибоначчи,решал задачу о размножении кроликов, получает следующую знаменитую последовательность чисел :

0,1,1,2,3,5,8.13,21,34,55,89,144,233,377…

Фибоначчи подметил, что открытая им последовательность чисел при задается формулой , где член ряда. И.Кеплер заметил, что при возрастании .

Через 100 лет Р.Симпсон строго доказал,что .

Лишь в 1843г то есть через 641 год после открытия указанной последовательности чисел, Ж.Бине нашел формулу для -го ее члена:

Симметрия в жизни человека

Красота и гармония тесно связаны с симметрией, это подметили еще архитекторы и художники.

( Замечательная постройка XVIII века – Казанский собор.)

Слово симметрия происходит от греческого слова, которое означает «такая же мера». Греческий скульптор Поликлет, очевидно, был первым, кто использовал этот термин еще в Vв. До н. э. Во времена Пифагора и Пифагорейцев понятие симметрии было оформлено достаточно четко.В то же время

Они смогли подвергнуть его серьезному анализу и получить результаты универсального назначения. Отметим некоторые из них:

1.Для симметрии важны равенство,однообразие и пропорциональность :однообразно(в смысле подчинения какой-либо математической закономерности) располагая равные части, можно построить симметричную фигуру, скажем, квадрат из четырех равнобедренных треугольников. 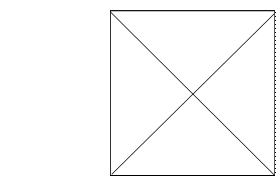Если же нарушить закон однообразия в расположении равнобедренных треугольников, то мы получим уже менее симметричную, в пределе ассиметричную фигуру.

2.Пифагорейцы выделили 10 пар противоположностей, среди них «правое» (D) и «левое» (L) из этого следует, что во-первых, понятия правого и левого в теории симметрии имеют фундаментальное значение: а) пользуясь D и L асимметричными образцовыми фигурами ( например, запятыми, неправильными треугольниками, тетраэдрами) и «размножая» их соответствующими элементами симметрии, можно построить теорию симметрии, с этой точки зрения, предстает как учение о симметрии специфических противоположностей -D и L, б) изучение природы с точки зрения D и L в дальнейшем привело к одной из важнейших проблем естествознания – к проблеме правизны и левизны.

Было обнаружено, что применяемая в ботанике для описания видов винтового расположения листьев на побеге

последовательность дробей:

во-первых , составлена из чисел ряда Фибоначчи; во-вторых, построена так, что числитель и знаменатель любой дроби ,начиная с третьей равны сумме числителей и знаменателей двух предыдущих дробей; в-третьих, стремится к пределу 0,3817…= = Ф ;в-четвертых, фактически обозначает последовательность видов винтовых осей симметрии, применяемых в теории структурной симметрии для описания симметрии бесконечных фигур. Кроме

того, выявилось, что последовательность дробей:

применяемая в ботанике же для описания спирального расположения семянок в головках подсолнечника или чешуй в сосновых шишках, так же составлена из чисел ряда Фибоначчи; построена так же, как и предыдущий ряд, только здесь знаменатель одной дроби равен числителю другой дроби, следующей за него непосредственно; стремится к пределу

0,61803…= = Ф

Причем 0,61803…=1-0,38197…,

0,61803…

0,38197… 0,61803…

то есть золотому сечению единичного отрезка фактически обозначает также последовательность видов винтовых осей симметрии.

Человеческое тело, так же как и тело других позвоночных, в основе своей построено зеркально симметрично. Внешне человек построен симметрично:

левой руке всегда соответствует правая и обе руки совершенно одинаковы.

Но! Здесь стоит остановиться. Если бы наши руки и в самом деле были совершенно одинаковы, мы могли бы в любой момент поменять их. Было бы

возможно, скажем, путем трансплантации пересадить левую ладонь на правую руку, если, проще, левая перчатка подходила бы тогда к правой руке,

но на самом деле это не так. Каждому известно, что сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметами и его отражением в зеркале именно вопросам симметрии и зеркального отражения здесь уделяем внимание. Размеры отдельных частей тела человека(за единицу измерения выбрана голова) находятся в отношении

1 : 2 : 3 : 5 : 8 и составляют ряд Фибоначчи.

Размеры головы обозначим Г . Тогда плечи равны 2Г , размах рук – 8Г , грудь – 2Г , бедро – 2Г , голень – 2Г , пояс-колени – 3Г , пояс-щиколотки - 5Г , макушка – ступня – 8Г , размах одной руки – 3Г .

С древних времен установлено, что если стопу человека принять за единицу измерения – фут, то рост человека составит 6 футов, а голова вместе с шеей – 1 фут.

Деление головы на характерные части дает целый ряд отношений, очень близких к золотому сечению. То же самое можно сказать о руке и ладони.

Общие принципы строения организма человека заложены миллиарды лет назад, когда формировался генетический код и возникла первая клетка. В наших генах содержится значительная часть генофонда древних рыб, первых хордовых и некоторых беспозвоночных животных. Одним из признаков, переданных нам, является двухсторонняя симметрия человеческого тела. Среди врачей существует мнение, что причинами наших болезней являются не только и не столько вирусы и прочие вредные факторы среды, сколько генетически обусловленные нарушения конструкции тела. «Симметричные» животные живут дольше, чем «несимметричные», что также говорит в пользу того, что симметрия – это показатель здоровья. Это также и показатель лучшей способности к воспроизводству. Асимметрия лица – это показатель старения.

Многие художники обращали пристальное внимание на симметрию и пропорции человеческого тела. Согласно канонам, составленным Альбрехтом Дюрером и Леонардо да Винчи, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат.

В современных школах живописи в качестве единой меры чаще всего принимается размер головы по вертикали. С известным допущением можно считать, что длина туловища превосходит размер головы в восемь раз. На первый взгляд это кажется странным. Но нельзя забывать , что большинство высоких людей отличаются удлиненным черепом и, наоборот, редко можно встретить низкорослого толстяка с головой удлиненной формы.

Размеру головы пропорциональна не только длина туловища, но и размеры других частей тела. По этому принципу построены все люди, оттого-то мы в общем похожи друг на друга. Однако наши пропорции согласуются лишь приблизительно, а потому люди лишь похожи, но не одинаковы. Во всяком случае, все мы симметричны! К тому же некоторые художники в своих произведениях особенно подчеркивают эту симметрию.

И в одежде человек тоже, как правило, старается поддерживать впечатление симметричности: правый рукав соответствует левому, правая пуговица-левой.

Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния.

Кроме этого украшая свою одежду, человек использовал для этого симметричные узоры. Мы живем в России и издревле в русском орнаменте присутствовала симметрия.

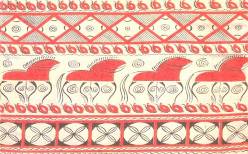
Так же издавна человек использовал симметрию в архитектуре. Симметрия придает древним храмам, башням замков, современным зданиям гармоничность и законченность.

Даже здание нашей школы построено по правилам симметрии.

А народные ремесла, такие как вязание, бисероплетение, резьба по дереву и другие в своей основе содержат различные виды симметрии.

Посмотрите на эти фотографии. Они еще раз подчеркивают мои слова о гармонии и красоте симметрии.
Бисероплетение. Ожерелье.

Ожерелье выполнено из желтого стекляруса, коричневого и золотого бисера в технике плетения «Жабо».

Рассмотрим украшение с точки зрения симметрии:

Данное ожерелье представляет собой пример зеркальной симметрии.

Вязание крючком. Салфетка. Такие салфетки я вяжу сама, посмотрите на нее.

Резьба по дереву. Отделка домов. Вот так в старину в нашем селе народные умельцы украшали свои дома.

Как видите здесь присутствуют элементы осевой симметрии.

Симметрия в окружающей природе

А вы видели тени от снежинок?

А вы знаете, как они танцуют

В лунном блеске голубом и чистом,

Или просто в свете фонаря?

Рассмотрим симметрию в окружающей нас природе на примере снежинок. С раннего детства мы сталкиваемся с таким чудом природы как снег. Любой ребенок любит наблюдать как снежинки падающие с неба тают на ладони превращаясь в каплю воды…И всегда снежинка ассоциируется у нас с таким любимым всеми праздником как Новый год. Но снежинки это не только новогоднее украшение. Это еще и китайские фонарики, кружева, салфетки, шаблоны для росписи. Они могут быть квадратными, пятиугольными, шестиугольными и круглыми, а точнее восьмиугольными. Строго говоря, природные снежинки бывают только шестиугольными или любыми другими плоскими или пространственными образованиями с количеством лучей, кратным трем. Все другие формы «снежинок» - чисто декоративные. У снежинки шесть осей симметрии. Наверное, она была бы совсем другой, если бы молекулы воды не обладали определенной симметрией. Зеркальной симметрией обычно обладают листья растений, удивительно симметричны листья дуба, вербы, клена, крапивы .

Посмотрите на кленовый лист, бабочку, снежинку.

Их объединяет то, что они симметричны. Если прочертить вертикальную прямую вдоль центральной прожилки листа и поставить зеркальце вдоль прочерченной прямой, то отраженная в зеркальце половинка фигуры дополнит ее до целой (такой же, как исходная фигура) .Поэтому такая симметрия называется зеркальной (или осевой, если речь идет о плоскости). Прямая, вдоль которой поставлено зеркало, называется осью симметрии. Если симметричную фигуру сложить вдоль оси симметрии, то ее части совпадут.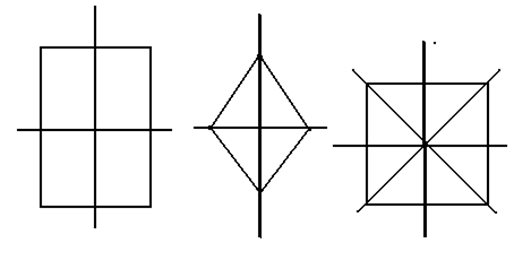

Среди цветов наблюдается поворотная симметрия. Многие цветы можно повернуть так, что каждый лепесток займет положение соседнего, цветок совместится.

Минимальный угол такого поворота для различных цветов неодинаков. Для ириса он равен 120 ,для колокольчика, цветка вишни – 72, для нарцисса – 60.

Посмотрите на цветок цветущего дерева вишни, распустившейся в садуэто наглядный пример поворотной симметрии.

В расположении листьев на стеблях растений наблюдается винтовая симметрия. Располагаясь винтом по стеблю, листья как бы раскидываются в разные стороны и не заслоняют друг друга от света.

Поворотную ось можно охарактеризовать с помощью другой величины называемой порядком оси. Эта величина показывает, сколько раз произойдет совмещение при повороте на 360. Цветы колокольчика и нарцисса обладают осями пятого и шестого порядка соответственно. Обозначим элементарный угол поворота оси буквой b ,а ее порядок буквой п. Тогда можно записать простое соотношение, которое связывает эти две величины:

п=

А цветок анютины глазки совместится сам с собой только при повороте на 360.Это значит, что цветок обладает лишь осью первого порядка. А вот плоды (яблоко или груша) достаточно правильной формы могут оказаться совмещенными сами с собой при повороте на любой в том числе сколь угодно малый угол вокруг оси, идущей вдоль черенка (естественно, при условии некоторой идеализации их формы).

Если внимательно приглядеться к стеблю растения, то окажется, что и здесь действует закон симметрии.

Оказывается, винтовое расположение листьев составлено из ряда чисел Фибоначчи, которые играют немаловажную роль в природе.

Нельзя не увидеть симметрию и ограненных драгоценных камнях . Многие гранильщики стараются придать бриллиантам форму тетраэдра, куба, октаэдра или иксаэдра. Но эти замечательные тела еще и поэтому красивы, что в основе их пропорциональных линий лежит золотая пропорция.

Однако симметрия существует и там, где ее не видно на первый взгляд. Физик скажет вам, что всякое твердое тело – это кристалл. Знаменитый кристаллограф Евграф Степанович Фролов сказал: «Кристаллы блещут симметрией». Химик скажет, что все тела состоят из атомов. А многие атомы располагаются в пространстве по принципу симметрии.

Симметрия широко распространена в природе. Мы можем видеть ее, когда смотрим на жуков, бабочек,

листья деревьев. Симметрия, характерная для представителей животного мира, называется билатерной симметрией.

Вернемся к винтовой, или спиральной симметрии. Винтовая симметрия есть симметрия относительно комбинации двух преобразований – поворота и переноса вдоль оси поворота, то есть перемещение вдоль оси винта и вокруг оси винта. Встречаются левые и правые винты. Примерами природных винтов являются: бивень нарвала – левый винт; раковина улитки – правый винт; рога памирского барана – один рог закручен по левой, а другой по правой спирали . Спиральная симметрия не бывает идеальной, например, раковина моллюсков сужается или расширяется на конце.

Спиральную структуру имеют многие важные молекулы, из которых построены живые организмы – белки, дезоксирибонуклеиновые кислоты – ДНК, являющиеся носителем наследственной информации в живом организме. Молекула ДНК имеет структуру двойной правой спирали.

Подлинным царством природных винтов является мир «живых молекул», к которым относятся прежде всего молекулы белков. Все части тела, включая кости, кровь, мышцы, сухожилия, волосы, содержат белки . Молекула белка представляет собой цепочку составленную из отдельных блоков и закрученную по правой спирали . Ее называют альфа – спиралью . За открытие альфа – спирали американский ученый Лайнус Полинг получил Нобелевскую премию, самую высшую награду в научном мире.

Заключение

В данном реферате мною была рассмотрена и изучена тема: «Этот симметричный мир». Конкретно: симметрия с математической точки зрения, симметрия в жизни человека, симметрия в окружающей природе.

Симметрию мы наблюдаем ежедневно и повсеместно,так как в мире все гармонично и симметрично. Человек использовал симметрию в строительстве жилищ, в создании предметов быта, в украшении одежды. Главную цель, которую я ставила для себя в своем реферате – это изучить такое понятие как симметрия, научиться различать виды симметрии в окружающем мире, увидеть красоту симметрии в природе, как один из факторов гармонии и красоты. Исследования, проведенные мной, показали, что симметрия, обнаруживаемая и в жизни, и в природе является одним из принципов гармоничного построения мира. «Сфера влияния» симметрии поистине безгранична. Всюду она определяет гармонию природы, мудрость науки и красоту искусства. Без симметрии нет жизни.

Подводя итоги данной работы убеждаемся в главном:

Да, путь познания не гладок,

Но знаем мы со школьных лет

Загадок больше чем разгадок

И поискам предела нет…

Используемая литература

1. Журнал Математика в школе.1993г.

2. Журнал Математика. Приложение к газете «Первое сентября»2004г.

3. Журнал Математика. Приложение к газете «Первое сентября»2005г.

4. Зоркий П.М. архитектура кристаллов. – М.: Наука, 1968г.

5. Джаффе Г., Орчин М. Симметрия в химии. - М.: Мир, 1967г.

6. Шафрановский И. И. Симметрия в природе. – Л.:Недра,1985г.

Скачать архив с текстом документа