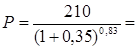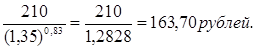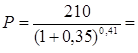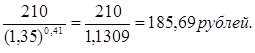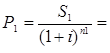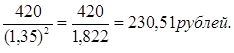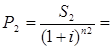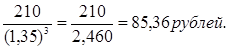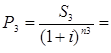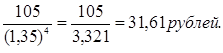Начисление сложных процентов от вклада
СОДЕРЖАНИЕ: Начисление процентов при заданном размере вклада. Поиск величины платежа при сложной ставке, номинальной ставки при заданной месячной инфляции для получения эффективности от вклада. Использование формулы математического дисконтирования сложных процентов.МОСКОВСКИЙ ИНСТИТУТ ПРЕДПРИНИМАТЕЛЬСТВА И ПРАВА
КОНТРОЛЬНАЯ РАБОТА
По дисциплине: Финансовая математика
По теме: задача №№ 1, 2, 3, 4, 5, 6, 7,8.
Направление/ Финансы и кредит
Студент: 3 курса
Адрес:
№ телефона:
Шифр зачетной книжки:
Преподаватель:
г. Новосибирск
2007
Параметры варианта:
- последняя цифра номера зачетки (если последняя цифра -0, то =10); 
предпоследняя цифра номера зачетки;
последняя цифра года рождения (если последняя цифра -0, то 
=10);
х= 4; z=3; g=1.
y=5; n=5; a=210; в=35.
Задача 1. Какая сумма будет в итоге на счете, если вклад 
= 210 руб. положен на 
=5 лет под 
=35% годовых в банк. Проценты сложные, начисление:
а) раз в год; в) ежемесячное;
б) ежеквартальное; г) ежедневное
Решение:
а) ежегодное начисление.
Дано:
P=210 руб.
S1 = P (1+i) n
n=5 лет.
i =0,35
S1 - ?
S1 = 210 (1+0,35) 5 =2104,484033438=941,64 рублей.
б) ежеквартальное начисление.
Дано:
P=210 руб.
n=5 лет.
i =0,35
m=4
S2 - ?
S2
= P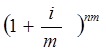
S2
= 210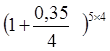
=210(1,0875)20
=1124,09 рублей
в) ежемесячное начисление.
P=210 руб.
n=5лет.
i =0,35
m=12
 |
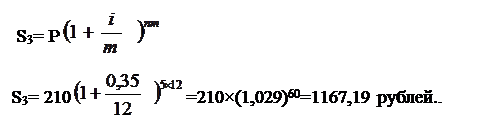S3 - ?
г) ежедневное (непрерывное) начисление.
Дано:
P=210руб.
n=5лет.
i =0,35
S4 - ?
S4 = P е in
S4 = 210 e0,355 =2102,721,75 =2105,760=1209,6 рублей.
Задача 2. Рассчитайте, какую сумму надо положить на депозит, чтобы через 4 года она выросла на а =210 руб. при в=35 % годовых.
Дано:
S=P+210руб. При решении используем формулу математического дисконтирования
n=5лет.
i =0,35
Р - ?
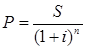
Задача 3. Через сколько лет удвоится вклад при годовой ставке =35%. Проценты начисляются:
а) ежеквартально; б) ежемесячно
Дано:
S=2P руб.
m1 =4
m2 =12
i =0,35
n1 - ?
n2 - ?
а) ежеквартально
(1,08) 4 n1 = 2; log (1,08) 4 n1 = log1,08 2; 4n1 log1,08 1,08 = log1,08 2; 4n1 =log1,08 2; 4n1 =ln2/ln1,08 ;
|
б) ежемесячно
(1,02) 12n2 = 2; log (1,02) 12n2 = log1,02 2; 12n2 log1,02 1,02 = log1,02 2; 12n2 =log1,02 2; 12n2 =ln2/ln1,08 ;
|
;
;
;
Задача 4. Платеж в =210 руб., срок выплаты 
=25 месяцев, заменить платежом со сроком:
а) 
=15 месяцев; б) 
=30 месяцев
Используется ставка =35% годовых, начисление процентов - раз в год.
10 5
-----------------------------------------------
15 дисконт 25наращ 30
|
Дано:
S=210 руб.
n=25-15=10; 
i=0,35
P-?
Дано:
S=210 руб.
n=30-25=5; 
i=0,35
P-?
|
Задача 5. Существует три платежа 
руб., со сроками выплат соответственно через 
лет заменить одним платежом через три года. Найдите величину платежа, если используется сложная ставка =35% годовых.
Так как платежи переносятся на более ранний срок, то их нужно дисконтировать.
Используем математическое дисконтирование сложных процентов.
Дано:
S1 =420
S2 =210
S3 =105
n1 =5-3=2
n2 =6-3=3
n3 =7-3=4
i=0,35
P - ?
Р=Р1 + Р2 + Р3 =230,51+85,36+31,61=347,48 рублей. |
Задача 6. Инвестор, вложив а
=210тыс. руб. получил в конце года 
=410 тыс. руб. Инфляция =1% годовых. Найдите эффективную ставку.
Дано:
P=210000
S=410000
=0,01
n=1
iэфф -?
S= P (1+i) n ; 410000=210000 (1+i) 1 ; 41 = 21 (1+i) 1 ; 1+i = i = 1+i = iэфф
= |
;
номинальная ставка;
; iэфф
= 
; iэфф
= 
;
; iэфф
= 
;; iэфф
= 93%.Задача 7. Месячная инфляция =1%. Какова должна быть назначена номинальная ставка, чтобы эффективная оказалась = 35%.
Дано:
h = 0,01
iэфф = 0,35
i - ?
Обозначим годовой индекс инфляции ч. з.1+a, Месячный индекс 1+h. 1+a = (1+h) 12 a = (1+h) 12 - 1 = (1+0,01) 12 - 1 = 0,12 т.е. годовая инфляция составила 12%. 1+iэфф
= i = (1+ iэфф ) (1+a) -1 = (1+0,35) (1+0,12) - 1 = (1,35) (1,12) - 1= = 1,512 1,51 или I = 151%. |
Задача 8. Оцените, что выгоднее: получить 
=420 руб. сразу или 
=315 руб. сейчас и 
=105 руб. через два года, если ставка =35% годовых.
Дано:
Р1 =420
Р2 =315
Р3 =105
n =2
i=0,35
S - ?
S1 =420 (1+0,35) 2 = 420 (1,35) 2 = 4201,822 =765,24 рублей; S2 =315 (1+0,35) 2 + 105 = 315 (1,35) 2 + 105 = 679,08 рублей: 765,24 679,08, по этому 420 рублей выгоднее получить сразу. |