Нахождение площади живого сечения траншеи
СОДЕРЖАНИЕ: 1. Формулировка проблемы. Сечение траншеи имеет форму близкую к сегменту параболы, ширина траншеи на её поверхности l метров наибольшая глубина H метров . найти площадь «живого сечения» траншеи , если она полностью заполнена водой.
1. Формулировка проблемы.
Сечение траншеи имеет форму близкую к сегменту параболы, ширина траншеи на её поверхности l метров наибольшая глубина H метров . найти площадь «живого сечения» траншеи , если она полностью заполнена водой.
Дано:
l=1,5 Найти: S живого сечения траншеи
Н=2,25
2. Пояснение к решению.
· Прибавляя постоянную к первообразной какой-либо функции, вновь получают первообразную той же функции. Следовательно, имея одну первообразную F(x) функции f (x), получают общее выражение всех первообразных этой функции в виде F(x) + С. (Постоянная C называется произвольной постоянной). Это общее выражение первообразных называют неопределённым интегралом.
· Приращение первообразных функций F(x)+C
при переходе аргумента x
от значения x=a
к значению x=b
, равное разности F(b)-F(a)
, называется определенным интегралом
. Определённый интеграл - это число, в отличие от неопределённого интеграла, который является группой функций. Крайние точки области интегрирования называются границами интегрирования
.Когда интеграл используется для вычисления площади, принято обозначать границы на двух концах знака интеграла и записывать так: 
.
· Функцию 
называют первообразной функции
.
· 
-дифференциал функции
и определяется следующим образом: 
· Формула Ньютона-Лейбница.
Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции , то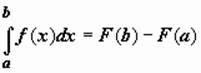 
· Уравнение параболы имеет вид y=ax2 +bx+c.
· Определенный интеграл численно равен площади под графиком функции от которой он берется, причем площади на интервале интегрирования.
· нахождение неопределенного интеграла это операция обратная нахождению производной(дифференциированию).
4. Расчетная часть.
l=1,5 м
H=2,25 м
1)y=x2 +bx+c
2)y=ax2 +c
y=ax2 -2,25, т.к точка В с координатами (х=0,75;у=0) принадлежит параболе, то её координаты удовлетворяют уравнению параболы. =
0=а0,752 -2,25; 0,752 а=2,25; 0,5625а=2,25; а=2,25/0,5625; а=4
3)f(x)=4х2 -2,25
4) Найдем площадь «живого сечения»
Т.к части графика 1 и 2 идентичны, можно их представить как 2-е одинаковые части.
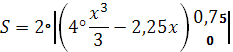
S=22,4375=4,875 м2
Ответ: площадь «живого сечения» 4,875 м3
План:
1. Формулировка проблемы.
2. Пояснение к решению.
3. Графическая часть
4. Расчетная часть.
5. Выводы
6. Используемая литература.
Вывод
Выполнив работу я закрепила знания по теме определенный интеграл, его практическое применение и приложение в реальной жизни. С помощью исходных данных при заданных условиях научилась вычислять «живую площадь» траншеи.
6.Литература