Нейронные сети
СОДЕРЖАНИЕ: Изучение человеческого мозга. История изучения и создания нейронных сетей. Биологический и искусственный нейрон. Выбор структуры нейросети. Грамотное обучение искусственных нейронных сетей и их применение, программные модели искусственных нейросетей.МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Институт математики и компьютерных наук
Реферат
на тему:
Нейронные сети
Т 2009
Содержание
История нейронных сетей
Аналогия с мозгом
Биологический нейрон
Искусственный нейрон
Обучение искусственных нейронных сетей
Применение нейронных сетей
Список литературы
История нейронных сетей
Изучению человеческого мозга - тысячи лет. С появлением современной электроники, начались попытки аппаратного воспроизведения процесса мышления. Первый шаг был сделан в 1943 г. с выходом статьи нейрофизиолога Уоррена Маккалоха (Warren McCulloch) и математика Уолтера Питтса (Walter Pitts) про работу искусственных нейронов и представления модели нейронной сети на электрических схемах.
1949 г. - опубликована книга Дональда Хебба (Donald Hebb) Организация поведения, где исследована проблематика настройки синаптических связей между нейронами.
1950-е гг. - появляются программные модели искусственных нейросетей. Первые работы проведены Натаниелом Рочестером (Nathanial Rochester) из исследовательской лаборатории IBM. И хотя дальнейшие реализации были успешными, эта модель потерпела неудачу, поскольку бурний рост традиционных вычислений оставил в тени нейронные исследования.
1956 г. - Дартмутский исследовательский институт искусственного интеллекта обеспечил подъем искусственного интеллекта, в частности, нейронных мереж. Стимулирование исследований искусственного интеллекта разделилось на два направления: промышленные применения систем искусственного интеллекта (экспертные системы) и моделирование мозга.
1958 г. - Джон фон Нейман (John fon Neumann) предложил имитацию простых функций нейронов с использованием вакуумных трубок.
1959 г. - Бернард Видроу (Bernard Widrow) и Марсиан Хофф (Marcian Hoff) разработали модели ADALINE и MADALINE (Множественные Адаптивные Линейные Элементы (Multiple ADAptive LINear Elements)). MADALINE действовала, как адаптивный фильтр, устраняющих эхо на телефонных линиях. Эта нейросеть до сих пор в коммерческом использовании.
Нейробиолог Френк Розенблатт (Frank Rosenblatt) начал работу над перцептроном. Однослойный перцептрон был построен аппаратно и считается классической нейросетью. Тогда перцептрон использовался для классификации входных сигналов в один из двух классов. К сожалению, однослойный перцептрон был ограниченым и подвергся критике в 1969 г., в книге Марвина Мински (Marvin Minsky) и Сеймура Пейперта (Seymour Papert) Перцептроны.
Ранние успехи, способствовали преувеличению потенциала нейронных мереж, в частности в свете ограниченной на те времена электроники. Чрезмерное ожидание, процветающее в академическом и техническом мире, заразило общую литературу этого времени. Опасение, что эффект мыслящей машины отразится на человеке все время подогревалось писателями, в частности, серия книг Азимова про роботов показала последствия на моральных ценностях человека, в случае возможности интеллектуальных роботов выполнять функции человека.
Эти опасения, объединенные с невыполненными обещаниями, вызвали множество разочарований специалистов, подвергших критике исследования нейронных мереж. Результатом было прекращение финансирования. Период спада продолжался до 80-х годов.
1982 г. - к возрождению интереса привело несколько событий. Джон Хопфилд (John Hopfield) представил статью в национальную Академию Наук США. Подход Хопфилда показал возможности моделирования нейронных сетей на принципе новой архитектуры.
В то же время в Киото (Япония) состоялась Объединенная американо-японская конференция по нейронным сетям, которые объявили достижением пятой генерации. Американские периодические издания подняли эту историю, акцентируя, что США могут остаться позади, что привело к росту финансирования в области нейросетей.
С 1985 г. Американский Институт Физики начал ежегодные встречи - Нейронные сети для вычислений.
1989 г. - на встрече Нейронные сети для обороны Бернард Видров сообщил аудитории о начале четвертой мировой войны, где полем боя являются мировые рынки и производства.
1990 г. - Департамент программ инновационных исследований защиты малого бизнеса назвал 16 основных и 13 дополнительных тем, где возможно использование нейронных мереж.
Сегодня, обсуждение нейронных сетей происходят везде. Перспектива их использования кажется довольно яркой, в свете решения нетрадиционных проблем и является ключом к целой технологии. На данное время большинство разработок нейронных мереж принципиально работающие, но могут существовать процессорные ограничения. Исследования направлены на программные и аппаратные реализации нейросетей. Компании работают над созданием трех типов нейрочипов: цифровых, аналоговых и оптических, которые обещают быть волной близкого будущего.
Аналогия с мозгом
Точная работа мозга человека - все еще тайна. Тем не менее, некоторые аспекты этого удивительного процессора известны. Базовым элементом мозга человека являются специфические клетки, известные как нейроны, способные запоминать, думать и применять предыдущий опыт к каждому действию, что отличает их от остальных клеток тела.
Кора головного мозга человека является плоской, образованной из нейронов поверхностью, толщиной от 2 до 3 мм площадью около 2200 см2 , что вдвое превышает площадь поверхности стандартной клавиатуры. Кора главного мозга содержит около 1011 нейронов, что приблизительно равно числу звезд Млечного пути. Каждый нейрон связан с 103 - 104 другими нейронами. В целом мозг человека имеет приблизительно от 1014 до 1015 взаимосвязей.
Сила человеческого ума зависит от числа базовых компонент, многообразия соединений между ними, а также от генетического программирования и обучения.
Индивидуальный нейрон является сложным, имеет свои составляющие, подсистемы и механизмы управления и передает информацию через большое количество электрохимических связей. Насчитывают около сотни разных классов нейронов. Вместе нейроны и соединения между ними формируют недвоичный, нестойкий и несинхронный процесс, отличающийся от процесса вычислений традиционных компьютеров. Искусственные нейросети моделируют лишь главнейшие элементы сложного мозга, вдохновляющие ученых и разработчиков к новым путям решения проблемы.
Биологический нейрон
Нейрон (нервная клетка) является особой биологической клеткой, которая обрабатывает информацию. Она состоит из тела клетки - сомы (soma), и двух типов внешних древовидных ответвлений: аксона (axon) и дендритов (dendrites). Тело клетки содержит ядро (nucleus), которое содержит информацию о наследственных свойствах нейрона, и плазму, обладающую молекулярными средствами для производства необходимых нейрону материалов. Нейрон получает сигналы (импульсы) от других нейронов через дендриты (приемники) и передает сигналы, сгенерированные телом клетки, вдоль аксона (передатчика), который в конце разветвляется на волокна (strands). На окончаниях волокон находятся синапсы (synapses)[3].
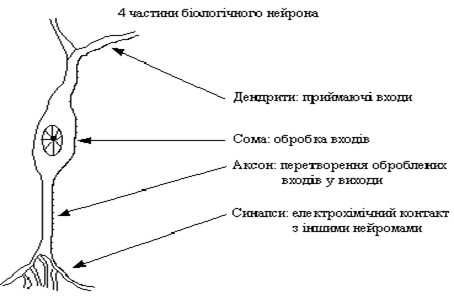
Рис.1 Биологический нейрон
Синапс является элементарной структурой и функциональным узлом между двумя нейронами (волокно аксона одного нейрона и дендрит другого). Когда импульс достигает синаптического окончания, высвобождаются определенные химические вещества, называемые нейротрансмиттерами. Нейротрансмиттеры проходят через синаптичную щель и, в зависимости от типа синапса, возбуждают или тормозят способность нейрона-приемника генерировать электрические импульсы. Результативность синапса настраивается проходящими через него сигналами, поэтому синапсы обучаются в зависимости от активности процессов, в которых они участвуют. Эта зависимость от предыстории действует как память, которая, возможно, отвечает за память человека. Нейроны способны запоминать, думать и применять предыдущий опыт к каждому действию, что отличает их от других клеток тела. Нейроны взаимодействуют с помощью короткой серии импульсов. Сообщение передается с помощью частотно-импульсной модуляции.
Последние экспериментальные исследования доказывают, что биологические нейроны структурно сложнее, чем упрощенное объяснение существующих искусственных нейронов, которые являются элементами современных искусственных нейронных сетей. Поскольку нейрофизиология предоставляет ученым расширенное понимание действия нейронов, а технология вычислений постоянно совершенствуется, разработчики сетей имеют неограниченное пространство для улучшения моделей биологического мозга.
Искусственный нейрон
История создания искусственных нейронов уходит своими корнями в 1943 год, когда шотландец МакКаллок и англичан Питтс создалитеорию формальных нейросетей, а через пятнадцать лет Розенблатт изобрёл искусственный нейрон (перцептрон), который впоследствии и лёг в основу нейрокомпьютера.
Несмотря на существенные различия, отдельные типы нейронных сетей обладают несколькими общими чертами.
Во-первых, основу каждой нейросети составляют относительно простые, в большинстве случаев – однотипные, элементы (ячейки), имитирующие работу нейронов мозга. Далее под нейроном будет подразумеваться искусственный нейрон, то есть ячейка нейросети. Каждый нейрон характеризуется своим текущим состоянием по аналогии с нервными клетками головного мозга, которые могут быть возбуждены или заторможены. Он обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон – выходную связь данного нейрона, с которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов. Общий вид нейрона приведен на рисунке 2. Каждый синапс характеризуется величиной синаптической связи или ее весом wi , который по физическому смыслу эквивалентен электрической проводимости.
|
Рис.2 Искусственный нейрон |
Текущее состояние нейрона определяется, как взвешенная сумма его входов:
(1)
Выход нейрона есть функция его состояния:
y = f(s) (2)
Нелинейная функция f называется активационной и может иметь различный вид, как показано на рисунке 3.
Одной из наиболее распространеных является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):
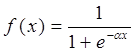(3)
При уменьшении a сигмоид становится более пологим, в пределе при a=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении a сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x=0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1]. Одно из ценных свойств сигмоидной функции – простое выражение для ее производной, применение которого будет рассмотрено в дальнейшем.
(4)
Следует отметить, что сигмоидная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Кроме того она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон.
Возвращаясь к общим чертам, присущим всем нейронным сетям, отметим, во-вторых, принцип параллельной обработки сигналов, который достигается путем объединения большого числа нейронов в так называемые слои и соединения определенным образом нейронов различных слоев, а также, в некоторых конфигурациях, и нейронов одного слоя между собой, причем обработка взаимодействия всех нейронов ведется послойно.
В качестве примера простейшей нейросети рассмотрим трехнейронный перцептрон (рис.4), то есть такую сеть, нейроны которой имеют активационную функцию в виде единичного скачка* . На n входов поступают некие сигналы, проходящие по синапсам на 3 нейрона, образующие единственный слой этой нейросети и выдающие три выходных сигнала:
, j=1...3 (5)
Очевидно, что все весовые коэффициенты синапсов одного слоя нейронов можно свести в матрицу W, в которой каждый элемент wij задает величину i-ой синаптической связи j-ого нейрона. Таким образом, процесс, происходящий в НС, может быть записан в матричной форме:
Y=F(XW) (6)
где X и Y – соответственно входной и выходной сигнальные векторы, F(V) – активационная функция, применяемая поэлементно к компонентам вектора V.
Теоретически число слоев и число нейронов в каждом слое может быть произвольным, однако фактически оно ограничено ресурсами компьютера или специализированной микросхемы, на которых обычно реализуется нейросеть. Чем сложнее нейронная сеть, тем масштабнее задачи, подвластные ей.
Выбор структуры нейросети осуществляется в соответствии с особенностями и сложностью задачи. Для решения некоторых отдельных типов задач уже существуют оптимальные, на сегодняшний день, конфигурации, описанные, например, в [2],[3],[4]. Если же задача не может быть сведена ни к одному из известных типов, разработчику приходится решать сложную проблему синтеза новой конфигурации. При этом он руководствуется несколькими основополагающими принципами: возможности сети возрастают с увеличением числа ячеек и плотности связей между ними и числом выделенных слоев; введение обратных связей наряду с увеличением возможностей сети поднимает вопрос о ее динамической устойчивости; сложность алгоритмов функционирования сети (в том числе, например, введение нескольких типов синапсов – возбуждающих, тормозящих и др.) также способствует усилению мощи нейросети. Вопрос о необходимых и достаточных свойствах сети для решения того или иного рода задач представляет собой целое направление нейрокомпьютерной науки. Так как проблема синтеза нейронной сети сильно зависит от решаемой задачи, дать общие подробные рекомендации затруднительно. В большинстве случаев оптимальный вариант получается на основе интуитивного подбора.
Очевидно, что процесс функционирования нейросети, то есть сущность действий, которые она способна выполнять, зависит от величин синаптических связей, поэтому, задавшись определенной структурой, отвечающей какой-либо задаче, разработчик сети должен найти оптимальные значения всех переменных весовых коэффициентов (некоторые синаптические связи могут быть постоянными).
Этот этап называется обучением нейросети, и от того, насколько качественно он будет выполнен, зависит способность сети решать поставленные перед ней проблемы во время эксплуатации. На этапе обучения кроме параметра качества подбора весов важную роль играет время обучения. Как правило, эти два параметра связаны обратной зависимостью и их приходится выбирать на основе компромисса.
Обучение нейронной сети может вестись с учителем или без него. В первом случае сети предъявляются значения как входных, так и желательных выходных сигналов, и она по некоторому внутреннему алгоритму подстраивает веса своих синаптических связей. Во втором случае выходы нейросети формируются самостоятельно, а веса изменяются по алгоритму, учитывающему только входные и производные от них сигналы.
Существует великое множество различных алгоритмов обучения, которые делятся на два больших класса: детерминистские и стохастические. В первом из них подстройка весов представляет собой жесткую последовательность действий, во втором – она производится на основе действий, подчиняющихся некоторому случайному процессу.
Развивая дальше вопрос о возможной классификации нейронных сетей, важно отметить существование бинарных и аналоговых сетей. Первые из них оперируют с двоичными сигналами, и выход каждого нейрона может принимать только два значения: логический ноль (заторможенное состояние) и логическая единица (возбужденное состояние). К этому классу сетей относится и рассмотренный выше перцептрон, так как выходы его нейронов, формируемые функцией единичного скачка, равны либо 0, либо 1. В аналоговых сетях выходные значения нейронов способны принимать непрерывные значения, что могло бы иметь место после замены активационной функции нейронов перцептрона на сигмоид.
Еще одна классификация делит нейронные сети на синхронные и асинхронные[3]. В первом случае в каждый момент времени свое состояние меняет лишь один нейрон. Во втором – состояние меняется сразу у целой группы нейронов, как правило, у всего слоя. Алгоритмически ход времени в нейросети задается итерационным выполнением однотипных действий над нейронами. Далее будут рассматриваться только синхронные нейронные сети.
Сети также можно классифицировать по числу слоев. На рисунке 5 представлен двухслойный перцептрон, полученный из перцептрона с рисунка 3 путем добавления второго слоя, состоящего из двух нейронов. Здесь уместно отметить важную роль нелинейности активационной функции, так как, если бы она не обладала данным свойством или не входила в алгоритм работы каждого нейрона, результат функционирования любой p-слойной нейросети с весовыми матрицами W(i) , i=1,2,...p для каждого слоя i сводился бы к перемножению входного вектора сигналов X на матрицу
W( S ) =W(1) W(2) ...W(p) (7)
то есть фактически такая p-слойная нейросеть эквивалентна однослойной сети с весовой матрицей единственного слоя W( S ) :
Y=XW( S ) (8)
Продолжая разговор о нелинейности, можно отметить, что она иногда вводится и в синаптические связи. Большинство известных на сегодняшний день сетей используют для нахождения взвешенной суммы входов нейрона формулу (1), однако в некоторых приложениях полезно ввести другую запись, например:
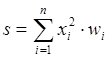(9)
или даже
(10)
Вопрос в том, чтобы разработчик нейросети четко понимал, для чего он это делает, какими ценными свойствами он тем самым дополнительно наделяет нейрон, и каких лишает. Введение такого рода нелинейности, вообще говоря, увеличивает вычислительную мощь сети, то есть позволяет из меньшего числа нейронов с нелинейными синапсами сконструировать нейронную сеть, выполняющую работу обычной сети с большим числом стандартных нейронов и более сложной конфигурации[1].
Многообразие существующих структур сетей позволяет отыскать и другие критерии для их классификации, но они выходят за рамки данной работы.
Теперь рассмотрим один нюанс, преднамеренно опущенный ранее. Из рисунка функции единичного скачка видно, что пороговое значение T, в общем случае, может принимать произвольное значение. Более того, оно должно принимать некое произвольное, неизвестное заранее значение, которое подбирается на стадии обучения вместе с весовыми коэффициентами. То же самое относится и к центральной точке сигмоидной зависимости, которая может сдвигаться вправо или влево по оси X, а также и ко всем другим активационным функциям. Это, однако, не отражено в формуле (1), которая должна была бы выглядеть так:
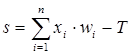(11)
Дело в том, что такое смещение обычно вводится путем добавления к слою нейронов еще одного входа, возбуждающего дополнительный синапс каждого из нейронов, значение которого всегда равняется 1. Присвоим этому входу номер 0. Тогда
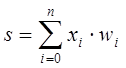, (12)
где w0 = –T, x0 = 1.
Очевидно, что различие формул (1) и (12) состоит лишь в способе нумерации входов.
Из всех активационных функций, изображенных на рисунке 3, одна выделяется особо. Это гиперболический тангенс, зависимость которого симметрична относительно оси X и лежит в диапазоне [-1,1]. Выбор области возможных значений выходов нейронов во многом зависит от конкретного типа сети и является вопросом реализации, так как манипуляции с ней влияют на различные показатели эффективности сети, зачастую не изменяя общую логику ее работы.
Обучение искусственных нейронных сетей
Обучить нейронную сеть - значит, сообщить ей, чего мы от нее добиваемся. Этот процесс очень похож на обучение ребенка алфавиту. Показав ребенку изображение буквы А, мы спрашиваем его: Какая это буква? Если ответ неверен, мы сообщаем ребенку тот ответ, который мы хотели бы от него получить: Это буква А. Ребенок запоминает этот пример вместе с верным ответом, то есть в его памяти происходят некоторые изменения в нужном направлении. Мы будем повторять процесс предъявления букв снова и снова до тех пор, когда все 33 буквы будут твердо запомнены. Такой процесс называют обучение с учителем.
При обучении нейронной сети мы действуем совершенно аналогично. У нас имеется некоторая база данных, содержащая примеры (набор рукописных изображений букв). Предъявляя изображение буквы А на вход нейронной сети, мы получаем от нее некоторый ответ, не обязательно верный. Нам известен и верный (желаемый) ответ - в данном случае нам хотелось бы, чтобы на выходе нейронной сети с меткой А уровень сигнала был максимален. Обычно в качестве желаемого выхода в задаче классификации берут набор (1, 0, 0, ...), где 1 стоит на выходе с меткой А, а 0 - на всех остальных выходах. Вычисляя разность между желаемым ответом и реальным ответом сети, мы получаем 33 числа - вектор ошибки. Алгоритм обратного распространения ошибки - это набор формул, который позволяет по вектору ошибки вычислить требуемые поправки для весов нейронной сети. Одну и ту же букву (а также различные изображения одной и той же буквы) мы можем предъявлять нейронной сети много раз. В этом смысле обучение скорее напоминает повторение упражнений в спорте - тренировку.
Оказывается, что после многократного предъявления примеров веса нейронной сети стабилизируются, причем нейронная сеть дает правильные ответы на все (или почти все) примеры из базы данных. В таком случае говорят, что нейронная сеть выучила все примеры, нейронная сеть обучена, или нейронная сеть натренирована. В программных реализациях можно видеть, что в процессе обучения величина ошибки (сумма квадратов ошибок по всем выходам) постепенно уменьшается. Когда величина ошибки достигает нуля или приемлемого малого уровня, тренировку останавливают, а полученную нейронную сеть считают натренированной и готовой к применению на новых данных.
Важно отметить, что вся информация, которую нейронная сеть имеет о задаче, содержится в наборе примеров. Поэтому качество обучения нейронной сети напрямую зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описывают данную задачу. Так, например, бессмысленно использовать нейронную сеть для предсказания финансового кризиса, если в обучающей выборке кризисов не представлено. Считается, что для полноценной тренировки нейронной сети требуется хотя бы несколько десятков (а лучше сотен) примеров.
Повторим еще раз, что обучение нейронных сетей - сложный и наукоемкий процесс. Алгоритмы обучения нейронных сетей имеют различные параметры и настройки, для управления которыми требуется понимание их влияния.
Применение нейронных сетей
После того, как нейронная сеть обучена, мы можем применять ее для решения полезных задач. Важнейшая особенность человеческого мозга состоит в том, что, однажды обучившись определенному процессу, он может верно, действовать и в тех ситуациях, в которых он не бывал в процессе обучения. Например, мы можем читать почти любой почерк, даже если видим его первый раз в жизни. Так же и нейронная сеть, грамотным образом обученная, может с большой вероятностью правильно реагировать на новые, не предъявленные ей ранее данные. Например, мы можем нарисовать букву А другим почерком, а затем предложить нашей нейронной сети классифицировать новое изображение. Веса обученной нейронной сети хранят достаточно много информации о сходстве и различиях букв, поэтому можно рассчитывать на правильный ответ и для нового варианта изображения.
Список литературы
1 http://www.module.ru/files/un_neuron_net.pdf
2 http://www.neuroproject.ru/neuro.htm
3 http://www.orc.ru/~stasson/neurox.html#articles
цикл статей: «нейронные сети: основные положения», C.Короткий
4 http://mechanoid.narod.ru/nns/base
Основные модели и методы теории искусственных нейронных сетей, Борисов Е. С., 19 октября 2005 г.
* Иногда перцептроном называют любую НС слоистой структуры, однако здесь и далее под перцептроном понимается только сеть, состоящая из нейронов с активационными функциями единичного скачка (бинарная сеть).