Обработка многократных измерений
СОДЕРЖАНИЕ: Введение Измерения — один из важнейших путей познания природы человеком. Они играют огромную роль в современном обществе. Наука и промышленность не могут существовать без измерений. Практически нет ни одной сферы деятельности человека, где бы интенсивно не использовались результаты измерений, испытаний и контроля.Введение
Измерения — один из важнейших путей познания природы человеком. Они играют огромную роль в современном обществе. Наука и промышленность не могут существовать без измерений. Практически нет ни одной сферы деятельности человека, где бы интенсивно не использовались результаты измерений, испытаний и контроля.
Диапазон измерительных величин и их количество постоянно растут и поэтому возрастает и сложность измерений. Они перестают быть одноактным действием и превращаются в сложную процедуру подготовки и проведения измерительного эксперимента и обработки полученной информации.
Другой причиной важности измерений является их значимость. Основа любой формы управления, анализа, прогнозирования, контроля или регулирования — достоверная исходная информация, которая может быть получена лишь путем измерения требуемых физических величин, параметров и показателей. Только высокая и гарантированная точность результатов измерений обеспечивает правильность принимаемых решений.
Методической основой стандартизации являются математические методы, включая предпочтительные числа и ряды предпочтительных чисел, параметрические ряды, а также унификация деталей и узлов, агрегатирование, комплексная и опережающая стандартизация.
Предпочтительные числа и ряды предпочтительных чисел необходимы для выбора оптимального ряда параметров и типоразмеров готовых изделий. Набор установленных значений параметров составляет параметрический ряд, который строится по системе предпочтительных чисел.
1. Обработка результатов многократных измерений:
Систематическая погрешность (0,25)%
Доверительная вероятность 0,1%
Результаты измерений: 99,72; 100,71; 91,55; 96,02; 97,68; 93,04; 92,84; 93,14; 97,31; 94,7; 90,24; 92,15; 96,02; 100,13; 94,51; 94,6; 93,01; 97,47; 96,54; 94,96; 96,29; 99,63; 94,16.
Обработка многократных измерений
Предполагаем, что измерения равноточные, т.е. выполняются одним экспериментатором, в одинаковых условиях, одним прибором. Методика сводится к следующему: проводят n наблюдений (единичных измерений) и фиксируют n результатов измерений одного и того же значения физической величины.
1) Исключаем известные систематические погрешности результатов измерений и получаем исправленный результат 
;
= 
(1- /100),
где =0,25 % - систематическая погрешность.
= (1-0.25/100)
=
0.9975
= 99,74 0.9975; = 99,4707
=100,71 0.9975; 
=100,4582
=91,55 0.9975; 
=91,32113
=96,02 0.9975; 
=95,77995
=97,68 0.9975; =97,4358
=93,04 0.9975; 
=92,8074
=92,84 0.9975; 
=92,6079
=93,14 0.9975; 
=92,90715
=97,31 0.9975; 
=97,06673
=94,7 0.9975; 
=94,46325
=90,24 0.9975; 
=90,0144
=92,15 0.9975; 
=91,91963
=96,02 0.9975; 
=95,77995
=100,13 0.9975; 
=99,87968
=94,51 0.9975; 
=94,27373
=94,6 0.9975; 
=94,3635
=93,01 0.9975; 
=92,77748
=97,47 0.9975; 
=97,22633
=96,54 0.9975; 
=96,29865
=94,96 0.9975; 
=94,7226
=96, 29 0.9975; 
=96,04928
=99, 63 0.9975; 
=99,38093
=94, 16 0.9975; 
=93,9246
=2190,928
2) Находим среднее арифметическое значение исправленных результатов и принимают его за результат измерений
;
n=23
=
2190,928
=95,2577
3) Вычисляем оценку среднеквадратического отклонения результата измереий.
а) находим отклонения от среднего арифметического 
;
= 95,2577-99,4707 =-4,213
=95,2577-100,4582 =-5,201
=95,2577-91,32113 =3,938
=95,2577-95,77995 =-0,522
=95,2577-97,4358 =-2,178
=95,2577-92,8074 =2,450
=95,2577-92,6079 =2,650
=95,2577-92,90715 =2,351
=95,2577-97,06673 =-1,809
=95,2577-94,46325 =0,795
=95,2577-90,0144 =5,243
95,2577-91,91963 
=3,338
95,2577-95,77995 
=-0,522
=95,2577-99,87968 =-4,622
95,2577-94,27373 
=0,984
95,2577-94,3635 
=0,894
=95,2577-92,77748 =2,481
=95,2577-97,22633 =-1,968
=95,2577-96,29865 =-1,040
95,2577-94,7226 
=0,535
95,2577-96,04928 
=-0,794
95,2577-99,38093 
=-4,123
=95,2577-93,9246 
=1,333
=0
б) проверили правильность вычислений, и они верны,
т.к.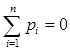 
;
в) вычисляем квадраты отклонений от среднего 
;
=17,749
=27,05
=15,507
=0,272
=4,744
=6,003
=7,025
=5,527
=3,72
=0,632
=27,458
=11,142
=0,272
=21,363
=0,968
=0,799
=6,155
=3,873
=1,082
=0,286
=0,630
=16,999
=1,777
=181,033
г) определяем оценку среднеквадратического отклонения
;
=
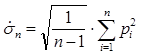181,033
0.21181,033
=38,0169
д) находим значение относительной среднеквадратической случайной погрешности
;
=
=0,399
4) Вычисляем оценку среднеквадратического отклонения результата измерения
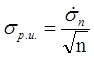; n=23
=
= 
= 7.9268
5) Вычисляем доверительные границы случайной погрешности результатов измерений:
а) задаются коэффициентом доверия 
(доверительной вероятности);
=0.1%
б) по специальным таблицам определяют значение коэффициента Стьюдента (
), соответствующее заданной доверительной вероятности и числу наблюдений;
где, n – число наблюдений;
– доверительная вероятность
n=23
=0.1%
t=1.319460
в) находим значение 
;
t=1.319460
=7.9268
1.3194607.9268
=10,4591
г) вычисляем доверительные границы 
и 
.
=95,2577
=10,4591
95,2577-10,4591=84.7986
95,2577+10,4591=105.7168
6) записываем результат измерений.
84.7986
x 105.7168
2. Система предпочтительных чисел в стандартизации
Определить ряд по заданной последовательности чисел 1,6; 1,8; 2,0; 2,2; 2,4; 2,7
1. По определению знаменателя ряда находим его значение как отношение соседних чисел ряда (как среднее арифметическое):
=1.6; 
=1.8; 
=2.0;
=2.2; 
=2.4; 
=2.7
- член прогрессии, принятый за начальный.
=
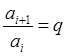
=1,13
=
=1,11
=
=1,1
=
=1,1
=
=1,13
=5.57
=
; n=5
=
=1.11
, что соответствует ряду E24
2. Вычисленное число 
близко расположено к 
= 1,10. Это соответствует ряду по ГОСТу: Е24.
=
Записать в развернутом виде ряд R10/2 (0,125...2000)
а). Записали ряд в развернутом виде: R10/2 (0,125; 0,2; 0,315; 0,5; 0,8; 1,25; 2,0; 3,15; 5,0; 8,0; 12,5; 20,0; 31,5; 50; 80; 125; 200; 315; 500; 800; 1250; 2000.)
б). Подсчитали число значений ряда.
- член прогрессии, принятый за начальный.
=0,125; 
=0,2; 
=0,315;= 0,5; =0,8; =1,25; 
=2,0;
=3,15; 
=5,0; 
=8,0; 
=12,5; 
=20,0;
= 31,5; 
=50;
= 80; 
=125;
= 200; 
=315; 
=500; 
=800;
= 1250; 
=2000.
число значений ряда n=22
в) Определили знаменатель ряда.
=
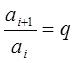
=1,6
= 
=1,58
= 
=1,59
=
=1,6
=
=1,56
=
=1,6
=
=1,58
=
=1,59
=
=1,6
= 
=1,56
= 
=1,6
=
=1,58
=
=1,59
=
=1,6
=
=1,56
=
=1,6
=
=1,58
=
=1,59
=
=1,6
= 
=1,56
=
=1,6
,n=21
=
=
=1.59
г) Вычислили номера предпочтительных чисел.
Порядковые номера чисел представляют собой основание ряда, умноженное на десятичный логарифм числа ряда.
R - число значений ПЧ в десятичном интервале (номер ряда).
=10
;
= -9
=10
;
= -7
=10
=-5
=10
=-3
=10
=-1
=10
=1
=10
;
=3
=10
=5
=10
; =7
=10
=9
=10
=11
=10
;
=13
=10
;
=15
=10
=17
=10
=19
=10
; =21
=10
; =23
=10
=25
=10
=27
=10
=29
=10
;
=31
=10
; =33
Найти номер ПЧ можно еще одним способом:
где i0 - номер числа в нулевом интервале
k - целое положительное или отрицательное число, определяющее удаление рассматриваемого интервала в ту или другую сторону от нулевого;
R - число значений ПЧ в десятичном интервале (номер ряда).
По таблице ПЧ находим числа в нулевом интервале i0 и, тогда из формулы имеем:
РядR10
k=-1 ; =1-1
10; =-9
k=-1; =3-110;=-7
k=-1;
=5-110;
=-5
k=-1; =7-110;
=-3
k=-1; =9-110;
=-1
k=0; 
=1-010;
=1
k=0; =3-010;=3
k=0; =5-010; ; 
5
k=0; =7-010;
=7
k=0; =9-010; =9
k=1; 
=1+110; 
11
k=1; =3+110; =13
k=1; =5+110; 
15
k=1; =7+110; =17
k=1; =9+110; =19
k=2; =1+210; 
21
k=2; =3+210; =23
k=2; =5+210; =25
k=2; =7+210; =27
k=2; =9+210; =29
k=3; 
=1+310; 
31
k=3; =3+310; =33
Записать в развернутом виде ряд Е12/3 (0,00027...0,015) Е6/2 (0,001...2,2)
а).Записали ряд в развернутом виде
Е12/3 (0,00027...0,001);
Е12/3(0,00027;0,00047;0,00082.)
Е6/2 (0,001...2,2)
Е6/2(0,001;0,0022;0,0047;0,010;0,022;0,047;0,1;0,22;0,47;1;2,2;)
б).Определили знаменатели рядов. Е12/3
=0.00027;
=0,00047;
=0,00082.
- член прогрессии, принятый за начальный.
=
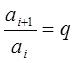
=1,7;
=
= 1,7;
=
= 1,8;
 |
= 5,2; n=3
=
=
5,2
1,73
Знаменатель ряда Е12/3 (0,00027...0,015)
1,73
Е 6/2
=0,001;
=0,0022;
=0,0047;
=0,01;
=0,022;
=0,047;
=0,1
=0,22; =0,47;
=1;
=2,2.
- член прогрессии, принятый за начальный.
=
= 2,2
=
= 2,1
=
= 2,1
=
= 2,2
=
= 2,1
=
= 2,1
=
= 2,2
=
= 2,1
=
= 2,1
=
= 2,2
=21,40
=
=
21,40 
Знаменатель ряда Е6/2 (0,001...2,2)
Заключение
Многократные измерения - измерения, при которых число измерений превышает число измеряемых величин в n/m раз, где n - число измерений каждой величины, m - число измеряемых величин. Обычно для многократных измерений принято n или = 3. Многократные измерения проводят с целью уменьшения влияния случайных составляющих погрешностей измерения.
Применение рядов предпочтительных чисел представляет собой параметрическую стандартизацию, которая позволяет получить значительный эффект на всех стадиях жизненного цикла изделий ( проектирование, изготовление, эксплуатация и др.) Стандартами параметров охватывается большой диапазон характеристик изделий: материалы, заготовки, размерный режущий инструмент, оснастка, контрольные калибры, узлы по присоединительным размерам, выходные параметры электродвигателей и многое другое, что используется в той или иной отрасли промышленности.
Список использованных источников
1. Шишкин И.Ф. Метрология, стандартизация и управление качеством – М.: Изд-во стандартов, 1990.
2. Ю. Димов. Метрология, стандартизация и сертификация: Учебник для вузов. 2-е изд. 2004 г432 стр.
3. Алексеев В.В., Авдеев Б.Я., Антонюк Е.М. Метрология, стандартизация и сертификация .1- е изд.: ООО Аргумент, Изд. Академия/Academia, 2007 г. 384 стр.
4. В.В. Алексеева. Метрология, стандартизация и сертификация: Учебник для студентов высших учебных заведений.2-е изд., стер. Изд.: Академия ИЦ 2008г.379стр.
ПРИЛОЖЕНИЕ
Распределение Стьюдента (t-критерий
| n/ | 0.40 | 0.25 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.0005 |
| 1 | 0.324920 | 1.000000 | 3.077684 | 6.313752 | 12.70620 | 31.82052 | 63.65674 | 636.6192 |
| 2 | 0.288675 | 0.816497 | 1.885618 | 2.919986 | 4.30265 | 6.96456 | 9.92484 | 31.5991 |
| 3 | 0.276671 | 0.764892 | 1.637744 | 2.353363 | 3.18245 | 4.54070 | 5.84091 | 12.9240 |
| 4 | 0.270722 | 0.740697 | 1.533206 | 2.131847 | 2.77645 | 3.74695 | 4.60409 | 8.6103 |
| 5 | 0.267181 | 0.726687 | 1.475884 | 2.015048 | 2.57058 | 3.36493 | 4.03214 | 6.8688 |
| 6 | 0.264835 | 0.717558 | 1.439756 | 1.943180 | 2.44691 | 3.14267 | 3.70743 | 5.9588 |
| 7 | 0.263167 | 0.711142 | 1.414924 | 1.894579 | 2.36462 | 2.99795 | 3.49948 | 5.4079 |
| 8 | 0.261921 | 0.706387 | 1.396815 | 1.859548 | 2.30600 | 2.89646 | 3.35539 | 5.0413 |
| 9 | 0.260955 | 0.702722 | 1.383029 | 1.833113 | 2.26216 | 2.82144 | 3.24984 | 4.7809 |
| 10 | 0.260185 | 0.699812 | 1.372184 | 1.812461 | 2.22814 | 2.76377 | 3.16927 | 4.5869 |
| 11 | 0.259556 | 0.697445 | 1.363430 | 1.795885 | 2.20099 | 2.71808 | 3.10581 | 4.4370 |
| 12 | 0.259033 | 0.695483 | 1.356217 | 1.782288 | 2.17881 | 2.68100 | 3.05454 | 4.3178 |
| 13 | 0.258591 | 0.693829 | 1.350171 | 1.770933 | 2.16037 | 2.65031 | 3.01228 | 4.2208 |
| 14 | 0.258213 | 0.692417 | 1.345030 | 1.761310 | 2.14479 | 2.62449 | 2.97684 | 4.1405 |
| 15 | 0.257885 | 0.691197 | 1.340606 | 1.753050 | 2.13145 | 2.60248 | 2.94671 | 4.0728 |
| 16 | 0.257599 | 0.690132 | 1.336757 | 1.745884 | 2.11991 | 2.58349 | 2.92078 | 4.0150 |
| 17 | 0.257347 | 0.689195 | 1.333379 | 1.739607 | 2.10982 | 2.56693 | 2.89823 | 3.9651 |
| 18 | 0.257123 | 0.688364 | 1.330391 | 1.734064 | 2.10092 | 2.55238 | 2.87844 | 3.9216 |
| 19 | 0.256923 | 0.687621 | 1.327728 | 1.729133 | 2.09302 | 2.53948 | 2.86093 | 3.8834 |
| 20 | 0.256743 | 0.686954 | 1.325341 | 1.724718 | 2.08596 | 2.52798 | 2.84534 | 3.8495 |
| 21 | 0.256580 | 0.686352 | 1.323188 | 1.720743 | 2.07961 | 2.51765 | 2.83136 | 3.8193 |
| 22 | 0.256432 | 0.685805 | 1.321237 | 1.717144 | 2.07387 | 2.50832 | 2.81876 | 3.7921 |
| 23 | 0.256297 | 0.685306 | 1.319460 | 1.713872 | 2.06866 | 2.49987 | 2.80734 | 3.7676 |
| 24 | 0.256173 | 0.684850 | 1.317836 | 1.710882 | 2.06390 | 2.49216 | 2.79694 | 3.7454 |
| 25 | 0.256060 | 0.684430 | 1.316345 | 1.708141 | 2.05954 | 2.48511 | 2.78744 | 3.7251 |
| 26 | 0.255955 | 0.684043 | 1.314972 | 1.705618 | 2.05553 | 2.47863 | 2.77871 | 3.7066 |
| 27 | 0.255858 | 0.683685 | 1.313703 | 1.703288 | 2.05183 | 2.47266 | 2.77068 | 3.6896 |
| 28 | 0.255768 | 0.683353 | 1.312527 | 1.701131 | 2.04841 | 2.46714 | 2.76326 | 3.6739 |
| 29 | 0.255684 | 0.683044 | 1.311434 | 1.699127 | 2.04523 | 2.46202 | 2.75639 | 3.6594 |
| 30 | 0.255605 | 0.682756 | 1.310415 | 1.697261 | 2.04227 | 2.45726 | 2.75000 | 3.6460 |
| inf | 0.253347 | 0.674490 | 1.281552 | 1.644854 | 1.95996 | 2.32635 | 2.57583 | 3.2905 |
Согласно приведенной таблице:
1) n – число наблюдений;
2) – доверительная вероятность.
Предпочтительные числа рядов R5, R10, R20, R40
| № числа | Предп. числа | № числа | Предп. числа | № числа | Предп. числа | № числа | Предп. числа | № числа | Предп. числа |
| 0 | 1,00 | - | - | - | - | - | - | - | - |
| 1 | 1,06 | 9 | 1,70 | 17 | 2,65 | 25 | 4,25 | 33 | 6,70 |
| 2 | 1,12 | 10 | 1,80 | 18 | 2,80 | 26 | 4,50 | 34 | 7,10 |
| 3 | 1,18 | 11 | 1,90 | 19 | 3,00 | 27 | 4,75 | 35 | 7,50 |
| 4 | 1,25 | 12 | 2,00 | 20 | 3,15 | 28 | 5,00 | 36 | 8,00 |
| 5 | 1,32 | 13 | 2,12 | 21 | 3,35 | 29 | 5,30 | 37 | 8,50 |
| 6 | 1,40 | 14 | 2,24 | 22 | 3,55 | 30 | 5,60 | 38 | 9,00 |
| 7 | 1,50 | 15 | 2,36 | 23 | 3,75 | 31 | 6,00 | 39 | 9,50 |
| 8 | 1,60 | 16 | 2,50 | 24 | 4,00 | 32 | 6,30 | 40 | 10,00 |
Ряду R5 соответствует нижняя строка таблицы, ряду R10 – пятая и нижняя, ряду R20 – строки 3, 5, 7, 9 и ряду R40 – вся таблица.
Предпочтительные числа рядов Е3, Е6, Е12, Е24
| 1,0 | - | - | - | - | - |
| 1,1 | 1,6 | 2,4 | 3,6 | 5,1 | 7,5 |
| 1,2 | 1,8 | 2,7 | 3,9 | 5,6 | 8,2 |
| 1,3 | 2,0 | 3,0 | 4,3 | 6,2 | 9,1 |
| 1,5 | 2,2 | 3,3 | 4,7 | 6,8 | 10,0 |
Ряду Е3 соответствуют числа 2,2; 4,7; 10. Ряду E6 соответствует нижняя строка, ряду E12 – третья и пятая, а ряду E24 – вся таблица.
Знаменатели рядов предпочтительных чисел
Условные обозначения |
Знаменатель ряда, q | Количество членов в десятичном интервале | |
| Точное значение | Округленное значение | ||
| R5 |  |
1,60 | 5 |
| R10 |   |
1,25 | 10 |
| R20 |  |
1,12 | 20 |
| R40 |  |
1,06 | 40 |
| R80 |  |
1,03 | 80 |
| R160 |  |
1,015 | 160 |
| E3 |  |
2,20 | 3 |
| E6 |  |
1,50 | 6 |
| E12 |  |
1,20 | 12 |
| E24 |  |
1,10 | 24 |
| E48 |  |
1,05 | 48 |
| E96 |  |
1,025 | 96 |
| E192 |  |
1,012 | 192 |