Обробка результатів прямих багатократних рівноточних статистичних вимірювань
СОДЕРЖАНИЕ: Національний університет «Львівська політехніка» Кафедра телекомунікацій Метрологія Обробка результатів прямих багатократних рівноточних (статистичних) вимірюваньНаціональний університет «Львівська політехніка»
Кафедра телекомунікацій
Метрологія
Обробка результатів прямих багатократних рівноточних (статистичних) вимірювань
Виконав :
студент групи ТК-31
ІТРЕ, НУ «ЛП»
Перевірив :
викладач з метрології
ЛЬВІВ 2006
Тема. Обробка результатів прямих багатократних рівноточних (статистичних) вимірювань.
Мета: вивчення стандартної методики обробки результатів статистичних вимірювань, а також вивчення способів представлення результатів таких вимірювань.
Початкові дані та схема вимірювання.
|
|
Початкові дані:
Номінальне значення частоти: 520 Гц
Точність установки частоти генератора: ![]() %
%
Початковий статистичний ряд результатів вимірювань:
Початкова таблиця даних вимірювань :
№ дослідження Значення частоти
| 1 | 707,292 |
| 2 | 705,765 |
| 3 | 707,603 |
| 4 | 707,749 |
| 5 | 708,273 |
| 6 | 707,518 |
| 7 | 707,425 |
| 8 | 707,309 |
| 9 | 709,235 |
| 10 | 708,987 |
| 11 | 707,751 |
| 12 | 707,075 |
| 13 | 709,744 |
| 14 | 707,739 |
| 15 | 707,782 |
| 16 | 707,338 |
| 17 | 707,780 |
| 18 | 708,002 |
| 19 | 705,765 |
| 20 | 707,182 |
| 21 | 705,781 |
| 22 | 707,656 |
| 23 | 707,763 |
| 24 | 707,497 |
| 25 | 707,991 |
| 26 | 707,257 |
| 27 | 707,177 |
| 28 | 705,781 |
| 29 | 706,730 |
| 30 | 707,385 |
| 31 | 707,538 |
| 32 | 706,729 |
| 33 | 707,787 |
| 34 | 707,424 |
| 35 | 706,415 |
№ аі
аі
-![]() (аі
-
(аі
-![]() )
)
| 1 | 707,292 | -0,143 | 0,020 |
| 2 | 705,765 | -1,670 | 2,789 |
| 3 | 707,603 | 0,168 | 0,028 |
| 4 | 707,749 | 0,314 | 0,099 |
| 5 | 708,273 | 0,838 | 0,702 |
| 6 | 707,518 | 0,083 | 0,007 |
| 7 | 707,425 | -0,010 | 0,000 |
| 8 | 707,309 | -0,126 | 0,016 |
| 9 | 709,235 | 1,800 | 3,240 |
| 10 | 708,987 | 1,552 | 2,409 |
| 11 | 707,751 | 0,316 | 0,100 |
| 12 | 707,075 | -0,360 | 0,130 |
| 13 | 709,744 | 2,309 | 5,331 |
| 14 | 707,739 | 0,304 | 0,092 |
| 15 | 707,782 | 0,347 | 0,120 |
| 16 | 707,338 | -0,097 | 0,009 |
| 17 | 707,780 | 0,345 | 0,119 |
| 18 | 708,002 | 0,567 | 0,321 |
| 19 | 705,765 | -1,670 | 2,789 |
| 20 | 707,182 | -0,253 | 0,064 |
| 21 | 705,781 | -1,654 | 2,736 |
| 22 | 707,656 | 0,221 | 0,049 |
| 23 | 707,763 | 0,328 | 0,108 |
| 24 | 707,497 | 0,062 | 0,004 |
| 25 | 707,991 | 0,556 | 0,309 |
| 26 | 707,257 | -0,178 | 0,032 |
| 27 | 707,177 | 0,258 | 0,067 |
| 28 | 705,781 | -1,654 | 2,736 |
| 29 | 706,730 | -0,705 | 0,497 |
| 30 | 707,385 | -0,050 | 0,002 |
| 31 | 707,538 | 0,103 | 0,011 |
| 32 | 706,729 | -0,706 | 0,498 |
| 33 | 707,787 | 0,352 | 0,124 |
| 34 | 707,424 | -0,011 | 0,000 |
| 35 | 706,415 | -1,020 | 1,040 |
Виявлення та відсіювання результатів вимірювань, які містять грубі похибки та промахи.
підраховуємо середнє значення ![]() :
:
 , де N=35 ;
, де N=35 ;
далі рахуємо відхилення кожного з вимірювань від середнього значення (аі
-![]() );
);
підносимо знайдені значення до квадрату(тобто знаходимо квадратичне відхилення), (аі
-![]() );
);
знаходимо середнє квадратичне відхилення :
![]()
і останній крок перед побудовою графіка є визначення верхньої та нижньої межі :
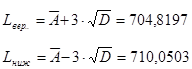
отже, будуємо графік :
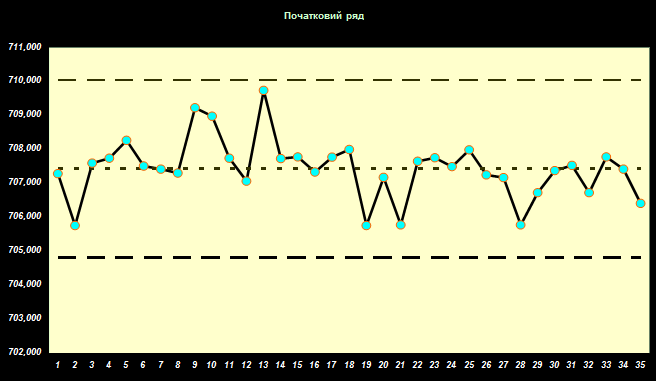
Як видно з графіка, статистичний ряд не містить грубих помилок, а отже є однорідним. Основними параметрами такого ряду є :
![]()
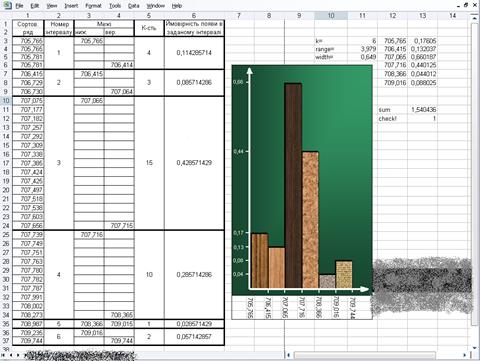
ІІІ. Побудова гістограми та визначення ймовірностей попадання в інтервал
Сортуємо ряд від найменшого значення до найбільшого, далі обраховуємо розмах значень
dF = Fmax – Fmin = 3,979
Кількість інтервалів на заданому проміжку :
K=1 + 3,322 * lg [35] = 6 [відповідь заокруглюємо до цілого числа]
Частотний діапазон одного інтервалу :
W = dF / K = 0,649
Визначаємо межі кожного з інтервалів :
Lниж.i= Fmin+(Ni-1)*W+0,001 Lниж.1 = Fmin
Lвер.і = Fmin +Ni*WLвер.6 = Fmax
Рахуємо кількість значень, що попали у кожен інтервал.
Обраховуємо тепер ймовірності попадання в кожен інтервалPi = Ni/N.
І на кінець будуємо гістограму, відкладаючи прямокутники шириною Wта висотою P/W, так щоб сума площ всіх прямокутників дорівнювала одиниці.