Общая Физика лекции по физике за II семестр СПбГЭТУ ЛЭТИ
СОДЕРЖАНИЕ: 1. Эл. поле в вакууме: Электрическое поле – проявление единого электромагнитного поля, проявлением которого является электрический ток (упорядоченное движение заряженных частиц).
1. Эл. поле в вакууме:
Электрическое поле – проявление единого электромагнитного поля, проявлением которого является электрический ток (упорядоченное движение заряженных частиц).
Эл. заряды – частицы с наименьшим отрицательным (электроны) или положительным (протоны) зарядом.
I -ый закон Кулона: суммарный эл. заряд в замкнутой системе остается постоянным.
II -й закон Кулона (о взаимодействии точечных зарядов):
Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними.
F12 = k*|q1q2|/r122
Где F12 – сила взаимодействия между двумя точечными зарядами;
k = 1/(4pe0e); e 1;
e - относительная электрическая проницаемость;
e0 = 8,85*10-12 Ф/м;
e0 =1/(4p*9*109 ).
Если зарядов будет N, то сила взаимодействия между двумя данными зарядами не изменится, то
F = F1i, i = 1 N.
2. Напряженность:
В качестве величины, характеризующей электрическое поле, принята величина E = F / qпр.
Ее называют напряженностью электрического поля в точке, где пробный заряд испытывает действие силы F.
Напряженность эл. поля в данной точке:
Е = (1/4pe0)*(q/r2 ), q – заряд, обуславливающий поле.
Вектор Е направлен вдоль радиальной прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателен.
За единицу напряженности принят В/м.
Принцип суперпозиции: напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности.
3. Законы Кулона:
I -ый закон Кулона: суммарный эл. заряд в замкнутой системе остается постоянным.
II -й закон Кулона (о взаимодействии точечных зарядов):
Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними.
F12 = k*|q1q2|/r122
Где F12 – сила взаимодействия между двумя точечными зарядами;
k = 1/(4pe0e); e 1;
e - относительная электрическая проницаемость;
e0 = 8,85*10-12 Ф/м;
e0 =1/(4p*9*109 ).
8. Линии напряженности:
Электрическое поле можно описать с помощью линий напряженности. Их проводят таким образом, чтобы касательная к ним в данной точке совпадала с направлением вектора Е.
Густота линий выбирается так, чтобы кол-во линий, пронизывающих единицу поверхности, было равно численному значению вектора Е. (1)
Линии напряженности точечного заряда представляют собой совокупность радиальных прямых, направленных от положительного заряда и к отрицательному.
Линии одним концом «опираются» на заряд, а другим концом уходят в бесконечность (2).
Так полное число линий, пересекающих сферическую поверхность радиуса r, будет равно произведению густоты линий на площадь поверхности сферы (4pr2 ). В соответствии с (1), густота линий численно равна Е = (1/4pe0)*(q/r2 ), то кол-во линий численно равно (1/4pe0)*(q/r2 )* (4pr2 ) = q/e0. Это говорит о том, что число линий на любом расстоянии от заряда будет постоянным, то, в соответствии с (2), получается, что линии ни где, кроме заряда, не начинаются и не заканчиваются.
5. Поле электрического диполя:
Электрическим диполем называется система двух одинаковых по величине разноименных зарядов +q и –q, расстояние l между которыми значительно меньше расстояния до точек, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя .
Положим, что r+ = r – a cos u, а r- = r + a cos u.
Спроецируем вектор Е на два взаимно перпендикулярных направления Er и Eu :
Er = 1/(4pe0 )*(2p. cosu)/r3 ;
Eu = 1/(4pe0 )*(p. sinu)/r3 , где p = q. l – характеристика диполя, называемая его электрическим моментом. Вектор р направлен по оси диполя от отрицательного заряда к положительному.
E2 = Er 2 + Eu 2 E = 1/(4pe0 )*p/r3 * *(1+3. cos2 u).
Если предположить, что u = p/2, то получим напряженность на прямой, проходящей через центр диполя и перпендикулярной к его оси:
E^ = 1/(4pe0 )* p/r3 , при этом Er = 0, то E^ параллелен оси диполя.
|
 |
|
|
|
|
|
![]()
 dr
dr
|
dE = k*(tdl)/L2
dE1 = dE. cosa = dE(x/4) = =k*t*(x. dl)/(R2 +x2 )3/2 2 p R
E1 = dE1 = k*t*(x. dl)/(R2 +x2 )3/2 0 dl = = (2pRtkx)/(R2 +x2 )3/2 = =k*(Q. x)/ (R2 +x2 )3/2 .
|
dr
|
|
|
|
|
|
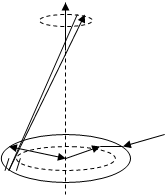
g - плотность распределения заряда
dQ = gdS = g2prdr
dE1 = k*(dQx)/(r2 +x2 )3/2 = =kg2p*(xrdr)/(r2 +x2 )3/2
E1 = kg2px*0 R rdr/(r2 +x2 )3/2 = =-kg2px(r2 +x2 )-1/2 0 R = =kg2px(1/x–1/(R2 +x2 )) = kg2p(1– x/( R2 +x2 )).
Если xR, то E1 = kg2p получает условие бесконечной заряженной плоскости.
E = 2pg/(4pe0 ) = g/(2e0 ).
9. Поток вектора напряженности:
] $ поле некого вектора А.
ФА = S АdS – поток вектора А через площадку S (скалярная величина).
a - угол между вектором А и нормалью к S.
Он «+» тогда, когда угол a - острый, и «-», когда a - тупой.
Направление нормали n выбирается наружу выпуклой поверхности, а в случае плоской поверхности оговаривается заранее.
ФЕ = S EdS = /E и S вектора/ = =S EndS.
Если поверхность замкнутая, то поток ФЕ обозначается, как
ФЕ = EdS = (q0 /(4pr2 e0 ))dS.
Поток вектора Е через поверхность равен числу силовых линий через эту поверхность. Если поверхность замкнутая, то ФЕ = (q0 /(e0 4pr2 )). dS = =q0 /e0 .
В случае, если заряд окружает неровная поверхность, то ФЕ = q0 /e0 тек же, т.к. число силовых линий, пронизывающих поверхность, останется тем же самым.
Если в поверхности образовать складку, то Ф будет определяться, как поток вектора Е, а в местах складок будет компенсироваться, т.е. ФЕ = q0 /e0 .
10. Теорема Гаусса, уравнение Пуассона.
Рассмотрим систему зарядов:
ФЕ = оЕn dS, где En = E1 + E2 + E3 + + … = SEni , i = 1 N .
ФЕ = oSEni dS = S Eni dS = S(qi /e0 ) = = (Sqi )/e0 , i = 1 N .
Теорема (Остроградского -) Гаусса: Поток вектора Е (ФЕ ) через замкнутую поверхность равен алгебраической сумме зарядов, охватываемых данной поверхностью, поделенной на e0 .
] заряд распределен внутри некого объема с некой объемной плотностью r, тогда q = V rdV. ФЕ = oEdS = /E и S – вектора/ = 1/(e0 e)*V rdV, где V – объем, в котором находятся заряды, а не весь объем области.
e - определяет св-ва среды, в которой находятся заряды (e = 1 в вакууме и/или в воздухе).
Индукция:
Д - прописное.
Д - вектор индукции, отличающийся от Е на некую константу, зависящую от среды.
Д = e0 eE /Д и Е – вектора/;
Ф = оS ДdS = /Д и S – вектора/ = =V rdV – ур-е Максвелла.
11. Бесконечная заряженная плоскость:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Она заряжена с постоянной поверхностной плотностью заряда g.
Она заряжена с постоянной поверхностной плотностью заряда g.
n
E
E E
E E
Выбирается некая поверхность, окруженную зарядом. Определяется вектор Е и ФЕ и точка на основании цилиндрической поверхности. o En dS = (q)/e0 .
Данное направление Е выбирается, т.к. плоскость бесконечна и нет других преимущественных направлений. В любой точке поверхности Е постоянно и a для любой точки одинакова.
o En dS = S б . п . En dS + S осн . En dS = = /aб . п . = 900 / = S осн . En dS = E S осн dS = = E 2S = /по т-ме Гаусса/ = (1/e0 ). g. S.
Е = g/(2e0 ).
12. Поле двух разноименно заряженных плоскостей:
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
Часть векторов Е одинакова по величине, то E = g/e0 .

![]()
![]()
![]()
![]() 13. Поле бесконечного заряженного цилиндра:
13. Поле бесконечного заряженного цилиндра:
![]()
![]()
![]()
|
|
|
|
|
q – заряд на цилиндре.
q = l. t или q = g. 2pR. l
E = t/(2pe0 r)
![]() E
E

![]()
![]() Er
Er
~1/r
![]()
![]() r
r
R
![]()
![]()
![]()
|
|
|
|
|
n
E
ФЕ = E Sб.п. dS = E2prl
q = rVЦ = rpR2 l = 1/e0 rpR2 l
E = (rR2 )/(e0 2r).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
r
![]() l
l
R
q = rpr2 l
Ф = E2prl = (1/e0 ) rpr2 l
E = (rr)/(2e0 )
Если есть e1 и e2 , то e0* e1(2)
E
 1
1
2
![]()
3
r
1 - e1 e2 ;
2 - e1 = e2 ;
3 - e1 e2 .
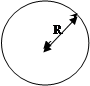
14. Поле бесконечного заряженного шара (сферы):
Заряд с поверхностной плотностью g распределен по сфере радиуса R:
 |
|

Е
|E| - const;
ФЕ = So En dS = E odS = E 4pr2 = = (1/e0 ) g4pR2
q = g 4pR2
Eнаружн = (gR2 )/(e0 r2 ) = q/(4pe0 r2 )

![]()
![]()
![]()
![]()
![]() Eвнутр
= 0
Eвнутр
= 0
E
Er
~1/r
r
R
Заряд с поверхностной плотностью g распределен по шару радиуса R:
Ф = Е 4pr2 = (r/e0 ) 4/3 pR3
qнаружн = rV = r 4/3 pR3
Eнаружн = (gR2 )/(e0 r2 ) = q/(4pe0 r2 )

![]()
![]()
![]()
![]() Eвнутр
= (rr)/(3e0
e1
)
Eвнутр
= (rr)/(3e0
e1
)
E
 |
1
Er
![]()
![]() 2
2
r
R
Шар с r(r):
Eнаружн = q/(4pe0 e2 r2 )
dq = r(r’) 4pr’ dr’
r’ – толщина внутреннего слоя;
q = 0 R r(r’) 4pr’2 dr’
Eнаружн = (4p 0 R r(r’) 4pr’2 dr’)/ /(4pe0 e2 r2 ); r
Eвнутр = (4p 0 r(r’) 4pr’2 dr’)/ /(4pe0 e1 r2 );
Шар с полостью:
Eнаружн = (4p R1 R2 r(r’) 4pr’2 dr’)/ /(4pe0 e2 r2 ); r
Eвнутр = (4p R1 r(r’) 4pr’2 dr’)/ /(4pe0 e1 r2 ).
15. Потенциал ( j):
]$ поле, создаваемое неподвижным точечным зарядом q. ]$ точечный заряд q’, на который действует сила:
F = 1/(4pe0 )* (qq’)/r2
Работа, совершаемая над зарядом q’ при перемещении его из одной точки в другую, не зависит от пути
A12 = 1 2 F(r)dr = (qq’)/(4pe0 )r1 r2 dr/r2 .
Иначе ее можно представить, как убыль потенциальной энергии:
A12 = Wp1 – Wp2 .
При сопоставлении формул получаем, что Wp = 1/(4pe0 )* (qq’)/r.
Для исследования поля воспользуемся двумя пробными зарядами qПР ’ и qПР ’’. Очевидно, что в одной и той же точке заряды будут обладать разной энергией Wp ’ и Wp ’’, но соотношение Wp /qПР будет одинаковым.
j = Wp /qПР = 1/(4pe0 )* q/r называется потенциалом поля в данной точке и, как напряженность, используется для описания электрического поля.
]$ поле, создаваемое системой из N точечных зарядов. Работа, совершаемая силами этого поля над зарядом q’, будет равна алгебраической сумме работ, совершаемых каждым из qN над q’ в отдельности:
A = i = 1 N Ai, где Ai = = 1/(4pe0 )* (qi q’/ri 1 - qi q’/ri 2 ), где ri 1 - расстояние от заряда qi до начального положения заряда q’, а ri 2 – расстояние от qi до конечного положения заряда q’.
Следовательно Wp заряда q’ в поле системы зарядов равна:
Wp = 1/(4pe0 )*i = 1 N (qi q’)/ri , то
j = 1/(4pe0 )* i = 1 N (qi/ri ), следовательно потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Заряд q, находящийся в точке с потенциалом j обладает энергией
Wp = qj, то работа сил поля
A12 = Wp1 –Wp2 = q(j1 - j2 ).
Если заряд из точки с потенциалом j удалять в бесконечность, то A = qj, то j численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность.
16. Связь между напряженностью и потенциалом:
Электрическое поле можно описать с помощью векторной величины Е и скалярной величины j.
Для заряженной величины, находящейся в электрическом поле:
F = qE, Wp = qj.
Можно написать, что
E = - ¶j/¶x - ¶j/¶y - ¶j/¶z, т.е. при проекции на оси:
Ex = -¶j/¶x, Ey = -¶j/¶y, EZ = -¶j/¶z, аналогично проекция вектора Е на произвольное направление l: Еl = = -¶j/¶l, т.е. скорости убывания потенциала при перемещении вдоль направления l.
j = 1/(4pe0 )* q/r = /в трехмерном пространстве/ = 1/(4pe0 )* q/(x2 +y2 +z2 ).
Частные производные этих функций равны:
¶j/¶x = -q/(4pe0 )* x/r3 ;
¶j/¶y = -q/(4pe0 )* y/r3 ;
¶j/¶z = -q/(4pe0 )* z/r3 .
При подстановке получаем:
E = 1/(4pe0 )* q/r2 .
Работа, по перемещению q из точки 1 в точку 2, может быть вычислена, как A12 = 1 2 qEdl или A12 = q(j1 - j2), приравняв их, получим j1 - j2 = 1 2 Edl. При обходе по замкнутому контуру j1 = j2, то получим: o Edl = 0.
17. Эквипотенциальные поверхности:
Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной. Ее уравнение имеет вид j(x, y, z) = const.
При перемещении по эквипотенциальной поверхности на отрезок dl, dj = 0. Следовательно, касательная к поверхности, составляющая вектор Е, равна 0, т.е. вектор Е направлен по нормали к эквипотенциальной поверхности. Т.е. линии напряженности в каждой точке перпендикулярны к эквипотенциальным поверхностям.
Эквипотенциальную поверхность можно провести через любую точку поля и их можно построить бесконечное множество. Их проводят таким образом, чтобы разность потенциалов для двух соседних поверхностей была одинаковой (Dj = const). Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряженности поля.
В соответствии с характером зависимости Е от r, эквипотенциальные поверхности при приближении к заряду становятся гуще. Для однородного поля эквипотенциальные поверхности представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению поля.
18. Проводники в электрическом поле:
Проводники состоят из связанных зарядов равномерно распределенных по объему проводника. Электроны проводника находятся в тепловом хаотическом движении.

![]()
![]()
![]()
![]()
![]() ]$ поле с проводником:
]$ поле с проводником:
() 1
- + Е
![]() - +
- +
- + Е
![]() - +() 2
- +() 2
- + Е
![]() - +
- +
-- + Е
![]() -
+
-
+
+ Е
- +
Напряженность внутри проводника равна 0, т.к. внутри проводника складывается некая суперпозиция напряженностей.
Если j1 - j2 = 0, то поверхность проводника эквипотенциальна, а линии напряженности всегда перпендикулярны эквипотенциальной поверхности.
Возьмем произвольную точку плоскости проводника.
t
j
Возьмем касательную к элементу поверхности t.
dj/dt = -Et, (где dj/dt = 0) вектор Е перпендикулярен плоскости в данной точке.
![]()
 q
q
Е = 0
E ~ g
(g - поверхностная плотность)
Заряд распределен по поверхности, Е = 0, распределение неравномерно, максимальную плотность заряд имеет в местах максимальной кривизны.
Обозначим «степень кривизны» за С, то С = 1/R.
E ~ g ~ C ~ 1/R.
19. Электроемкость, конденсаторы:
Электроемкость – коэффициент пропорциональности между зарядом проводника и потенциалом, который заряд приобретает. Зависит от формы проводника и окружающих его тел.
С = q/j.
Электроемкости уединенных проводников (на него ни что не влияет):
![]() Сфера: q
Сфера: q
 j = 1/(4pe0
)*
q/R
j = 1/(4pe0
)*
q/R
C = q/j = 4pe0 R
![]() R j
R j
Если поместить около сферы другой проводник, то С = Dq/Dj.
-Dq
 |


![]() R
R
Dq
 E+
E+
![]()
 X E-
X E-
+Dq
l
![]() R
R
Dj - разность потенциалов, возникшая между проводниками.
Если lR, то заряд по поверхности каждой сферы распределяется равномерно.
Dj = j1 - j2
j1 - j2 = R l-R Edx
E = E+ + E- = k* Dq/x2 + k* Dq/(l-x)2
Конденсаторы:
С = 4pe0 R
Плоский:
q+ q- C = Dq/(j1 - j2) =
= (Dqe0 S)/(Dqd) =
= e0 S/d
j1 - j2 = E* d =
= gd/e = (Dqd)/(e0 S)
![]()
![]()
![]() j1 j2
j1 j2
Сферический:
R1
R2
+q
-q
j1 - j2 = R1 R2 E+ dr = = Dq/(4pe0 ) * R1 R2 (1/r2 )dr = = Dq/(4pe0 )* (1/R1 – 1/R2 ).
C = (4pe0 eR1 R2 )/(R2 -R1 ).
20. Электрическое поле в диэлектриках:
При помещении в поле диэлектрика в поле происходит изменение. Сам диэлектрик реагирует на поле иначе, чем проводник.
Заряды, входящие в состав молекул диэлектрика, называются связанными. Они не могут покидать пределы молекулы, в которую они входят.
Заряды не входящие как в состав молекул диэлектрика, так и в сам диэлектрик называются сторонними.
Поле в диэлектрике является суперпозицией полей сторонних и связанных зарядов и называется микроскопическим (или истинным).
ЕМИКРО = ЕСТОР + ЕСВЯЗ
Микроскопическое поле в пределах диэлектрика непостоянно, поэтому
Е0 = ЕМИКРО = ЕСТОР + ЕСВЯЗ
ЕСВЯЗ = E’
Макроскопическое поле:
E = E0 + E’
При отсутствии диэлектрика макроскопическое поле равно
Е = Е0 = ЕСТОР .
Если сторонние заряды неподвижны, то поле ЕМИКРО обладает теми же свойствами, как электростатическое поле в вакууме.
![]() При определении суммарного действия всех электронов имеет значение и центр масс отрицательных зарядов.
При определении суммарного действия всех электронов имеет значение и центр масс отрицательных зарядов.
®
q- l q+
 |
® ®
r- r+
® ®
r- = (i = 1 N ri qi -)/( i = 1 N qi -)
®
r+ = (j = 1 N rj qj +)/( j = 1 N qj +)
Полярные и неполярные молекулы во внешнем поле приводят развороту диполя в направлении поля. Неполярные молекулы приобретают электрический момент. Они поляризуются, от чего возникает дипольный момент, направленный вдоль внешнего поля. Молекула ведет себя как упругий диполь.
21. Диполь в однородном и неоднородном электрических полях:
В однородном поле:
|
![]() E
E
l +q
![]()
![]()
![]()
![]()
![]()
![]() Fk
Fk
![]() ®
®
![]() M a
M a
![]() Fk
(X)
-q
Fk
(X)
-q
M = Fk* l* sina = q* E* l* sina = = P* E* sina, где P – дипольный момент.
® ® ®
M = [P x E]
®
M – направлен «от нас»
dA = Mda = P* E* sina da
dA = dW ® ®
W = -P E cosa = -(P E)*
* - cкалярное произведение.
В неоднородном поле:
® ®
|
![]()
![]()
![]() l
l
![]()
![]()
![]()
![]()
![]()
![]() -q D
X
-q D
X
![]()
![]() ®
®
F-
DF = (F+) – (F-) = q* DE = = q* ¶E/¶X* l* cosa = P* ¶E/¶X* cosa = = /кроме вращающего момента на диполь действует сила, зависящая от угла a, если угол острый, то диполь «втягивается» внутрь поля/ = = ¶(PEcosa)/¶X = -¶W/¶X.
22. Поляризация диэлектриков:
®
Р – параметр, описывающий состояние диэлектрика в электрическом поле.
® ®
P = (i = 1 N Pi)/DV
 |
(-+)(-+) (-+)(-+)
(-+)(-+) (-+)(-+)
(-+)(-+) (-+)(-+)![]()
(-+)(-+) (-+)(-+)
(-+)(-+) (-+)(-+) ®
![]() (-+)(-+) (-+)(-+) Е
(-+)(-+) (-+)(-+) Е
(-+)(-+) (-+)(-+)
(-+)(-+) (-+)(-+)
![]() (-+)(-+) (-+)(-+)
(-+)(-+) (-+)(-+)![]()
На поверхности возникают связанные заряды с плотностью gСВЯЗ .
® ®
P = He0 E
H – коэффициент диэлектрической восприимчивости;
Е – результирующий вектор.
 |
![]()
![]()
![]() E
E
![]()
 DS l
DS l
![]()
![]()
![]() ® n
® n
![]() P
P
![]() n
n
d
-g +g
P* DV – суммарный дипольный момент молекул внутри цилиндра.
DV = DS* l* cosa
P* DV = P* DS* l* cosa = q* l
q = gСВЯЗ * DS
P* DS* cosa* l = gСВЯЗ * DS* l
P* cosa = gСВЯЗ
gСВЯЗ = He0 E, где Е – результирующее поле в диэлектрике.
® ® ®
Е = Е0 + Е’
Внешнее поле должно ослабляться:
® ® ® ® ®
Д = e0 Е + Р = e0 E + He0 E =
® ®
= (1 + H)e0 E = ee0 E.
23. Поле внутри плоской диэлектрической пластины:
![]()
![]()
![]()
![]()
![]() +g0
-g0
+g0
-g0
Е0
![]() - +
- +
![]() - +
- +
![]()
![]() - +
- +
![]()
g0 – свободные перемещающиеся заряды, создающие Е0 (вектор);
Число силовых линий уменьшается во столько раз, какое значение имеет e.
Е0 = g0 /e0
Е = Е0 – Е’ = g0 /e0 - gСВЯЗ /e0 = = 1/e0 (g0 - gСВЯЗ );
E = E0 – HE ® E* (1 +H) = E0 ® E = E0 /(1+H) = E0 /e;
Д = e0 eE = e0 E, т.е. вектор индукции внутри не изменяется, плотность силовых линий остается постоянной.
E = 1/e0* (g0 - gСВЯЗ ) = E0 /e =g0 /(e0 e);
gCВЯЗ = g0* (e - 1)/e.
25. Сегнетоэлектрики:
Существуют группы веществ, которые могут обладать самопроизвольной поляризованностью в отсутствие внешнего поля. Подобные вещества получили название сегнетоэлектриков.
Впервые свойства сегнетоэлектриков было изучено Курчатовым.
Отличия сегнетоэлектриков от остальных диэлектриков:
1) Диэлектрическая проницаемость сегнетоэлектриков измеряется тысячами, а у диэлектриков – десятками.
2) Диэлектрическая проницаемость сегнетоэлектриков зависит от напряженности поля.
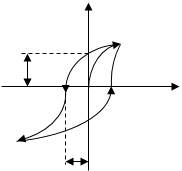
3) Сегнетоэлектрики обладают явлением гистерезиса (запаздывания):
 P
P
1
Pr 2 3
E
EC
При изменении поля значение поляризованности Р и смещения D отстают от напряженности поля Е, в результате чего P и D зависят не только от текущего значения Е, но и от проедшествующего. Это явление называется гистерезисом.
На участке (2), при обращении Е в ноль, сохраняется остаточная поляризованность Pr. Она становится равной нулю только под действием противоположнонаправленного поля ЕС , называемой коэрцетивной силой.
Сегнетоэлектриками могут быть только кристаллические вещества с отсутствующим центром симметрии.
У каждого сегнетоэлектрика $ темпиратура, называемая точкой Кюри, при которой он утрачивает свои свойства и становиться обычным диэлектриком.
26. Поведение векторов напряженности и индукции на границе двух сред:
Et1
![]()
![]()
![]() e1
e1
![]() ®
®
® n1
![]() En1
a1
En1
a1
![]()
![]()
![]()
![]()
![]() dh
dh
![]()
![]()
![]() Et2
Et2
a2 ® ®
![]() En2
n2
En2
n2
e2
Выделим на границе сред тонкую «шайюбу» толщиной dh ® 0 и площадью S. Подсчитаем поток индукции Д через выделенный объем.
Дn2* S* cos0o + Дn1* S* cos180o + ФБОК = 0, где Ф = 0, т.к. dh ® 0;
Дn2* S - Дn1* S = 0 ® Дn2 = Дn1 ® ® e0 e2 En2 = e0 e1 En1 ® En2 /En1 = e1 /e2 .
Дn – неприрывна, а Еn терпит разрыв. ®
Рассмотрим циркуляцию вектора Е по контуру на границе раздела с dh ® 0:
®
![]()
![]() ® E1
t
® E1
t
![]() E1
E1
![]()
![]()
![]()
![]()
![]() Et2
Et2
![]() l
l
![]() Et1
Et1
E2
![]() ®
®
E2 t
E1 t l cos0o + E2 t l cos180o + + EБОК dh cos90o = 0;
Et1 = Et2 ; Дt1 /(e0 e1 ) = Дt2 /(e0 e2 ) ® ® Дt1 / Дt2 = e1 /e2 (Е1 и Д1 сонаправленны, как и Е2 и Д2 );
tga1 /tga2 = (Et1 / En1 )* (En2 /Et2 ) = = En2 /En1 = e1 /e2 .
27. Энергия электрического плоля:
Плотность энергии – энергия, приходящаяся на единицу объема поля.
w = W/V – в однородном поле;
w = dW/dV - в неоднородном поле.
[w] = Дж/м3 ;
Определим w в поле плоского конденсатора:
W = CU2 /2 = (e0 eSU2 )/(2d), где U – разность потенциалов на обкладках конденсатора;
d – расстояние между обкладками;
V = S* d;
w = W/V =(e0 eSU2 )/(2d* Sd) = = (e0 eU2 )/(2d2 );
U/d = E;
w = (e0 eE2 )/2 = EД/2 = Д2 /(2e0 e)
В сегнетоэлектриках w = 1/2 S петли гистерезиса.
Очевидно, что w характеризует поле в конкретной точке, как Е и Д.
W = V wdV – энергия поля.
Энергия взаимодействия двух точечных зарядов:
W = q1* j2 = (q1 q2 )/(4pe0 er) – энергия взаимодействия, она делится поровну между зарядами.
Энергия одного заряда:
Wi = 1/2 qi ji ;
Энергия поля из N зарядов:
W = 1/2 i=1 N qi ji , при этом i 2.
28. Классическая теория электропроводности металлов:
Существует предположение, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движуться совершенно свободно, пробегая в среднем некоторый путь l. Но в отличии от газа, электроны в металле сталкиваются приемущественно не сами с собой, а с ионами, образующими кристаллическую решетку металла.
Оценку средней скорости теплового движения электронов можно произвести по формуле:
u = (8kT)/(pm), для комнатной темпиратуры u » 105 м/с.
При включении поля на хаотическое тепловое движение, происходящее с u, накладывается упорядоченное движение электронов с u:
j = neu, где j – плотность тока; для меди u » 10-3 м/с.
Вызываемое полем изменение среднего значения кинетической энергии электронов.
(u + u)2 = u2 + 2uu + u2 = = u2 + 2uu + u2
(u + u)2 = u2 + u2 , значит упорядоченное движение увеличивает кинетическую энергию в среднем на Dek = (mu2 )/2.
29. Природа носителей зарядов металла:
В результате проведения ряда опытов /трамвайная линия/ было доказано, что заря в металлах переносится не атомами, а другими частицами, предположительно электронами. Если это так, то при резком торможении частицы должны продолжить свое движение и перенести некоторый заряд.
] проводник движется со скоростью v0 и резко затормаживается с ускорением w. Продолжая двигаться по инерции, носители приобретут ускорение –w. Такое же ускорение можно создать, подействовав на проводник электрическим полем с E = -mw/e’, т.е. приложив к концам проводника разность потенциалов:
j1 - j2 = 1 2 Edl = -1 2 (mw)/e’dl = = -mwl/e’, где l – длина проводника. В этом случае по проводнику потечет ток I = (j1 - j2)/R.
Таким образом за время торможения прошел заряд
q = dq = -u0 0 ml/(e’R)du = = (m/e’)* (lu0 /R), заряд положителен, если он переносится в направлении движения проводника.
Существование в металлах свободных электронов можно объяснить тем, что при образовании кристаллической решетки, от атомов отщепляются слабее всего связанные электроны.
30. Закон Видемана – Франца:
Известно, что металлы обладают как высокой электропроводностью, так и большой теплопроводностью. Видеман и Франц в 1853 году установили, что отношение коэффициента теплопроводности Н к коэффициенту электропроводности s для всех металлов примерно одинаковое и изменяется пропорционально абсолютной темпиратуре. Тот факт, что теплопроводность металлов значительно превышает теплопроводность диэлектриков говорит о том, что и теплопроводность в металлах осуществляется с помощью свободных электронов.
Рассматривая электроны как одноатомный газ получим:
H = 1/3 nmulCV , где СV = 3/2 (k/m), то H = 1/2 nkul.
Таким образом
H/s = (kmu2 )/e2 = 3(k/e)2 T = = 2,23* 10 8 * T.
31. Постоянный электрический ток, его плотность и ЭДС:
Если через некоторую поверхность переносится суммарный заряд, отличный от нуля, то говорят, что через эту поверхность течет электрический ток. Ток может течь в тветдых телах (металлы, полупроводники), в жидкостях (электролиты) и газах (называется газовым разрядом).
Для протекания тока необходимо наличие заряженных частиц, которые могут перемещаться в пределах всего тела, называемых носителями тока. Ими могут быть электроны, ионы или макроскопические частицы, несущие на себе избыточный заряд.
Ток возникает при условии, что внутри тела $ эл. поле. Носители заряда принимают участие в молекулярном тепловом движении и движуться с некой v и в отсутствии заряда, но т.к. движение хаотическое, то ток = 0. При появлении поля на хаотическое v накладывается упорядоченное u. Т.о. u = v + u, но т.к. v = 0, то u = u.
Значит эл. ток – упорядоченное движение электрических зарядов.
Эл. ток колличественно характеризует величина, равная величине заряда, переносимого через рассматриваемую поверхность за единицу времени, и называемая силой тока, т.е. поток заряда через поверхность.
I = dq/dt, где dt – время, за которое через поверхность переносится заряд dq.
Перенос “-“ заряда в одном направлении эквивалентен переносу такого же “+” заряда в противоположном направлении. Если через поверхность одновременно переносится «+» и «» заряды, то
I = dq+ /dt + |dq |/dt.
За направление тока принимается направление движения «+» носителей.
Эл. ток может быть распределен по поверхности, по которой он течет неравномерно. Это показывает вектор плотности тока j. Он численно равен отношению {силы тока dI, протекающего через расположенную в данной точке перпендикулярную к направлению движения носителей площадку dS^ } и {величины этой площадки}:
j = dI/dS^ , за его направление принимается u.
Ток, не изменяющийся по времени, называется постоянным:
I = q/t, где q – заряд, переносимый через рассматриваемую поверхность за конечное время t.
I = [A].
ЭДС:
Если в проводнике создать электрическое поле и не принимать мер к его поддержанию, то очень быстро ток прекратится. Для недопущения этого необходимо осуществлять круговорот зарядов по самкнутому пути. В замкнутой цепи должны иметься участки, на которых перенос положительных зарядов происходит в направлении возрастания j, т.е. против сил эл. поля. Перемещение носителей на этих участках возможно только под действием сторонних сил.
Их можно охарактеризовать работой, которую они совершают над перемещающимися по цепи зарядами. Величина, равная работе сторонних сил над единичным «+» зарядом, называется ЭДС.
e = A/q.
FСТ = E** q, где Е* - напряженность поля сторонних сил.
Величина, равная работе, совершаемой электростатическими и сторонними силами при перемещении единичного «+» заряда, называется падением напряжения (напряжением):
U12 = j1 - j2 + e12 .
Участок цепи, на котором не действуют сторонние силы, называется однородным, тогда:
U = j1 - j2.
Участок, на котором на носитель действуют сторонние силы, называется неотнородным.
32. Закон Ома, сопротивление проводников, закон Джоуля – Ленца:
Закон Ома: сила тока, текущего по однородному металлическому проводнику, при отсутствии сторонних сил, пропорциональна падению напряжения U на проводнике.
I = (1/ R)* U , т.к. проводник однородный, то U = j1 - j2; R – электрическое сопротивление проводника.
[A] = [Ом]/[B].
Величина сопротивления зависит от формы, размеров и свойств материала проводника. Для однородного цилиндрического проводника:
R = r(l/S), где l – длина проводника, S – площадь поперечного сечения, r - удельное электрическое сопротивление, зависящее от свойств металла.
r = [Ом* м].
В металлах направление векторов Е и j (плотность тока) совпадают. Из этого следует, что
j = (1/r)* E = sE (закон Ома в дифференциальной форме), где s - удельная электрическая проводимость материала.
Закон Джоуля – Ленца:
Когда проводник неподвижен и химических превращений в нем не совершается, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается, выделяется тепло:
Q = Uit = /по закону Ома/ = RI2 t, закон получил название Джоуля – Ленца.
Если сила тока изменяется со временем, то кол-во теплоты за время t: Q = 0 t RI2 dt.
Кол-во тепла в элементарном цилиндрическом объеме:
dQ = RI2 dt = ((rdl)/dS)(jdS)2 dt = = rj2 dVdt, где dV = dS* dl.
Поделив выражение на dV и dt, получим кол-во теплоты, выделевшееся в ед. V за ед. t:
QУД = rj2 – удельная тепловая мощность тока.
33. Закон Ома для для неонородного участка цепи:
На неоднородном участке цепи на носители тока действуют, кроме электрических сил еЕ, сторонние силы еЕ*, способные так же вызывать упорядоченное движение носителей тока. На таких участках:
j = s(E + E*) – закон Ома для неоднородного участка цепи в дифференциальной форме.
Для того, чтобы перейти от дифференциальной формы к интегральной:
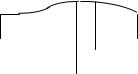
Неоднородный участок цепи 1 – 2:
![]() S
S
 |
![]()
![]()
![]()
![]() 1 2
1 2
dL
Предположим, что значения j, s, E, E* в каждом сечении, ^ контуру 1–2, одинаковы; векторы j, E и Е* в каждой точке направлены по касательной к контуру.
Спроецировав на элемент контура dl векторы j, E и Е*, получим:
(*) jL = s(EL + EL *), где проекции равуны модулю векторов, взятых со знаком «+» или «», в зависимости от направления вектора относительно dL.
Из-за сохранения заряда сила постоянного тока в каждом сечении будет одинаковой, то I = jL S постоянна вдоль контура 1 – 2.
В (*) можно заменить: j = I/S, s = 1/r, то:
I(r/S) = EL + EL *, а по всей длине:
I1 2 (r/S)dL = 1 2 EL dL + 1 2 EL *dL
IR = j1 - j2 + e12 I = (j1 - j2 + e12 )/R – закон Ома для неоднородного участка цепи.
Если цепь замкнута, т.е. j1 = j2, то: I = e/R, где R – cуммарное сопротивление всей цепи.
34. Разветвление цепи. Правила Кирхгофа:
Узлом называется точка, в которой сходятся более, чем 2 проводника. Токи, текущие к и от одного узла, разноименны.
Первое правило: алгебраическая сумма токов, сходящихся в узле, равна 0:
IK = 0, что вытекает из закона сохранения заряда (суммарный заряд электрически изолированной системы не может изменяться), то поток вектора j должен быть равен 0.
![]() Второе правило:
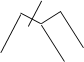
рассмотрим контур:
Второе правило:
рассмотрим контур:
![]() () 2
() 2
![]() R1 R2
R1 R2
 |
e![]()
![]()
![]()
![]() 1 + + e2
1 + + e2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() () R3 ()
() R3 ()
![]() 1 + 3
1 + 3
Применим закон Ома:
![]() I1
R1
= j1 - j2 + e1
,
I1
R1
= j1 - j2 + e1
,
I2 R2 = j2 - j3 + e2 , +
I3 R3 = j3 - j4 + e3 ,
I4 R4 = j 4 - j 1 + e 4 .
IK RK = eK – II пр-ло.
I1 I2
![]()
![]()
I3
![]()
![]()
![]()
R1 R2 R3
![]()
![]() + +
+ +
![]()
![]()
![]()
![]() - -
- -
![]()
![]()
![]()
![]()
![]()
![]() j1 0 j2
j1 0 j2
e1 e2
![]()
![]() C
C
I1 R1 + I3 R3 = -e1
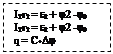 I1
R1
+ I2
R2
= -e1
+e2
I1
R1
+ I2
R2
= -e1
+e2
35. Магнитное поле в вакууме:
Взаимодействие токов осуществляется через поле, называемое магнитным. Из опытов следует, что оно имеет направленный характер и должно характеризоваться векторной величиной, называемой магнитной индукцией (В), аналогичной величине Е в магнитном поле. Вспомогательную величину называют напряженностью магнитного поля (Н), аналогичной D электрического поля.
Магнитное поле, в отличие от электрического, не оказывает воздействия на покоящийся заряд. Сила возникает только когда заряд начинает двигаться.
Проводник с током представляет собой электрически нейтральную систему зарядов, значит магнитное поле пораждается толко движущимися зарядами.
Движущиеся заряды изменяют св-ва окружающего пространства, создавая в нем магнитное поле, проявляющегося в воздействии сил на движущиеся заряды.
Для магнитного поля так же справедлив и принцип суперпозиции:
Поле В, пораждаемое несколькими движущимися зарядами, равно векторной сумме полей Bi , пораждаемых каждым зарядом в отдельности; В = Bi .
Для двух бесконечных проводников сила их взаимодействия для единицы длины каждого из проводников равна:
f = k(2I1 I2 )/l, где l – расстояние между проводниками.
1А – такая сила неизменяющегося тока, проходящего по двум проводникам, находящимся в вакууме на рассоянии в 1м, которая вызывает между проводниками силу, равную 2* 107 Н/м.
1Кл – заряд, проходящий через сечение проводника за 1с и силе тока 1А.
f = [m0 /(4p)]* (2I1 I2 )/l
2* 107 = [m0 /(4p)]* 2(1* 1)/1 ® ® m0 = 4p* 107 (Гн/м).
Взаимодействие между токами осуществляется по средствам магнитного поля.
В качестве пробного элемента выбирается замкнутый контур.
® ®
I n
![]()
Ориентация контура может быть задана направлением нормали, определяемой методом «винта». За направление магнитного поля (В) так же принимается направление нормали.
a = 90о ® m - мах;
a = 0 ® m = 0;
mМАХ ~ I
mМАХ ~ I* S
mМАХ ~ S ® ®
Устан.момент магн. диполя: PM =I* S* n
mMAX /PM ~ B.
36. Закон Био – Савара:
Величина напряженности должна зависеть от силы тока в проводнике, от расстояния от наблюдаемой точки до проводника и от угла наклона.
I

![]()
![]() dB
dB

r
![]()
![]() a
a
dl
®
Можно определить Н в некой точке:
® ®
dH = k(I[dl x dr])/r3 – закон Био – Савара – Лапласса, позволяющий вычислить напряженность для любых условий.
[H] = А/м; [B] = Тл.
![]() I
I
![]() (X)
(X)
![]()
a
da
®
r
![]() dr
dr
dL

dH = k(I* dL* sina)/r2
dL = dr/sina = rdr/sina = bda/sin2 a
r2 = b2 /sin2 a
dH = I/(4p)* (bda)/sin2 a* (sin2 a/b2 )* sina = = I/(4p)* (sina da)/b;
p
H = I/(4pb) 0 sina da = I/(2pb);
![]() H = I/(2pb) – частный случай.
H = I/(2pb) – частный случай.
 |
I
a1
![]()
![]() a2
a2
H = [I/(4pb)]* (cosa1-cosa2)
37. Поле прямого и кругового тока:
![]() I
I
![]() (X)
(X)
![]()
a
da
®
r
![]() dr
dr
dL

dH = k(I* dL* sina)/r2
dL = dr/sina = rdr/sina = bda/sin2 a
r2 = b2 /sin2 a
dH = I/(4p)* (bda)/sin2 a* (sin2 a/b2 )* sina = = I/(4p)* (sina da)/b;
p
H = I/(4pb) 0 sina da = I/(2pb);
![]() H = I/(2pb) – частный случай.
H = I/(2pb) – частный случай.
 |
I
a1
![]()
![]() a2
a2
H = [I/(4pb)]* (cosa1-cosa2)
Линии магнитной индукции магнитного поля прямого тока представляют собой систему охватывающих провод концентрических окружностей.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ®
®
I
Поле кругового тока:
®
![]()
![]()
![]()
![]()
![]()
![]() ® dH
® dH
![]()
![]()
![]() dl R
r
dl R
r
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
X
dH = 1/(4p)* (Idl)/R2
2pR
H = I/(4pR)*0 dl = I/(2R)
dH = dH sina = dH(R/r)
dH = 1/(4p)* (Idl)/r2 * R/r
H = 1/(4p)* (2pR2 I)/r3 = = 1/(4p)* (2pm)/r 3 , x R ®
® H = 1/(4p)* (2pm)/x3
![]() H
= 1/2*
(2pR3
I)/(R2
+ x2
)3/2
, если (x R).
H
= 1/2*
(2pR3
I)/(R2
+ x2
)3/2
, если (x R).
![]()
![]()
![]() ®
®
![]() H1
H1
![]()
![]()
![]()
![]()
![]()
![]() ®
®
![]()
![]()
![]() H
H
®
![]()
![]() H
H2
H
H2
® ®
I I
1 2
Напряженность магнитного поля, создаваемая круговыми токами на точке плоскости, относительно которой витки симметричны, будет ориентирована оси витков.
38. Поле соленоида:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Соленоид – цилиндрический каркас бесконечной длины с намотанным на него проводом.
Соленоид – цилиндрический каркас бесконечной длины с намотанным на него проводом.
®
![]()
![]()
![]()
![]()
![]()
![]() I
I
1 2
![]() 1’
2’
1’
2’
® ® 4 3
oH dl = 1 2 Hdl + 2 3 Hdl + 3 4 Hdl + + 4 1 Hdl;
H1 2 dl = H* l = Inl;
H = I* n , где n – плотность обмотки.
Поле внутри соленоида однородно.
Поле снаружи соленоида равно 0.
H1’ 2’ = 0.
39. Сила Лоренца. Закон Ампера:
На заряд, движущийся в магнитном поле, действует сила, называемая магнитной и определяемая зарядом q, скоростью движения v и магнитной индукцией В. Направление вектора F определяется направлением v и В.
® ® ®
F = q* [v x B];
Это выражение было получено Лоренцем путем обобщения экспериментальных данных и получило название силы Лоренца.
®
![]() F¶
F¶
![]() ® ®
® ®
B1 q1 v1
![]()
![]() (*
) ( )
(*
) ( )
®
B2 ®
![]()
![]()
![]() (x)
( ) v2
(x)
( ) v2
q2
®
F¶
® ® ®
FЛ = q* [v x B];
® ® ® ®
FЛ = q* [v x B] + q* E
F = 1/(4pe)* (q1 q2 )/r2
FЛ = qvB = qv* (m0 /4p)* (v/r2 )* q2 (?)
B2 = m0 /(4p)* (I2 dl)/r2 = = m0 /(4p)* (q2 /dt)* (dl/r2 ) = m0 /(4p)* (q2 v)/r2
FЛ /F¶ = m0 e0 v2 = v2 /C2 .
Закон Ампера:
® ® ® ®
F = e [(u + u), B];
u - тепловая скорость;
u – скорость направленного движения;
® ® ®
F = e [u, B];
dV = S* dl;
® ® ® ®
F = F* nS* dl = en [u, B] S* dl;
® ®
en u = j;
® ® ®
F = [j, B] dV;
® ® ® ®
FЕД. ОБ. = F/dV = [j x B];
® ®
j* S* dl = I* dl;
® ® ®
dF = I [dl x B] – сила Ампера.
40. Контур с током в магнитном поле, вращательный момент:
a

b ® ® ®
FA FA B
(x) (*)
I
FA = IaB
![]() M = IabB = ISB = PM
B, где РМ
– магнитный момент. (?) ®
M = IabB = ISB = PM
B, где РМ
– магнитный момент. (?) ®
FA
b ®

![]() FA
FA
a
® ®
(X) n (X) B
![]() ®
®
![]()
![]() FA
FA
®
FA
® ® ®
F = I [l x B];
® ® ®
M = [PM B];
![]()
 Контур произвольной формы:
Контур произвольной формы:
dh
![]()
![]() dl1
dl2
®
dl1
dl2
®
B
®
I
![]()
![]()
![]()
![]()
![]() I a
I a
® a1 ®
![]()
![]()
![]() dl1
(X)
FЛ
dl2
(*
)
FЛ
®
dl1
(X)
FЛ
dl2
(*
)
FЛ
®
![]()
![]() ® a2
B
® a2
B
I
dF1 = I dl1 B sina1 = IB dh
dF2 = I dl2 B sina2 = IB dh
dM = dF* a = Iba dh = IB dS
M = ISB = PM B
® ® ®
M = [PM B]
dA = M da = PM B sina da
dA = dWp
A = Wp = 0 a M da = -PM B cosa + const – потенциальная энергия контура с током в магнитном поле.
a = p/2 ® Wp = const = 0
Wp = -PM B cosa = -(PM B)
41. Работа по перемещению контура с током в магнитном поле:
![]()
![]() ®
®
![]()
![]()
![]()
![]()
![]()
![]() I
I
![]() ®
®
![]() + I
+ I
![]()
![]()
![]()
![]() l
l
® FA
![]() (X) B
(X) B
![]() ®
®
I dx
dA = FA dx = IB (l dx) = IB dS = I dФ;
dФ – поток магнитной индукции, пересекаемый проводником.
Если В (вектор) не ^ контуру, то
dA = Ibl cosa dx = IBn dS = I dФ, т.к.
dФ = B dS = B cosa dS = Bn dS
На совершение работы идет ресурс источника тока, его ЭДС.
![]()
![]()
![]()
![]()
![]()
![]() Индукционный поток направлен противоположно току I.
Индукционный поток направлен противоположно току I.
1 2
® ®
I I
ФН ® Ф0 ФК
(X) B
2 2
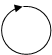
A1 = I (ФН – Ф0 )
А2 = I (Ф0 – ФK ) (?)
A = A1 + A2 = I (ФК – ФН ) = I DФ.
®
 I
I
®
(X) B
A = -IBS – IBS = -2IBS.
42. Магнитное поле в веществе:
Первоначально поле в вещ-ве рассматривалось как поле от микротоков.
Движение зарядов обуславливает магнитный момент и они рассматриваются как некая система.
® ® ®
B = B0 + B’.
Введем вектор, характеризующий магнитные св-ва и связанный с (i=1 N PMi )/DV:
®
J = (i=1 N PMi )/DV
[ J ] = A/м;
J = c H, где c - магнитная восприимчивость.
cУД = c/r = [м 3 /кг], где r - плотность вещ – ва.
cМОЛ = c* nКмоль [м3 /Кмоль].
44. Описание магнитного поля в магнетике:
Существует 3 класса магнетиков:
1) Диамагнетики (cМОЛ 0, 107 108 (м3 /Кмоль));
2) Парамагнетики (cМОЛ 0, 106 107 (м3 /Кмоль));
3) Ферромагнетики (cМОЛ 0, 103 104 (м3 /Кмоль)).
Электрическое поле в веществе может только ослабляться. В магнитном поле оно либо усиливается, либо ослабляется.
® ® ® ® ®
H = B/m0 – J = B/m0 - cH
® ®
H(1 + c) = B/m0
® ®
H = B/(m0 m); m = 1 + c.
Внесем в магнитное моле магнетик:
®
![]() B0
B0
![]()
![]()
![]()
![]()
![]()
![]() (X)(X)
(X)(X)
![]() (X)(X)
(X)(X)

![]()
![]() (X)(X) B’
(X)(X) B’
![]()
dl микротоки
® ® ®
B = B0 + B’
B’ = m0* Il
dPM = Il* S* dl
dPM /dV = J = Il
® ® ®
B = B0 + m0 J
® ® ® ® ®
H = B/m0 – J = B0 /m0 = H0 (теоретически)
® ® ®
H = H0 – H0 , где Н0 – размагничивающее поле;
® ®
H0 = N* J (фактор размагничивания)
N = 1 для тонкого диска;
N = 1/3 для шарика.
Если однородный магнетик помещается во внешнее однородное поле, то внутреннее поле магнетика так – же будет однородным.
45. Поведение векторов В и Н на границе двух магнетиков:
![]()
![]() ®
®
n ®
B
![]()
![]()
![]() m1
m1
![]()
![]() b
b
m2
®
n
o BdS = -Bn1 S + Bn2 + BnSБОК = 0, где (BnSБОК ) = 0;
B1 n = B2 n
Компонента вектора индукции магнитного поля неприрывна.
m0 m1 H1 n = m0 m2 H2 n
![]()
![]() H1
n/H2
n = m2
/m1
H1
n/H2
n = m2
/m1
a1
![]()
![]()
![]() m1
I a
m1
I a
![]() b
b
m![]() 2
I
2
I
a2
m1 m2
® ®
oH dl = H1 t* a - H2 t* a + H* 2b = 0
H1 t = H2 t
B1 t/(m0 m1 ) = B2 t/(m0 m2 ) B1 t/B2 t = = m1 /m2
tg a1 /tg a2 = m1 /m2 .
46. Магнитные механические явления:
![]() Представлени
я Бора:
Представлени
я Бора:
![]()
![]() u
u
![]() ® ®
® ®
M r PM
![]()
![]()
![]()
е
I = en = e (w/2p) = e [u/(2pr)] – величина силы тока, создаваемого электронами.
L = Jw = mr2 * u/r = mur – механический момент. (m - ?)
Замена L ® M:
PM = IS = I* pr2 = (eur)/2 – магнитный момент.
PM /M = -l/(2m) – гиромагнитное отклонение.
M 0 – суммарный механический момент электронов.
-Mi 0 – суммарный механический момент атомов.
![]()
![]()
![]()
![]()
![]()
![]() Магнетик в магнитном поле приобретает отличные от нуля суммарные механические моменты атомов и электронов, в вследствие чего он начинает вращаться, что приводит к намагничиванию магнетика.
Магнетик в магнитном поле приобретает отличные от нуля суммарные механические моменты атомов и электронов, в вследствие чего он начинает вращаться, что приводит к намагничиванию магнетика.
 |
|||
 |
|||
![]()
![]()
Собственный механический момент:
~
MS = h/2 – этому кратен собственный механический момент для электрона.
~
h = h/2p = 1,05* 10– 34 (Дж* с)
Собственный механический момент (спин) равен половине постоянной Планка (h), которая играет роль элементарного магнитного импульса.
Собственный магнитный момент:
PMS /MS = - l/m;
~
PMS = - (l h)/(2m);
~
mБ = (l h)/2m – магнетон Бора.
Каждый атом, его магнитный момент складывается из орбитальных и силовых моментов электронов.
Было исследовано поведение атомов в магнитном поле:
F = PM (¶B/¶x) cos(a), a - угол между направлением магнитного момента и индукцией. Магнитные моменты атомов имеют произвольные углы ориентации.
48. Пара- и ферромагнетики:
У парамагнетиков магнитная восприимчивость немногим 0.
m у парамагнетиков мало отличается от 1.
У ферромагнетиков (железо, никель, кобальт и др.) магнитная восприимчивость » 1010 раз больше, чем у парамагнетиков.
У ферромагнетиков:
![]() J
J
 |
|
H
![]() B
B
![]() HC
HC
 |
BОБ
H
m
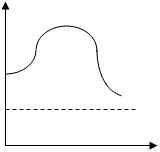 |
H
49. Электромагнитная индукция, ЭДС индукции, токи Фуко:
В электропроводящем контуре при изменении проходящего через него потока возникает ток, независящий от способа изменения потока, и называемый индукционным. В контуре так же возникает ЭДС.
IИНД = dФ/dt (скорость изменения потока).
Если контур заполнен магнетиком с проницаемостью m, то это приводит к увеличению потока в m раз.
Правило Ленца:
Индукционный ток I имеет такое направление, чтобы препятствовать причине, его вызывающей.
ЭДС индукции:
®
I
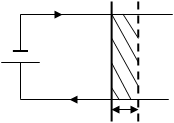
®
![]() (X) n ®
(X) n ®
e + R u
![]() ®
®
(X) B
®
I
DФ
Ie dt = dA – работа сторонних сил внутри источника.
Если R неподвижен, то dQ =I2 R dt – тепло, выделяющееся в R, dA = dQ.
Если R перемещается, то
dA = dQ + I dФ
eI dt = I2 R dt + I dФ
I = (e - dФ/dt)/R.
Поток магнитной индукции Ф измеряется в веберах (Вб).
ei = - dФ/dt.
Если витков несколько:
Ф ® y = N* Ф1
ei = -dy/dt = -N(dФ1 /dt), где y - потокосмещение.
При перемещении проводника с током:
![]()
![]() ®
®
(X) B
![]()
![]() (e)
(e)
![]() FИ
®
FИ
®
![]() U ®
U ®
u
®
FЛ
® ® ® ®®
dA = FЛ U dt + FИ u dt
dA = FЛ U dt - FИ u dt = e u B U dt - - e U B u dt = 0.
Токи Фуко:
Возникают в проводах, по которым текут переменные токи. Направлены они так, что ослабляют токи внутри провода и усиливают их внутри поверхности. В результате быстропеременный ток оказывается распределенным по сечению проводника неравномерно, он как бы вытесняется на поверхность проводника. Это явление называется скин – эффектом. Из-за него внутренняя часть в высокочастотных проводниках оказывается бесполезной, и обычно такие проводники представляют из себя трубки
Токи Фуко приводят к тепловым потерям. Используются в индукционных печах.
 |
50. Явление самоиндукции:
Если по проводнику течет ток, то его контур пронизывает магнитный поток.
Ф ® y (y - потокосмещение);
y ~ B ~ I ® y = L* I
L – коэффициент пропорциональности (индуктивность). Определяется геометрическими размерами контура, у ферромагнетиков еще и материалом среды.
Если контур жесткий и не может быть деформирован, то L – const.
Индуктивность солинойда:
B = m0 mnI (n – число витвов на единицу длины);
Ф = BS, y = ФN = m0 mnISnl = = m0 mn2 IV;
L = m0 mn2 V, где V – объем соленоида.
Возникает самоиндукция:
eS = -dy/dt = -(L* dI/dt + I* dL/dt) – ЭДС самоиндукции;
L – const, то eS = -L* dI/dt.
51. Энергия магнитного поля:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() L
L
R
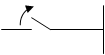 |
В центре всегда есть индуктивность, скорость установления тока всегда конечна.
dA = eS I dt = /- любая совершаемая работа/ = -dy/dt Idt = -dyI, где dy - величина изменения потока за время dt.
dy = L dI
dA = -LI dI;
A переходит в ленц - джоулевое тепло, выделяемое в проводах схемы.
0
A = dA = -L I dI = LI2 /2.
I0
L = m0 mn2 V
H = nI
A = W = LI2 /2 = 1/2* (m0 mH2 )* V
W – энергия маг. поля в соленоиде.
W/V = wH = 1/2* (m0 mH2 ) = BH/2 = = B2 /(2m0 m).
52. Уравнения Максвелла:
Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений, объяснившую многие из экспериментальных фактов и предсказала новые. Основным стал вывод о существовании электромагнитных волн, распространяющихся со скоростью света, что привело Максвелла к созданию электромагнитной теории света.
Основой теории стали уравнения Максвелла. Первую пару уравнений образуют:
[DE] = -¶B/¶t (связывает значение Е с изменениями вектора В во времени);
DВ = 0 (указывает на отсутствие источников магнитного поля, т.е. магнитных зарядов).
Вторая пара:
[DH] = j + ¶D/¶t (устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем);
DD = r (показывает, что источником вектора D служат сторонние заряды).
Для расчета полей нужно дополнить имеющиеся уравнения уравнениями, связывающими D и j c E, a так же H c B:
D = e0 eE;
B = m0 mH;
j = sE.
Перечисленные уравнения Максвелла и их дополняющие образуют основу электродинамики покоящихся сред.
Уравнения Максвелла в дифференциальной форме:
Первая пара:
оГ E dl = -d/dt S BdS (закон эл.-маг. индукции Фарадея, получается путем интегрирования ур-я в диф. форме с; последующим преобразованием левой части в интеграл с контуром Г, ограничивающему поверхность S)
oS BdS = 0 (отсутствие магнитных зарядов);
Вторая пара:
оГ Hdl = S jdS + d/dt S DdS (теорема полного тока);
oS DdS = V r dV (теорема Гаусса).
53. Вихревое электрическое поле. Токосмещение.
] проволочный контур, в котором индуцируется ток, неподвижен, а изменение магнитного потока происходит из-за изменения магнитного поля. Возникает индукционный ток, значит изменение маг. поля вызывают сторонние силы, вызываемые электрическим полем с напряженностью ЕВ .
ЭДС равна циркуляции ЕВ по контуру:
ei = oEB dl;
ei = -dФ/dt, то
oEB dl = -d/dlS BdS
oEB dl = -S (¶B/¶t)dS
S [EB ]dS = -S (¶B/¶t)dS, то
[EB ] = -¶B/¶t.
Поле ЕВ существенно отличается от порождаемого неподвижным зарядом поля Еq . Т.к. линии электрического поля начинается и заканчивается на зарядах, то [Eq ] = 0.
[EB ] 0 ® EB , как и магнитное поле, является вихревым.
Напряженность суммарного поля:
Е = EB + Eq ® [E] = -¶B/¶t.
Существование взаимосвязи между электрическими и магнитными полями говорит о том, что рассмотрение их по отдельности условно. Относительно одной инерциальной системы отсчета, заряды могут быть неподвижны, когда относительно другой они могут двигаться. Поле, которое относительно одной системы отсчета является только электрическим или только магнитным, относительно другой системы отсчета будет представлять собой совокупность электрического и магнитного полей, образующих единое электромагнитное поле.
Ток смещения:
Максвелл предположил, что $ обратная связь между полями.
+q -q
![]() ® ®
® ®
i D
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
S
jПР = /плотность тока в обкладках/ = = i/S = (q’( t) )/S = (q/S)’t = g’
D = g ® D’ = g’.
В пр-ве между пластинами при отсутствии тока проводимости, должен присутствовать ток смещения.
® ®
jCM = (D)’
Из всех св-в токопроводимости, ток смещения обладает только св-вом создавать магнитное поле. Ток смещения может быть создан полями любого вида. Он имеет место везде, где есть смещающееся электрическое поле.
® ® ® ® ®
j = jПР + jСМ = jПР + (D)’
® ® ® ® ® ®
oH dl = S jПР dS + S (dD/dt) dS.
54. Электромагнитные волны:
Существование электромагнитных волн вытекает из дифференциальных уравнений Максвелла, а именно соотношение:
® ®
DЕ = e0 em0 m(¶2 Е/¶t2 ) – волновое ур-е для Е.
e0 m0 = 1/С2 , где С – скорость распространения света.
® ®
DЕ = (em/С2 )* (¶2 Е/¶t2 );
При проецировании:
® ® ®
(¶2 Е/¶х2 ) + (¶2 Е/¶у2 ) + (¶2 Е/¶z2 ) =
®
= (em/С2 )* (¶2 Е/¶t2 );
® ® ®
(¶2 H/¶х2 ) + (¶2 Н/¶у2 ) + (¶2 Н/¶z2 ) =
®
= (em/С2 )* (¶2 Н/¶t2 );
1/u2 = em/С2 – фазовая скорость распростр анения волны в данной среде.
u = С/em;
Всякая функция Е или Н, удовлетворяющая вышеуказанным уравнениям описывает волну.
55. Плоская электромагнитная волна:
]$ плоская электромагнитная волна, распространяющаяся в нейтральной непроводящей среде.
g = 0; j = 0;
Волновая поверхность ^ оси x:
1) Вектора Е и Н ^ оси x и не зависят то координат y и z.
2) Электромагнитные волны когерентны, т.е. вектора Е и Н ^ направлению распространения.
3) Если считать ЕZ = 0, то HY = 0.
4) ¶2 EУ /¶x2 = (em/C2 )* (¶2 EY /¶t2 )
¶2 HZ /¶x2 = (em/C2 )* (¶2 HZ /¶t2 )
® ® ® ®
DE = (¶2 E/¶x2 ) + (¶2 E/¶y2 ) + (¶2 E/¶z2 ), где (¶2 E/¶y2 ) = (¶2 E/¶z2 ) = 0;
5) EУ = Em cos(wt – kx + a1 ); (m - ?)
HZ = Hm cos(wt – kx - a2 );
Вектора Е и Н колеблются в одной фазе, a1 = a2 . ___
6) Em* e0 e = H m* m 0 m ;__________
Em /Hm = m0 e0 = 4p* 10–7 * 9* 109 * 4p = = 120p;
® ®
E = Em cos(wt – kx);
® ®
![]()
![]()
![]()

![]() H = Hm
cos(wt – kx);
H = Hm
cos(wt – kx);
У
Х
Мгновенная фотография
Z
56. Энергия электромагнитных волн. Вектор плотности потока:
w = w E + wH = (e0 eE2 )/2 + ( m0 mH2 )/2 = 1/2(e0 e* E* m0 m* H + e0 e* m0 m* H* E = = (1/C)* E* H /e = 1, m = 1/ - объемная плотность энергии электромагнитного поля.
S = w* C – плотность потока энергии электромагнитного поля.
® ® ®
S = [E H] – определяет направление распространения энергии электромагнитного поля.
® ®
ФS = F S dF – кол-во энергии, переносимое через поверхность S за единицу времени.
В этом случаи Ленц – Джоулевое тепло выделяется за счет действия сторонних сил. При этом внутренняя энергия ни чем не поглощается и ни куда не выделяется.
E* rj, то на участке действия скоростных сил энергия электромагнитного поля будет выделяться в окружающее пространство и будет поглощаться обратно по всей длине проводника.
Любая цепь должна излучать электромагнитные волны.
57. Импульс электромагнитных волн:

![]() ®
®
![]() E ®
E ®
![]() j
j
fЕД.ОБ
®
Н
® ® ® ® ®
fЕД .ОБ = [j B] = m0 m [j H]
__
P = w , где w - величина плотности энергии, усредненная по времени; Р – давление. __
Р = (1 + k) w;
® ® ® ®
kЕД.ОБ = S/C2 = [E x H]/C2 , где k – импульс единицы объема.
kЕД.ОБ = mЕД.ОБ * C;
mЕД.ОБ = S/C3 = w/C2 , w - объемная плотность.
Е = mC2 ;
Все, что обладает энергией, обладает массой, любое изменение энергии приводит к изменению массы.
58. Световая волна:
Свет обладает дуализмом, т.е.проявляет те или иные св-ва в зависимости от методов наблюдения.
Волновые св-ва:
Вектор Е, его колебания:
E = A cos(wt – kr + a);
A = const;
A ~ 1/r, где r – и сточ ник волны.
n = C/u; n = em = e;
Имеет место явление дисперсии:
l = 0,40 0,76 мкм;
f = (0,39 0,75)* 1015 Гц.
Модуль плотности потока энергии, усредненного по времени, переносимой световой волной, называется интерференцией.
®
I = S;
Em e0 e = Hm m0 m;
S = EH ~ eE2 ~ I ~ eA2 .
Линии, вдоль которых распространяется световая энергия, называются лучами.
Естественный свет:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Возникает при высвечивании атомов. Атом переходит из возбужденного состояния в невозбужденное.
Возникает при высвечивании атомов. Атом переходит из возбужденного состояния в невозбужденное.
®
E
59. Интерференция света:
Модуль плотности потока энергии, усредненного по времени, переносимой световой волной, называется интерференцией.
®
I = S.
] две волны с одинаковой частотой возбуждают в некой точке пространства колебания одинакового направления.
E1 = A1 cos(wt + a1 );
E2 = A2 cos(wt + a2 );
A2 = A1 2 + A2 2 + 2A1 A2 cosd, где d = = a2 - a1 ; ___
I = I1 + I2 + 2I1 I2 cosd; (I - ?)
Если d не зависит от времени, то колебания когерентны.
cos[d(t)] = 0, если зависимость произвольная.
A1 = A2 ® I1 = I2 ;
d = 0 ® I = 4I;
d = -p ® I = 0;
Если колебания некогерентны, то I = 2I.
При интерференции происходит переораспределение световой энергии в пространстве.
n1
![]()
![]()
![]()
![]()
![]() 0
0
C
n2
wt – в точке 0, то в точке С колебания, возбужденные волной, прошедшей в n1 , будут
A1 cos[w* (t – S1 /u1 )];
A2 cos[w* (t – S2 /u2 )];
d = w* (S2 /u2 - S1 /u1 ) = = w/C* (S2 n2 – S1 n1 ) = // u = C/n; w/C = 2pf/C = 2p/l0 , где l0 – длина волны // = = (2p/l0 )* (S2 n2 – S1 n1 ) = = (2p/l0 )* D, где D - оптическая разность хода, S – путь в среде.
D* (2p/l0 ) = d;
DMAX = ±ml0 , m = 0, 1, 2, 3, …
d ~ m* 2p;
cos(d) = (m + 1/2)* 2p = (2m +1)* p - наблюдается минимум.
60. Интерференция двух щелей:
![]() Классический опыт:
Классический опыт:
l d
S1
![]()
![]() S2
S2
d/2
![]()
![]()
![]() d
d
![]() d/2 Dx
d/2 Dx
![]()
![]()
l
D = S2 – S1 ;
S1 2 = l2 + (x – d/2)2
S2 2 = l2 + (x – d/2)2
S2 2 - S1 2 = (S2 – S1 )(S2 – S1 ) = 2dx
S1 + S2 » 2* l, то
D = S2 – S1 = (2dx)/(2* l)
x = (D* l)/d
xMAX = (ml0* l)/(d* n) = m* (l/d)* l, (?)
где m = 0, ±1, ±2, ±3, …
l0 /n = l - длина волны в среде.
xMIN = (m + 1/2)* (l/d)* l
I1 = I2 = I0 (?)
I = 2I0 (1 + cos d) = 4I0 cos2 (d/2);
d ~ D ~ x, I ~ cos2 x;
Ширина максимума:
Dx = (l/d)* l
61. Интерференция тонких пленок:
![]()
![]() У толстых пленок интерференцию наблюдать невозможно.
У толстых пленок интерференцию наблюдать невозможно.
 q1
S1
q1
S1
![]()
![]() q1
q1
q1
q1
![]()
![]() n q2
q2
nS2
q2
n q2
q2
nS2
q2
d
![]()
S1 = 2d tgq2* sinq1
S2 = (2dn)/cosq2
D = nS2 – S1 = 2d* [(n2 – sinq1* sinq2* n)/(cosq2* n)] = = /sinq2* n = sinq1 / = = 2d[(n2 – sin2 q 1 )/(n* cos q 2 )] = = /n* cos q 2 = n2 – n2 * sin2 q2 / = = 2d* n2 – sin2 q1 ;
Учитывая потери при отражении от пленки: ________
D = 2d* n2 – sin2 q1 -l/2;
ml = D; _______
max: 2d* n2 – sin2 q1 = (m + 1/2)l, где m = 0, ±1, ±2, ±3, …
Условия mах и min при интерференциях в отраженном и проходящем свете меняются местами.
62. Кольца Ньютона:
![]()
![]()
![]()
![]() D = 2b + l/2
D = 2b + l/2
R
![]()
r
![]()
![]()
![]()
![]()
![]()
![]() b
b
R2 = (R + b)2 + r2 » /R b/ » » R2 – 2Rb + r2 ;
B = r2 /(2R);
D = r2 /R + l/2;
DMAX = ml = /m = 0, 1, 2, 3, …/ = = 2m* (l/2);
DMIN = (m + 1/2)l = (2m + 1)* (l/2);
r = m’lR, если m’ – четное, то условие минимума;
m’ – нечетное, то условие максимума.
63. Когерентность:
Согласование неких колебательных или волновых процессов называется когерентностью.
Степень когерентности – согласованность.
Состоит из цугов – наложенных друг на друга волн.
A cos(wt – kx + a)
A(t), w(t), a(t) – в реальной волне они так или иначе, но зависят от времени.
Интерференция может проявляться как то или иное св-во волны, в той или иной степени.
A1 cos[w(t)t + a1 (t)];
A2 cos[w(t)t + a2 (t)];
w(t) = w0 + Dw(t)
A2 = A1 2 + A2 2 + 2A1 A2 cos[d(t)];
d = a2 (t) - a1 (t) + Dw’(t);
Dw’(t) = Dw2 (t) - Dw1 (t).
64. Временная когерентность:
tПРИБ – время регистрации прибором (глазом) измеряемой величины.
d (t) = - p p;
cos[d(t)] = 0 – интерференция не наблюдает ся;
cos[d(t)] 0 – интерференция наблюдается.
tКОГ - время, за которое случайное изменение разности фаз складываемых колебаний не привышает p.
tКОГ tПРИБ – интерференция не наблюдается;
tКОГ tПРИБ – интерференция наблюдается;
tКОГ » tПРИБ – интерференция слаборазличима.
![]() Если щель большая, то колебания будут малосогласованными (некоге-рентными). Так же может не наблюдаться интерференция.
Если щель большая, то колебания будут малосогласованными (некоге-рентными). Так же может не наблюдаться интерференция.
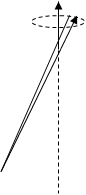
4. Поле линейного заряда:
![]()
![]()
![]() a
a
![]()
![]()
![]()
![]()
![]()
![]() У
У
![]()
![]() Х
Х
t da
r1 r R r2
![]()
![]() a1
a2
a1
a2
![]()
dl
![]() r*
dr
r*
dr
![]()
![]() a a
a a
![]()
dl
dl = (r* dr)/sina
r = R/sina
dl = (R* da)/sin2 a
dE = t* dl/(4pe0 r2 )
dEx = dE cosa = [t* dl/(4pe0 r2 )]* cosa= = [(tRda* sin2 a)/(sin2 a* 4pe0 R2 )]* cosa = = [t/(4pe0 R)]* cosa* da;
dEy = dE sina = [t/(4pe0 R)]* sina* da;
Ex = [t/(4pe0 R)]* a 1 a 2 cosada = = [t/(4pe0 R)]* (sina2 - sina1 );
Ey = [t/(4pe0 R)]* a 1 a 2 sinada = = [t/(4pe 0 R)]* (co sa1 - cosa2 );
E = E2 x + E2 y ;
Если нить бесконечна:
a1 = 0; a2 = 180;
Ex = 0; Ey = t/(2pe0 R).
10’. Уравнение Пуассона:
![]()
У
Ex dx Ex +(¶Ex /¶x)dx
dz
dy
Х
Z
ФХ = [Ex + (¶Ex /¶x)dx]dydz cos 0 + + EX dydz cos180;
ФX = (¶Ex /¶x)dxdydz = (¶Ex /¶x)dV;
ФУ = (¶EУ /¶y)dxdydz;
ФZ = (¶EZ /¶z)dxdydz;
oS EdS = ФХ + ФУ + ФZ = (¶Ex /¶x + + ¶EУ /¶y + ¶EZ /¶z)dV;
lim [(oS EdS)/V] = div E
V® 0
div E = (¶Ex /¶x + ¶EУ /¶y + ¶EZ /¶z)
По теореме Гаусса:
oS EdS = q/e0 e = (V rdV)/(e0 e);
divE = r/(e0 e);
divD = r.
24. Связанные заряды:
![]() + + + + + + + + + + + + + + + +
+ + + + + + + + + + + + + + + +
![]()
![]()
![]()
- -
![]()
![]()
![]()
![]()
![]() + +
+ +
+ - - -
+ +
![]()
E = E0 – EД
E0 /e = E0 - EД
EД = E0 (1 – 1/e) = E0 [(e - 1)/e]
e - 1 = c - диэлектрическая восприимчивость;
ЕД = Е0* (c/e);
ЕД = sД /e0 ;
Е0 = s/e0 ;
sД = s* (c/e), где sД – плотность заряда на диэлектрике;
s - плотность заряда на пластине конденсатора.
![]() 47. Диамагнетизм:
47. Диамагнетизм:
![]()
![]() PM
B
PM
B
![]() a
a
 ® ®
® ®
![]()
![]() u N
u N
![]()
a
® ®
![]()
![]()
![]() dM=Ndt
dM=Ndt
®
![]()
![]() M
M
Msina
![]()
![]() r’
r’
![]() ®
®
![]() I
I
PM
® ® ®
N = [PM B]
® ®
dM = N* dt
dM/(M* sina) = dj
N = PM* B* sina
|dM| = PM* B* sina* dt
(PM Bsina dt)/(Msina) = dj
dj/dt = wL – частота прецессии;
w = (PM /M)* B = (l/2m)* B, где В – величина непостоянная;
w не зависит от угла ориентации орбиты.
На е – орбите атомы прецессируют с одной частой.
Возникает дополнительный ток:
Происходит ослабление внешнего поля: PM ’ = I’pr’2 = e* (wL /2p)* pr’2 = = -(e2 /4m)* Br’2 ;
PM ’ = -(e2 /4m)* Br’2 = = -(e2 /6m)* Br;
r’2 = 2/3* r2 ;
i=1 N PM ’ = -(e2 /6m)Bi=1 N ri 2 ;
X = PM /(VH);
XМОЛ = [(-e2 * m0* NA )/(6m)]*I=1 N ri 2 .
Все вещества, атомы которых не имеют магнитного момента называются диамагнетиками. Их магнитная восприимчивость немногим 0.