Оптимальная частотно-временная фильтрация

СОДЕРЖАНИЕ: Методами обобщенного вариационного исчисления синтезирован частотно-временной фильтр, состоящий из перемножителя на известное опорное напряжение и включенного за ним стационарного фильтра.

канд. биологических наук М.П.Иванов, д-р техн. наук В.В.Кашинов

Санкт-Петербургский государственный университет

Методами обобщенного вариационного исчисления синтезирован частотно-временной фильтр, состоящий из перемножителя на известное опорное напряжение и включенного за ним стационарного фильтра. Показано, что корреляционный прием и согласованная фильтрация являются частными предельными случаями частотно-временного фильтра. При помощи понятия функции спектральной корреляции анализируется физический принцип работы частотно-временного фильтра. Показана возможность применения частотно-временного фильтра в спектральном дискриминаторе временных интервалов.

Структура некоторых приемных устройств, например, приемников американской спутниковой навигационной системы GPS, включает в себя коррелятор [1]. В корреляторе, являющемся оптимальным приемником при наличии белого шума (но не узкополосной помехи в виде расстроенной несущей [1]), осуществляется умножение входного процесса (сигнала и шума) на копию сигнала с последующим интегрированием. Поскольку существует еще возможность реализации оптимального приемника в виде согласованного фильтра, возникает вопрос, являются ли эти структуры оптимального приемника единственными?

Рассмотрим задачу частотно-временной фильтрации, которая заключается в умножении входного процесса на некоторое известное опорное напряжение (как и в перемножителе коррелятора), не уменьшающее энергию сигнала, и последующей линейной фильтрации (аналогично интегрированию в корреляторе) стационарным фильтром. Отклики частотно-временного фильтра на входной сигнал и шум можно представить в виде

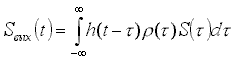(1)

и (2)

где - опорное напряжение; - импульсная переходная функция стационарного фильтра. Таким образом, ядра операторов (1,2) представлены в виде произведения k(t, t )=r (t )h(t-t ), где r - заданная известная функция, а h(t-t ) подлежит оптимизации.

При оптимизации будем использовать метод, разработанный в заметках [2-4]. В качестве критерия оптимальности выберем отношение сигнал-шум и представим значение полезного сигнала на выходе в момент максимума t₀ с помощью фильтрующего свойства d - функции в виде линейного функционала

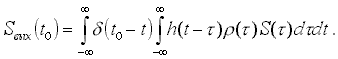(3)

Момент t₀ заранее неизвестен и принадлежит интервалу наблюдения T, а шум на выходе частотно-временного фильтра является нестационарным. Поэтому в качестве критерия оптимальности примем функционал I отношения пиковой мощности сигнала к средней по времени и по ансамблю мощности шума P_ш на выходе фильтра

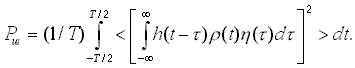(4)

Здесь и в дальнейшем угловые скобки T обозначают усреднение по ансамблю.

Поскольку сомножитель h(t-t ) в ядре операторов (1) и (2) - разностный, можно использовать свойство свертки и записать

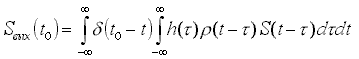(5)

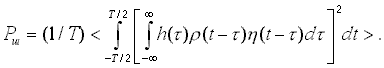и (6)

Таким образом, критерий оптимальности имеет вид

(7)

где S_вых (t₀ ) и P_ш выражаются формулами (5) и (6). Здесь уже можно применить методы обобщенного вариационного исчисления [2-4]. Обобщенное уравнение Эйлера-Пуассона для функционала (7) имеет вид

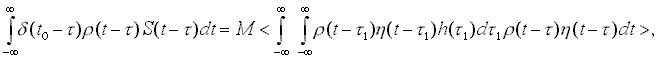(8)

где M - коэффициент пропорциональности, не влияющий на вид коэффициента передачи фильтра.

Переходя к спектрам и обозначая соответствие функций и их преобразований Фурье;;;, получаем выражение для коэффициента передачи стационарной инерционной части оптимального частотно-временного фильтра

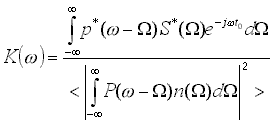(9)

где * обозначает комплексное сопряжение.

При любом выборе опорного напряжения r (t), которому соответствует спектр P(W ), не уменьшающем энергию сигнала, и любой помехи, в том числе и узкополосной, выводящей GPS из строя [1], существует коэффициент передачи K(w ) оптимального стационарного фильтра h(t ). Мощность множества пар r (t) и K(w ) может быть больше мощности континуума [3]. Даже для рассмотренного простейшего случая все ограничения для r (t) и K(w ) не определены. Из существования решений для частного случая задачи [3] следует существование множества ядер k(x,t), доставляющих функционалу (7) экстремум, причем значения этого экстремума для каждого k(x,t) из этого множества - одинаковые. Решением оптимизационной задачи будет конструктивное описание этого множества оптимальных ядер. Если r (t)=const, т.е. перемножитель отсутствует, P(w -W )=d (w -W ) и получается согласованный фильтр; если r (t)=S(t), получается коррелятор.

Таким образом, и корреляционный прием, и согласованная фильтрация являются частными предельными случаями частотно-временной фильтрации. Опорное напряжение r (t) и переходную функцию фильтра h(t-t ) следует выбирать, исходя из удобства реализации. А для осуществления оптимального приема при белом шуме применение коррелятора или согласованного фильтра обязательным не является.

Решение сформулированной задачи заведомо неоднозначное. Для описания этого множества потребуется использовать понятие функции спектральной корреляции.

Представляя знаменатель в выражении (9) в виде двойного интеграла и меняя порядок интегрирования и статистического усреднения, получаем

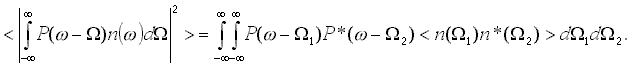(10)

Обозначим B(w ₁ ,w ₂ )=n(w ₁ )n*(w ₂ ); это выражение называется функция спектральной корреляции (ФСК) [5]. Если не учитывать свойства ФСК при мультипликативном воздействии на входной процесс, можно получить ошибочные результаты типа превышения потенциальной помехоустойчивости [6].

ФСК выражается через автокорреляционную функцию B(t₁ ,t₂ )

(11)

Средняя мгновенная мощность B(t₁ ,t₂ ) нестационарного процесса может быть выражена через ФСК

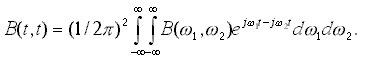(12)

Таким образом, вклад в мгновенную мощность нестационарного процесса вносит не только составляющая с частотой w , но и все коррелированные с ней. Это означает, что средние энергетические характеристики нестационарного процесса не локализуемы по частоте, откуда следует невозможность представления энергетических характеристик нестационарного процесса с помощью однократных интегралов в частотной области.

Средняя по времени спектральная плотность мощности нестационарного процесса может быть выражена через ФСК

(13)

Спектральная плотность нестационарного процесса характеризует вклад составляющих в интервале частот (w + dw ) и всех коррелированных составляющих с другими частотами.

Для стационарных процессов автокорреляционная функция зависит только от разности моментов времени t = t₁ vt₂ , и в этом случае

(14)

Для стационарных процессов все частотные составляющие некоррелированы.

При модуляции стационарного белого шума детерминированным опорным напряжением r (t) ФСК зависит только от разности частот

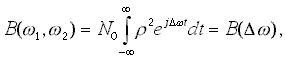(15)

где D w = w ₁ - w ₂ . Например, при стробировании стационарного белого шума периодической последовательностью импульсов средняя по времени спектральная плотность уменьшается в скважность раз; это можно наблюдать на экране анализатора спектра. Но появляется свойство, которое нельзя наблюдать на экране анализатора спектра - между спектральными составляющими появляется корреляция.

Парадокс. Предположим, что осуществляется оптимальный прием отрезка периодической последовательности импульсов на фоне белого шума. Как известно, оптимальным в данном случае является согласованный гребенчатый фильтр. Теперь включим на входе оптимального гребенчатого фильтра стробирующее устройство (перемножитель на последовательность прямоугольных импульсов единичной амплитуды) так, чтобы импульсы сигнала проходили без искажений. Спектральная плотность шума на выходе стробирующего устройства уменьшится в скважность стробов раз. Казалось бы, что отношение сигнал-шум на выходе гребенчатого фильтра должно увеличиться, но оно и так было максимально возможным, поскольку фильтр оптимальный. Разрешить парадокс помогает появление корреляции между спектральными составляющими. Ясно, что суммирование гребенок фильтра со сфазированными гармоническими составляющими сигнала и коррелированными составляющими шума результирующее отношение сигнал-шум не повысит.

Частотно-временная фильтрация может с успехом использоваться в спектральных дискриминаторах временных интервалов [7]. В некоторых радиоканалах, например, телеметрических каналах сверхдальней космической связи или GPS [1], отношение сигнал-шум оказывается P_с /P_ш 1. В таких каналах можно использовать временное уплотнение телеметрической информации путем передачи периодически повторяющихся пар импульсов для накопления, в интервале между которыми и заключается сообщение.

Способ дискриминирования отклонения временного интервала от заданного значения между импульсами периодической двухимпульсной последовательности (рис.1) заключается в следующем [7]. Огибающая амплитудного спектра (рис.2) такой последовательности находится в жесткой связи с интервалом между импульсами; сравнивая амплитуды определенных гармоник, можно судить о величине и знаке отклонения интервала t_инт между импульсами пары от заданного значения t ₀ .

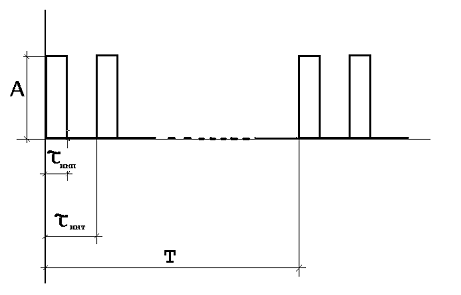
Рис. 1. Периодическая двухимпульсная последовательность.

Разложим временной процесс (рис.1) в тригонометрический ряд Фурье, т. е. вычислим спектр сигнала. При этом выражение для амплитуды n-й гармоники примет вид

(16)

где A - амплитуда импульсов; n - номер гармоники частоты повторения 1/T; T v период следования пар импульсов; t _имп - длительность импульсов; t _инт - длительность интервала внутри пар импульсов.

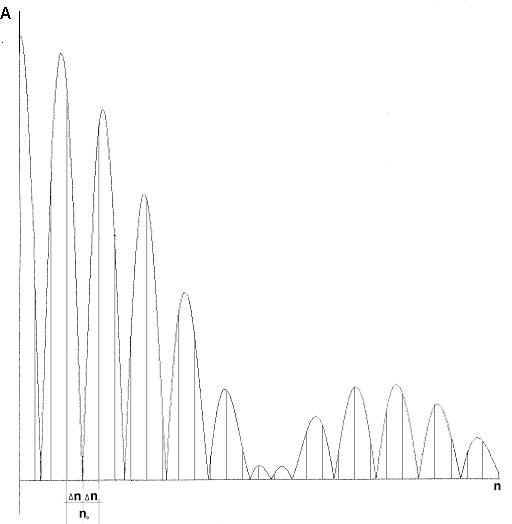
Рис. 2. Нормированная огибающая амплитудного спектра периодической двухимпульсной последовательности.

Огибающая спектра (рис.2) образуется произведением двух компонент: sin(p nt _имп /T)/p n, постоянного для данной последовательности и обусловленного формой импульсов, и cos(p n/T)t _инт , обусловленного интерференцией между одинаковыми по амплитуде, но отличающимися по фазе на угол j = 2(p n/T)t _инт гармониками отдельных импульсов в парах вследствие их сдвига во времени на величину t_инт (в пределах периода T/2). При изменении t _инт меняются амплитуды всех гармоник. Найдем номер гармоники n₀ , амплитуда которой изменяется быстрее других. Дважды продифференцировав второй сомножитель по t_инт и приравняв 2-ю производную нулю -cos(p n/T)t _инт =0, откуда номер оптимальной гармоники

n₀ = T/(2k-1)/2t₀ , k = 1,2,3, ... (17)

где t_инт = t ₀ + D t ; D t - отклонение интервала от заданного значения t ₀ . Оптимальные гармоники, имеющие максимальную скорость изменения амплитуды в зависимости от D t (максимальную крутизну), имеют нулевую амплитуду. Отклонение t _инт в любую сторону от t ₀ приводит к резкому увеличению амплитуды гармоники, а информация о знаке D t содержится в фазе гармоники. В этом случае выделение информации о знаке D t затруднительно.

Для определения величины знака отклонения проще не выделять оптимальную гармонику n₀ , а измерять разность амплитуд двух гармоник n₁ и n₂ , расположенных по обе стороны относительно провала в огибающей спектра сигнала n₀ . На рис.2 эти гармоники выделены: n₁ =n₀ vD n и n₂ =n₀ +D n.

При увеличении интервала t _инт относительно t ₀ провал в спектре, соответствующий n₀ при D t =0, смещается влево, к нулевой частоте, амплитуда гармоники n₁ уменьшается, а n₂ - увеличивается. При уменьшении t _инт все получается наоборот. Для компенсации первого сомножителя в формуле (16) при дальнейшей обработке амплитуды гармоник n₁ и n₂ можно выровнять.

Реализация предложенного способа может осуществляться при помощи устройства, состоящего из двух узкополосных фильтров, настроенных на гармоники n₁ и n₂ , выпрямителей и дифференциально включенного измерительного прибора. В этом случае напряжение сигнала на приборе можно представить

где q - коэффициент, зависящий от формы импульсов и затухания, вносимого первым множителем в формуле (16). При прямоугольных импульсах длительностью t _имп @ T(2m-1)/2n₀ , q ¦ 1.

Эту формулу можно преобразовать к виду

(18)

Учитывая, что D nn₀ , выражение для сигнала (18) можно приближенно представить

(19)

Из этой формулы следует, что чувствительность дискриминатора весьма высока. Возможность реализации высокой чувствительности, достигающей 0.001 мкс/мкА и выше, при относительно большой длительности импульсов (порядка единиц микросекунд) объясняется близостью и сравнительно небольшим номером используемых гармоник (малой величиной D n), когда изменения формы или длительности импульсов сказываются на амплитудах обеих гармоник практически одинаково.

Если на вход индикаторного прибора, кроме сигнала, поступает флюктуационный шум с дисперсией s ² _ш , то дисперсия ошибки измерения отклонения s ² _t составит

(20)

Шум на индикаторном приборе формируется как разность амплитуд спектральных составляющих, выделенных неперекрывающимися фильтрами с одинаковыми полосами пропускания из входного белого шума. Мощность шума на приборе в этом случае можно представить

где R(2D n) - коэффициент спектральной корреляции при разносе номеров гармоник 2D n. Если s ₁ = s ₂ = s , получим

(21)

Если входной шум не стробируется, то R(2D n) = 0 и s ² _ш = 2s ² .

Если на входе дискриминатора включен стробирующий каскад спектральная плотность мощности шума уменьшится в число раз, равное скважности стробов Q. Кроме этого, появится спектральная корреляция, что приведет к дополнительному уменьшению мощности шума за счет вычитания взаимокорреляционного компонента.

Предложенный дискриминатор реализует совмещение измерительных схем и накопителей в одном узле: узкополосные фильтры, выделяющие гармоники, являются фазочувствительными элементами и накопителями одновременно. Здесь же реализуется частотно-временной фильтр в виде стробирующего каскада, узкополосных фильтров и вычитающего устройства. Не следует думать, что, поскольку используются только две гармоники, остальные излучаются напрасно, и их энергия пропадает. Эти, не используемые напрямую гармоники, позволяют осуществлять импульсное излучение и стробирование при приеме импульсов. Стробирование сокращает время воздействия шума и, следовательно, его энергию, а появление спектральной корреляции еще больше уменьшает мощность шума на выходе вычитающего устройства.

Появление спектральной корреляции при нестационарной фильтрации должно учитываться при анализе работы нестационарных фильтров, а также может быть с успехом использовано при конструировании самых различных устройств.

Список литературы

Иванченко В.И. Теория и практика падающих томагавков // Компьютерра, 2000, ¦34. С. 24-33.

КашиновВ.В., Оганджанянц С.И. Необходимые условия оптимальности в разрывных задачах управления и фильтрации // АиТ, 1966, ¦ 1, С. 85-93.

Кашинов В.В. О множестве частных необходимых условий оптимальности в разрывных задачах нестационарной фильтрации // АиТ, 1988, ¦ 2, С. 177-178.

Кашинов В.В. Необходимые условия оптимальности для разрывных задач линейной нестационарной фильтрации // АиТ, 1999, С. 186-188.

Фельдман Ю.И., Мандуровский И.А. Теория флуктуаций локационных сигналов, отраженных распределенными целями // М.: Радио и связь, 1988.

Громов Г.Н. Преобразование сигналов дифференциально-геометрическим методом // Радиотехника, 1989, N 5, C.93-96.

Кашинов В.В., Мищенко Е.П. А.С. 1032912 от 11.10.1965.

Скачать архив с текстом документа