Проекция вектора на ось
СОДЕРЖАНИЕ: Содержание: Введение 3 Значение вектора и скаляра .4 Определение проекции, оси и координатой точки ...5Содержание:
Введение…………………………………………………………………………3
1. Значение вектора и скаляра………………………………………….4
2. Определение проекции, оси и координатой точки………………...5
3. Проекция вектора на ось……………………………………………...6
4. Основная формула векторной алгебры……………………………..8
5. Вычисление модуля вектора по его проекциям…………………...9
Заключение……………………………………………………………………...11
Литература……………………………………………………………………...12
Введение:
Физика неразрывно связана с математикой. Математика дает физике средства и приемы общего и точного выражения зависимости между физическими величинами, которые открываются в результате эксперимента или теоретических исследований.Ведь основной метод исследований в физике – экспериментальный. Это значит – вычисления ученый выявляет с помощью измерений. Обозначает связь между различными физическими величинами. Затем, все переводится на язык математики. Формируется математическая модель. Физика - есть наука, изучающая простейшие и вместе с тем наиболее общие закономерности. Задача физики состоит в том, чтобы создать в нашем сознании такую картину физического мира, которая наиболее полно отражает свойства его и обеспечивает такие соотношения между элементами модели, какие существуют между элементами.
Итак, физика создает модель окружающего нас мира и изучает ее свойства. Но любая модель является ограниченной. При создании моделей того или иного явления принимаются во внимание только существенные для данного круга явлений свойства и связи. В этом и заключается искусство ученого - из всего многообразия выбрать главное.
Физические модели являются математическими, но не математика является их основой. Количественные соотношения между физическими величинами выясняются в результате измерений, наблюдений и экспериментальных исследований и лишь выражаются на языке математики. Однако другого языка для построения физических теорий не существует.
1. Значение вектора и скаляра.
В физике и математике вектор - это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким, как масса, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они скалярами .
Они записываются либо буквами обычного шрифта, либо цифрами (а, б, t, G, 5, 7….). Скалярные величины могут быть положительными и отрицательными. В то же время некоторые объекты изучения могут обладать такими свойствами, для полного описания которых знание только числовой меры оказывается недостаточным, необходимо ещё охарактеризовать эти свойства направлением в пространстве. Такие свойства характеризуются векторными величинами (векторами). Векторы, в отличие от скаляров, обозначаются буквами жирного шрифта: a, b, g, F, С ….
Нередко вектор обозначают буквой обычного (нежирного) шрифта, но со стрелкой над ней: ![]()
Кроме того, часто вектор обозначают парой букв (обычно заглавных), причём первая буква обозначает начало вектора, а вторая - его конец.
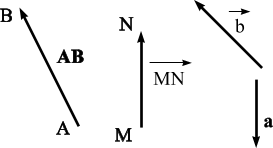
Модуль вектора, то есть длину направленного прямолинейного отрезка, обозначают теми же буквами, как и сам вектор, но в обычном (не жирном) написании и без стрелки над ними, либо точно также как и вектор (то есть жирным шрифтом или обычным, но со стрелкой), но тогда обозначение вектора заключается в вертикальные черточки.
Вектор – сложный объект, который одновременно характеризуется и величиной и направлением.
Не бывает также положительных и отрицательных векторов. А вот равными между собой векторы быть могут. Это когда, например, aиb имеют одинаковые модули и направлены в одну сторону. В этом случае справедлива запись a = b. Надо также иметь в виду, что перед символом вектора может стоять знак минус, например, - с, однако, этот знак символически указывает на то, что вектор -с имеет такой же модуль, как и вектор с, но направлен в противоположную сторону.
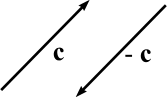
Вектор -с называют противоположным (или обратным) вектору с.
В физике же каждый вектор наполнен конкретным содержанием и при сравнении однотипных векторов (например, сил) могут иметь существенное значение и точки их приложения.
2.Определение проекции, оси и координатой точки.
Ось
– это прямая, которой придается какое–то направление.
Ось обозначается какой-либо буквой: X , Y , Z , s , t … Обычно на оси выбирается (произвольно) точка, которая называется началом отсчета и, как правило, обозначается буквой О. От этой точки отсчитываются расстояния до других интересующих нас точек.
Проекцией точки
на ось называется основание перпендикуляра, опущенного из этой точки на данную ось. То есть, проекцией точки на ось является точка.
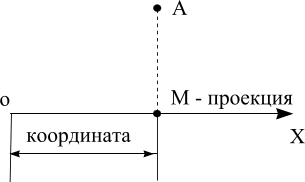
Координатой точки
на данной оси называется число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между началом оси и проекцией точки на эту ось. Это число берется со знаком плюс, если проекция точки располагается в направлении оси от ее начала и со знаком минус, если в противоположном направлении.
3.Проекция вектора на ось.
Проекцией вектора на ось называется вектор, который получается в результате перемножения скалярной проекции вектора на эту ось и единичного вектора этой оси. Например, если аx
– скалярная проекция вектора а на ось X, то аx
·i - его векторная проекция на эту ось.
Обозначим векторную проекцию также, как и сам вектор, но с индексом той оси на которую вектор проектируется. Так, векторную проекцию вектора а на ось Х обозначим аx
(жирная буква, обозначающая вектор и нижний индекс названия оси) или ![]() (нежирная буква, обозначающая вектор, но со стрелкой наверху (!) и нижний индекс названия оси).
(нежирная буква, обозначающая вектор, но со стрелкой наверху (!) и нижний индекс названия оси).
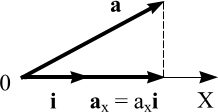
Скалярной проекцией
вектора на ось называется число
, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Обычно вместо выражения скалярная проекция
говорят просто – проекция
. Проекция обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектора,
то его проекция обозначается аx
. При проектировании этого же вектора на другую ось, если ось Y , его проекция будет обозначаться аy
.
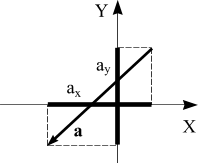
Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть
аx = хк xн .
Проекция вектора на ось - это число. Причем, проекция может быть положительной, если величина хк больше величины хн ,
отрицательной, если величина хк меньше величины хн
и равной нулю, если хк равно хн .

Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.
Из рисунка видно, что аx
= а Cos
то есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора
. Если угол острый, то
Cos 0 и аx
0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна.
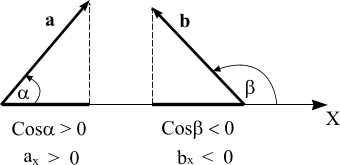
Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу - отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos = Cos ( ), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против.
Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.
4. Основная формула векторной алгебры.
Спроектируемвектор а на оси Х и Y прямоугольной системы координат. Найдем векторные проекции вектора а на эти оси:
аx = аx ·i, аy = аy ·j.
Но в соответствии справилом сложения векторов
а = аx + аy .
Или
а = аx ·i + аy ·j.
Таким образом, мы выразили вектор через его проекции и орты прямоугольной системы координат (или через его векторные проекции).
Векторные проекции аx
и аy
называютсясоставляющими или компонентами вектора а. Операция, которую мы выполнили, называется разложением вектора по осямпрямоугольной системы координат.
Если вектор задан в пространстве, то
а = аx
·i + аy
·j + аz
·k.
Эта формула называется основной формулой векторной алгебры. Конечно, ее можно записать и так:
а = аx + аy + аz .
5.Вычисление модуля вектора по его проекциям.
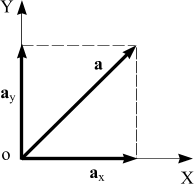
Пусть на плоскости задан вектор а .

Опустим с начала и конца вектора перпендикуляры на координатные оси для нахождения его проекций. В соответствии с теоремой Пифагора ![]() .
.
Отсюда
![]() .
.
Чтобы найти модуль вектора надо извлечь корень квадратный из суммы квадратов его проекций .
Проекцию вектора на ось можно найти, если из координаты точки конца вектора вычесть координату точки его начала. Тогда для нашего вектора, если он задан на плоскости, аx
= хк
хн
,
аy
= yк
yн
.
Следовательно, модуль вектора можно найти по формуле
![]() .
.
Ведь модуль вектора – это длина отрезка, заключенного между двумя точками: точкой начала вектора и точкой его конца - расстояние между двумя этими точками. Поэтому чтобы найти расстояние между любыми двумя точками, нужно вычислить модуль вектора, соединяющего эти точки.
Заключение:
Не следует думать, что всякая физическая величина, имеющая направление, обязательно является вектором. Электрический ток имеет направление, но это не вектор. Углу тоже придается направление (мы углы отсчитываем либо по ходу часовой стрелки, либо-против), но и угол - не вектор.
Главным признаком того, что данная величина есть вектор является то, что, если она с себе подобной складывается геометрически (например, по правилу параллелограмма), и в результате такого сложения мы получим величину, истинность которой подтверждается экспериментом, то, значит, складываемые величины - векторы.
Таким образом, вектором называют величину, характеризуемую числовым значением, направлением в пространстве и складывающейся с другой, себе подобной величиной геометрически.
Литература:
1. «Коллекция курсов по физике» Н. С.Чернов, Москва -2009год.
2. «Курс общей физики.» Механика. Александров Н.В., Яшкин А.Я. М.: Просвещение, 1978 год.
3. «Курс общей физики» т.1-3, Савельев И.В. Москва- 2006 год.