Проектування тренду

СОДЕРЖАНИЕ: Ознайомлення зі змістом методу прогнозування тренду за середнім рівнем, на основі абсолютного приросту та темпу росту за останній рік. Визначення загального вигляду згладжуючого рівняння для одержання середніх та розрахункових значень випадкових величин.

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

КРИВОРІЗЬКИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

Кафедра економіки, організації та управління підприємствами

КОНТРОЛЬНА РОБОТА

з дисципліни Економічне прогнозування

Виконав: ст. гр. ЗЕП-05-2

Плюсніна Г.О.

Перевірив

Буханець В.В.

Кривий Ріг - 2010

ЗМІСТ

1. Теоретичне питання: Метод проектування тренду

2. Практичне завдання Прогнозування за показниками динаміки ряду

3. Практичне завдання Прогнозування на основі аналізу тренду

4. Використані джерела

1. Теоретичне питання: Метод проектування тренду

Тренд - це тривала тенденція зміни економічних показників. Під трендом розуміється характеристика основної закономірності руху в часі, у деякій мірі вільної від випадкових впливів. При розробці моделей прогнозування тренд виявляється основною складовою прогнозованого часового ряду, на яку вже накладаються інші складові. Результат при цьому повязується винятково з плином часу. Передбачається, що через час можна виразити вплив усіх основних чинників. Метод проектування тренду полягає у тому, щоб екстрапольовану частину загальної кривої розвитку (тренда) коректувати з урахуванням реального досвіду розвитку галузі -аналога чи обєкта, що випереджають у своєму розвитку прогнозований обєкт. Метод проектування тренду звичайно припускає, що розпочата зміна перемінної триватиме у майбутньому. На цьому ґрунтуються принципи прогнозування тренда з використанням регресійного аналізу. Подібним чином часто проектуються обсяг продажу, валовий національний продукт і т.п. Коли прогнози засновані на проекції минулих трендів, тренд може бути простою незваженою прямою або операція зважування може бути здійснена лише щодо останнього, найважливішого періоду, а більш давнім періодам, як правило, приділяється значно менше уваги. Безсумнівно, найбільш широко розповсюдженим методом виявлення тренда часових рядів є регресійний аналіз, а саме - метод найменших квадратів. Для обчислення параметрів рівняння виду частіш за все користуються методом найменших квадратів. При цьому ставиться умова, щоб сума квадратів відхилень (відстаней) всіх досліджених точок від ординат, обчислених за рівнянням прямої _i, була мінімальною. Іншими словами, пряма повинна проходити якомога ближче до вершин емпіричної лінії регресії. Це означає, що параметри k і b управління регресії треба визначити з рівняння:

, (1.1)

де y_i – ординати досліджуваних точок;

– ординати розрахункових точок, визначені за рівнянням регресії =к х_i + b, таким чином .

Умовою екстремуму даної функції слід вважати рівність нулю часткових виробничих, узятих за параметрами k і b

звідси 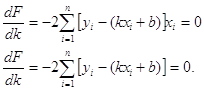(1.2)

Скоротивши на (-2) і розкривши квадратні дужки, отримаємо систему лінійних рівнянь

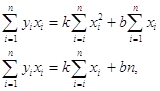(1.3.)

Підставивши сюди чисельні значення відповідних величин, знайдемо параметри k і b .

У разі лінійної залежності геометричне і алгебраїчне значення коефіцієнта регресії полягає в тому, що він кількісно характеризує на скільки в середньому змінюється у при зміні x_i на одиницю свого вимірювання. Чим більше чисельні значення коефіцієнта регресії, тим більше відносний приріст функції при зміні аргументу.

При знаходженні параметрів параболи виду необхідно складати і вирішувати систему з трьох нормальних рівнянь, яке розв’язується, виходячи з вимоги методу найменших квадратів, тобто .

Підставляючи , маємо

(1.4)

Знаходимо часткові похідні і прирівнюємо їх до нуля

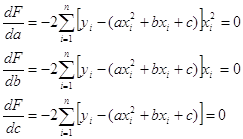(1.5)

Після відповідного перетворення маємо

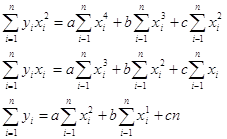(1.6)

Не важко помітити, за яким правилом складається система нормальних рівнянь для знаходження невідомих параметрів шуканої функції.

Моделі трендів зі змінним успіхом використовувалися в минулому. Прогнози на 1929, 1933, 1937, 1973 і 1980 pоки виявилися згубними для американських компаній, що повірили трендам попередніх років. Проте, метод й надалі широко використовувався, тому що більшість економічних часових рядів унаслідок притаманних їм кумулятивних властивостей дійсно показують стійку тенденцію до зміни в тому ж напрямку в найближчому майбутньому. Отже, прогнози на основі проектування трендів з більшою імовірністю будуть виконуватися до точки зміни напрямку, ніж не виконуватися.

На жаль, метод проектування трендів не може визначити зміни в їх напрямку, але ж саме ці поворотні точки особливо важливі в практиці менеджменту. Якщо поворотні точки можуть бути виявлені заздалегідь, то керівництво фірми може змінити свої плани щодо обсягу продажу, виробництва, кредитування тощо. У протилежному випадку просте проектування тренда дає прогноз на продовження, а не на зміну політики фірми.

Коли тренд і сезонні зміни вилучені з річного ряду економічних даних, починають виявлятися флуктуаційні характеристики, названі економістами циклами ділової активності (чи бізнес-циклами). Розвиток світової економіки вніс важливі зміни в структурні економіки держав, регіонів і відповідно змінив діловий цикл. Проте використання циклічних моделей прогнозування продовжується в багатьох фірмах. Найчастіше при створенні прогнозних моделей застосовуються мультиплікативні структури, де звязок між перемінними виражається формулою

О = T S C I,

де О - загальна тенденція; Т - тренд; S - сезонні зміни; С - циклічні зміни, а І - іррегулярні сили.

Завдання полягає в тому, щоб ізолювати і виміряти окремо кожний з цих чотирьох чинників шляхом виділення із загальної тенденції постійної довгострокової зміни Т; регулярних коливань S, що відбуваються протягом усього року; і регулярних коливань С, що відбуваються через кілька років. Однак ця проблема взаємозвязків між перемінними відступає на другий план у порівнянні з такими труднощами вимірювання:

1. При дослідженні циклічного механізму як для економіки в цілому, так і для окремої фірми, виникає сумнів щодо правильності методу аналізу. Аналітики довели, що в рядах можуть бути присутні окремі цикли, але не тому, що ці цикли дійсно існують, а просто таким чином представлена інформація. Наприклад, використання ковзного середнього може викликати появу коливань у підсумковому ряді, навіть якщо не існує реального циклу. У загальному випадку вже саме підсумовування чи усереднення послідовних значень випадкового ряду може викликати появу циклічних змін {так званий, ефект Слуцького-Иула). Тому звичайні методи аналізу відхилень, що застосовуються більшістю фірм для поділу циклічних і випадкових компонентів часових рядів, ніяким чином не є універсальними для всіх випадків. Навпаки, їх правильність піддається критиці аналітиками упродовж багатьох років.

2. Поділ тренда і випадкових сил, що діють у часовому ряді, також під сумнівом. Різні дослідження часових рядів говорять про те, що, цілком імовірно, тренд не молена відокремити від короткострокових змін у ряді і що, можливо, ці явища викликані тими самими силами. Якщо інтервал між даними в ряді малий, то випадкові відмінності між сусідніми членами можуть бути досить великі для того, щоб переважити будь-який систематичний ефект, так що виявиться, що дані ведуть себе майже як блукаючий ряд. Якщо ряд дійсно блукає, то будь-яка зміна, що здається систематичною, наприклад тренд чи цикл, є ілюзія, і поділ і вимір цих явищ ризикований. На жаль, за допомогою статистичних методів складно відрізнити дійсно блукаючі ряди від рядів зі слабкою систематизацією.

Ясно, що механічні методи обробки часових рядів - методи, які широко застосовуються багатьма фірмами, мають цілий ряд обмежень. Проте це не означає, що такі методи мають бути усунені з практики. Вони застосовуються в певних випадках і дуже часто використовуються як складова частина набору аналітичних інструментів економіста. Обмежені можливості, цих методів, розглянуті раніше, виявляються лише тоді, коли ці методи використовуються як єдиний інструмент прогнозування. При правильному використанні традиційних методів аналізу часових рядів вони мають такі переваги:

1.Необхідна інформація є мінімальною і легко доступною, її одержують або від самої компанії, або зі сторонніх джерел.

2.Аналітичні розрахунки, такі, як розрахунок ковзних середніх, як правило, досить прості і мають стандартну форму, тому зручні для обробки на компютері. Таким чином, ці способи особливо добре підходять для розвязання проблем, в яких необхідне прогнозування багатьох перемінних.

3.Економістам досить мати лише базові навички. Самі методи дуже прості, а дані обробляються в первісному вигляді.

4.Ці методи, як правило, обєктивні, хоча при виборі фіксованих чи сезонних змінних факторів (типу тренда й екстраполяції циклічної перемінної) і потрібен субєктивний підхід.

5.Результати прогнозів звичайно є досить точними для короткострокового прогнозування, скажімо, на 12 місяців. Аналіз часових рядів звичайно допускає проведення розрахунку погрішності прогнозування. Довірчий інтервал передбачених значень підвищує якість прогнозу. Помилки прогнозування надалі можуть бути зменшені, якщо є можливість виявити залежний тренд і сезонні зміни. Якщо виконано розкладання часових рядів, то можна зробити звичайний аналіз окремих компонентів.

Незважаючи на зазначені переваги, аналіз часових рядів, як і будь-який інструмент, повинен застосовуватись із урахуванням його обмежень:

1. Аналіз часових рядів не може бути використаний при недостатності даних у рядах (наприклад, для нового продукту чи нового обладнання, для яких ще не накопичена ретроспективна інформація, не можна виконати проектування тренда).

2. Прогнози, засновані на екстраполяції тренда, а також циклічних і сезонних компонент рядів, мають сильну схильність до проекції на майбутнє старих схем. Це не завжди виявляється правильним.

3. Сильна прихильність до техніки аналізу часових рядів поступається перед прогнозом перспектив майбутнього розвитку. Наприклад, економіст може знати, що витрати на рекламу в майбутньому збільшаться, і це знання дозволяє йому змінити екстраполяцію.

4. Аналіз часових рядів не дає інформації про випадкові чинники, що впливають на компоненти рядів. Він просто дає базу для імовірнісного аналізу.

2. Практичне завдання Прогнозування за показниками динаміки ряду

Табл. 2.1 Вихідні дані

Показник	Роки
Показник	1996	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006
Рентабельність, %	0,92	0,89	0,9	0,91	0,77	0,86	0,84	0,79	0,76	0,74	0,72

1) Прогнозування за середнім рівнем

Прогнозування за середнім рівнем полягає в тому, що за прогнозоване значення у_t :

де n – кількість спостережень;

у_і – спостерігаєме значення рівня динамічного ряду.

Допустима похибка прогнозу визначається за формулою:

у = t* ,

t – довірчий коефіцієнт, що вибирається в залежності від рівня надійності (Р).

При

Р 68% t=1

P 95% t=2

P 98% t=3

– середня квадратична похибка обчислюється таким чином:

Довірчий інтервал прогнозованого значення показника знаходиться в межах:

нижній рівень: y_н = _t - у ; верхній рівень: y_в = _t + у .

Визначимо середнє значення ряду динаміки:

Обчислимо середню квадратичну похибку:

З надійністю 95% прогнозоване значення рентабельності буде коливатися в межах:

у_н = 0,83 - 2*0,07 = 0,69%

у_в = 0,83 + 2*0,07 = 0,97%

2) Прогнозування на основі абсолютного приросту за останній рік (метод від досягнутого).

Абсолютний приріст показника характеризує абсолютний розмір збільшення (зменшення) рівня ряду за певний проміжок часу і обчислюється як різниця між двома рівнями ряду.

Прогнозування за цим методом здійснюється так:

1) на підставі вихідних даних визначається абсолютний приріст за останній рік (різниця між значенням за останній та попередній роки).

у=у_n -y_n-1

2) визначається прогнозоване значення показника через t років:

y_t+t =y_t + t· y ,

де у_t – значення показника ряду за останній рік;

t – кількість років прогнозу.

Визначимо абсолютний приріст за останній рік:

у = 0,72 – 0,74 = -0,02%

Прогнозоване значення показника рентабельності через 3 роки становить:

У₂₀₀₈ = 0,72 + 3*(-0,02) = 0,66%

3) Прогнозування за середнім абсолютним приростом

Середній абсолютний приріст ( ) – показник, що оцінює на скільки одиниць у середньому збільшується (зменшується) рівень ряду динаміки порівняно з попереднім за одиницю часу:

Прогнозоване значення показника через t років визначається за формулою:

У_t+t = y_n + t·

Визначимо середній абсолютний приріст:

Прогнозоване значення показника рентабельності через 3 роки дорівнює:

У₂₀₀₈ = 0,72 + 3· (-0,02) = 0,66%

4) Прогнозування на основі темпу росту за останній рік (метод від досягнутого).

Темп росту (К) показує, у скільки разів рівень росту динаміки більший (менший) за інший рівень ряду.

Прогнозування на підставі темпу росту здійснюється так:

1) на підставі вихідних даних обчислюється темп росту значення показника за останній рік:

де y_n – значення показників за останній рік;

y_n-1 - значення показників за попередній рік.

2) знаходиться прогнозоване значення показника через t років:

у_t+t = y_n ·K^t

Обчислимо темп росту показника рентабельності за останній рік:

Прогнозоване значення показника рентабельності через t=3 роки дорівнює:

У₂₀₀₉ = 0,72·(0,97)³ 0,66%

5) Прогнозування за середнім темпом росту

Середній темп росту () – це показник, що оцінює у скільки разів у середньому збільшується (зменшується) рівень ряду динаміки порівняно з попереднім за одиницю часу.

Прогнозоване значення показника t років обчислюється за формулою

У_t+t = y_n ()^t

Визначимо середній темп росту показника рентабельності:

Прогнозоване значення показника рентабельності через t =3 роки дорівнює:

У₂₀₀₉ = 0,72*(0,98)³ 0,67%

6) Прогнозування за темпом приросту для останнього року

Темп приросту Т – це показник, що характеризує, на скільки одиниць один рівень ряду динаміки більший (менший) за інший рівень:

Прогнозоване значення показника через t років обчислюється так:

Розрахуємо темп приросту:

Прогнозоване значення показника рентабельності через t=3 роки дорівнює:

3. Практичне завдання Прогнозування на основі аналізу тренду

Табл. 3.1 Вихідні дані

Показник	Роки
Показник	1996	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006
Рентабельність, %	0,92	0,89	0,9	0,91	0,77	0,86	0,84	0,79	0,76	0,74	0,72

Перше наближення до очікуваної в майбутньому прогнозованої величини дає прогнозування на основі визначеної тенденції (тренду), що показує загальне спрямування розвитку досліджуваного процесу. Тенденція (тренд) – це лінія регресії (або лінія згладжування) в динамічних рядах. Якщо у(х) – випадкові величини, розподіл яких залежить від часу х, то трендом називають таку функцію у(х), значення якої в інтервалі здійснених спостережень у кожній точці х дорівнюватиме середньому значенню ў(х)

Для одержання середніх, або розрахункових значень ў(х), необхідно визначити загальний вигляд згладжуючого рівняння (або рівняння тренду), яке в свою чергу визначається за виглядом згладжуючої лінії (лінії тренду). Для цього будується графік динаміки розвитку показника, потім проводиться лінія тренду.

В нашому прикладі графік динаміки та лінія тренду мають такий вигляд:

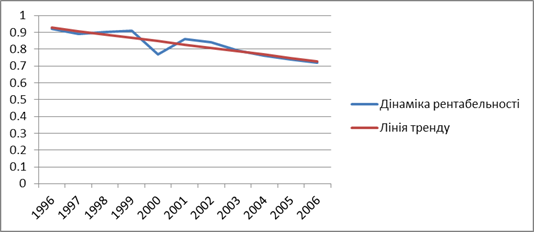
Рис. 1. Графік динаміки розвитку показника та лінія тренду

Тобто, для нашого прикладу рівняння тренду має вигляд:

у(х) = а₀ + а₁ х,

де а₀ = 0,9467, а₁ = – 0,0199 - параметри рівняння тренду.

У = 0,9467-0,0199х

По отриманому рівнянню проводимо розрахунки значень показника за кожний рік, а також відхилення фактичних значень від розрахункових. З метою спрощення розрахунків роки (х) взяті як числа 1, 2, 3, … ,11.

результати розрахунків заносимо в табл. 2.

Таблиця 3.2 Фактичні та розрахункові значення показника рентабельності виробництва (%)

Показник	Роки
Показник	1996	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006
Рентабельність фактична, у_і	0,92	0,89	0,9	0,91	0,77	0,86	0,84	0,79	0,76	0,74	0,72
Рентабельність розрахункова, ў	0,927	0,907	0,887	0,867	0,847	0,827	0,807	0,788	0,768	0,748	0,728
Абсолютне відхилення, t	-0,007	-0,017	0,013	0,043	-0,077	0,033	0,033	0,003	-0,008	-0,008	-0,008
Відносне відхилення, , %	0,7	1,9	1,5	4,9	9,1	4,0	4,0	0,3	1,0	1,0	1,1

На підставі отриманих розрахунків проводимо візуальну оцінку практичної доцільності рівняння тренду, тобто відзначаємо на мал. 2.1 розрахункові значення показника і порівнюємо отриману лінію з попередньо визначеною лінією тренду. В нашому випадку ці лінії співпадають.

Далі проводимо розрахунки загальних показників прогнозних значень:

1) Середня лінійна похибка

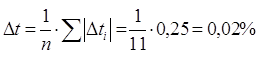
2) Середня відносна похибка

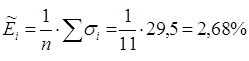
3) Середня квадратична похибка

4) Гранична похибка за умови, що рівень надійності 95%

_гр = t· =2·0,06=0,12%

Для 2009 року отримуємо середнє значення у:

У₂₀₀₉ = 0,9467 - 0,0199 * 14 = 0,67%

Довірчий інтервал прогнозованого значення показника буде знаходитися в межах:

у _нижнє = 0,67 – 0,12 = 0,55%

у _верхнє = 0,67 + 0,12 = 0,79%

Тобто, прогнозоване значення показника рентабельності виробництва буде коливатися в межах від 0,55 до 0,79, а його середні значення буде дорівнювати 0,67%.

Перевагою цього методу є те, що він ураховує період упередження, а недоліками – те, що кожному значенню ряду придається рівна вага в той час як в дійсності більший вплив на прогнозовані величини мають значення останніх років; припускається, що на протязі розглядаємого періоду часу параметри рівня тренду залишаються не змінними, в той час, як в багатьох випадках ці параметри змінюються з часом.

4. Використані джерела

1. Беседин В.Ф. Плановое управление экономикой// Научно-методические основы планирования и прогнозирование развития экономики. - К.: Наукова думка, 1986. - Т.4. - 328 с.

2. Бестужев-Лада И.В. Социальное прогнозирование: особенности и проблемы//Социальное прогнозирование. - М.: Мысль, 1975.- 236 с.

3. Вишнев СМ. Основы комплексного прогнозирования. - М.:Наука, 1977. - 287 с.

4. Геец В.М. Прогнозирование динамики и структуры общественного производства союзной республики. - К.: Наукова думка,1987. - 270 с.

5. Глівенко СВ., Соколов М.О., Теліженко О.. Економічне прогнозування: Навч. посіб. для студентів вузів. - Суми: ВПП Мрія-1ЛТД, 2000. - 120 с

6. Голанский М.М. Экономическое прогнозирование. - .: Наука,1983. - 170 с.

7. Гордон Менер. Стратегічне планування: Семінар для працівників державного сектору. - Джорджія: Університет, 1998.

8. Горелова В.Л., Мельникова Е.Н. Основы прогнозирования систем: Учеб. пособ. для вузов. - .: Высшая школа, 1986. - 287 с.

9. Данилов-Данильян В.И., Рыбкин А.А. Прогнозирование и планирование//Системные исследования: Методология. Проблемы: Ежегодник. - М.: Наука, 1981. - С. 39-59.

10. Емельянов А.С, Беседин В.Ф., Климченко Г.Д. Региональная экономика: Планирование, прогнозирование, управление. - К.:Наукова думка, 1989. - 272 с.

11. Емельянов А.С, Беседин В.Ф., Бондарь И.К. Прогнозирование показателей с помощью моделей. - К.: Наукова думка. 1984. —316 с.

12. Емельянов А.С. Эконометрия и прогнозирование. - М.: Экономика, 1985. - 208 с.

13. Заставный Ф.Д. Территориальные предплановые прогнозы. - К.:Наукова думка, 1988. - 184 с.

14. Ивахненко А.Г. Долгосрочное прогнозирование и управление сложными системами. - К.: Техника, 1975. - 372 с.

15. Калина А.В., Конева М.И., Ященко В.А. Современный экономический анализ и прогнозирование: Учеб.-метод, пособие. - К.: МАУП, 1997. - 272 с.

16. Комплексное региональное планирование и прогнозирование/АН СССР. Центр, экон.-мат. ин-т.; Под ред. Н.П.Федоренко,СО. Календжян. - М.: Наука, 1989. - 156 с.

17. Месхия Л.. Вопросы методологии регионального экономического прогнозирования. - М.: Наука, 1983. - 163 с.

18. Найман Эрик. Малая энциклопедия трейдера. - К.: Альфа Капитал; Логос, 1997. - 236 с.

19. Народнохозяйственное социальное экономическое планирование и прогнозирование/ К.А. Багрицкий, И.Н. Шокин, Р.Л. Раяц-кас; Отв. ред. Н.П. Федоренко, В.И. Денисов. - М.: Наука, 1989.- 240 с.

20. Основы экономического и социального прогнозирования: Учебник для вузов/Под, ред. В.Н. Мосина, Д.М. Крука. - .: Высшая школа, 1985. - 200 с.

21. Панасюк Б., Сергиенко И., Гуляницкий Л. Прогнозирование развития экономики Украины//Экономика Украины. - 1996. -№ 1. -С. 20-31.

22. Панасюк Б., Сменковский А. О некоторых методических подходах к краткосрочному прогнозированию макроэкономических показателей//Экономика Украины. - 1998. - №10. - С. 4-11.

23. Пашута М.Т., Калина А.В. Прогнозування та макроекономічне планування: Навч. посіб. - К.: МАУП, 1998. - 192 с.

24. Прогнозирование капиталистической экономики. Проблемы методологии. - М.: Мысль, 1970. — 448 с.

25. Рабочая книга по прогнозированию/ Редкол.: И.В. Бестужев-Ладаи др. - М.: Мысль, 1982. - 430 с.

26. Саркисян С.А, Голованов Л.В. Прогнозирование развития больших систем. - М.: Статистика, 1975. - 192 с.

27. Теория прогнозирования и принятия решений. — М.: Высшая школа, 1977. - 352 с.

28. Трисеев Ю.П. Долгосрочное прогнозирование экономических процессов (системные методы). - К.: Наукова думка, 1987. -130 с.

29. Цвиркун А.Д., Акинфиев В.К., Соловьев М.М. Моделирование развития крупномасштабных систем (на примере топливно-энергетических отраслей и комплексов). - М.: Экономика, 1983. -176 с.

30. Цыгичко В.Н. Прогнозирование социально-экономических процессов. - М.: Финансы и статистика, 1986. - 207 с.

31. Четыркин Е.М. Статистические методы прогнозирования. - М.: Статистика, 1977. - 184 с.

32. Хауштейн Г. Методы прогнозирования в социалистической экономике. - М.: Прогресс, 1971. - 300 с.

33. Эйерес Р. Научно-техническое прогнозирование и долгосрочное планирование. - М.: Мир, 1973. - 216 с.

34. Янч Э. Прогнозирование научно-технического прогресса. - М.: Прогресс, 1974. - 240 с.

Скачать архив с текстом документа