Производная в курсе алгебры средней школы

СОДЕРЖАНИЕ: Южно-Сахалинский Государственный Университет Кафедра математики Курсовая работа Тема: Производная в курсе алгебры средней школы Автор: Меркулов М. Ю.

Южно-Сахалинский Государственный Университет

Кафедра математики

Курсовая работа

Тема: Производная в курсе алгебры средней школы

Автор:	Меркулов М. Ю.
Группа:	411
Руководитель:	Чуванова Г. М.
Оценка:

Южно-Сахалинск

2002г
Введение

В первой главе курсовой работы речь пойдет о понятии производной, ее истории и областях ее применения. Во второй главе будет детально рассмотрен курс изучения производной трех учебников по алгебре и началам анализа для 10-11кл. : Алимова, Башмакова и под редакцией Колмогорова. Цель курсовой работы – раскрыть понятие производной, рассмотреть систему ее изучения в учебниках средней школы, охарактеризовать особенности изложения материала и дать рекомендации по поводу использования этих учебников.

Производная и ее применение

1. Понятие производной

1-1. Исторические сведения

Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:

1) о разыскании касательной к произвольной линии

2) о разыскании скорости при произвольном законе движения

Еще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500 - 1557 гг.) - здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.

В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.

1-2. Понятие производной

Пусть y = f(x) есть непрерывная функция аргумента x, определенная в промежутке (a; b), и пусть х₀ - произвольная точка этого промежутка

Дадим аргументу x приращение x, тогда функция y = f(x) получит приращение y = f(x + x) - f(x). Предел, к которому стремится отношение y / x при x 0, называется производной от функции f(x).

y(x)=

1-3. Правила дифференцирования и таблица производных

C = 0	(xⁿ ) = nx^n-1	(sin x) = cos x
x = 1	(1 / x) = -1 / x²	(cos x) = -sin x
(Cu)=Cu	(x) = 1 / 2x	(tg x) = 1 / cos² x
(uv) = uv + uv	(a^x ) = a^x ln x	(ctg x) = 1 / sin² x
(u / v)=(uv - uv) / v²	(e^x ) = e^x	(arcsin x) = 1 / (1- x² )
(log_a x) = (log_a e) / x	(arccos x) = -1 / (1- x² )
(ln x) = 1 / x	(arctg x) = 1 / (1+ x² )
(arcctg x) = -1 / (1+ x² )

2. Геометрический смысл производной

2-1. Касательная к кривой

Пусть имеем кривую и на ней фиксированную точку M и точку N. Касательной к точке M называется прямая, положение которой стремится занять хорда MN, если точку N неограниченно приближать по кривой к M.

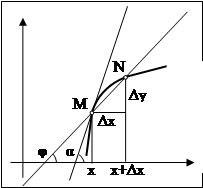Рассмотрим функцию f(x) и соответствующую этой функции кривую y = f(x). При некотором значении x функция имеет значение y = f(x). Этим значениям на кривой соответствует точка M(x₀ , y₀ ). Введем новый аргумент x₀ + x, его значению соответствует значение функции y₀ + y = f(x₀ + x). Соответствующая точка - N(x₀ + x, y₀ + y). Проведем секущую MN и обозначим угол, образованный секущей с положительным направлением оси Ox. Из рисунка видно, что y / x = tg . Если теперь x будет приближаться к 0, то точка N будет перемещаться вдоль кривой , секущая MN - поворачиваться вокруг точки M, а угол - меняться. Если при x 0 угол стремится к некоторому , то прямая, проходящая через M и составляющая с положительным направлением оси абсцисс угол , будет искомой касательной. При этом, ее угловой коэффициент:

То есть, значение производной f (x) при данном значении аргумента x равно тангенсу угла, образованного с положительным направлением оси Ox касательной к графику функции f(x) в точке M(x, f(x)).

Касательная к пространственной линии имеет определение, аналогичное определению касательной к плоской кривой. В этом случае, если функция задана уравнением z = f(x, y), угловые коэффициенты при осях OX и OY будут равны частным производным f по x и y.

2-2. Касательная плоскость к поверхности

Касательной плоскостью к поверхности в точке M называется плоскость, содержащая касательные ко всем пространственным кривым поверхности, проходящим через M - точку касания.

Возьмем поверхность, заданную уравнением F(x, y, z) = 0 и какую-либо обыкновенную точку M(x₀ , y₀ , z₀ ) на ней. Рассмотрим на поверхности некоторую кривую L, проходящую через M. Пусть кривая задана уравнениями

x = (t); y = (t); z = (t).

Подставим в уравнение поверхности эти выражения. Уравнение превратится в тождество, т. к. кривая целиком лежит на поверхности. Используя свойство инвариантности формы дифференциала, продифференцируем полученное уравнение по t:

Уравнения касательной к кривой L в точке M имеют вид:

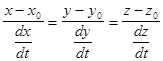
Т. к. разности x - x₀ , y - y₀ , z - z₀ пропорциональны соответствующим дифференциалам, то окончательное уравнение плоскости выглядит так:

F_x (x - x₀ ) + F_y (y - y₀ ) + F_z (z - z₀ )=0

и для частного случая z = f(x, y):

Z - z₀ = F_x (x - x₀ ) + F_y (y - y₀ )

Пример: Найти уравнение касательной плоскости в точке (2a; a; 1,5a) гиперболического параболоида

Решение :

Z_x = x / a = 2; Z_y = -y / a = -1

Уравнение искомой плоскости:

Z - 1.5a = 2(x - 2a) - (Y - a) или Z = 2x - y - 1.5a

3. Использование производной в физике

3-1. Скорость материальной точки

Пусть зависимость пути s от времени t в данном прямолинейном движении материальной точки выражается уравнением s = f(t) и t₀ -некоторый момент времени. Рассмотрим другой момент времени t, обозначим t = t - t₀ и вычислим приращение пути: s = f(t₀ + t) - f(t₀ ). Отношение s / t называют средней скоростью движения за время t, протекшее от исходного момента t₀ . Скоростью называют предел этого отношения при t 0.

Среднее ускорение неравномерного движения в интервале (t; t + t) - это величина a=v / t. Мгновенным ускорением материальной точки в момент времени t будет предел среднего ускорения:

То есть первая производная по времени (v(t)).

Пример: Зависимость пройденного телом пути от времени задается уравнением s = A + Bt + Ct² +Dt³ (C = 0,1 м/с, D = 0,03 м/с² ). Определить время после начала движения, через которое ускорение тела будет равно 2 м/с² .

Решение :

v(t) = s(t) = B + 2Ct + 3Dt² ; a(t) = v(t) = 2C + 6Dt = 0,2 + 0,18t = 2;

1,8 = 0,18t; t = 10 c

3-2. Теплоемкость вещества при данной температуре

Для повышения различных температур T на одно и то же значение, равное T₁ - T, на 1 кг. данного вещества необходимо разное количество теплоты Q₁ - Q, причем отношение

для данного вещества не является постоянным. Таким образом, для данного вещества количество теплоты Q есть нелинейная функция температуры T: Q = f(T). Тогда Q = f(t + T) - f(T). Отношение

называется средней теплоемкостью на отрезке [T; T + T], а предел этого выражения при T 0 называется теплоемкостью данного вещества при температуре T.

3-3. Мощность

Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:.

4. Дифференциальное исчисление в экономике

4-1. Исследование функций

Дифференциальное исчисление - широко применяемый для экономического анализа математический аппарат. Базовой задачей экономического анализа является изучение связей экономических величин, записанных в виде функций. В каком направлении изменится доход государства при увеличении налогов или при введении импортных пошлин? Увеличится или уменьшится выручка фирмы при повышении цены на ее продукцию? В какой пропорции дополнительное оборудование может заменить выбывающих работников? Для решения подобных задач должны быть построены функции связи входящих в них переменных, которые затем изучаются с помощью методов дифференциального исчисления. В экономике очень часто требуется найти наилучшее или оптимальное значение показателя: наивысшую производительность труда, максимальную прибыль, максимальный выпуск, минимальные издержки и т. д. Каждый показатель представляет собой функцию от одного или нескольких аргументов. Таким образом, нахождение оптимального значения показателя сводится к нахождению экстремума функции.

По теореме Ферма, если точка является экстремумом функции, то производная в ней либо не существует, либо равна 0. Тип экстремума можно определить по одному из достаточных условий экстремума:

1) Пусть функция f(x) дифференцируема в некоторой окрестности точки x₀ . Если производная f (x) при переходе через точку x₀ меняет знак с + на -, то x₀ - точка максимума, если с - на +, то x₀ - точка минимума, если не меняет знак, то в этой точке нет экстремума.

2) Пусть функция f(x) дважды дифференцируема в некоторой окрестности точки x₀ , причем f (x₀ ) = 0, f (x₀ ) 0, то в точке x₀ функция f(x₀ ) имеет максимум, если f (x₀ ) 0 и минимум, если f (x₀ ) 0.

Кроме того, вторая производная характеризует выпуклость функции (график функции называется выпуклым вверх [вниз] на интервале (a, b), если он на этом интервале расположен не выше [не ниже] любой своей касательной).

Пример: выбрать оптимальный объем производства фирмой, функция прибыли которой может быть смоделирована зависимостью:

(q) = R(q) - C(q) = q² - 8q + 10

Решение:

(q) = R(q) - C(q) = 2q - 8 = 0 q_extr = 4

При q q_extr = 4 (q) 0 и прибыль убывает

При q q_extr = 4 (q) 0 и прибыль возрастает

При q = 4 прибыль принимает минимальное значение.

Каким же будет оптимальный объем выпуска для фирмы? Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (p(q = 8) = p(q = 0) = 10), то оптимальным решением будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и / или оборудования. Если же фирма способна производить больше 8 единиц, то оптимальным для фирмы будет выпуск на пределе своих производственных мощностей.

4-2. Эластичность спроса

Эластичностью функции f(x) в точке x₀ называют предел

Спрос - это количество товара, востребованное покупателем. Ценовая эластичность спроса E_D - это величина, характеризующая то, как спрос реагирует на изменение цены. Если E_D 1, то спрос называется эластичным, если E_D 1, то неэластичным. В случае E_D =0 спрос называется совершенно неэластичным, т. е. изменение цены не приводит ни к какому изменению спроса. Напротив, если самое малое снижение цены побуждает покупателя увеличить покупки от 0 до предела своих возможностей, говорят, что спрос является совершенно эластичным. В зависимости от текущей эластичности спроса, предприниматель принимает решения о снижении или повышении цен на продукцию.

4-3. Предельный анализ

Важный раздел методов дифференциального исчисления, используемых в экономике - методы предельного анализа, т. е. совокупность приемов исследования изменяющихся величин затрат или результатов при изменениях объемов производства, потребления и т. п. на основе анализа их предельных значений. Предельный показатель (показатели) функции - это ее производная (в случае функции одной переменной) или частные производные (в случае функции нескольких переменных)

В экономике часто используются средние величины: средняя производительность труда, средние издержки, средний доход, средняя прибыль и т. д. Но часто требуется узнать, на какую величину вырастет результат, если будут увеличены затраты или наоборот, насколько уменьшится результат, если затраты сократятся. С помощью средних величин ответ на этот вопрос получить невозможно. В подобных задачах требуется определить предел отношения приростов результата и затрат, т. е. найти предельный эффект. Следовательно, для их решения необходимо применение методов дифференциального исчисление.

5. Производная в приближенных вычислениях

5-1. Интерполяция

Интерполяцией называется приближенное вычисление значений функции по нескольким данным ее значениям. Интерполяция широко используется в картографии, геологии, экономике и других науках. Самым простым вариантом интерполяции является форма Лагранжа, но когда узловых точек много и интервалы между ними велики, либо требуется получить функцию, кривизна которой минимальна то прибегают к сплайн-интерполяции, дающей бльшую точность.

Пусть K_n - система узловых точек a = x₀ x₁ … x_n = b. Функция S_k (x) называется сплайн-функцией S_k (x) степени k0 на K_n , если

а) S_k (x) є C^k ^-1 ([a, b])

б) S_k (x) - многочлен степени не большей k

Сплайн-функция _k (x) є S_k (K_n ) называется интерполирующей сплайн-функцией, если _k (x_j ) = f(x_j ) для j = 0,1,…,n

В приложениях часто бывает достаточно выбрать k=3 и применить т. н. кубическую интерполяцию.

Т. к. s(x) на каждом частичном интервале есть многочлен третьей степени, то для x є [x_j _-1 ,x_j ]

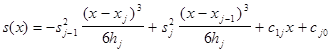
Здесь s² _j , c_j ₁ , c_j ₀ неизвестны для j = 1, 2, …, n

Последние исключаются в силу требования s(x_j ) = y_j :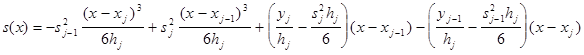Дифференцируя эту функцию и учитывая, что s(x) на всем интервале и, следовательно, в частности, в узлах должна быть непрерывна, окончательно получаем систему уравнений:

относительно n+1 неизвестных s² ₀ , s² ₁ ,…, s² _n. Для однозначного их определения в зависимости от задачи добавляются еще два уравнения:

Нормальный случай( N):

Периодический случай( P) (т. е. f( x+( x_n - x₀ ))= f( x)):

Заданное сглаживание на границах:

Пример: сплайн-интерполяция функции f(x)=sinx, n=4.

Функция периодическая, поэтому используем случай P.

j	x_j	y_j	h_j	y_j -y_j-1
0	0	0	/2	1
1	/2	1	/2	-1
2		0	/2	-1
3	3/2	-1	/2	1
4	2	0

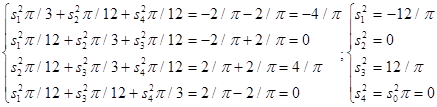
Сплайн-функция получается такая:

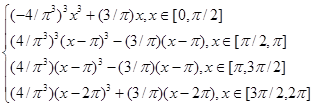
5-2. Формула Тейлора

Разложение функций в бесконечные ряды позволяет получить значение функции в данной точке с любой точностью. Этот прием широко используется в программировании и других дисциплинах

Говорят, что функция разлагается на данном промежутке в степенной ряд, если существует такой степенной ряд a₀ + a₁ (x - a) + a₂ (x - a)² + … + a_n (x - a)ⁿ + …, который на этом промежутке сходится к данной функции. Можно доказать, что это разложение единственно:

Пусть функция f(x) бесконечно дифференцируема в точке a. Степенной ряд вида

называется рядом Тейлора для функции f(x), записанным по степеням разности (x - a). Вообще, чтобы ряд Тейлора сходился к f(x) необходимо и достаточно, чтобы остаточный член ряда стремился к 0. При a = 0 ряд Тейлора обычно называют рядом Маклорена.

С помощью ряда Маклорена можно получить простые разложения элементарных функций:

5-3. Приближенные вычисления

Часто бывает, что функцию f(x) и ее производную легко вычислить при x = a, а для значений x, близких к a, непосредственное вычисление функции затруднительно. Тогда пользуются приближенной формулой, полученной с помощью формулы Тейлора:

Пример: Извлечь квадратный корень из 3654

Решение: , x₀ =3654. Легко вычисляются значения f(x) и при x = 3600. Формула при a = 3600, b=54 дает:

С помощью этой формулы можно получить несколько удобных формул для приближенных вычислений:

Производная в школьном курсе алгебры

1. Структура учебников

Колмогоров:

§4. Производная

12. Приращение функции

13. Понятие о производной

14. Понятия о непрерывности и предельном переходе

15. Правила вычисления производных

16. Производная сложной функции

17. Производные тригонометрических функций

§5. Применение непрерывности и производной

18. Применения непрерывности

19. Касательная к графику функции

20. Приближенные вычисления

21. Приоизводная в физике и технике

§6. Применение производной к исследованию функций

22. Признак возрастания (убывания) функции

23. Критические точки функции, максимумы и минимумы

24. Примеры применения производной к исследованию функции

25. Наибольшее и наименьшее значения функции

Алимов:

Глава V. Производная и ее применение

§22. Производная

§23. Производная степенной функции

§24. Правила дифференцирования

§25. Производные некоторых элементарных функций

§26. Геометрический смысл производной

Глава VI. Применение производной к исследованию функций

§27. Возрастание и убывание функции

§28. Экстремумы функции

§29. Применение производной к построению графиков функции

§30. Наибольшее и наименьшее значения функции

Башмаков:

Глава II. Производная и ее применение

Вводная беседа

Механический смысл производной

Геометрический смысл производной

Определение производной

Предельные переходы

§1. Вычисление производной

Схема вычисления производной

Правила дифференцирования

Производная степени

Линейная замена аргумента

§2. Исследование функций с помощью производной

Связь свойств функции и ее производной

Особые точки

Решение задач

Построение графика функции

§3. Приложения производной

Скорость и ускорение

Скорость криволинейного движения

Дифференциал

Дифференциал в физике

Задачи на максимум и минимум

Приближенные формулы

2. Понятие производной

2-1. Определение производной

В учебниках Алимова и Башмакова вначале определение производной дается через механический смысл: производная – это мгновенная скорость. Это соответствие, пожалуй, наиболее доступно для понимания школьника.

Рассмотрев задачу на скорость, Алимов сразу же переходит к точному определению производной через пределы, кратко объяснив значение понятия «предел» в той же задаче применительно к мгновенной скорости.

Башмаков же последовательно и детально рассматривает механический и геометрический смысл, рассматривая производную на разных случаях, и только потом переходит к точному определению.

Подход Колмогорова отличается тем, что глава, посвященная производной, начинается с пункта, в котором дается определение приращения функции. Понятие приращения рассматривается на примерах. Третий пример показывает, как найти угловой коэффициент секущей через приращение. В следующем пункте автор объясняет, что такое касательная к графику функции и дает определение мгновенной скорости. Причем, определение предела не рассматривается, вместо этого Колмогоров пользуется понятием «стремится к».

Проанализировав систему ознакомления учащегося с понятием производной в этих учебниках, можно выявить следующие особенности: короткое вступление главы о производных в учебнике Алимова дает возможность учащимся, получив минимум информации о производной, как можно быстрее приступить к вычислению производных. Далее, понятие производной обогащается новыми приложениями и свойствами и все это немедленно подкрепляется задачами. Колмогоров и Башмаков стремятся вначале подвести достаточно большую базу примеров и соответствий, опираясь на более легкие по усвояемости понятия и затем приступить к вычислениям.

2-2. Геометрический смысл производной

У Колмогорова и Башмакова понятие касательной к графику функции начинается с аналогии. Важно установить связь у учеников между абстрактным понятием касательной и уже освоенными геометрическими объектами, интуитивные образы которых уже сформированы в сознании. Так, увеличивая масштаб графика функции, авторы обращают внимание школьников на то, что график все больше становится похож на прямую. Также они замечают, что, проводя отрезки между точками графика, мы можем получить его приближенное изображение. Все это позволяет представить себе «устройство» кривых. Используется наглядная иллюстрация «вырезания» графика из бумаги – касательной в данной точке будет являться положение ножниц, когда разрез дойдет до этой точки.

В учебнике Алимова пункт “геометрический смысл производной” расположен в самом конце, после объяснения методов вычисления. Алимов аналогиями пренебрегает, зато дает конкретное определение геометрического смысла производной: значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке.

Определение касательной и вывод ее формулы дается через рассмотрение хорд (см. гл. 1 п.2-1). Используются приращения и пределы.

2-3. Непрерывность функции и предельный переход

Колмогоров дает определение понятия непрерывности функции: если f (x)f (x₀ ) при xx₀ , то функцию f (x) называют непрерывной. Вообще, в этом пункте автор очень углубляется в математический анализ и довольно скрупулезно разбирает свойство непрерывности и предельный переход. У Башмакова предельный переход объясняется на примерах, не вдаваясь в подробности.

3. Вычисление производной

3-1. Правила дифференцирования

Напомним основные правила дифференцирования:

сумма: (u + v)’ = u’ + v’

коэффициент: (Cu)’ = Cu’

произведение: (uv)’ = u’v + uv’

частное: (u / v)=(uv - uv) / v²

В учебниках Башмакова и Колмогорова все эти формулы выводятся, каждый шаг объясняется. Учебник Алимова содержит доказательства только двух первых формул, зато к каждой формуле есть по 1-2 примера.

В учебнике Колмогорова рассматривается формула производной сложной функции (гл 2, §16):

f(g(x))’ = f ’(g(x))g’(x)

Вначале автор дает определение сложной функции, затем выводит формулу и приводит несколько примеров нахождения производной сложных функций. Алимов решил упростить данный раздел, заменив формулу сложной функции на ее частный случай – линейную замену аргумента:

(f(kx + b))’ = kf ‘(kx + b)

Эта формула, конечно, гораздо менее емкая, зато ее доказательство короче и менее абстрактно. Башмаков же включил в учебник обе формулы.

3-2. Производные элементарных функций

Проблема заключается в том, что если тема «производные» дается перед рассмотрением каких-либо элементарных функций, то производные этих функций придется рассматривать позже, что может отвлечь от сути. С другой стороны, помещая производные в самый конец учебника, сложность материала может повышаться неравномерно, что может сказаться на успеваемости.

Башмаков посвящает вычислению производной через приращения целый пункт, где выводит 5 формул (для линейной функции, квадрата, куба, гиперболической функции, корня). С этого пункта и начинается собственно вычисление производных. Далее, после рассмотрения правил дифференцирования, выводится формула производной степени. Производные показательной и логарифмической функций рассматривается в соответствующей главе, а производные тригонометрических функций вовсе исключены из курса.

В учебнике Колмогорова формулы производных показательной и логарифмической функций также выводятся и применяются в решении задач позже. Однако, производные тригонометрических функций, уже изученных к этому моменту, даются в главе «производная» в виде отдельного пункта. Кстати говоря, в ходе вывода формулы производной синуса, доказывается следующее утверждение:

lim (sin (x) / x) = 1

Доказательство усложнено тем, что переменная выступает как угол и длина, необходим переход от длины дуги к длине отрезка. Он обосновывается довольно расплывчато, но объяснения интуитивно вполне понятны. Имея в распоряжении формулу производной синуса, нетрудно найти производные остальных функций.

Алимов рассматривает степенную функцию перед правилами дифференцирования, а формулы производных других элементарных функций (показательной, логарифмической, тригонометрических) – после и в отдельном пункте. Доказательство приводится только для синуса, но для каждой функции есть решенная задача. Удобство заключается в том, что все элементарные функции и правила дифференцирования рассматриваются последовательно и нет необходимости возвращаться к уже пройденному материалу.

4. Исследование функций

4-1. Возрастание и убывание функций

В начале раздела о исследовании функций в учебнике Башмакова приводятся две теоремы: о том, что функция имеющая на промежутке производную, тождественно равную 0, постоянна на этом промежутке и признак монотонности функции. Затем идет формулировка признаков возрастания / убывания функции – они находятся в начале разделов учебников Алимова и Колмогорова. Колмогоров доказывает эти признаки на основе формулы Лагранжа:

Алимов доказательство не приводит. Затем идут примеры, наглядно показывающие, как находить промежутки возрастания / убывания.

4-2. Экстремумы функций

Основополагающими теоремами в этом пункте являются: необходимое условие экстремума (производная в точке экстремума должна быть равна 0), признаки максимума / минимума функции. Согласно просматривающемуся стилю авторов, Колмогоров методично доказывает каждую теорему, Алимов делает упор на рассмотрение задач, а Башмаков по возможности в доказательствах и рассуждениях обходится без формул, предпочитая рассказ о свойствах производной.

Замечу, что Башмаков выделил пункт для рассмотрения т. н. особых точек. Это точки, в которых производная не существует, но функция может быть непрерывной. Колмогоров рассматривает их в пункте «применение непрерывности» . Кроме того, там же рассматривается важнейший метод исследования поведения функции – метод интервалов.

4-3. Схема исследования функций

Колмогоров:

1) Нахождение области определения

2) Проверка на четность / нечетность

3) Нахождение точек пересечения с осями

4) Нахождение промежутков знакопостоянства

5) Нахождение промежутков возрастания и убывания

6) Нахождение точек экстремума и значений функции в этих точках

7) Исследование поведения функции в окрестностях «особых» точек и бесконечности

Башмаков и Алимов исследуют функцию только на монотонность.

5. Приложения производной

5-1. Применение производной в физике

Ранее уже был рассмотрен механический смысл производной – как найти скорость (ускорение – производная от скорости – вторая производная функции). Учебник Башмакова показывает, как производная используется также при нахождении таких физических характеристик, как сила, импульс, кинетическая энергия. Разъясняется суть понятия дифференциала: дифференциалом функции называют произведение производной на приращение аргумента. Рассказывается, как с помощью дифференциала можно найти заряд, работу, массу тонкого стержня, теплоту.

Колмогоров также приводит примеры использования производной в физике: нахождение мощности, линейной плотности. Также он объясняет с помощью производной принцип действия параболических телескопов.

5-2. Приближенные вычисления

Формула для приближенных вычислений разбирается в учебнике Колмогорова и Башмакова. Авторы указывают на сходство графиков функции и касательной и значения будут ненамного различаться при достаточно малом приращении. Эта тема носит практический характер. Рассмотрены несколько примеров.

Заключение

Принимая в расчет вышеизложенное, я могу дать такую характеристику этим учебникам:

Учебник под редакцией Колмогорова характеризуется большим объемом материала по производной и высокой степенью детальности. Как следствие – высокий уровень подготовки и некоторая сложность в понимании. Этот учебник по праву наиболее часто используется в обычных школах.

Учебник Алимова делает больший упор на практическую сторону. В тексте много примеров решения задач, некоторые пункты даже целиком состоят из них. К каждому пункту прилагается большой набор задач для самостоятельного решения. Доказательства – слабая сторона учебника, т. к. они кратки, а зачастую их нет совсем. Некоторые аспекты темы опущены.

В учебнике Башмакова материал излагается крайне сжато, но последовательно и доказательства более просты и понятны. Все абстрактные математические понятия находят свои житейские прототипы и рассматриваются на конкретных примерах. Учебник больше подходит для самостоятельного изучения материала.

Литература

М. Я. Выгодский	Справочник по высшей математике
И. Н. Бронштейн, К. А. Семендяев	Справочник по математике для инженеров и учащихся ВТУЗов
И. М. Уваренков, М. З. Маллер	Курс математического анализа,т.1
В. А. Дударенко, А.А. Дадаян	Математический анализ
Н. С. Пискунов	Дифференциальное и интегральное исчисления
Т. И. Трофимова	Курс физики
О. О. Замков А. В. Толстопятенко Ю. Н. Черемных	Математические методы в экономике
А. С. Солодовников В. А. Бабайцев А. В. Браилов И. Г. Шандра	Математика в экономике
Под редакцией А.М Колмогорова	Алгебра и начала анализа
Ш. А. Алимов Ю. М. Колягин Ю. В. Сидоров Н. Е. Федорова М. И. Шабунин	== ==
М. И. Башмаков	== ==

Содержание:

Введение

Глава 1. Производная и ее применение

1. Понятие производной

1-1. Исторические сведения

1-2. Понятие производной

1-3. Правила дифференцирования и таблица производных

2. Геометрический смысл производной

2-1. Касательная к кривой

2-2. Касательная плоскость к поверхности

3. Использование производной в физике

3-1. Скорость материальной точки

3-2. Теплоемкость при данной температуре

3-3. Мощность

4. Дифференциальное исчисление в экономике

4-1. Исследование функций

4-2. Эластичность спроса

4-3. Предельный анализ

5. Производная в приближенных вычислениях

5-1. Интерполяция

5-2. Формула Тейлора

5-3. Приближенные вычисления

Глава 2. Производная в школьном курсе алгебры

1. Структура учебников

2. Понятие производной

2-1. Определение производной

2-2. Геометрический смысл производной