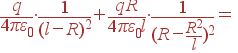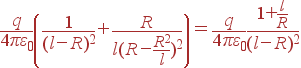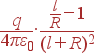Проводники в электрическом поле. Электростатический метод изображений
СОДЕРЖАНИЕ: Проводники в электрическом поле. Электростатический метод изображений. М.И. Векслер, Г.Г. Зегря Поле внутри проводника равно нулю, поэтому проводники геометрически ограничивают область, где должны решаться уравнения электростатики. На поверхности проводника = const (эквипотенциальность).
Проводники в электрическом поле. Электростатический метод изображений.
М.И. Векслер, Г.Г. Зегря
Поле внутри проводника равно нулю, поэтому проводники геометрически ограничивают область, где должны решаться уравнения электростатики. На поверхности проводника = const (эквипотенциальность). Это достигается индуцированием зависящей от координаты поверхностной плотности заряда . Поле ортогонально к поверхности проводника, но не обязательно однородно. Заряд на поверхности связан с полем как = 0E.
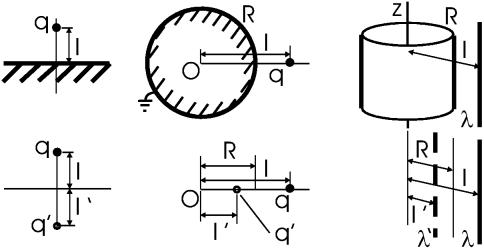
Метод изображений состоит в замене системы заряды + проводящая поверхность на систему заряды + изображения. Правила построения изображений обеспечивают эквипотенциальность требуемой поверхности. Для точечного заряда q, расположенного на расстоянии l от плоскости или центра сферы, а также для прямой нити , расположенной на расстоянии l от оси цилиндра:
|
|
![]() плоскость q q = –q, l l = l
плоскость q q = –q, l l = l
заземленная сфера q q = –qR/l, l l = R2/l
цилиндр –, l l = R2/l
Если сфера не заземлена, то надо еще дополнительно поставить заряд +qR/l в начало координат. Цилиндр и плоскость заземлены по определению (они простираются до бесконечности, где = 0).
Основным практическим случаем является проводящая плоскость: например Земля. Он легко обобщается на систему зарядов (нитей, колец и т. д.) - всю ее надо отобразить относительно плоскости.
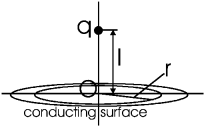
Задача. Точечный заряд q находится на расстоянии l от проводящей плоскости. Найти плотность индуцированного заряда как функцию расстояния r от проекции заряда на плоскость.
Ответ: ![]()
|
|
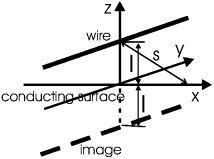
Задача. Бесконечная прямая нить, несущая заряд на единицу длины, висит над проводящей плоскостью на расстоянии l от нее. Найти распределение электрического поля и поверхностной плотности индуцированного заряда вблизи плоскости.
Решение: Сначала находим поле одной нити по теореме Гаусса, затем отображаем нить и ищем поле от нити-изображения –, далее векторно суммируем эти поля. После этого можно найти в любой точке как –0· Ewire+image.
Поле одной нити на расстоянии s от нее равно
|
|
и направлено от оси нити или к ней. Поэтому поле одной нити в плоскости на расстоянии x от проекции нити на плоскость будет (![]() ):
):
|
|
Такое же по абсолютной величине поле создается нитью-изображением. При векторном суммировании полей двух нитей параллельные плоскости компоненты уничтожаются, а перпендикулярные ей - удваиваются:
|
|
Соответственно, имеем плотность индуцированного заряда:
|
|
Проинтегрировав (x) по x от – до +, можно убедиться, что суммарный индуцированный заряд на единицу длины проекции нити составляет –, как и должно быть.
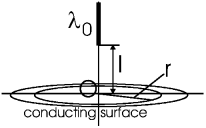
Задача. Очень длинная равномерно заряженная зарядом 0 нить расположена по оси z и не доходит до проводящей плоскости xy на расстояние l. Найти поле вблизи плоскости xy как функцию расстояния r от начала координат.
Ответ: ![]()
|
|
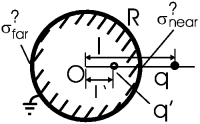
Задача. На расстоянии l от центра заземленной сферы радиуса Rl расположен точечный заряд q. Найти плотность заряда, индуцированного в ближайшей к заряду и в наиболее удаленной от него точках шара.
Решение: По правилам размещения заряда-изображения, помещаем заряд –qR/l в точку на оси центр сферы - заряд q, удаленную от центра на расстояние R2/l. Тогда расстояние от заряда-изображения до ближайшей к заряду точки сферы будет R–R2/l. В этой точке и поле от истинного заряда, и поле от заряда-изображения направлены к центру сферы, а их сумма по абсолютной величине будет
| Enear |
= |
|
|
| = |
|
Сразу же находится :
|
|
Аналогично находим плотность индуцированного заряда в удаленной точке, только там поле от заряда q направлено от центра, а от изображения - на центр. Сумма этих полей оказывается направленной к центру и по модулю равной:
| Efar |
= |
|
так что
|
|
Список литературы
1. И.Е. Иродов, Задачи по общей физике, 3-е изд., М.: Издательство БИНОМ, 1998. - 448 с.; или 2-е изд., М.: Наука, 1988. - 416 с.
2. В.В. Батыгин, И.Н. Топтыгин, Сборник задач по электродинамике (под ред. М.М. Бредова), 2-е изд., М.: Наука, 1970. - 503 с.
3. Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика. т.8 Электродинамика сплошных сред, 2-е изд., М.: Наука, 1992. - 661 с.