Работа с двумерными числовыми массивами
СОДЕРЖАНИЕ: Анализ методики использования многомерных массивов в среде Delphi. Общее понятие массивов, их реализация, достоинства, недостатки. Массивы в Object Pascal. Описание функциональной структуры приложения: модуль MatrixOperations, модуль fileIO, модуль form.Содержание
Введение
1. Теоретическая часть
1.1 Общее понятие о массивах
1.1.1 Определение и область применения
1.1.2 Специфические типы массивов
1.1.3 Реализация массивов
1.1.4 Достоинства массивов
1.1.5 Недостатки массивов
1.2 Массивы в Object Pascal
1.2.1 Статические массивы
1.2.2 Динамические массивы
1.2.3 Функции для работы с массивами
1.3 Использование массивов в рамках проекта
2. Практическая часть
2.1 Постановка задачи
2.2 Функциональная структура приложения
2.3 Описание модулей
2.3.1 Модуль MatrixOperations
2.3.2 Модуль fileIO
2.4 Модуль form
3. Эксплуатационная документация
3.1 Описание применения
3.2 Руководство оператора
Выводы
Приложения
Введение
В вычислительной технике данные обычно отличают от программ. Программа является набором инструкций, которые детализируют вычисление или задачу, производимую компьютером. Данными же традиционно называется всё, что не выступает в роли программы. В языках высокого уровня данные воплощаются в виде переменных.
Часто перед программистами встают задачи, связанные с обработкой стразу множества значений данных. В таких случаях крайне неудобно для хранения каждого значения заводить отдельную именованную переменную. Для такой ситуации синтаксис многих языков предусматривает создание массивов – множеств переменных, доступ к которым осуществляется посредством одного имени (имени массива) и одного или нескольких индексов.
Данная курсовая работа рассматривает методики использования многомерных массивов в среде Delphi. Она демонстрирует использование встроенных возможностей языка, а так же применение широко известных операций над массивами, таких как последовательный обход значений, сортировка, циклический сдвиг.
1. Теоретическая часть
1.1 Общее понятие о массивах
1.1.1 Определение и область применения
Массив (или индексный массив), это именованный набор однотипных переменных, расположенных в памяти непосредственно друг за другом, доступ к которым осуществляется по индексу. Количество используемых индексов массива может быть различным. Массивы с одним индексом называют одномерными, с двумя — двумерными и т. д. Одномерный массив нестрого соответствует вектору в математике, двумерный — матрице. Массивы хорошо подходят для отображения таких объектов реального мира, как строки (массивы символов), наборы координат, таблицы данных, математические множества и вообще множества однотипных объектов.
Без использования массивов не обойтись в таких областях программирования как работа с базами данных, компьютерная графика, визуализация результатов научных экспериментов, статистический анализ. Массивы являются входными и выходными параметрами процедур сортировки.
Поддержка индексных массивов (свой синтаксис объявления, функции для работы с элементами и т. д.) есть в большинстве высокоуровневых языков программирования. Максимально допустимая размерность массива, типы и диапазоны значений индексов, ограничения на типы элементов определяются языком программирования и/или конкретным транслятором.
В языках программирования, допускающих объявления программистом собственных типов, как правило, существует возможность создания типа «массив». В определении такого типа может указываться размер, тип элемента, диапазон значений и типы индексов. В дальнейшем возможно определение переменных созданного типа. Все такие переменные-массивы имеют одну структуру. Некоторые языки поддерживают для переменных-массивов операции присваивания (когда одной операцией всем элементам массива присваиваются значения соответствующих элементов другого массива).
1.1.2 Специфические типы массивов
Динамическим называется массив, размер которого может меняться во время исполнения программы. Для изменения размера динамического массива язык программирования, поддерживающий такие массивы, должен предоставлять встроенную функцию или оператор. Динамические массивы дают возможность более гибкой работы с данными, так как позволяют не прогнозировать хранимые объёмы данных, а регулировать размер массива в соответствии с реально необходимыми объёмами. Обычные, не динамические массивы называют ещё статическими .
Гетерогенным называется массив, в разные элементы которого могут быть непосредственно записаны значения, относящиеся к различным типам данных. Массив, хранящий указатели на значения различных типов, не является гетерогенным, так как собственно хранящиеся в массиве данные относятся к единственному типу — типу «указатель». Гетерогенные массивы удобны как универсальная структура для хранения наборов данных произвольных типов. Отсутствие их поддержки в языке программирования приводит к необходимости реализации более сложных схем хранения данных. С другой стороны, реализация гетерогенности требует усложнения механизма поддержки массивов в трансляторе языка.
Многомерные массивы, как правило, реализованные как одномерные массивы, каждый элемент которых является ссылкой на другой одномерный массив.
1.1.3 Реализация массивов
Стандартным способом реализации статических массивов с одним типом элементов является следующий:
Под массив выделяется непрерывный блок памяти объёмом
S*m1 *m2 *m3 …mn ,
где S — размер одного элемента, а m1 …mn — размеры диапазонов индексов (то есть количество значений, которые может принимать соответствующий индекс).
При обращении к элементу массива A[i1 , i2 , i3 , … in ] адрес соответствующего элемента вычисляется как
B+S*(i1p *m1 +i2p *m2 +…+i(n-1)p *mn-1 +inp ),
где B — база (адрес начала блока памяти массива), ikp -значение k-го индекса, приведённое к целому с нулевым начальным смещением.
Таким образом, адрес элемента с заданным набором индексов вычисляется так, что время доступа ко всем элементам массива одинаково. Первый элемент массива, в зависимости от языка программирования, может иметь различный индекс. Различают три основных разновидности массивов: с отсчетом от нуля (zero-based), с отсчетом от единицы (one-based) и с отсчетом от специфического значения заданного программистом (n-based).
Отсчет индекса элемента массивов с нуля более характерен для низкоуровневых языков программирования, однако этот метод был популяризирован в языках более высокого уровня языком программирования С.
Более сложные типы массивов — динамические и гетерогенные — реализуются сложнее.
1.1.4 Достоинства массивов
· Быстрый доступ к элементам, причём время доступа не зависит от длины массива
· Элементы расположены в памяти непосредственно друг за другом, что облегчает копирование и перемещение всего массива целиком
· Отсутствие необходимости в дополнительной памяти
1.1.5 Недостатки массивов
· для статического массива — отсутствие динамики, невозможность удаления или добавления элемента без сдвига других
· для динамического и/или гетерогенного массива — более низкое (по сравнению со статическим) быстродействие и дополнительные накладные расходы на поддержку динамических свойств и/или гетерогенности.
· при работе с массивом в отсутствие дополнительных средств контроля — угроза выхода за границы массива и повреждения «чужих» данных
1.2 Массивы в Object Pascal
Ключевое слово Array используется для определения одномерных и многомерные массивов данных. В Object Pascal существует два типа массивов
1.2.1 Статические массивы
Создаются с заранее определёнными, неизменяемыми размерами. Могут быть одномерными, или многомерными – во втором случае представляя из себя массив массивов (массивов массивов и так далее).
Величина каждой размерности определяется двумя способами, которые могут свободно сочетаться при определении многомерного массива:
· Тип Index , где Index – целый тип, обычно Byte или Word. Диапазон типа определяет диапазон размерности, например 0..255 для Byte
· Ordinal ..Ordinal . Таким образом, можно непосредственно задать диапазон размерности, например 12..44.
· Например:
1 var
2 wordArray : Array[Word] of Integer; // размер равен High(Word)
3 multiArray : Array[Byte, 1..5] of char; // двумерный массив
4 rangeArray : Array[5..20] of string; // размер равен 16
1.2.2 Динамические массивы
У для динамических массивов память заранее не выделяется, создаётся только указатель. У таких массивов необходимо задавать размер перед использованием. Например
SetLength (dynArray, 5);
устанавливает длину первой размерности массива dynArray в пять, при этом выделяется необходимая память. Для всех динамических массивов минимальный индекс равен нулю.
Отдельные подмассивы многомерного динамического массива могут иметь разные размеры, так как по сути они являются отдельными массивами.
Пример определения динамических массивов:
1 var
2 byteArray: Array of Byte; // одномерный массив
3 multiArray: Array of Array of string; // двумерный массив
1.2.3 Функции для работы с массивами
Copy (Source : array; StartIndex, Count : Integer ) : array – создает копию части массива.
High (type or variable): Ordinal type - возвращает верхнюю границу диапазона значений массива.
Length (const SourceArray: array): Integer - возвращает число элементов в массиве.
Low (type or variable): Ordinal type - возвращает нижнюю границу диапазона значений массива
SetLength (var ArrayToChange: Array type; Dim1Length: Integer {;Dim2Length: Integer; ...}) - изменяет размер динамического массива. Для многомерных массивов может принимать более одного параметра длины.
Slice (SourceArray: array; Count: Integer): array - создает часть массива для передачи его как параметр в процедуру или функцию.
При использовании динамических массивов необходимо помнить, что вызовы SetLength выделяют для массива дополнительную память, которую необходимо освобождать после окончания работы с массивом. Для этого ему нужно присвоить специальное значение nil .
1.3 Использование массивов в рамках данного проекта
Работа со статическими массивами более проста и менее затратна в плане использования ресурсов компьютера, но так как в задании нигде не оговариваются конкретные размеры исходных матриц, то было принято решение построить программу ну основе использования динамических массивов.
Приложение построено таким образом, что размер используемой матрицы можно менять во время выполнения, так же он автоматически определяется при загрузке исходных данных из файла. Размеры динамических массивов внутри программы изменяются соответствующим образом автоматически.
2. Практическая часть
2.1 Постановка задачи
Приложение предназначено для выполнения специфической обработки матриц. Исходные матрицы должны загружаться из файла, либо вводиться непосредственно в элементы интерфейса приложения.
Граничные условия на вводимые данные таковы:
· Размеры матрицы должны лежать в пределах [1; 2147483647]. Если введено число, выходящее из этого диапазона, либо значение, не являющееся целым числом, то размер устанавливается равным единице.
· Элементы матрицы должны лежать в пределах [-2147483648; 2147483647]. Если какой-то из элементов лежит вне этого диапазона, либо введёно значение, не являющееся целым числом, то элемент устанавливается равным нулю.
· В заданиях, связанных с подсчётом сумм элементов, результат может лежать в пределах [-9223372036854775808; 9223372036854775807]. Если сумма выходит за эти пределы, результат не определён.
2.2 Функциональная структура программы
Программа разделена на три модуля:
MatrixOperations – различные операции с матрицей
fileIO – сохранение матрицы в файл/ чтение матрицы из файла
form – форма приложения, процедуры обмена данными между массивами и элементами формы. Структура связей модулей такова:

2.3 Описание модулей
2.3.1 Модуль MatrixOperations
Это основной модуль программы, содержащий процедуры для выполнения матричных операций, предусмотренных заданием.
Определяет повсеместно используемые типы «матрица» и «вектор»:
1 type
2 TVector = array of integer;
3 TMatrix = array of TVector;
Поиск максимальных элементов в матрице.
Процедура GetMaxVals , которая, перебирая все строки матрицы, находит в каждой максимальный элемент, записывает его значение в массив maxVal, а его номер столбца в массив maxValCol. Предварительно процедура выделяет необходимую намять для этих массивов. Листинг:
1 {
2 формирует массив максимальных элементов maxVal и массив номеров столбцов,
3 содержащих максимальные элементы maxValCol на основе матрицы arr
4 }
5 procedure GetMaxVals(var maxVal, maxValCol: TVector; const arr: TMatrix);
6 var
7 RowN, ColN, maxInRow: integer;
8 begin
9 //выделим необходимый для каждого массива объём памяти
10 SetLength(maxVal, high(arr)+1);
11 SetLength(maxValCol, high(arr)+1);
12 for RowN:= low(arr) to high(arr) do
13 begin//для каждой строки
14 maxVal[RowN]:= low(integer);//по умолчанию максимальное значение -2147483648
15 maxValCol[RowN]:= -1;//по умолчанию номер столбца с макс элементом -1
16 for ColN:= low(arr[RowN]) to high(arr[RowN]) do
17 begin//для каждого столбца
18 if arr[RowN, ColN] maxVal[RowN] then
19 begin//если элемент больше макс значения, то
20 maxVal[RowN]:= arr[RowN, ColN];//максимальное значение приравняем элементу
21 maxValCol[RowN]:= ColN;//номер столбца приравняем текущему столбцу
22 end;
23 end;
24 end;
25 end;
Суммы элементов между диагоналями
Далее идут функции, осуществляющие подсчёт сумм элементов выше и ниже пересечения диагоналей, а так же смену местами этих элементов. Главной диагональю считается множество элементов матрицы, индексы которых совпадают, побочной диагональю считается та, которая идёт по диагонали из нижнего левого угла матрицы.
Функции GetSumAbove и GetSumBelow проходят соответствующие половины строк матрицы, для каждой строки высчитывая диапазон столбцов, из которых нужно суммировать элементы:
1 {возвращает сумму элементов выше пересечения диагоналей матрицы arr}
2 function GetSumAbove (const arr: TMatrix): Int64;
3 var
4 RowN, ColN: integer;
5 lastColumn: integer;//номер столбца, содержащего элемент дальней диагонали минус 1
6 begin
7 Result:= 0;
8 for RowN:= 0 to (high(arr) div 2) do
9 begin//с нулевой, по средюю строку
10 lastColumn:= high(arr)-RowN-1;//определим номер столбца последнего элемента, подлежащего суммированию
11 //если число столбцов меньше числа строк, то последний столбец может оказаться ближе
12 if lastColumn high(arr[RowN]) then lastColumn:= high(arr[RowN]);
13 for ColN:= RowN+1 to lastColumn do //просуммируем элементы в высчитаных пределах
14 Result:= Result + arr[RowN, ColN];
15 end;
16 end;
17 {возвращает сумму элементов ниже пересечения диагоналей матрицы arr}
18 function GetSumBelow(const arr: TMatrix): Int64;
19 var
20 RowN, ColN: integer;
21 lastColumn: integer;//номер столбца, содержащего элемент дальней диагонали минус 1
22 begin
23 Result:= 0;
24 for RowN:= (high(arr) div 2)+1 to high(arr) do
25 begin//со средней по последнюю строку
26 lastColumn:= RowN-1;//определим номер столбца последнего элемента, подлежащего суммированию
27 //если число столбцов меньше числа строк, то последний столбец может оказаться ближе
28 if lastColumn high(arr[RowN]) then lastColumn:= high(arr[RowN]);
29 for ColN:= high(arr)-RowN+1 to lastColumn do //просуммируем элементы в высчитаных пределах
30 Result:= Result + arr[RowN, ColN];
31 end;
32 end;
Процедура SwapAboveBelow таким же образом, как функция GetSumAbove , определяет, какие элементы лежат выше пересечения диагоналей, но не суммирует их, а каждый меняет местами с элементом того же столбца, симметричным текущему относительно верхней и нижней границ матрицы. Для смены используется вспомогательная процедура swap для целых чисел, определённая в этом же модуле:
1 {вспомогательная процедура: поменять местами два целых числа}
2 procedure swap(var first, second: integer);
3 var tmp: integer;
4 begin
5 tmp:= first;
6 first:= second;
7 second:= tmp;
8 end;
9 {поменять местами элементы выше и ниже пересечения диагоналей матрицы arr}
10 procedure SwapAboveBelow (var arr: TMatrix);
11 var
12 RowN, ColN: integer;
13 lastColumn: integer;//номер столбца, содержащего элемент дальней диагонали минус 1
14 begin
15 for RowN:= 0 to (high(arr) div 2) do
16 begin//с нулевой, по средюю строку
17 lastColumn:= high(arr)-RowN-1;//определим номер столбца последнего элемента, подлежащего суммированию
18 //если число столбцов меньше числа строк, то последний столбец может оказаться ближе
19 if lastColumn high(arr[RowN]) then lastColumn:= high(arr[RowN]);
20 for ColN:= RowN+1 to lastColumn do//для каждого элемента в высчитаных пределах
21 //поменяем его местами с элементом того же столбца, отстаящем на то же число строк, но от нижней границы матрицы
22 swap(arr[RowN, ColN], arr[high(arr) - RowN, ColN]);
23 end;
24 end;
Циклический сдвиг строк
Далее функция CircuarShift , осуществляющая циклический сдвиг строк матрицы вверх, или вниз. Направление сдвига определяется булевым параметром shiftUp, передаваемым процедуре:
1 {
2 осуществляет циклический сдвиг строк матрицы arr вверх при shiftUp = true,
3 и вниз, при shiftUp = false
4 }
5 procedure CircuarShift(var arr: TMatrix; shiftUp: boolean);
6 var
7 RowN: integer;
8 tmpRow: TVector;//временная переменная для хранения строки иатрицы
9
10 begin
11
12 if high(arr) 1 then exit;//если в матрице меньше двух строк - выходим
13 if shiftUp then
14 begin//если сдвиг вверх
15 tmpRow:= arr[high(arr)];//сохраним последнюю строку матрицы
16 arr[high(arr)]:= arr[0];//приравняем последнюю строку первой
17 for rowN:= 0 to high(arr)-2 do
18 begin//для строк с нулевой по пред-предпоследнюю
19 arr[rowN]:= arr[rowN+1];//текущая строка равна нижней
20 end;
21 arr[high(arr)-1]:= tmpRow;//предпоследнюю строку приравняем последней
22 end
23 else
24 begin//иначе, если сдвиг вниз
25 tmpRow:= arr[0];//сохраним нулвую строку
26 arr[0]:= arr[high(arr)];//приравняем нулевую строку последней
27 for rowN:= high(arr) downto 2 do
28 begin//для строк с последней по вторую
29 arr[RowN]:= arr[RowN-1];//текущая строка равна верхней
30 end;
31 arr[1]:= tmpRow;//первую строку приравняем нулевой
32 end;
33 end;
«Разворачивание» матрицы
Процедура UnwindMatrix осуществляет разворачивание матрицы в одномерный массив против часовой стрелки. Эта процедура в своих локальных переменных хранит координаты текущего элемента, текущее направление обхода (посредством перечислимого типа TDirection), а так же границы ещё не обойдённой части матрицы, которые сужаются каждый раз, когда проходится целая строка, или столбец. В этот же момент меняется направление обхода и текущим становится элемент в этом направлении. Обход завершается, когда число пройденных элементов станет равняться количеству элементов в матрице:
1 //перечисление - направления
2 type TDirection = (down, right, up, left);
3
4 {обходит матрицу arr против часовой стрелки и наполняет элементами массив res}
5 procedure UnwindMatrix(const arr: TMatrix; var res: TVector);
6 var
7 count, cur: integer;//число элементов в матрице и счётчик элементов
8
9 RowN, ColN: integer;
10 leftB, bottomB, rightB, topB: integer;//границы обхода - меняются при проходе полной строки или столбца
11 direction: TDirection;//текущее направление обхода
12
13 begin
14 if (length(arr) = 0) or (length(arr[0]) = 0) then exit;//если в матрице нет элементов - выходим
15 count:= length(arr) * length(arr[0]);//подсчитаем число элементов в матрице
16 SetLength(res, count);//выделим память для хранения всех элементов матрицы
17
18 //начальные условия обхода: текущий элемент [0,0], границы совпадают с граниуцами матриы, направление - вниз
19 direction:= down;
20 RowN:= 0;
21 ColN:= 0;
22 leftB:= 0;
23 bottomB:= high(arr);
24 rightB:= high(arr[0]);
25 topB:= 0;
26
27 for cur:= 0 to count-1 do
28 begin//пока не пройдём count элементов
29 res[cur]:= arr[RowN, ColN];//добавляем текущий элемент в массив
30 //дальненйшие действия зависят от текущего направления обхода
31 case direction of
32 down://если вниз
33 if RowN bottomB then inc(RowN)//если не дошли до нижней границы - сдвигаемся вниз
34 else
35 begin//иначе - прошли левый столбец
36 direction:= right;//сменим направление на вправо
37 inc(leftB);//сдвинем левую границу к центру
38 inc(ColN);//сдвинемся вправо
39 end;
40
41 right://если вправо
42 if ColN rightB then inc(ColN)//если не дошли до правой границы - сдвигаемся вправо
43 else
44 begin//иначе - прошли нижнюю строку
45 direction:= up;//сменим направление на вверх
46 dec(bottomB);//сдвинем нижнюю границу к центру
47 dec(RowN);//сдвинемся вверх
48 end;
49
50 up://если вверх
51 if RowN topB then dec(RowN)//если не дошли до верхней границы - сдвигаемся вверх
52 else
53 begin//иначе - прошли правый столбец
54 direction:= left;//сменим направление на влево
55 dec(rightB);//сдвинем правую границу к центру
56 dec(ColN);//сдвинемся влево
57 end;
58
59 left://если влево
60 if ColN leftB then dec(ColN)//если не дошли до левой границы - сдвигаемся влево
61 else
62 begin//иначе - прошли верхнюю строку
63 direction:= down;//сменим направление на вниз
64 inc(topB);//сдвинем верхнюю границу к центру
65 inc(RowN);//сдвинемся вниз
66 end;
67 end;
68 end;
69 end;
Сортировка строк матрицы
Наконец упорядочивание строк матрицы по убыванию суммы элементов каждой строки. Вспомогательная функция getRowSum возвращает сумму элементов заданной строки:
1 {возвращает сумму элементов RowN-ой строки матрицы arr}
2 function getRowSum(const arr: TMatrix; RowN: integer): Int64;
3 var ColN: integer;
4 begin
5 Result:= 0;
6 if RowN high(arr) then exit;//если в матрице нет RowN-ой строки - выходим
7 for ColN:= 0 to high(arr[RowN]) do//суммируем элементы строки
8 Result:= Result + arr[RowN, ColN];
9 end;
Сама сортировка осуществляется посредством процедуры SortRows . Был выбран алгоритм прямой вставки, так как число строк в матрице не предполагается большим, а этот алгоритм эффективен на небольших наборах данных. В любом случае сортировка осуществляется быстро, так как при перемене мест строк не происходит копирование данных, но просто переставляются местами указатели. Листинг этой функции:
1 {сортирует строки матрицы по убыванию сумм элементов каждой строки}
2 procedure SortRows(var arr: TMatrix);
3 var
4 i, k: integer;//переменные для алгоритма сортировки
5 tmpRow: TVector;//временная переменная для алгоритма сортировки
6 begin
7 //алгоритм сортировки методом прямой вставки
8 for i:= 1 to high(arr) do
9 begin//для строк с первой по последнюю
10 k:= i;//начиная с текущей строки
11 while (k 0) and (getRowSum(arr, k) getRowSum(arr, k-1)) do
12 begin//пока не дошли до нулевой строки, и сумма строки над текущей строкой больше текущей суммы
13 swap(arr[k-1], arr[k]);//поменяем текущую строку и строку над ней местами
14 dec(k);//сдвинемся вверх
15 end;
16 end;
17 end;
2.3.2 Модуль fileIO
Этот модуль содержит процедуры для файлового ввода/вывода матриц. Используются текстовые файлы, которые предварительно необходимо открыть и подготовить к чтению/записи.
Формат файла, содержащего матрицу таков: матрица записана построчно, начиная с первой строки, элементы в каждой строке записаны слева направо и разделены произвольным количеством пробелов. Именно такой файл создаёт процедура Write 2 DArray :
1 {
2 записывает матрицу arr в текстовый файл outFile. Файл должен быть
3 предварительно открыт
4 }
5 procedure Write2DArray(const arr: TMatrix; const outFile: TextFile);
6 var
7 rowN, colN: integer;
8 begin
9 for rowN:= low(arr) to high(arr) do
10 begin
11 for colN:= low(arr[rowN]) to high(arr[rowN]) do
12 begin
13 //ширина поля 12, так как -2147483648 - 11 символов
14 Write(outFile, arr[rowN, colN]: 12);
15 end;
16 Writeln(outFile);
17 end;
18 end;
Процедура Read 2 DArray читает файл по строкам, разбирая каждую строку на подстрока пробелами с помощью процедуры ExtractStrings:
1 { читает матрицу arr из текстового файла inFile. Файл должен быть
2 предварительно открыт}
3 procedure Read2DArray(var arr: TMatrix; const inFile: TextFile);
4 var
5 rowN, colN: integer;
6 colCount: integer; //максимальное количество чисел в строке (число столбцов матрицы)
7 lineStr: string; //текущая строка
8 strNumbers: TStringList;//текущая строка, разделённая на подстроки пробелами
9 begin
10 rowN:= 0;
11 colCount:= 0;
12 strNumbers:= TStringList.Create;
13 arr:= nil;
14 while not Eof(inFile) do
15 begin
16 Readln(inFile, lineStr);
17 strNumbers.Clear;
18 ExtractStrings([ ], [], PChar(lineStr), strNumbers); //разделим пробелами на подстроки
19 if colCount strNumbers.Count then colCount:= strNumbers.Count;
20 SetLength(arr, rowN+1, colCount);//выделим память под новую строку
21 for colN:= 0 to strNumbers.Count-1 do //для каждого числа в строке
22 arr[rowN, colN]:= StrToIntDef(strNumbers[colN], 0);
23 Inc(rowN);
24 end;
25 strNumbers.Destroy;
26 end;
2.3.3 Модуль form
Модуль, содержащий форму, переменную для хранения исходной матрицы, процедуры синхронизации содержания матрицы и элементов формы, а так же процедуру задания размеров матрицы.
Так как задача чётко разделена на задания, оперирующие одними и теми же исходными данными (целочисленным двумерным массивом), было принято решение разделить интерфейс приложения на две части. В верхней части формы отображается матрица исходных данных, которую можно редактировать и размеры которой можно менять. Нижняя часть формы представляет собой набор закладок, каждая из которых соответствует одной из поставленных задач. На каждой закладке содержится описание задания, кнопка «выполнить», а так же элементы, необходимы для отображения результата в рамках этого задания. Некоторые задания состоят в изменении исходной матрицы, результат выполнения таких заданий отображается непосредственно в исходных данных в верхней части формы. Всего существует как минимум три способа выбрать задачу: щёлкнуть мышкой по закладке, выбрать нужный пункт в меню «Задачи», нажать одну из кнопок F1 - F5.
Опишем важные процедуры формы. Процедура ReadMatrix осуществляет чтение исходных данных из таблицы на форме в двумерный массив. Перед началом чтения процедура устанавливает размер массива:
1 {заполнить матрицу в соответствии с содержанием таблицы на форме}
2 procedure TMainForm.ReadMatrix;
3 var rowN, colN: integer;
4 begin
5 SetLength(workMatrix, G_Matrix.RowCount-1, G_Matrix.ColCount-1);
6 for rowN:= 0 to G_Matrix.RowCount-2 do
7 for colN:= 0 to G_Matrix.ColCount-2 do
8 workMatrix[rowN, colN]:= StrToIntDef(G_Matrix.Cells[colN+1, rowN+1], 0);
9 end;
Процедура writeMatrix осуществляет обратную операцию, она заполняет поля таблицы в соответствии с массивом. Кроме этого она меняет значения числа строк и столбцов в соответствии с размерами массива:
1 {заполнить таблицу на форме в соответствии с содержанием матрицы}
2 procedure TMainForm.writeMatrix;
3 var rowN, colN: integer;
4 begin
5 G_Matrix.Cells[1, 1]:= ;//если матрица пуста
6 E_RowsN.Text:= IntToStr(high(workMatrix) + 1);
7 if(E_RowsN.Text 0) then
8 E_ColsN.Text:= IntToStr(high(workMatrix[low(workMatrix)]) + 1)
9 else E_ColsN.Text:= 0;
10 B_SetDimmsClick(self);
11 //заполним таблицу
12 for rowN:= low(workMatrix) to high(workMatrix) do
13 for colN:= low(workMatrix[rowN]) to high(workMatrix[rowN]) do
14 G_Matrix.Cells[colN+1, rowN+1]:= IntToStr(workMatrix[rowN, colN]);
15 end;
Процедура B_SetDimmsClick является обработчиком нажатия кнопки «задать размеры». Она проверяет, не стали ли размеры меньше единицы, меняет число строк и столбцов в таблицах формы, а так же проставляет номера строк и столбцов:
1 {обраюотчик уствновки размеров матрицы}
2 procedure TMainForm.B_SetDimmsClick(Sender: TObject);
3 var
4 i: integer;
5 RowsN, ColsN: integer;
6 begin
7 //значения размеров не должны быть меньше 1
8 RowsN:= StrToIntDef(E_RowsN.Text, 0);
9 if RowsN 1 then begin RowsN:= 1; E_RowsN.Text:= 1 end;
10 ColsN:= StrToIntDef(E_ColsN.Text, 0);
11 if ColsN 1 then begin ColsN:= 1; E_ColsN.Text:= 1 end;
12 //число строк и столбцов в таблице, учитывая колонку и строку с номерами
13 G_Matrix.RowCount:= RowsN + 1;
14 G_Matrix.ColCount:= ColsN + 1;
15 //в этих таблицах отображаются одномерные массивы из первого задания
16 G_Task1B.RowCount:= RowsN;
17 G_Task1C.RowCount:= RowsN;
18 //одномерный массив из четвёртого задания имеет длину, равную числу элементов исходной матрицы
19 G_Task4.ColCount:= RowsN * ColsN;
20 //расставим номера строк и столбцов
21 for i:= 0 to RowsN do
22 begin
23 G_Matrix.Cells[0, i+1]:= IntToStr(i+1);
24 G_Task1B.Cells[0, i]:= IntToStr(i+1);
25 G_Task1C.Cells[0, i]:= IntToStr(i+1);
26 end;
27 for i:= 0 to ColsN do
28 G_Matrix.Cells[i+1, 0]:= IntToStr(i+1);
29 for i:= 0 to RowsN * ColsN do
30 G_Task4.Cells[i, 0]:= IntToStr(i+1);
31 G_Matrix.Refresh;
32 end;
Процедура FormDestroy выполняется при уничтожении формы и выполняет очень важную функцию – освобождает память, которая выделялась во время работы приложения под матрицу исходных данных.
Процедура saveClick является обработчиком щелчка по пункту меню Файл-Сохранить. Она отображает диалог выбора файла для сохранения, создаёт выбранный файл, а после окончания записи закрывает его:
1 {обработчик Файл-Сохранить}
2 procedure TMainForm.saveClick(Sender: TObject);
3 var
4 outFile: TextFile;
5 begin
6 //отобразим диалог выбора файла для сохранения, если отмена - выходим
7 if SaveDialog.Execute = false then exit;
8 AssignFile(outFile, SaveDialog.Files[0]);
9 ReWrite(outFile);//создадим файл
10 readMatrix;//прочтём матрицу из таблицы
11 Write2DArray(workMatrix, outFile);//запишем матрицу в файл
12 CloseFile(outFile);//закроем файл.
Процедура loadClick ведёт себя так же, только не создаёт файл, а открывает его для чтения:
1 {обработчик Файл-Загрузить}
2 procedure TMainForm.loadClick(Sender: TObject);
3 var
4 inFile: TextFile;
5 begin
6 //отобразим диалог выбора фала для загрузки, если отмена - выходим
7 if OpenDialog.Execute = false then exit;
8 AssignFile(inFile, OpenDialog.Files[0]);
9 Reset(inFile);//подготовим файл к чтению
10 Read2DArray(workMatrix, inFile);//прочтём матрицу из файла
11 writeMatrix;//отобразим матрицу
12 CloseFile(inFile);//закроем файл
13 end;
Остальные процедуры просто вызывают процедуры и функции других модулей, наполняют результатами соответствующие заданию элементы формы, а в конце обязательно освобождают динамическую память, если таковая была выделена в рамках процедуры.
2.4 Описание формата исходных файлов
Матрица в исходном файле представляется в текстовом виде. Каждая строка матрицы начинается с новой строки. Каждый элемент строки отделён от других произвольным числом пробелов и должен быть представлен целым числом, лежащим в диапазоне [-2147483648; 2147483647]. Если какой-то элемент выходит за границы этого диапазона, либо не является целым числом, то он интерпретируется как ноль.
Пример правильно составленного исходного файла:
100000 10000 20000 40000 -4000
50 100 -20 1000 2000
-100 -50 -20 0 20
-1000 -200 200 2 12
4000 -100000 -40000 -10000 80000
3. Эксплуатационная документация
3.1 Описание применения
Программа предназначена для выполнения определённого набора операций над матрицами. Описание каждой операции можно прочесть на соответствующей вкладке в интерфейсе программы.
Программа предназначена для исполнения на IBM-совместимых компьютерах с операционной системой Windows (тестирование проводилось на Windows XP).
Минимальные системные требования:
· Дисплей с разрешением 1024x768
· Клавиатура
· 10 мегабайт свободной оперативной памяти
Требования приложения к оперативной памяти сильно зависят от размера обрабатываемой матрицы. Соответствующий минимальным требованиям компьютер сможет обрабатывать матрицы размером не менее ста элементов.
Входными параметрами для приложения являются файлы, описанные в пункте 3.4. Так же есть возможность ввести исходную матрицу непосредственно в таблицу на форме.
Выходные данные представляются в элементах формы, расположенных на соответствующей заданию вкладке (смотрите руководство оператора)
3.2 Руководство оператора
Интерфейс приложения разделён на две части. В верхней части формы отображается матрица исходных данных, которую можно редактировать и размеры которой можно менять. Нижняя часть формы представляет собой набор закладок, каждая из которых соответствует одной из поставленных задач. На каждой закладке содержится описание задания, кнопка «выполнить», а так же элементы, необходимы для отображения результата в рамках этого задания. Некоторые задания состоят в изменении исходной матрицы, результат выполнения таких заданий отображается непосредственно в исходных данных в верхней части формы. Всего существует как минимум три способа выбрать задачу: щёлкнуть мышкой по закладке, выбрать нужный пункт в меню «Задачи», нажать одну из кнопок F1 - F5.
Открытие файла с данными:

Выполнение задачи №1:

Результат выполнения задачи №1:

Переход к задаче №3:
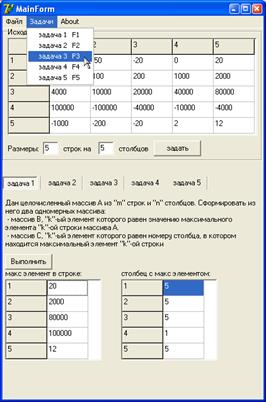
Выполнение задачи №3:
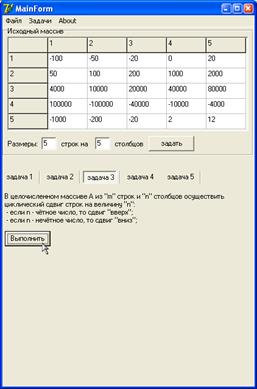
Результат двукратного выполнения задачи №3:

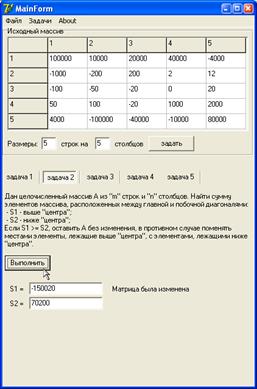
Результат выполнения задачи №2:
Результат выполнения задачи №5:

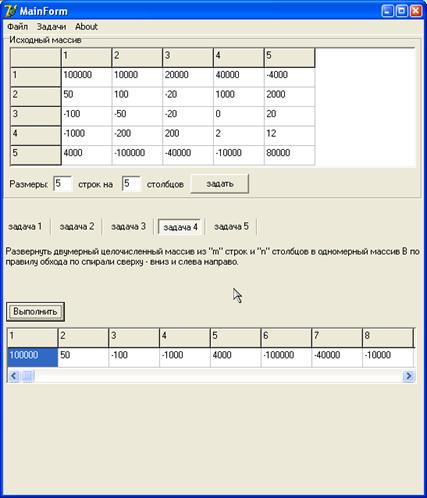
Результат выполнения задачи №4:
Сохранение полученной матрицы в файл:
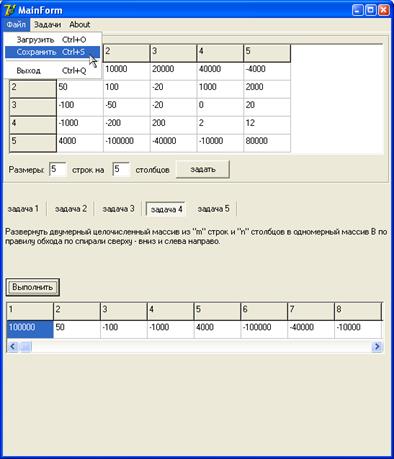
Завершение работы программы:

Содержание сохранённого файла:
100000 10000 20000 40000 -4000
50 100 -20 1000 2000
-100 -50 -20 0 20
-1000 -200 200 2 12
4000 -100000 -40000 -10000 80000
Выводы
Двумерный динамический массив – очень удобная конструкция для представления матрицы, размеры которой во время написания программы не известны. Но при его использовании нужно быть осторожным и учитывать некоторые особенности:
· При вызове SetLength с одним параметром размера будет выделена память только под первую размерность массива (например, будет увеличено число строк в матрице), остальные размерности затронуты не будут (в каждой добавленной строке будет ноль элементов).
· Каждый подмассив многомерного массива может иметь свою размерность (например, каждая строка матрицы в общем то может иметь длину, отличную от других)
· Необходимо всегда знать границы каждой размерности, чтобы не выйти за пределы массива в чужую память. Для этого полезны функции low и high .
· Необходимо всегда освобождать динамически выделенную память.
· При присваивании динамических массивов копирования данных не происходит, присваиваются лишь указатели, таким образом, после присваивания два массива будут указывать на одну и ту же область памяти. Чтобы получить копию массива, можно использовать функцию Copy.
· Copy копирует не весь многомерный массив, но только его первую размерность.
Приложения
Приложение 1. Тестовые примеры
Тест 1: Квадратная матрица 5 x 5.
Исходная матрица:
-100 -50 -20 0 20
50 100 200 1000 2000
4000 10000 20000 40000 80000
100000 -100000 -40000 -10000 -4000
-1000 -200 -20 2 12
Результат выполнения первого задания:
Максимальные элементы по строкам: 20; 2000; 80000; 100000; 12
Столбцы с максимальными элементами: 5; 5; 5; 1; 5
Результат выполнения второго задания:
S1 = 130
S2 = -40218
S1 S2, матрица не была изменена
Результат выполнения третьего задания:
Число столбцов нечётно – был произведён сдвиг «вниз»
-1000 -200 -20 2 12
-100 -50 -20 0 20
50 100 200 1000 2000
4000 10000 20000 40000 80000
100000 -100000 -40000 -10000 -4000
Результат выполнения четвёртого задания:
Матрица, «развёрнутая» против часовой стрелки: -100; 50; 4000; 100000; -1000; -200; -20; 2; 12; -4000; 80000; 2000; 20; 0; -20; -50; 100; 10000; -100000; -40000; -10000; 40000; 1000; 200; 20000
Результат выполнения пятого задания:
Строки отсортированы в невозрастающем порядке сумм:
4000 10000 20000 40000 80000
50 100 200 1000 2000
-100 -50 -20 0 20
-1000 -200 -20 2 12
100000 -100000 -40000 -10000 -4000
Тест 2: прямоугольная матрица 3 x 8.
Исходная матрица:
1 - 18 17 -16 15 -14 13 -12
-2 19 20 2000 200000 20000000 2000000000 11
3 -4 5 -6 7 -8 9 -10
Результат выполнения первого задания:
Максимальные элементы по строкам: 17; 2000000000; 9
Столбцы с максимальными элементами: 3; 7; 7
Результат выполнения второго задания:
S1 = -18 S2 = -4
S1 S2, матрица была изменена:
1 -4 17 -16 15 -14 13 -12
-2 19 20 2000 200000 20000000 2000000000 11
3 -18 5 -6 7 -8 9 -10
Результат выполнения третьего задания:
Число столбцов чётно – был произведён сдвиг «вверх»
-2 19 20 2000 200000 20000000 2000000000 11
3 -18 5 -6 7 -8 9 -10
1 -4 17 -16 15 -14 13 -12
Результат выполнения четвёртого задания:
Матрица, «развёрнутая» против часовой стрелки: 1; -2; 3; -4; 5; -6; 7; -8; 9; -10; 11; -12; 13; -14; 15; -16; 17; -18; 19; 20; 2000; 200000; 20000000; 2000000000;
Результат выполнения пятого задания:
Строки отсортированы в невозрастающем порядке сумм:
-2 19 20 2000 200000 20000000 2000000000 11
3 -4 5 -6 7 -8 9 -10
1 -18 17 -16 15 -14 13 -12
Тест 3: прямоугольная матрица 10 x 5, наполненная случайными числами.
Исходная матрица:
4490 6540 -12901 20330 -6046
-27459 -22256 26705 14852 -30502
23701 -11502 -30162 -14325 -20739
-15721 -14704 17504 -23934 21020
-27932 7054 -30557 -28698 -19302
-16794 -24715 28069 -2485 -11281
30727 18102 20673 -32373 23140
-16762 -1303 5821 21065 -25295
-24472 27091 -6385 -13002 -22009
-12309 26284 20788 -21316 -25044
Результат выполнения первого задания:
Максимальные элементы по строкам: 20330; 26705; 23701; 21020; 7054
Столбцы с максимальными элементами: 4; 3; 1; 5; 2
Результат выполнения второго задания:
S1 = 4934
S2 = -21774
S1 S2, матрица не была изменена
Результат выполнения третьего задания:
Число столбцов нечётно – был произведён сдвиг «вниз»
-12309 26284 20788 -21316 -25044
4490 6540 -12901 20330 -6046
-27459 -22256 26705 14852 -30502
23701 -11502 -30162 -14325 -20739
-15721 -14704 17504 -23934 21020
-27932 7054 -30557 -28698 -19302
-16794 -24715 28069 -2485 -11281
30727 18102 20673 -32373 23140
-16762 -1303 5821 21065 -25295
-24472 27091 -6385 -13002 -22009
Результат выполнения четвёртого задания:
Матрица, «развёрнутая» против часовой стрелки: 4490; -27459; 23701; -15721; -27932; -16794; 30727; -16762; -24472; -12309; 26284; 20788; -21316; -25044; -22009; -25295; 23140; -11281; -19302; 21020; -20739; -30502; -6046; 20330; -12901; 6540; -22256; -11502; -14704; 7054; -24715; 18102; -1303; 27091; -6385; -13002; 21065; -32373; -2485; -28698; -23934; -14325; 14852; 26705; -30162; 17504; -30557; 28069; 20673; 5821
Результат выполнения пятого задания:
Строки отсортированы в невозрастающем порядке сумм:
30727 18102 20673 -32373 23140
4490 6540 -12901 20330 -6046
-12309 26284 20788 -21316 -25044
-15721 -14704 17504 -23934 21020
-16762 -1303 5821 21065 -25295
-16794 -24715 28069 -2485 -11281
-27459 -22256 26705 14852 -30502
-24472 27091 -6385 -13002 -22009
23701 -11502 -30162 -14325 -20739
-27932 7054 -30557 -28698 -19302
Тест 4: матрица с большими по модулю числами.
Исходная матрица:
0 -2000000000 -2100000000 -2000000000 1
1000000000 -800000000 400000000 3 15
0 -2000000000 -2000000000 -2000000000 1
1000000000 -800000000 400000000 3 15
0 -2000000000 -2000000000 -2000000000 1
1000000000 -800000000 400000000 3 15
0 -2000000000 -1900000000 -200000000 1
Результат выполнения первого задания:
Максимальные элементы по строкам: 1; 1000000000; 1; 1000000000; 1; 1000000000; 1
Столбцы с максимальными элементами: 5; 1; 5; 1; 5; 1; 5
Результат выполнения второго задания:
S1 = -7699999981
S2 = -7499999981
S1 S2, матрица была изменена:
0 -2000000000 -1900000000 -2000000000 1
1000000000 -800000000 400000000 3 15
0 -2000000000 -2000000000 -2000000000 1
1000000000 -800000000 400000000 3 15
0 -2000000000 -2000000000 -2000000000 1
1000000000 -800000000 400000000 3 15
0 -2000000000 -2100000000 -2000000000 1
Результат выполнения третьего задания:
Число столбцов нечётно – был произведён сдвиг «вниз»
0 -2000000000 -1900000000 -2000000000 1
0 -2000000000 -2100000000 -2000000000 1
1000000000 -800000000 400000000 3 15
0 -2000000000 -2000000000 -2000000000 1
1000000000 -800000000 400000000 3 15
0 -2000000000 -2000000000 -2000000000 1
1000000000 -800000000 400000000 3 15
Результат выполнения четвёртого задания:
Матрица, «развёрнутая» против часовой стрелки: 0; 1000000000; 0; 1000000000; 0; 1000000000; 0; -2000000000; -1900000000; -2000000000; 1; 15; 1; 15; 1; 15; 1; -2000000000; -2100000000; -2000000000; -800000000; -2000000000; -800000000; -2000000000; -800000000; 400000000; 3; -2000000000; 3; -2000000000; 3; 400000000; -2000000000; 400000000; -2000000000
Результат выполнения пятого задания:
Строки отсортированы в невозрастающем порядке сумм:
1000000000 -800000000 400000000 3 15
1000000000 -800000000 400000000 3 15
1000000000 -800000000 400000000 3 15
0 -2000000000 -1900000000 -2000000000 1
0 -2000000000 -2000000000 -2000000000 1
0 -2000000000 -2000000000 -2000000000 1
0 -2000000000 -2100000000 -2000000000 1
Тест 5: матрица с ошибками.
Исходная матрица:
9999999999 123 fdf
456 rt 8888888888
1234567890 9876543210 789
q 0xf e
-77777777777 000 -13
915 -376 19
ddd -ddd 1111111111
Внутри программы такая матрица будет интерпретирована следующим образом:
0 123 0
456 0 0
1234567890 0 789
0 15 0
0 0 -13
915 -376 19
0 0 1111111111
Результат выполнения первого задания:
Максимальные элементы по строкам: 123; 456; 1234567890; 15; 0; 915; 1111111111
Столбцы с максимальными элементами: 2; 1; 1; 2; 1; 1; 3
Результат выполнения второго задания:
S1 = 123
S2 = 1111111130
S1 S2, матрица была изменена:
0 0 1111111111
456 0 19
1234567890 0 789
0 15 0
0 0 -13
915 -376 0
0 123 0
Результат выполнения третьего задания:
Число столбцов нечётно – был произведён сдвиг «вниз»
0 0 1111111111
0 123 0
456 0 0
1234567890 0 789
0 15 0
0 0 -13
915 -376 19
Результат выполнения четвёртого задания:
Матрица, «развёрнутая» против часовой стрелки: 0; 456; 1234567890; 0; 0; 915; 0; 0; 1111111111; 19; -13; 0; 789; 0; 0; 123; 0; 0; 15; 0; -376
Результат выполнения пятого задания:
Строки отсортированы в невозрастающем порядке сумм:
1234567890 0 789
0 0 1111111111
915 -376 19
456 0 0
0 123 0
0 15 0
0 0 -13
Приложение 2. Полный листинг формы (файл form . pas )
14 {
15 Модуль, содержащий форму, переменную для хранения исходной матрицы,
16 процедуры синхронизации содержания матрицы и элементов формы, а так же
17 процедуру задания размеров матрицы
18 }
19 unit form;
20
21 interface
22
23 uses
24 Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
25 Dialogs, Menus, StdCtrls, ExtCtrls, ComCtrls, Grids,
26 //модули программы
27 fileIO, MatrixOperations;
28
29 type
30 TMainForm = class(TForm)
31 Pages: TPageControl;
32 Task1: TTabSheet;
33 Task2: TTabSheet;
34 Task3: TTabSheet;
35 Task4: TTabSheet;
36 Task5: TTabSheet;
37 Menu: TMainMenu;
38 A1: TMenuItem;
39 load: TMenuItem;
40 save: TMenuItem;
41 N1: TMenuItem;
42 quit: TMenuItem;
43 N4: TMenuItem;
44 M_Task1: TMenuItem;
45 M_Task2: TMenuItem;
46 M_Task3: TMenuItem;
47 M_Task4: TMenuItem;
48 M_Task5: TMenuItem;
49 GroupBox1: TGroupBox;
50 G_Matrix: TStringGrid;
51 E_RowsN: TEdit;
52 Label1: TLabel;
53 Label2: TLabel;
54 E_ColsN: TEdit;
55 B_SetDimms: TButton;
56 SaveDialog: TSaveDialog;
57 OpenDialog: TOpenDialog;
58 Label3: TLabel;
59 Label4: TLabel;
60 G_Task1B: TStringGrid;
61 Label5: TLabel;
62 Label6: TLabel;
63 G_Task1C: TStringGrid;
64 B_Task1Run: TButton;
65 Label7: TLabel;
66 Label8: TLabel;
67 Label9: TLabel;
68 E_Task2S1: TEdit;
69 B_Task2Run: TButton;
70 E_Task2S2: TEdit;
71 L_Task2MatrxChanged: TLabel;
72 Label10: TLabel;
73 B_Task3Run: TButton;
74 L_Task3Result: TLabel;
75 Label11: TLabel;
76 B_Task4Run: TButton;
77 Label12: TLabel;
78 B_Task5Run: TButton;
79 about: TMenuItem;
80 MEM_Task4: TMemo;
81 procedure saveClick(Sender: TObject);
82 procedure loadClick(Sender: TObject);
83 procedure B_SetDimmsClick(Sender: TObject);
84 procedure FormCreate(Sender: TObject);
85 procedure quitClick(Sender: TObject);
86 procedure M_Task1Click(Sender: TObject);
87 procedure M_Task2Click(Sender: TObject);
88 procedure M_Task3Click(Sender: TObject);
89 procedure M_Task4Click(Sender: TObject);
90 procedure M_Task5Click(Sender: TObject);
91 procedure B_Task1RunClick(Sender: TObject);
92 procedure FormDestroy(Sender: TObject);
93 procedure B_Task2RunClick(Sender: TObject);
94 procedure B_Task3RunClick(Sender: TObject);
95 procedure B_Task4RunClick(Sender: TObject);
96 procedure B_Task5RunClick(Sender: TObject);
97 procedure aboutClick(Sender: TObject);
98 private
99 procedure readMatrix;
100 procedure writeMatrix;
101 public
102 published
103 { Public declarations }
104 end;
105
106 var
107 MainForm: TMainForm;
108 workMatrix: TMatrix;
109
110 implementation
111
112 uses Math;
113
114 {$R *.dfm}
115
116 {заполнить матрицу в соответствии с содержанием таблицы на форме}
117 procedure TMainForm.ReadMatrix;
118 var rowN, colN: integer;
119 begin
120 SetLength(workMatrix, G_Matrix.RowCount-1, G_Matrix.ColCount-1);
121 for rowN:= 0 to G_Matrix.RowCount-2 do
122 for colN:= 0 to G_Matrix.ColCount-2 do
123 workMatrix[rowN, colN]:= StrToIntDef(G_Matrix.Cells[colN+1, rowN+1], 0);
124 end;
125
126 {заполнить таблицу на форме в соответствии с содержанием матрицы}
127 procedure TMainForm.writeMatrix;
128 var rowN, colN: integer;
129 begin
130 G_Matrix.Cells[1, 1]:= ;//если матрица пуста
131 //обновим размеры матрицы
132 E_RowsN.Text:= IntToStr(high(workMatrix) + 1);
133 if(E_RowsN.Text 0) then
134 E_ColsN.Text:= IntToStr(high(workMatrix[low(workMatrix)]) + 1)
135 else E_ColsN.Text:= 0;
136 B_SetDimmsClick(self);
137 //заполним таблицу
138 for rowN:= low(workMatrix) to high(workMatrix) do
139 for colN:= low(workMatrix[rowN]) to high(workMatrix[rowN]) do
140 G_Matrix.Cells[colN+1, rowN+1]:= IntToStr(workMatrix[rowN, colN]);
141 end;
142
143 {обработчик Файл-Сохранить}
144 procedure TMainForm.saveClick(Sender: TObject);
145 var
146 outFile: TextFile;
147 begin
148 //отобразим диалог выбора файла для сохранения, если отмена - выходим
149 if SaveDialog.Execute = false then exit;
150 AssignFile(outFile, SaveDialog.Files[0]);
151 ReWrite(outFile);//создадим файл
152
153 readMatrix;//прочтём матрицу из таблицы
154 Write2DArray(workMatrix, outFile);//запишем матрицу в файл
155
156 CloseFile(outFile);//закроем файл
157
158 end;
159
160 {обработчик Файл-Загрузить}
161 procedure TMainForm.loadClick(Sender: TObject);
162 var
163 inFile: TextFile;
164 begin
165 //отобразим диалог выбора фала для загрузки, если отмена - выходим
166 if OpenDialog.Execute = false then exit;
167 AssignFile(inFile, OpenDialog.Files[0]);
168 Reset(inFile);//подготовим файл к чтению
169
170 Read2DArray(workMatrix, inFile);//прочтём матрицу из файла
171 writeMatrix;//отобразим матрицу
172
173 CloseFile(inFile);//закроем файл
174 end;
175
176 {обраюотчик уствновки размеров матрицы}
177 procedure TMainForm.B_SetDimmsClick(Sender: TObject);
178 var
179 i: integer;
180 RowsN, ColsN: integer;
181 begin
182 //значения размеров не должны быть меньше 1
183 RowsN:= StrToIntDef(E_RowsN.Text, 0);
184 if RowsN 1 then begin RowsN:= 1; E_RowsN.Text:= 1 end;
185 ColsN:= StrToIntDef(E_ColsN.Text, 0);
186 if ColsN 1 then begin ColsN:= 1; E_ColsN.Text:= 1 end;
187 //число строк и столбцов в таблице, учитывая колонку и строку с номерами
188 G_Matrix.RowCount:= RowsN + 1;
189 G_Matrix.ColCount:= ColsN + 1;
190 //в этих таблицах отображаются одномерные массивы из первого задания
191 G_Task1B.RowCount:= RowsN;
192 G_Task1C.RowCount:= RowsN;
193 //одномерный массив из четвёртого задания имеет длину, равную числу элементов исходной матрицы
194 //G_Task4.ColCount:= RowsN * ColsN;
195 //расставим номера строк и столбцов
196 for i:= 0 to RowsN do
197 begin
198 G_Matrix.Cells[0, i+1]:= IntToStr(i+1);
199 G_Task1B.Cells[0, i]:= IntToStr(i+1);
200 G_Task1C.Cells[0, i]:= IntToStr(i+1);
201 end;
202 for i:= 0 to ColsN do
203 G_Matrix.Cells[i+1, 0]:= IntToStr(i+1);
204
205 //for i:= 0 to RowsN * ColsN do
206 // G_Task4.Cells[i, 0]:= IntToStr(i+1);
207 G_Matrix.Refresh;
208 end;
209
210 {при создании формы задаём размер матрицы по умолчанию}
211 procedure TMainForm.FormCreate(Sender: TObject);
212 begin
213 B_SetDimmsClick(Sender);
214 end;
215
216 {при уничтожении формы освобождаем память, выделенную для хранения матрицы}
217 procedure TMainForm.FormDestroy(Sender: TObject);
218 begin
219 workMatrix:= nil;
220 end;
221
222 {обработчик Файл-Выход}
223 procedure TMainForm.quitClick(Sender: TObject);
224 begin
225 if mrYes = MessageDlg(Вы уверены, что хотите выйти?, mtConfirmation, [mbYes, mbNo], 0)
226 then Close;
227 end;
228
229 {обработчик Задачи-задача 1}
230 procedure TMainForm.M_Task1Click(Sender: TObject);
231 begin
232 Pages.ActivePageIndex:= 0;
233 end;
234 {обработчик Задачи-задача 2}
235 procedure TMainForm.M_Task2Click(Sender: TObject);
236 begin
237 Pages.ActivePageIndex:= 1;
238 end;
239 {обработчик Задачи-задача 3}
240 procedure TMainForm.M_Task3Click(Sender: TObject);
241 begin
242 Pages.ActivePageIndex:= 2;
243 end;
244 {обработчик Задачи-задача 4}
245 procedure TMainForm.M_Task4Click(Sender: TObject);
246 begin
247 Pages.ActivePageIndex:= 3;
248 end;
249 {обработчик Задачи-задача 5}
250 procedure TMainForm.M_Task5Click(Sender: TObject);
251 begin
252 Pages.ActivePageIndex:= 4;
253 end;
254
255 {выполнение первого задания}
256 procedure TMainForm.B_Task1RunClick(Sender: TObject);
257 var
258 maxVal: TVector; //массив максимальных элементов из каждой строки
259 maxValCol: TVector; //массив номеров столбцов с максимальными элементами
260 RowN: integer;
261 begin
262 readMatrix;//прочитаем матрицу из таблицы
263 GetMaxVals(maxVal, maxValCol, workMatrix);//сформируем массивы по заданию
264 for RowN:= low(maxVal) to high(maxVal) do
265 begin//выведем сформированные массивы в элементы формы
266 G_Task1B.Cells[1, RowN]:= IntToStr(maxVal[RowN]);
267 G_Task1C.Cells[1, RowN]:= IntToStr(maxValCol[RowN]+1);
268 end;
269 //освободим память
270 maxVal:= nil;
271 maxValCol:= nil;
272 end;
273
274 {выполнение второго задания}
275 procedure TMainForm.B_Task2RunClick(Sender: TObject);
276 var S1, S2: Int64;//суммы выше и ниже пересечения диагоналей
277 begin
278 readMatrix;//проситаем матрицу из таблицы
279 //высчитаем суммы
280 S1:= GetSumAbove(workMatrix);
281 S2:= GetSumBelow(workMatrix);
282 //выведем суммы в элементы формы
283 E_Task2S1.Text:= IntToStr(S1);
284 E_Task2S2.Text:= IntToStr(S2);
285 if S1 = S2 then L_Task2MatrxChanged.Caption:= Матрица не была изменена
286 else
287 begin//если S1 S2, то
288 SwapAboveBelow(workMatrix);//меняем местами элементы выше и ниже пересечения диагоналей
289 writeMatrix;//выводим изменённую матрицу на форму
290 L_Task2MatrxChanged.Caption:= Матрица была изменена
291 end;
292 end;
293
294 {выполнение третьего задания}
295 procedure TMainForm.B_Task3RunClick(Sender: TObject);
296 begin
297 readMatrix;//прочтём матрицу из таблицы
298 if (high(workMatrix)+1) mod 2 = 0 then
299 begin//если число строк - чётное
300 CircuarShift(workMatrix, true);//осуществим циклический сдвиг вверх
301 L_Task3Result.Caption:= был произведён сдвиг вверх;
302 end
303 else
304 begin//иначе, если число строк - нечётное
305 CircuarShift(workMatrix, false);//осуществим циклический сдвиг вниз
306 L_Task3Result.Caption:= был произведён сдвиг вниз;
307 end;
308 writeMatrix;//выведем изменённую матрицу в таблицу
309 end;
310
311 {выполнение четвёртого задания}
312 procedure TMainForm.B_Task4RunClick(Sender: TObject);
313 var arrayB: TVector;//массив, содержащий развёрнутую матрицу
314 var i: integer;
315 begin
316 readMatrix;//прочтём матрицу из таблицы
317 UnwindMatrix(workMatrix, arrayB);//наполним массив, обходя матрицу по спирали
318 MEM_Task4.Lines[0]:= ;
319 for i:= 0 to high(arrayB) do
320 begin//выведем все элементы из массива на форму
321 //G_Task4.Cells[i, 1]:= IntToStr(arrayB[i]);
322 MEM_Task4.Lines[0]:= MEM_Task4.Lines[0] + IntToStr(arrayB[i]) + ;
323 end;
324 arrayB:= nil;//освободим память
325 end;
326
327 {выполнение пятого задания}
328 procedure TMainForm.B_Task5RunClick(Sender: TObject);
329 begin
330 readMatrix;//прочтём матрицу из таблицы
331 SortRows(workMatrix);//отсортируем строки матрицы по убыванию сумм
332 writeMatrix;//выведем матрицу в таблицу
333 end;
334 {обработчик About}
335 procedure TMainForm.aboutClick(Sender: TObject);
336 var info: string;
337 begin
338 info:= Курсовая работа по дисциплине Программирование на ЯВУ#10#10 +
339 Тема: Работа с двумерными числовыми массивами#10 +
340 Выполнил: студент группы ВСМ-06-08 Филон Д. В.#10#10#10 +
341 #9#9#9#9#9#9Москва 2010 год;
342 MessageDlg(info, mtInformation, [mbIgnore], 0);
343 end;
344 end.