Расчет авиационного поршневого двигателя
СОДЕРЖАНИЕ: Министерство образования и науки Украины Национальный аэрокосмический университет им. Н.Е. Жуковского “ХАИ” Расчетно-пояснительная записка к курсовому проекту по дисциплинеМинистерство образования и науки Украины
Национальный аэрокосмический университет
им. Н.Е. Жуковского “ХАИ”
Расчетно-пояснительная записка к курсовому проекту по дисциплине
“Авиационные двигатели”
Харьков 2008
Содержание
1.2 Выбор дополнительных исходных данных
1.3 Расчет процесса наполнения
1.6 Расчёт процесса расширения
1.7 Определение индикаторных параметров двигателя
1.8 Определение эффективных параметров двигателя
1.9 Определение геометрических параметров двигателя
2.3 Разнос масс КШМ с прицепными шатунами
2.5 Построение верхней петли индикаторной диаграммы
2.6 Суммарная сила, действующая на поршень
2.7 Силы, действующие в центральном КШМ
2.8 Суммарные радиальные и окружные силы действующие на шатунную шейку
4. Расчет на прочность коленчатого вала
4.1 Силы, действующие на колено коленчатого вала
4.2 Определение запаса прочности в шатунной шейке
4.3 Определение запаса прочности в коренной шейке
Список использованной литературы
1. Тепловой расчет
Под тепловым расчетом поршневого двигателя внутреннего сгорания подразумевается определение параметров, характеризующих рабочие процессы двигателя, а так же величин, определяющих энергетические и экономические параметры его работы.
По данным расчета и по заданным мощности и частоте вращения коленчатого вала можно определить основные размеры проектируемого двигателя. Кроме того, по данным теплового расчета с достаточной для практики точностью можно построить индикаторную диаграмму, необходимую для определения газовых сил, действующих на поршень двигателя, на стенки и головку цилиндра, на элементы кривошипно-шатунного механизма.
1.1 Исходные данные
1) Эффективная мощность на расчетной высоте –![]() .
.
2) Частота вращения коленчатого вала – ![]() .
.
3) Число цилиндров – ![]() .
.
4) Степень сжатия – ![]() .
.
5) Давление наддува – ![]() .
.
6) Расчетная высота – ![]() .
.
7) Прототип двигателя – АИ-26.
1.2 Выбор дополнительных исходных данных
1. Коэффициент избытка воздуха принимаем равным ![]() .
.
2. Топливо. Сорт применяемого топлива зависит от степени сжатия и давления наддува. В нашем случае (относительно невысокая степень сжатия) наиболее подходящим является бензин Б-91/115.
Низшую теплотворную способность топлива определим по формуле
![]() .
.
Элементарный состав авиабензина Б-91/115 включает в себя: ![]() ;
; ![]() ;
; ![]() , средняя молекулярная масса –
, средняя молекулярная масса – ![]() . Тогда:
. Тогда:
![]()
3. Параметры воздуха на расчетной высоте.
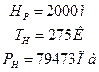
1.3 Расчет процесса наполнения
Цель расчета процесса наполнения – определение давления ![]() и температуры
и температуры ![]() свежего заряда в конце хода выпуска.
свежего заряда в конце хода выпуска.
1. Согласно заданию давление наддува ![]() . Находим температуру воздуха в конце такта наполнения
. Находим температуру воздуха в конце такта наполнения
![]() ,
,
где ![]() - повышение температуры воздуха в нагнетателе. Адиабатическая работа сжатия 1кг воздуха равна:
- повышение температуры воздуха в нагнетателе. Адиабатическая работа сжатия 1кг воздуха равна:
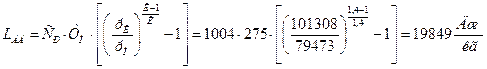 .
.
Адиабатический КПД центробежного нагнетателя примем равным ![]() .
.
Тогда:
![]() ;
;
![]() .
.
2. Определяем коэффициент наполнения двигателя с наддувом на расчетной высоте
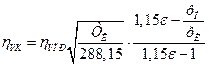 ,
,
где ![]() - приведенный коэффициент наполнения.
- приведенный коэффициент наполнения.
Примем ![]() , тогда
, тогда
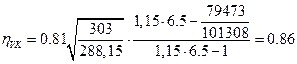 .
.
3. Находим давление в конце такта наполнения.
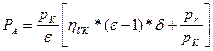 ,
,
где pr – давление остаточных газов в конце такта наполнения. Принимаем:
![]() .
.
Степень подогрева свежей смеси в процессе наполнения ![]() условно характеризует результат суммарного теплообмена смеси со стенками цилиндра и донышком поршня, а также понижение температуры за счет испарения топлива.
условно характеризует результат суммарного теплообмена смеси со стенками цилиндра и донышком поршня, а также понижение температуры за счет испарения топлива.
При ![]() ,
,![]() . Тогда:
. Тогда:
![]() .
.
После подстановки найденных и полученных величин получим
![]() .
.
4. Определяем коэффициент остаточных газов
![]() ,
,
где ![]() - температура остаточных газов.
- температура остаточных газов.
Примем ![]() , тогда:
, тогда:
![]() .
.
5. Находим температуру газов в конце такта впуска
![]() .
.
1.4 Расчет процесса сжатия
Цель расчета процесса сжатия – определение давления ![]() и температуры
и температуры ![]() газов в конце этого процесса.
газов в конце этого процесса.
1. Давление в конце такта сжатия:
![]()
2. Температура в конце такта сжатия:
![]()
1.5 Расчет процесса сгорания
Цель расчета процесса сгорания – определение максимальных значений давления ![]() и температуры
и температуры ![]() газов при сгорании топлива.
газов при сгорании топлива.
1. Температура ![]() газов определим из уравнения сгорания, полученного на основании первого принципа термодинамики:
газов определим из уравнения сгорания, полученного на основании первого принципа термодинамики:
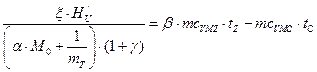 ,
,
где ![]() - низшая теплота сгорания топлива с учетом условий, при которых протекает процесс сгорания.
- низшая теплота сгорания топлива с учетом условий, при которых протекает процесс сгорания.
![]() ;
;
![]() - коэффициент эффективного выделения теплоты. Примем
- коэффициент эффективного выделения теплоты. Примем ![]() ;
;
![]() – теоретически необходимое количество воздуха для сгорания
– теоретически необходимое количество воздуха для сгорания ![]() топлива.
топлива.
![]()
Действительное количество воздуха для сгорания 1кг топлива будет составлять:
![]() .
.
![]() - действительный коэффициент молекулярного изменения, где
- действительный коэффициент молекулярного изменения, где ![]() - химический коэффициент молекулярного изменения.
- химический коэффициент молекулярного изменения.
Для случая ![]() определяем
определяем
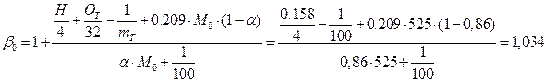 .
.
Тогда:
![]() .
.
![]() - средняя молярная теплоемкость газов в интервале температур от 0 до
- средняя молярная теплоемкость газов в интервале температур от 0 до ![]() .
.
![]()
Тогда
![]() .
.
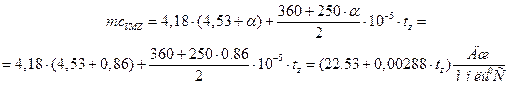
Подставим все известные величины в исходное уравнение:
![]()
Решим данное уравнение с помощью программного пакета MathCAD 13.
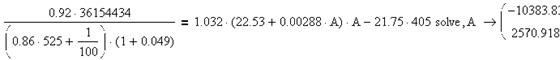
Расчет температуры ![]() в пакете MathCAD 13
в пакете MathCAD 13
В результате получим: ![]() ,
, ![]()
2. Определим максимальное давление сгорания
![]()
1.6 Расчёт процесса расширения
Цель расчёта процесса расширения – определение давления ![]() и температуры
и температуры ![]() в конце такта расширения.
в конце такта расширения.
1. Находим давление в конце такта расширения:
![]()
2.Находим температуру в конце такта расширения:
![]()
1.7 Определение индикаторных параметров двигателя
1. Индикаторное давление
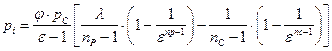 ,
,
где ![]() - коэффициент полноты (скругления) индикаторной диаграммы. Примем
- коэффициент полноты (скругления) индикаторной диаграммы. Примем ![]() .
.
![]() - степень повышения давления.
- степень повышения давления.
Тогда:
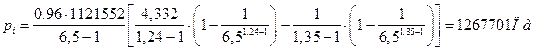
2. Определяем индикаторный КПД.
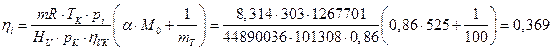
3. Удельный индикаторный расход топлива равен
![]() .
.
1.8 Определение эффективных параметров двигателя
1. Среднее эффективное давление
![]() ,
,
где 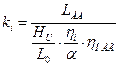 - коэффициент, оценивающий долю индикаторной мощности, затраченной на привод нагнетателя.
- коэффициент, оценивающий долю индикаторной мощности, затраченной на привод нагнетателя.
Эффективный КПД нагнетателя:
![]()
![]() - теоретически необходимое количество воздуха для сгорания 1кг топлива,
- теоретически необходимое количество воздуха для сгорания 1кг топлива, ![]() .
.
Тогда
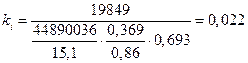 .
.
Среднее давление механических потерь ![]() характеризует мощность, затраченную на преодоление сил трения, на привод вспомогательных механизмов и агрегатов и на “насосные” потери.
характеризует мощность, затраченную на преодоление сил трения, на привод вспомогательных механизмов и агрегатов и на “насосные” потери.
Для определения ![]() пользуются эмпирическими уравнениями, полученными на основании экспериментальных данных.
пользуются эмпирическими уравнениями, полученными на основании экспериментальных данных.
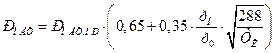 ,
,
где ![]()
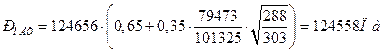
Среднее эффективное давление:
![]()
2. Механический КПД
![]()
3. Значение эффективного КПД
![]()
4. Удельный эффективный расход топлива
![]()
1.9 Определение геометрических параметров двигателя
1. Рабочий объем цилиндра двигателя
![]()
2. Определяем диаметр цилиндра ![]() и ход поршня
и ход поршня ![]() . Обозначим отношение
. Обозначим отношение ![]() . Тогда
. Тогда ![]() , откуда
, откуда ![]() .
.
Значение m принимаем по прототипу ![]() .
.
![]() .
.
3. Ход поршня ![]() .
.
4. Общий рабочий объем двигателя ![]()
5. Проверяем правильность расчетов основных размеров двигателя
![]() .
.
2. Динамический расчет
Цель динамического расчета состоит в построении по данным теплового расчета индикаторной диаграммы и нахождении сил, действующих на все звенья кривошипно-шатунного механизма.
Выполнение динамического расчета авиационного поршневого двигателя связано с довольно большим объемом расчетной работы, поэтому целесообразно проводить его на ЭВМ. Особенность такого расчета – учет в нем главного динамического эффекта, создаваемого прицепными механизмами, - сил второго порядка. Динамический расчет звездообразного двигателя без учета этих сил неприемлем, поскольку при этом создается ложное впечатление об уравновешенности механизма и о запасах прочности коленчатого вала, редуктора и воздушного винта.
2.1 Допущения
1. Учитываем только силы избыточного давления газов на поршень и силы инерции КШМ.
2. Индикаторные диаграммы во всех цилиндрах считаем одинаковыми. Теоретические диаграммы корректируем только в точке, соответствующей концу сгорания.
В конце сжатия и расширения диаграммы не корректируем. Считаем, что в течение насосных ходов газовые силы пренебрежимо малы по сравнению с силами инерции КШМ. Поэтому в тактах всасывания и выхлопа газовые силы считаем равными нулю.
3. Предполагаем геометрическое подобие деталей КШМ проектируемого двигателя и прототипа.
4. Для расчета сил инерции реальное распределение масс в КШМ приводим к расчетной схеме, в которой все массы считаем точечными, сосредоточенными на осях поршневых пальцев и оси шатунной шейки коленчатого вала.
5. Приведенные массы поступательно-движущихся частей в цилиндре с главным и прицепным шатунами считаем одинаковыми.
6. Отличия в кинематике и динамике прицепных механизмов от центрального не учитываем вплоть до заключительного этапа динамического расчета. На заключительном этапе динамического расчета учитываем главный динамический эффект, создаваемый прицепными механизмами.
2.2 Определение основных размеров КШМ
Схема кривошипно-шатунного механизма с прицепными шатунами показана на рисунке 2.
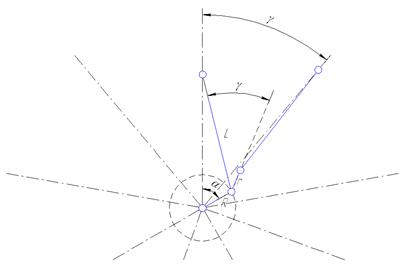
Рисунок 2 Схема кривошипно-шатунного механизма с прицепными шатунами.
Ход поршня ![]() и радиус кривошипа
и радиус кривошипа ![]() найдены в тепловом расчете.
найдены в тепловом расчете.
Основные размеры центрального КШМ вполне определяются радиусом ![]() и длиной шатуна
и длиной шатуна ![]() . Отношение
. Отношение ![]() принимаем таким же как и у прототипа,
принимаем таким же как и у прототипа, ![]() . Тогда длина шатуна:
. Тогда длина шатуна:
![]() .
.
Угол прицепа:
![]()
Радиусы прицепов ![]() прицепных шатунов в различных цилиндрах неодинаковы. Из условия геометрического подобия следует, что
прицепных шатунов в различных цилиндрах неодинаковы. Из условия геометрического подобия следует, что
![]() .
.
В звездообразных двигателях при одинаковой длине прицепных шатунов всегда минимальным получается радиус прицепа шатунов, которые работают в цилиндрах, противоположных главному. Для семицилиндровых двигателей – это 4-й и 5-й цилиндры. Длину прицепного шатуна определяем по формуле:
![]() ,
,
где ![]() - угол между плоскостью симметрии главного шатуна и rmin
.
- угол между плоскостью симметрии главного шатуна и rmin
.
![]() .
.
Радиус остальных прицепов находим по формуле:
![]() , где
, где ![]() .
.
![]()
Результаты расчета сводим в таблицу 1
Таблица 1 Радиусы прицепов шатунов
| 1 | 2 | 3 | |
| 0,078 | 0,79 | 0,076 |
2.3 Разнос масс КШМ с прицепными шатунами
1. Каждый прицепной шатун заменяют двумя массами, одна из которых ![]() сосредотачивается на оси поршневого пальца, а другая
сосредотачивается на оси поршневого пальца, а другая ![]() – на оси прицепного шатуна.
– на оси прицепного шатуна.
2. Под “приведенным” главным шатуном (рисунок 3) понимают собственно главный шатун плюс массы пальцев прицепных шатунов ![]() и массы
и массы ![]() , сосредоточенные на осях этих пальцев. Обозначим
, сосредоточенные на осях этих пальцев. Обозначим![]() ;
; ![]() . Приведенный главный шатун заменяем массами МПШ
, сосредоточенной на оси поршневого пальца, и
. Приведенный главный шатун заменяем массами МПШ
, сосредоточенной на оси поршневого пальца, и ![]() , сосредоточенной на оси шатунной шейки. Величины
, сосредоточенной на оси шатунной шейки. Величины ![]() и
и ![]() определяем из формул:
определяем из формул:
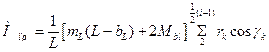 ,
,
![]() .
.
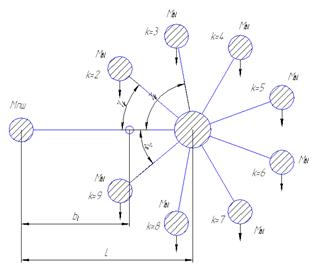
Рисунок 3 – Схема приведения масс главного шатуна.
3. Приведенная масса поступательно-движущихся частей.
Эта масса различна в цилиндрах с главным шатуном и с прицепным.
В цилиндре с прицепным шатуном
![]() ,
,
где ![]() – масса комплекта поршня;
– масса комплекта поршня;
![]() – часть массы прицепного шатуна, отнесенная к оси поршневого пальца.
– часть массы прицепного шатуна, отнесенная к оси поршневого пальца.
В цилиндре с главным шатуном
![]()
4. Приведенная масса вращательно-движущихся частей
![]() ,
,
где ![]() - масса вращательно-движущихся частей;
- масса вращательно-движущихся частей;
![]() - часть массы шатуна;
- часть массы шатуна;
![]() – приведенная масса кривошипа.
– приведенная масса кривошипа.
2.4 Силы инерции
Силы инерции поступательно-движущихся масс переменны по величине и направлению и действуют по осям цилиндров. Силу инерции в цилиндре с главным шатуном находят из уравнения:
![]() ,
,
а силу инерции в цилиндре с прицепным шатуном – из уравнения:
![]() ,
,
где ![]() - ускорения масс
- ускорения масс ![]() и
и ![]() .
.
Силы инерции вращательно-движущихся масс находят по формулам:
![]() ,
,
![]() .
.
Силы ![]() , постоянные по модулю, приложены к оси шатунной шейки и направлены по радиусу кривошипа.
, постоянные по модулю, приложены к оси шатунной шейки и направлены по радиусу кривошипа.
2.5 Построение верхней петли индикаторной диаграммы
Согласно принятым ранее допущениям считаем, что в такте наполнения и выхлопа разность абсолютных давлений в цилиндре и картере равна нулю. Абсолютные давления в тактах сжатия и расширения меняются по политропам. Сгорание происходит при постоянном объеме. В конце сгорания давление составляет 0.85 от расчетного. Расширение заканчивается скачкообразным падением давления в НМТ от расчетного ![]() до давления в картере
до давления в картере ![]() .
.
Таким образом, расчету подлежат только давления в ходе расширения и сжатия, определяемые по формуле:
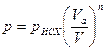 ,
,
где ![]() - давление в НМТ;
- давление в НМТ;
![]() – полный объем цилиндра,
– полный объем цилиндра,
![]()
![]() – текущий объем над поршнем,
– текущий объем над поршнем,
![]() ,
,
где ![]()
![]() – показатель политропы (в процессе сжатия
– показатель политропы (в процессе сжатия ![]() , в процессе расширения
, в процессе расширения ![]() ). После подстановки получим:
). После подстановки получим:
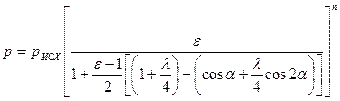 .
.
Вычисления выполнены с помощью пакета Microsoft EXCEL, полученные данные занесены в таблицу 1
Таблица 1 – Давления и объемы в ходе расширения и сжатия
| Сжатие | Расширение | ||||
| 180 | 89267 | 0,00312 | 360 | 1119735 | 0,00048 |
| 190 | 86819 | 0,00318 | 370 | 862225 | 0,00058 |
| 200 | 80365 | 0,00337 | 380 | 488627 | 0,00089 |
| 210 | 72102 | 0,00365 | 390 | 273784 | 0,00136 |
| 220 | 64068 | 0,00399 | 400 | 167575 | 0,00196 |
| 230 | 57477 | 0,00432 | 410 | 113280 | 0,00261 |
| 240 | 52823 | 0,00460 | 420 | 83752 | 0,00327 |
| 250 | 50251 | 0,00477 | 430 | 66934 | 0,00386 |
| 260 | 49855 | 0,00480 | 440 | 57259 | 0,00433 |
| 270 | 51896 | 0,00466 | 450 | 52023 | 0,00465 |
| 280 | 57000 | 0,00435 | 460 | 49884 | 0,00480 |
| 290 | 66478 | 0,00388 | 470 | 50197 | 0,00478 |
| 300 | 82961 | 0,00329 | 480 | 52692 | 0,00461 |
| 310 | 111869 | 0,00264 | 490 | 57271 | 0,00433 |
| 320 | 164913 | 0,00198 | 500 | 63797 | 0,00400 |
| 330 | 268448 | 0,00138 | 510 | 71794 | 0,00367 |
| 340 | 477973 | 0,00090 | 520 | 80081 | 0,00338 |
| 350 | 847071 | 0,00059 | 530 | 86642 | 0,00319 |
| 360 | 1119735 | 0,00048 | 540 | 89265 | 0,00312 |
2.6 Суммарная сила, действующая на поршень
Под суммарной силой, действующей на поршень, понимают сумму газовой силы и силы инерции
![]() ,
,
где ![]() - сила давления газов на поршень,
- сила давления газов на поршень, ![]()
![]() - абсолютное давление в цилиндре,
- абсолютное давление в цилиндре,
![]() - абсолютное давление в картере,
- абсолютное давление в картере,
![]() - сила инерции поступательно-движущихся масс.
- сила инерции поступательно-движущихся масс.
2.7 Силы, действующие в центральном КШМ
В центральном КЩМ действуют силы, показанные на рисунке 4. Причем они имеют положительные значения. При направлении, противоположном указанному, силы считают отрицательными. Они равны:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
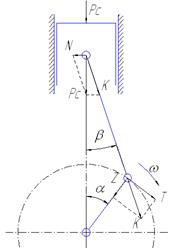
Рисунок 4 – Силы, действующие в центральном КШМ.
2.8 Суммарные радиальные и окружные силы действующие на шатунную шейку
На шатунную шейку звездообразного двигателя действуют силы каждого цилиндра одновременно. Складываясь, они дают суммарную радиальную силу ![]() и суммарную касательную силу
и суммарную касательную силу ![]() . Для получения
. Для получения ![]() и
и ![]() нужно сложить силы
нужно сложить силы ![]() , а затем силы
, а затем силы ![]() каждого цилиндра, действующие в каждый момент поворота кривошипа коленчатого вала.
каждого цилиндра, действующие в каждый момент поворота кривошипа коленчатого вала.
Поскольку индикаторный процесс во всех цилиндрах предполагают одинаковым и силы инерции одинаковы, то силы ![]() и
и ![]() в различных цилиндрах оказываются сдвинутыми одна относительно другой по фазе на угол
в различных цилиндрах оказываются сдвинутыми одна относительно другой по фазе на угол ![]() .
.
На шейку кривошипа дополнительно к ![]() действует в радиальном направлении центробежная сила
действует в радиальном направлении центробежная сила ![]() вращательно-движущихся масс шатуна
вращательно-движущихся масс шатуна ![]() .
.
На щеки коленчатого вала действует в радиальном направлении дополнительно к силе ![]() центробежная сила
центробежная сила ![]() , возникшая в результате вращения массы
, возникшая в результате вращения массы ![]() .
.
Динамический расчет выполнен на ЭВМ. Это позволило значительно упростить процедуру расчета, а вместе с тем и повысить его точность. Результаты вычисления суммарных окружных и радиальных сил отображены в таблице 2; полных сил, действующих на шатунную шейку в окружном и в радиальном направлениях – в таблице 3.
Результаты расчета избыточного (Р) и абсолютного (PR) давления газов на поршень, силы инерции поступательно-движущихся частей (F), силы, действующей по оси цилиндра (PS), нормально к оси цилиндра (NS), окружной силы от одного цилиндра (Т) и радиальной силы от одного цилиндра (ZS) помещены в таблице 4.
Параметры ввода
Число цилиндров 7
Число однорядных звезд, ![]() .
.
Число прицепных шатунов, ![]() .
.
Частота вращения коленчатого вала, ![]() .
.
Степень сжатия, ![]() .
.
Ход поршня, ![]() .
.
Диаметр цилиндра, ![]() .
.
Отношение радиуса к длине главного шатуна, ![]() .
.
Радиус прицепа шатунов, ![]() .
.
Давление в конце pасшиpения, ![]() .
.
Давление в конце наполнения, ![]() .
.
Атмосферное давление, ![]() .
.
Показатель политpопы сжатия, ![]() .
.
Показатель политpопы pасшиpения, ![]() .
.
Таблица 2 – Суммарные окружные и радиальные силы.
-----------------------------------------------
| TC | ZC | ZCD |
-----------------------------------------------
| 24334.54000| -28539.68000| -28539.68000|
| 16694.21000| -34419.33000| -34419.33000|
| 10324.36000| -34938.66000| -28069.61000|
| 8007.59900| -25581.32000| -25581.32000|
| 9021.97900| -24514.77000| 27376.85000|
| 26920.21000| 28033.34000| 28033.34000|
| 33954.51000| 4737.10500| 4564.03100|
| 31262.81000| -15762.70000| -15762.70000|
-----------------------------------------------
Таблица 3 - Полные силы действующие на шатунную шейку
в окружном и в радиальном направлениях.
| Угол| TSI | ZSI | ZSID |
--------------------------------------------------------
|.00|.24335E+05 | -.20928E+05 | -.20928E+05 |
| 12.86|.15000E+05 | -.26998E+05 | -.26998E+05 |
| 25.71|.70217E+04 | -.28081E+05 | -.21212E+05 |
| 38.57|.32616E+04 | -.19630E+05 | -.19630E+05 |
| 51.43|.30707E+04 | -.19769E+05 |.32123E+05 |
| 64.29|.20062E+05 |.31336E+05 |.31336E+05 |
| 77.14|.26533E+05 |.64309E+04 |.62579E+04 |
| 90.00|.23651E+05 | -.15763E+05 | -.15763E+05 |
|102.86|.16913E+05 | -.30233E+05 | -.30233E+05 |
|115.71|.98361E+04 | -.37722E+05 | -.37722E+05 |
|128.57|.43731E+04 | -.39685E+05 | -.32816E+05 |
|141.43|.32616E+04 | -.31533E+05 | -.31533E+05 |
|154.29|.57193E+04 | -.31373E+05 |.20519E+05 |
|167.14|.25226E+05 |.20612E+05 |.20612E+05 |
|180.00|.33954E+05 | -.28748E+04 | -.30479E+04 |
|192.86|.32957E+05 | -.23184E+05 | -.23184E+05 |
|205.71|.27637E+05 | -.35398E+05 | -.35398E+05 |
|218.57|.21440E+05 | -.40371E+05 | -.40371E+05 |
|231.43|.16276E+05 | -.39685E+05 | -.32816E+05 |
|244.29|.14866E+05 | -.28884E+05 | -.28884E+05 |
|257.14|.16443E+05 | -.26209E+05 |.25683E+05 |
|270.00|.34532E+05 |.28033E+05 |.28033E+05 |
|282.86|.41376E+05 |.64309E+04 |.62578E+04 |
|295.71|.38121E+05 | -.12460E+05 | -.12460E+05 |
|308.57|.30286E+05 | -.23794E+05 | -.23794E+05 |
|321.43|.21440E+05 | -.28468E+05 | -.28468E+05 |
|334.29|.13627E+05 | -.28081E+05 | -.21212E+05 |
|347.14|.97015E+04 | -.18160E+05 | -.18160E+05 |
|360.00|.90220E+04 | -.16903E+05 |.34989E+05 |
|372.86|.25226E+05 |.35454E+05 |.35454E+05 |
|385.71|.30652E+05 |.11595E+05 |.11422E+05 |
|398.57|.26517E+05 | -.98114E+04 | -.98114E+04 |
|411.43|.18383E+05 | -.23794E+05 | -.23794E+05 |
|424.29|.98361E+04 | -.31117E+05 | -.31117E+05 |
|437.14|.29033E+04 | -.33245E+05 | -.26376E+05 |
|450.00|.39568E+03 | -.25581E+05 | -.25581E+05 |
|462.86|.16009E+04 | -.26209E+05 |.25683E+05 |
|475.71|.20062E+05 |.24731E+05 |.24731E+05 |
|488.57|.28003E+05 | -.87905E+01 | -.18186E+03 |
|501.43|.26517E+05 | -.21714E+05 | -.21714E+05 |
|514.29|.21032E+05 | -.35398E+05 | -.35398E+05 |
|527.14|.15000E+05 | -.41840E+05 | -.41840E+05 |
|540.00|.10324E+05 | -.42551E+05 | -.35682E+05 |
|552.86|.97013E+04 | -.33002E+05 | -.33002E+05 |
|565.71|.12325E+05 | -.31373E+05 |.20519E+05 |
|578.57|.31666E+05 |.22082E+05 |.22082E+05 |
|591.43|.39906E+05 | -.89038E+01 | -.18198E+03 |
|604.29|.38121E+05 | -.19065E+05 | -.19065E+05 |
|617.14|.31756E+05 | -.30234E+05 | -.30234E+05 |
|630.00|.24306E+05 | -.34419E+05 | -.34419E+05 |
|642.86|.17745E+05 | -.33245E+05 | -.26376E+05 |
|655.71|.14866E+05 | -.22279E+05 | -.22279E+05 |
|668.57|.14973E+05 | -.19769E+05 |.32123E+05 |
|681.43|.31666E+05 |.33985E+05 |.33985E+05 |
|694.29|.37257E+05 |.11595E+05 |.11422E+05 |
|707.14|.32957E+05 | -.83416E+04 | -.83416E+04 |
|720.00|.24335E+05 | -.20928E+05 | -.20928E+05 |
Таблица 4 – Результаты расчета давлений и сил.
Такт впуска
-------------------------------------------------------------------------------------
| Угол |Давлен. Р | Сила PR |Сила ин. F|Сум.силаPS| Сила NS |Окp.сила T|Pад.сила Z|
-------------------------------------------------------------------------------------
|.00|.0000E+00|.0000E+00|-.1295E+05|-.1295E+05|.0000E+00|.0000E+00|-.1295E+05|
| 12.86|.0000E+00|.0000E+00|-.1242E+05|-.1242E+05|-.7559E+03|-.3501E+04|-.1194E+05|
| 25.71|.0000E+00|.0000E+00|-.1090E+05|-.1090E+05|-.1300E+04|-.5900E+04|-.9254E+04|
| 38.57|.0000E+00|.0000E+00|-.8572E+04|-.8572E+04|-.1481E+04|-.6502E+04|-.5779E+04|
| 51.43|.0000E+00|.0000E+00|-.5725E+04|-.5725E+04|-.1251E+04|-.5256E+04|-.2592E+04|
| 64.29|.0000E+00|.0000E+00|-.2682E+04|-.2682E+04|-.6807E+03|-.2712E+04|-.5506E+03|
| 77.14|.0000E+00|.0000E+00|.2385E+03|.2385E+03|.6585E+02|.2472E+03|-.1113E+02|
| 90.00|.0000E+00|.0000E+00|.2777E+04|.2777E+04|.7882E+03|.2777E+04|-.7882E+03|
|102.86|.0000E+00|.0000E+00|.4766E+04|.4766E+04|.1316E+04|.4354E+04|-.2344E+04|
|115.71|.0000E+00|.0000E+00|.6146E+04|.6146E+04|.1560E+04|.4860E+04|-.4072E+04|
|128.57|.0000E+00|.0000E+00|.6961E+04|.6961E+04|.1521E+04|.4494E+04|-.5529E+04|
|141.43|.0000E+00|.0000E+00|.7336E+04|.7336E+04|.1267E+04|.3583E+04|-.6526E+04|
|154.29|.0000E+00|.0000E+00|.7434E+04|.7434E+04|.8868E+03|.2427E+04|-.7083E+04|
|167.14|.0000E+00|.0000E+00|.7416E+04|.7416E+04|.4514E+03|.1210E+04|-.7331E+04|
|180.00|.0000E+00|.0000E+00|.7396E+04|.7396E+04|.4638E-02|.1170E-01|-.7396E+04|
-------------------------------------------------------------------------------------
Такт сжатия
-------------------------------------------------------------------------------------
| Угол |Давлен. Р | Сила PR |Сила ин. F|Сум.силаPS| Сила NS |Окp.сила T|Pад.сила Z|
-------------------------------------------------------------------------------------
|180.00|.8927E+05|.1731E+03|.7396E+04|.7569E+04|.5239E-02|.1378E-01|-.7569E+04|
|192.86|.9021E+05|.1897E+03|.7416E+04|.7606E+04|-.4629E+03|-.1241E+04|-.7518E+04|
|205.71|.9315E+05|.2416E+03|.7434E+04|.7676E+04|-.9157E+03|-.2505E+04|-.7313E+04|
|218.57|.9843E+05|.3351E+03|.7336E+04|.7671E+04|-.1325E+04|-.3747E+04|-.6824E+04|
|231.43|.1067E+06|.4817E+03|.6961E+04|.7443E+04|-.1626E+04|-.4805E+04|-.5912E+04|
|244.29|.1192E+06|.7014E+03|.6146E+04|.6847E+04|-.1738E+04|-.5415E+04|-.4536E+04|
|257.14|.1375E+06|.1026E+04|.4766E+04|.5792E+04|-.1599E+04|-.5291E+04|-.2848E+04|
|270.00|.1649E+06|.1510E+04|.2777E+04|.4287E+04|-.1217E+04|-.4287E+04|-.1217E+04|
|282.86|.2063E+06|.2241E+04|.2386E+03|.2480E+04|-.6847E+03|-.2570E+04|-.1157E+03|
|295.71|.2702E+06|.3371E+04|-.2682E+04|.6883E+03|-.1747E+03|-.6960E+03|.1413E+03|
|308.57|.3705E+06|.5143E+04|-.5725E+04|-.5817E+03|.1271E+03|.5340E+03|-.2633E+03|
|321.43|.5265E+06|.7900E+04|-.8572E+04|-.6723E+03|.1161E+03|.5100E+03|-.4532E+03|
|334.29|.7503E+06|.1185E+05|-.1090E+05|.9563E+03|-.1141E+03|-.5177E+03|.8121E+03|
|347.14|.9975E+06|.1622E+05|-.1242E+05|.3803E+04|-.2314E+03|-.1072E+04|.3656E+04|
|360.00|.1117E+07|.1834E+05|-.1295E+05|.5387E+04|-.1026E-01|-.4786E-01|.5387E+04|
Такт сгорания
-------------------------------------------------------------------------------------
| Угол |Давлен. Р | Сила PR |Сила ин. F|Сум.силаPS| Сила NS |Окp.сила T|Pад.сила Z|
-------------------------------------------------------------------------------------
|360.00|.4054E+07|.7023E+05|-.1295E+05|.5728E+05|-.7929E-01|-.3724E+00|.5728E+05|
|372.86|.4298E+07|.7454E+05|-.1242E+05|.6212E+05|.3781E+04|.1751E+05|.5972E+05|
|385.71|.3308E+07|.5706E+05|-.1090E+05|.4616E+05|.5507E+04|.2499E+05|.3920E+05|
|398.57|.2390E+07|.4082E+05|-.8572E+04|.3225E+05|.5571E+04|.2446E+05|.2174E+05|
|411.43|.1731E+07|.2918E+05|-.5725E+04|.2345E+05|.5124E+04|.2153E+05|.1062E+05|
|424.29|.1295E+07|.2148E+05|-.2683E+04|.1880E+05|.4770E+04|.1900E+05|.3858E+04|
|437.14|.1011E+07|.1645E+05|.2384E+03|.1669E+05|.4609E+04|.1730E+05|-.7789E+03|
|450.00|.8227E+06|.1313E+05|.2777E+04|.1591E+05|.4515E+04|.1591E+05|-.4515E+04|
|462.86|.6964E+06|.1090E+05|.4766E+04|.1567E+05|.4326E+04|.1431E+05|-.7704E+04|
|475.71|.6104E+06|.9383E+04|.6146E+04|.1553E+05|.3941E+04|.1228E+05|-.1029E+05|
|488.57|.5517E+06|.8345E+04|.6961E+04|.1531E+05|.3344E+04|.9882E+04|-.1216E+05|
|501.43|.5122E+06|.7646E+04|.7336E+04|.1498E+05|.2588E+04|.7318E+04|-.1333E+05|
|514.29|.4868E+06|.7199E+04|.7434E+04|.1463E+05|.1746E+04|.4776E+04|-.1394E+05|
|527.14|.4727E+06|.6949E+04|.7416E+04|.1437E+05|.8743E+03|.2344E+04|-.1420E+05|
|540.00|.4682E+06|.6869E+04|.7396E+04|.1427E+05|.2962E-01|.8129E-01|-.1427E+05|
-------------------------------------------------------------------------------------
Такт выхлопа
-------------------------------------------------------------------------------------
| Угол |Давлен. Р | Сила PR |Сила ин. F|Сум.силаPS| Сила NS |Окp.сила T|Pад.сила Z|
-------------------------------------------------------------------------------------
|540.00|.0000E+00|.0000E+00|.7396E+04|.7396E+04|.1536E-01|.4214E-01|-.7396E+04|
|552.86|.0000E+00|.0000E+00|.7416E+04|.7416E+04|-.4513E+03|-.1210E+04|-.7331E+04|
|565.71|.0000E+00|.0000E+00|.7434E+04|.7434E+04|-.8868E+03|-.2427E+04|-.7083E+04|
|578.57|.0000E+00|.0000E+00|.7336E+04|.7336E+04|-.1267E+04|-.3583E+04|-.6526E+04|
|591.43|.0000E+00|.0000E+00|.6961E+04|.6961E+04|-.1521E+04|-.4494E+04|-.5529E+04|
|604.29|.0000E+00|.0000E+00|.6146E+04|.6146E+04|-.1560E+04|-.4860E+04|-.4072E+04|
|617.14|.0000E+00|.0000E+00|.4766E+04|.4766E+04|-.1316E+04|-.4354E+04|-.2344E+04|
|630.00|.0000E+00|.0000E+00|.2777E+04|.2777E+04|-.7882E+03|-.2777E+04|-.7882E+03|
|642.86|.0000E+00|.0000E+00|.2386E+03|.2386E+03|-.6588E+02|-.2473E+03|-.1114E+02|
|655.71|.0000E+00|.0000E+00|-.2682E+04|-.2682E+04|.6807E+03|.2712E+04|-.5505E+03|
|668.57|.0000E+00|.0000E+00|-.5725E+04|-.5725E+04|.1251E+04|.5256E+04|-.2592E+04|
|681.43|.0000E+00|.0000E+00|-.8572E+04|-.8572E+04|.1481E+04|.6502E+04|-.5779E+04|
|694.29|.0000E+00|.0000E+00|-.1090E+05|-.1090E+05|.1300E+04|.5900E+04|-.9254E+04|
|707.14|.0000E+00|.0000E+00|-.1242E+05|-.1242E+05|.7560E+03|.3501E+04|-.1194E+05|
|720.00|.0000E+00|.0000E+00|-.1295E+05|-.1295E+05|.2237E-01|.1066E+00|-.1295E+05|
-------------------------------------------------------------------------------------
3. Уравновешивание двигателя
Силы инерции вращательно движущихся масс в однорядной звезде как и в одноцилиндровом двигателе, неуравновешенны и уравновешиваются противовесами:
![]() ,
,
где:
- центробежная сила вращающихся частей равна: ![]()
- сила инерции от неуравновешенных частей равна:
![]()
Тогда получим, что
![]()
Рассмотрим вопрос уравновешивания сил инерции поступательно движущихся масс.
Если исходить из положения, что все шатуны в двигателе центральные, то силы ![]() и
и ![]() всех цилиндров соответственно равны. В этом случае результирующая сила инерции первого порядка
всех цилиндров соответственно равны. В этом случае результирующая сила инерции первого порядка ![]() будет представлять собой постоянный по величине вектор, приложенный к шатунной шейке коленчатого вала и вращающийся вместе с коленом. Он равен
будет представлять собой постоянный по величине вектор, приложенный к шатунной шейке коленчатого вала и вращающийся вместе с коленом. Он равен
![]()
![]() ,
,
где ![]() - поступательно движущаяся масса, относящаяся к одному цилиндру,
- поступательно движущаяся масса, относящаяся к одному цилиндру, ![]() ;
;
Z – число цилиндров в одной звезде.
Тогда ![]() . - боковой цилиндр.
. - боковой цилиндр.
Такую силу легко уравновесить, добавив к противовесам соответствующую массу.
Результирующий вектор сил инерции второго порядка равен нулю, т.е. по силам ![]() самоуравновешивание обеспечивается.
самоуравновешивание обеспечивается.
В действительности же вследствие разницы в массах шатунов и в кинематике поршней главного и боковых цилиндров результирующий вектор сил инерции первого порядка не постоянный по величине, а содержит переменную составляющую; конец вектора описывает эллипс, большая ось которого совпадает с направлением оси главного цилиндра. Амплитуда переменной составляющей
![]() ,
,
где ![]() - разность поступательно движущихся масс главного и бокового цилиндра:
- разность поступательно движущихся масс главного и бокового цилиндра: ![]() ,
,
Тогда в момент ![]()
![]() равна:
равна:
![]()
Рисунок 5 – Результирующий вектор сил инерции первого порядка.
4. Расчет на прочность коленчатого вала
Коленчатый вал служит для преобразования возвратно-поступательного движения поршней в цилиндрах двигателя во вращательное движение и для преобразования силы давления газов на поршни – в крутящий момент.
Коленчатый вал воспринимает всю избыточную мощность, развиваемую газами в цилиндрах, и передает ее на винт, который является основным потребителем мощности двигателя, на нагнетатель, механизм газораспределения, агрегаты.
4.1 Силы, действующие на колено коленчатого вала
При работе двигателя колено вала нагружается следующими силами (рисунок 6)
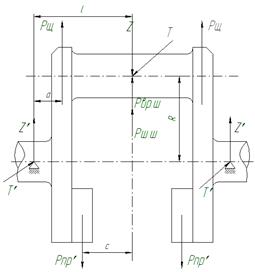
Рисунок 6 – Силовое нагружение колена
1) В плоскости колена действует сила Z
2) Перпендикулярно к плоскости колена действует сила Т
3) В плоскости колена действует сила инерции от вращающихся масс шатуна:
![]() ;
; ![]() ;
;
![]() , (смотри рисунок 7)
, (смотри рисунок 7)
где ![]()
![]()
![]()
Тогда ![]()
![]()
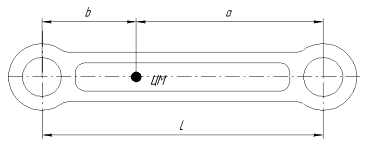
Рисунок 7 – Разнос масс шатуна
4) В плоскости колена действует сила инерции от массы шатунной шейки ![]()
![]()
(Все необходимые объемы соответствующих частей деталей и радиусы их центров масс определены по твердотельной модели исполненной в пакете Solid Works)
5) В плоскости колена действуют силы инерции от масс щек ![]() .
.
![]()
6) В плоскости колена действуют силы инерции противовесов РПР.
![]()
7) От сил, действующих в плоскости колена, на опорах колена возникают реакции ![]() . В случае симметричного колена
. В случае симметричного колена
![]() .
.
![]()
8) От силы ![]() на опорах колена возникают реакции
на опорах колена возникают реакции ![]() , действующие перпендикулярно к плоскости колена. В случае симметричного колена
, действующие перпендикулярно к плоскости колена. В случае симметричного колена ![]() .
.
Силы Т, Z, реакции ![]() и
и ![]() переменны по величине и направлению и меняются в зависимости от угла поворота колена. Расчет этих сил реакции приведен в таблице 5.
переменны по величине и направлению и меняются в зависимости от угла поворота колена. Расчет этих сил реакции приведен в таблице 5.
4.2 Определение запаса прочности в шатунной шейке
Напряжения в расчетном сечении шатунной шейки при любом положении кривошипа можно определить, если колено рассматривать, как разрезную двухопорную балку. Это значит, что каждое колено мысленно вырезается двумя сечениями, проходящими через середины коренных подшипников, и рассматривается как балка на двух опорах (рисунок 8)
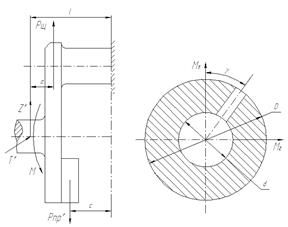
Рисунок 8 – Расчетная модель шатунной шейки
Очевидно, что наиболее напряженным сечением шатунной шейки будет сечение, лежащее посередине шейки.
Разрезаем шатунную шейку посередине, отбрасываем правую часть, закрепляем левую часть по расчетному сечению и определяем напряжения от оставшихся сил и моментов, включая и силы реакций опор:
а) от сил, действующих в плоскости колена, расчетное сечение нагружается изгибающим моментом:
![]() ;
;
б) от сил, действующих в плоскости, перпендикулярной к плоскости колена, расчетное сечение нагружается изгибающим моментом:
![]()
Рисунок 7 – Твердотельная модель коленчатого вала (фрагмент)
Опасные точки шатунной шейки расположены у масляного отверстия (смотри рисунок 7.). Если его ось составляет с плоскостью колена угол g (g=300, так как при этом положении силы Т и Z минимальны), то изгибающий момент в плоскости, проходящей через ось масляного отверстия, равен:
![]()
Знак “-” показывает, что момент ![]() вызывает у края отверстия напряжения сжатия.
вызывает у края отверстия напряжения сжатия.
Таблица 5 – Результаты расчета
| T,Н | Z,Н | My |
||||||||||||||||||
| 0 | 0 | -2950 | 0 | 21119 | 395 | 0 | 197 | 15 | 0 | 0 | ||||||||||
| 12,86 | -3501 | -11940 | -1751 | 21624 | 400 | -228 | 3 | 0 | -133 | -5 | ||||||||||
| 25,71 | -5900 | -9254 | -2950 | 22967 | 413 | -384 | -125 | -9 | -224 | -8 | ||||||||||
| 38,57 | -6502 | -5779 | -3251 | 24705 | 431 | -423 | -151 | -11 | -247 | -9 | ||||||||||
| 51,43 | -5256 | -2592 | -2628 | 26298 | 447 | -342 | -73 | -5 | -199 | -7 | ||||||||||
| 64,29 | -2712 | -551 | -1356 | 27319 | 457 | -176 | 76 | 6 | -103 | -4 | ||||||||||
| 77,14 | 247 | -11 | 124 | 27588 | 460 | 16 | 244 | 18 | 9 | 0 | ||||||||||
| 90,00 | 2777 | -788 | 1389 | 27200 | 456 | 181 | 384 | 28 | 105 | 4 | ||||||||||
| 102,86 | 4354 | -2344 | 2177 | 26422 | 448 | 283 | 469 | 35 | 165 | 6 | ||||||||||
| 115,71 | 4860 | -4072 | 2430 | 25558 | 439 | 316 | 493 | 37 | 184 | 7 | ||||||||||
| 128,57 | 4494 | -5529 | 2247 | 24830 | 432 | 292 | 469 | 35 | 171 | 6 | ||||||||||
| 141,43 | 3583 | -6526 | 1792 | 24331 | 427 | 233 | 415 | 31 | 136 | 5 | ||||||||||
| 154,29 | 2427 | -7083 | 1214 | 24053 | 424 | 158 | 349 | 26 | 92 | 3 | ||||||||||
| 167,14 | 1210 | -7331 | 605 | 23929 | 423 | 79 | 280 | 21 | 46 | 2 | ||||||||||
| 180,00 | 0 | -7396 | 0 | 23896 | 423 | 0 | 211 | 16 | 0 | 0 | ||||||||||
| 180,00 | 0 | -7569 | 0 | 23810 | 422 | 0 | 211 | 16 | 0 | 0 | ||||||||||
| 192,86 | -1241 | -7518 | -621 | 23835 | 422 | -81 | 141 | 10 | -47 | -2 | ||||||||||
| 205,71 | -2505 | -7313 | -1253 | 23938 | 423 | -163 | 70 | 5 | -95 | -4 | ||||||||||
| 218,57 | -3747 | -6824 | -1874 | 24182 | 425 | -244 | 2 | 0 | -142 | -5 | ||||||||||
| 231,43 | -4805 | -5912 | -2403 | 24638 | 430 | -312 | -55 | -4 | -182 | -7 | ||||||||||
| 244,29 | -5415 | -4536 | -2708 | 25326 | 437 | -352 | -86 | -6 | -205 | -8 | ||||||||||
| 257,14 | -5291 | -2848 | -2646 | 26170 | 445 | -344 | -75 | -6 | -201 | -7 | ||||||||||
| 270,00 | -4287 | -1217 | -2144 | 26986 | 453 | -279 | -15 | -1 | -163 | -6 | ||||||||||
| 282,86 | -2570 | -116 | -1285 | 27536 | 459 | -167 | 85 | 6 | -98 | -4 | ||||||||||
| 295,71 | -696 | 141 | -348 | 27665 | 460 | -45 | 191 | 14 | -26 | -1 | ||||||||||
| 308,57 | 534 | -263 | 267 | 27462 | 458 | 35 | 259 | 19 | 20 | 1 | ||||||||||
| 321,43 | 510 | -453 | 255 | 27367 | 457 | 33 | 257 | 19 | 19 | 1 | ||||||||||
| 334,29 | -518 | 812 | -259 | 28000 | 464 | -34 | 203 | 15 | -20 | -1 | ||||||||||
| 347,14 | -1072 | 3656 | -536 | 29422 | 478 | -70 | 179 | 13 | -41 | -2 | ||||||||||
| 360,00 | 0 | 5387 | 0 | 30288 | 486 | 0 | 243 | 18 | 0 | 0 | ||||||||||
| 360,00 | 0 | 57280 | 0 | 56234 | 746 | 0 | 373 | 28 | 0 | 0 | ||||||||||
| 372,86 | 17510 | 59720 | 8755 | 57454 | 758 | 1138 | 1365 | 101 | 665 | 25 | ||||||||||
| 385,71 | 24990 | 39200 | 12495 | 47194 | 656 | 1624 | 1734 | 128 | 948 | 35 | ||||||||||
| 398,57 | 24460 | 21740 | 12230 | 38464 | 568 | 1590 | 1661 | 123 | 928 | 34 | ||||||||||
| 411,43 | 21530 | 10620 | 10765 | 32904 | 513 | 1399 | 1468 | 109 | 817 | 30 | ||||||||||
| 424,29 | 19000 | 3858 | 9500 | 29523 | 479 | 1235 | 1309 | 97 | 721 | 27 | ||||||||||
| 437,14 | 17300 | -779 | 8650 | 27205 | 456 | 1125 | 1202 | 89 | 657 | 24 | ||||||||||
| 450,00 | 15910 | -4515 | 7955 | 25337 | 437 | 1034 | 1114 | 83 | 604 | 22 | ||||||||||
| 462,86 | 14310 | -7704 | 7155 | 23742 | 421 | 930 | 1016 | 75 | 543 | 20 | ||||||||||
| 475,71 | 12280 | -10290 | 6140 | 22449 | 408 | 798 | 895 | 66 | 466 | 17 | ||||||||||
| 488,57 | 9882 | -12160 | 4941 | 21514 | 399 | 642 | 756 | 56 | 375 | 14 | ||||||||||
| 501,43 | 7318 | -13330 | 3659 | 20929 | 393 | 476 | 608 | 45 | 278 | 10 | ||||||||||
| 514,29 | 4776 | -13940 | 2388 | 20624 | 390 | 310 | 464 | 34 | 181 | 7 | ||||||||||
| 527,14 | 2344 | -14200 | 1172 | 20494 | 389 | 152 | 326 | 24 | 89 | 3 | ||||||||||
| 540,00 | 0 | -14270 | 0 | 20459 | 388 | 0 | 194 | 14 | 0 | 0 | ||||||||||
| 540,00 | 0 | -7396 | 0 | 23896 | 423 | 0 | 211 | 16 | 0 | 0 | ||||||||||
| 552,86 | -1210 | -7331 | -605 | 23929 | 423 | -79 | 143 | 11 | -46 | -2 | ||||||||||
| 565,71 | -2427 | -7083 | -1214 | 24053 | 424 | -158 | 75 | 6 | -92 | -3 | ||||||||||
| 578,57 | -3583 | -6526 | -1792 | 24331 | 427 | -233 | 12 | 1 | -136 | -5 | ||||||||||
| 591,43 | -4494 | -5529 | -2247 | 24830 | 432 | -292 | -37 | -3 | -171 | -6 | ||||||||||
| 604,29 | -4860 | -4072 | -2430 | 25558 | 439 | -316 | -54 | -4 | -184 | -7 | ||||||||||
| 617,14 | -4354 | -2344 | -2177 | 26422 | 448 | -283 | -21 | -2 | -165 | -6 | ||||||||||
| 630,00 | -2777 | -788 | -1389 | 27200 | 456 | -181 | 71 | 5 | -105 | -4 | ||||||||||
| 642,86 | -247 | -11 | -124 | 27588 | 460 | -16 | 216 | 16 | -9 | 0 | ||||||||||
| 655,71 | 2712 | -551 | 1356 | 27319 | 457 | 176 | 381 | 28 | 103 | 4 | ||||||||||
| 668,57 | 5256 | -2592 | 2628 | 26298 | 447 | 342 | 519 | 38 | 199 | 7 | ||||||||||
| 681,43 | 6502 | -5779 | 3251 | 24705 | 431 | 423 | 581 | 43 | 247 | 9 | ||||||||||
| 694,29 | 5900 | -9254 | 2950 | 22967 | 413 | 384 | 539 | 40 | 224 | 8 | ||||||||||
| 707,14 | 3501 | -11940 | 1751 | 21624 | 400 | 228 | 397 | 29 | 133 | 5 | ||||||||||
| 720,00 | 0 | -12950 | 0 | 21119 | 395 | 0 | 197 | 15 | 0 | 0 | ||||||||||
Определив изгибающий момент в опасной точке сечения, легко вычислить напряжение в этой точке:
![]() ,
,
где ![]() - момент сопротивления изгибу.
- момент сопротивления изгибу.
Касательные напряжения от скручивающего момента
![]() ,
,
где ![]() ,
,
![]() .
.
Амплитудные напряжения циклов:
![]() ;
;
![]() .
.
Зная предел усталости материала вала, определим запас прочности по нормальным и касательным напряжениям:
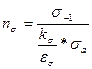 ,
, 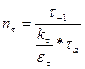 ,
,
где ![]() - коэффициент, учитывающий влияние концентрации напряжений при переменных нормальных напряжениях;
- коэффициент, учитывающий влияние концентрации напряжений при переменных нормальных напряжениях;
![]() - коэффициент, учитывающий влияние размеров детали при переменных нормальных напряжениях;
- коэффициент, учитывающий влияние размеров детали при переменных нормальных напряжениях;
![]() - коэффициент, учитывающий влияние концентрации напряжений при переменных касательных напряжениях;
- коэффициент, учитывающий влияние концентрации напряжений при переменных касательных напряжениях;
![]() - коэффициент, учитывающий влияние размеров детали при переменных касательных напряжениях.
- коэффициент, учитывающий влияние размеров детали при переменных касательных напряжениях.
Для шеек валов у края смазочных отверстий ![]()
![]() .
.
Тогда
![]() ,
, ![]()
Суммарный запас прочности
![]()
Таким образом, необходимый запас прочности по нормальным и касательным напряжениям для шатунной шейки обеспечивается.
4.3 Определение запаса прочности в коренной шейке
В коренной шейке определяются только касательные напряжения от действия крутящего момента ![]() .
.
Касательные напряжения от скручивающего момента ![]() , где
, где
![]()
Величина крутящего момента и касательных напряжений приведены в таблице 6.
Таблица 6 – Величина крутящего момента и касательных напряжений
| 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
| -66,5 | -1,1 | -23,6 | -0,4 | 332,7 | 5,7 | -23,0 | -0,4 |
| -112,1 | -1,9 | -47,6 | -0,8 | 474,8 | 8,1 | -46,1 | -0,8 |
| -123,5 | -2,1 | -71,2 | -1,2 | 464,7 | 7,9 | -68,1 | -1,2 |
| -99,9 | -1,7 | -91,3 | -1,6 | 409,1 | 7,0 | -85,4 | -1,5 |
| -51,5 | -0,9 | -102,9 | -1,8 | 361,0 | 6,2 | -92,3 | -1,6 |
| 4,7 | 0,1 | -100,5 | -1,7 | 328,7 | 5,6 | -82,7 | -1,4 |
| 52,8 | 0,9 | -81,5 | -1,4 | 302,3 | 5,2 | -52,8 | -0,9 |
| 82,7 | 1,4 | -48,8 | -0,8 | 271,9 | 4,6 | -4,7 | -0,1 |
| 92,3 | 1,6 | -13,2 | -0,2 | 233,3 | 4,0 | 51,5 | 0,9 |
| 85,4 | 1,5 | 10,1 | 0,2 | 187,8 | 3,2 | 99,9 | 1,7 |
| 68,1 | 1,2 | 9,7 | 0,2 | 139,0 | 2,4 | 123,5 | 2,1 |
| 46,1 | 0,8 | -9,8 | -0,2 | 90,7 | 1,5 | 112,1 | 1,9 |
| 23,0 | 0,4 | -20,4 | -0,3 | 44,5 | 0,8 | 66,5 | 1,1 |
| 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 |
Зная предел усталости материала вала, определим запас прочности по касательным напряжениям:;
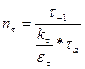 ,
,
где:
![]() ,
,
![]()
Таким образом, запас прочности по касательным напряжениям для коренной шейки обеспечивается.
5. Расчет поршневого пальца
Расчет производится на прочность от изгибающих моментов; на предельно допустимую деформацию (овализацию) во избежание заклинивания в верхней головке шатуна; на удельное давление на его трущихся поверхностях.
Рисунок 8 – Модель поршневого пальца
При плавающем пальце для каждой точки его расчетного сечения возможен такой случай, когда в момент действия максимального усилия (таковым обычно является ![]() ) она окажется либо в зоне максимально растянутых, либо в зоне максимально сжатых волокон. Таким образом, в каждой точке расчетного сечения напряжение может колебаться в соответствии с изменением нагрузки от
) она окажется либо в зоне максимально растянутых, либо в зоне максимально сжатых волокон. Таким образом, в каждой точке расчетного сечения напряжение может колебаться в соответствии с изменением нагрузки от ![]() до
до ![]() , где
, где ![]() .
.
Рисунок 9 – Схема нагружения поршневого пальца
Этот случай симметричного цикла нагружения опасен с точки зрения прочности поршневого пальца и поэтому является расчетным.
Изгибающий момент
![]()
(где L – расстояние между серединами опорных участков в бобышках поршня, м; а – длина верхней головки шатуна, м; Рс
– сила, действующая на палец со стороны поршня, Н, изменяем в пределах от ![]() до
до ![]() , где
, где
![]() , где
, где ![]()
Масса поршня
![]()
Значение ![]() в зависимости от угла поворота коленчатого вала приведены в таблица 7.
в зависимости от угла поворота коленчатого вала приведены в таблица 7.
Таблица 7 – Значение ![]() в зависимости от угла поворота коленчатого вала
в зависимости от угла поворота коленчатого вала
| 0,00 | -11831,50 | 51,43 | -5235,48 | 102,86 | 4348,29 | 154,29 | 6791,70 |
| 12,86 | -11347,48 | 64,29 | -2456,71 | 115,71 | 5609,74 | 167,14 | 6775,33 |
| 25,71 | -9958,18 | 77,14 | 209,64 | 128,57 | 6356,74 | 180,00 | 6756,88 |
| 38,57 | -7835,03 | 90,00 | 2529,91 | 141,43 | 6700,84 |
![]()
Тогда ![]()
Среднее напряжение рассматриваемого цикла равно нулю, а амплитуда цикла ![]() . Момент сопротивления пальца изгибу
. Момент сопротивления пальца изгибу
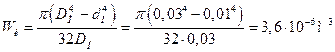 .
.
![]()
Запас прочности пальца на изгиб определяется по выражению
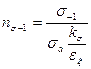 ,
,
где коэффициент фактора размерности ![]() для диаметра пальца 25мм составляет 0,92.
для диаметра пальца 25мм составляет 0,92.
![]() - коэффициент, учитывающий влияние концентрации напряжений (связанных с резким изменением поперечного сечения) при переменных нормальных напряжениях. Так как палец не имеет скачков поперечного сечения по всей своей длине, то принимаем
- коэффициент, учитывающий влияние концентрации напряжений (связанных с резким изменением поперечного сечения) при переменных нормальных напряжениях. Так как палец не имеет скачков поперечного сечения по всей своей длине, то принимаем ![]()
Величина ![]() составляет 450 МПа. Тогда
составляет 450 МПа. Тогда
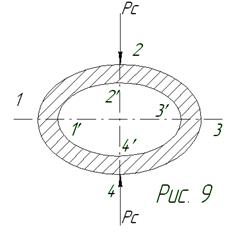
Рисунок 10 – Схема овализации поршневого пальца
Так как по этой формуле запас прочности поршневого пальца значительно занижен по сравнению с действительным запасом, то полученный запас прочности является достаточно надежным критерием оценки прочности.
Под действием силы РС
палец овализируется (рисунок 10). В направлении действия РС
диаметр пальца уменьшается, в противоположном направлении – увеличивается. Как показали исследования Р.С. Кинасошвили, наибольшие напряжения при овализации возникают в точках ![]() и
и ![]() и их величина
и их величина
![]() ,
,
где =f(), а , в свою очередь равна
![]() .
.
Графическая зависимость =f() приведена в пособии [4]. По ней определяем ![]() .
.
Тогда
![]()
Так как допустимое напряжение овализации лежит в пределах 230-270МПа [4], то запас прочности по овализации обеспечивается.
Степень овализацци задается обычно как увеличение внешнего диаметра в направлении, перпендикулярном приложению нагрузки. Это увеличение ![]() определим по формуле Кинасошвили [4]:
определим по формуле Кинасошвили [4]:
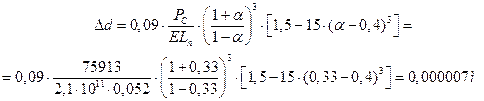
Полученная степень овализации не превышает допустимую (0,05мм), следовательно, условие незаклинивания в верхней головке шатуна соблюдается.
Удельное давление пальца на бобышки поршня:
![]() , где b – длина контактирующей с пальцем поверхности бобышки
, где b – длина контактирующей с пальцем поверхности бобышки
![]()
Тогда как допустимое удельное давление пальца на бобышки поршня составляет 50 МПа [4].
6. Расчет поршневых колец
При работе поршневое кольцо должно находиться в сжатом состоянии и создавать некоторое давление на стенки цилиндра. Величина этого давления зависит как от упругой деформации кольца, сжатого в цилиндре, так и от размеров сечения кольца.
Если принять, что средний радиус кольца в свободном состоянии равен радиусу наружной поверхности поршня (рисунок 10), то формула
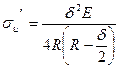
с учетом того, что ![]()
![]() обычно в 20-25 раз меньше R принимает вид
обычно в 20-25 раз меньше R принимает вид
![]() .
.
Для чугунных колец Е=82500МПа. Тогда
![]()
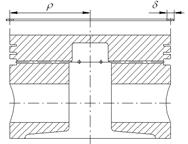
Рисунок 10 – Схема расположения и геометрические размеры кольца
Допускаемые напряжения сжатия составляют 135-150МПа, поэтому запас прочности по напряжениям сжатия удовлетворяет требованиям прочности.
Расчет поршневого кольца сделан в предположении равномерного давления кольца на стенку цилиндра. Однако теоретическое и экспериментальное изучение условий работы кольца показало целесообразность изготовления кольца с неравномерной эпюрой давления по окружности. В частности, целесообразно увеличивать давление у замка.
Величина зазора в свободном состоянии
![]() . В частном случае при
. В частном случае при ![]()
![]()
7. Расчет прицепного шатуна
Производим расчет на устойчивость прицепного шатуна.
Определим осевой момент инерции сечения прицепного шатуна.
![]() ,
,
где ![]() - момент инерции прямоугольника, наиболее удаленного от оси х-х (рисунок 11)
- момент инерции прямоугольника, наиболее удаленного от оси х-х (рисунок 11)
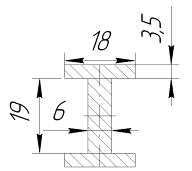
Рисунок 11 – Расчетная схема прицепного шатуна
![]()
![]()
![]()
Полная площадь поперечного сечения (площадь брутто) составляет ![]()
Минимальный радиус инерции
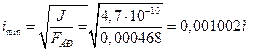
Гибкость ![]() , где n - коэффициент приведения длины, зависящий от способа заделки стержня. Рассматриваем прицепной шатун как стержень с шарнирно закрепленными концами, при этом способе n=0,7.
, где n - коэффициент приведения длины, зависящий от способа заделки стержня. Рассматриваем прицепной шатун как стержень с шарнирно закрепленными концами, при этом способе n=0,7.
Тогда ![]() .
.
Так как явление продольного изгиба существует не только в пределах упругости, но и за ними, то для определения критического напряжения нельзя пользоваться формулой Эйлера, так как она дает завышенные значения.
Теоретическое решение задачи об устойчивости за пределом пропорциональности сложно, поэтому обычно пользуются эмпирическими формулами, полученными в результате обработки большого количества опытных данных.
Определим критическое напряжение стержня по формуле Ф.С. Ясинского: ![]() , значения эмпирических коэффициентов a и b определяем по таблицам [5]:
, значения эмпирических коэффициентов a и b определяем по таблицам [5]:![]() ,
,![]() . Тогда
. Тогда
![]()
Действующее максимальное напряжение в сечении шатуна ![]() ,
,
![]() .
.
Коэффициент запаса устойчивости:
![]()
8. Расчет поршня
Статический расчет твердотельной модели поршня, выполненный в пакете Solid Works, производим в пакете Cosmos Works.
В основу расчета заложен метод конечных элементов (МКЭ). Перед расчетом задаем материал поршня (алюминиевый сплав), условия закрепления по плоскостям и цилиндрическим поверхностям и производим разбиение твердотельной модели на сетку конечных элементов (рисунок 13). Далее производим расчет на статическую прочность.


Рисунок 13 – Результат расчета на статическую прочность
По результатам расчета видно, что максимальные напряжения, а следовательно и минимальные коэффициенты запаса, расположились у основания бобышек (с внутренней стороны поршня) и составляют 136,7МПа, а так же на проточках под поршневые кольца (95МПа) и на периферии маслоотводных отверстий (100МПа).
Максимальные деформации характерны для диаметрально-противоположных точек “дна” поршня, расположенных в плоскости, перпендикулярной к оси поршневого пальца и составляют ![]() м.
м.
Список использованной литературы
1 . И.П. Пелепейченко, Н.И. Кормилов “Тепловые двигатели”, - Харьков: ХАИ, 1977. – 108с.
2. И.П. Пелепейченко, В.И. Крирченко “Динамический расчет авиационного однорядного звездообразного двигателя на ЭВМ”, - Харьков: ХАИ, 1982. – 56с.
3. В.И. Крирченко “ Динамический расчет поршневого звездообразного двигателя”, - Харьков: ХАИ, 1973. – 68с.
4. Ю.А. Гусев, С.В. Епифанов, А.В. Белогуб “Поршни двигателей внутреннего сгорания”, - Харьков: ХАИ, 1999. – 32с.
5. Г.С. Писаренко, В.Г. Попков “Сопротивление материалов”, - Киев: Вища школа, 1986. – 776с.