Задачи на отношения Ханты-Мансийск Новосибирск

СОДЕРЖАНИЕ: Михеев Ю. В. Задачи на отношения. Учебно-методическое пособие. Ханты-Мансийск, 2004, 12 с

Югорский физико-математический лицей

Заочное отделение

Ю.В. Михеев

Задачи на отношения

Ханты-Мансийск - Новосибирск

2008


Михеев Ю.В. Задачи на отношения. Учебно-методическое пособие. Ханты-Мансийск, 2004, 12 с.

В пособии задании рассматриваются свойства медиан, высот и биссектрис треугольника и разнообразные примеры на применение этих свойств.

Рецензент к.ф.-м.н. В.П. Чуваков

Михеев Ю.В. 2004


Отношение величин возникают часто. Иногда требуется установить, во сколько раз одна величина больше или меньше другой величины, иногда известно отношение величин и нужно найти одну из них, зная значение другой, и т. д.

В геометрии задачами такого вида, в основном, являются задачи на отношение длин отрезков и кривых, на отношение площадей фигур, на отношение объемов.

Каждый раз при вычислении отношений величин нужно следить за тем, чтобы их значения были выражены в одинаковых единицах измерения. В дальнейшем для упрощения записи значения длин и площадей будем обозначать только числами, предполагая, что в реальной практической задаче всегда можно указать необходимые единицы измерения.

I . Отношения отрезков на прямой

При решении задач на отношение длин отрезков, расположенных на одной прямой, всегда используются основные свойства длины:

- длина каждого отрезка неотрицательна;

- длина отрезка BA равна длине отрезка AB ;

- равные отрезки имеют одинаковую длину;

- если отрезок AB составлен из отрезков AC и CB , то .

Из перечисленных свойств следует, что если отрезок составлен из нескольких равных частей, то длина всего отрезка равна длине одной части, умноженной на количество частей. С помощью этого свойства иногда отношение отрезков находится легко.

Пример 1. На отрезке AB точка C расположена так, что . Найти отношение .

Решение. Разобьем отрезок AC на 5 равных частей. Пусть длина каждой части равна a .

Рис. 1

Тогда , а из условия следует, что (рис. 1). Поэтому и .

Данный способ удалось применить потому, что по условию отношение отрезков равно отношению небольших натуральных чисел. В более сложных ситуациях аналогичные задачи удается решить алгебраическим способом.

Пример 2. На отрезке AB точка C расположена так, что

Рис. 2

. Найти отношение .

Решение . Пусть . Тогда из условия , откуда . Поэтому (рис. 2), откуда .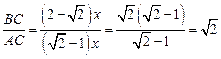

Когда на прямой заданы три или большее число точек, то по некоторым известным отношениям отрезков также можно находить отношения каких-то других отрезков.

Пример 3. На отрезке AB точки C и D расположены так, что точка C лежит между точками A и D (рис. 3).

Рис. 3

Известно, что ,. Найти отношение .

Решение. Пусть , . Тогда из условия , . Поэтому и . Следовательно, , и . Но тогда , откуда .

Геометрически решение данной задачи можно представить в очень наглядном виде. Однако сделать это сложнее, чем решить задачу алгебраическим способом. Чтобы придумать геометрическое решение, нужно понять, что отношение хорошо представить наглядно, когда отрезок AB разделен на равные части, число которых кратно трем, а отношение хорошо представляется наглядно – когда число равных частей кратно пяти.

Рис. 4

Так как число 15 кратно и 3, и 5, то поделив отрезок AB на 15 равных частей, точки C и D следует поставить так, как показано на рис. 4. В результате ответ, найденный в решении, становится очевидным.

II . Отношения отрезков на плоскости

При решении задач на вычисление отношений отрезков, не лежащих на одной прямой, чаще всего используются теорема Фалеса и подобие треугольников. Приступая к изучению данного раздела, следует вспомнить этот материал, и особенно теорему Фалеса, формулировку которой приводим в обобщенном виде.

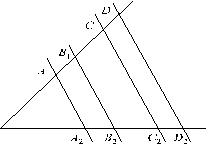
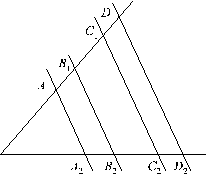
Пусть параллельные прямые a , b , c , d , и т. д. пересекают одну сторону заданного угла в точках A 1 , B 1 , C 1 , D 1 , и т. д., вторую сторону угла соответственно в точках A 2 , B 2 , C 2 , D 2 , и т. д. (рис. 5). Тогда , и т. д.

Рис. 5

В тех случаях, когда на чертеже имеются параллельные прямые, можно всегда пытаться применять теорему Фалеса.

Пример 4. В треугольнике ABC точка D лежит на стороне AC , а точки E на AB , H на BC , F и G на BD расположены так, что , , EF и GH параллельны AC . Найти отношение .

Решение. Заметим, что прямые AC и EF параллельны и пересекают стороны угла ABD (рис. 6).

Поэтому по теореме Фалеса . Аналогично, из того что параллельные прямые AC и GH пересекают стороны угла DBC , находим . В итоге на прямой BD становятся известными два отношения отрезков, и решение завершаем так, как рассматривалось в первом разделе.

Рис. 6

Пусть , .

Тогда , , , , откуда , , .

В некоторых задачах следует пытаться самим добавлять прямые так, чтобы получались либо параллельные секущие сторон угла, либо пары подобных треугольников.

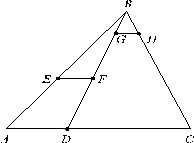
Пример 5. В треугольнике ABC точки D на стороне AC и E на стороне BC расположены так, что .

Рис. 7

Отрезки BD и AE пересекаются в точке P. Найти отношение .

Решение. С целью получения параллельных секущих сторон углов проведем через точку D прямую параллельно прямой AE , которая пересекает сторону BC в точке F (рис. 7). Так как AE и DF являются параллельными секущими сторон угла ACB , то . Поэтому , откуда , . Далее, из условия следует, что , откуда и , . Так как , то . После этого замечаем, что прямые DF и AE являются параллельными секущими сторон угла CBD , откуда .

Таким образом, добавление прямой DF позволяет свести задачу на вычисление отношения к задаче на вычисление отношения .

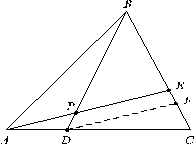
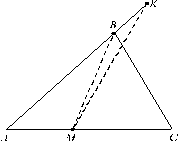
Пример 6. В треугольнике ABC точка M середина стороны AB , а точка K расположена на продолжении стороны AC так, что . Прямая MK пересекает сторону BC в точке P . Найти отношение .

Рис. 8

Решение. Добавив прямую CF, параллельную прямой MK (рис. 8), задачу на вычисление сводим к задаче на вычисление . Для сокращения записей обозначим длину стороны AB через a . Из условия . Далее, так как прямые CF и MK являются параллельными секущими сторон угла CAB , то , откуда .

Поэтому .

При вычислении отношений отрезков можно использовать и подобие треугольников.

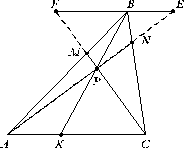
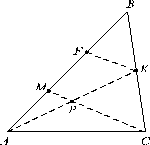
Пример 7. В треугольнике ABC точки M на стороне AB и N на стороне BC расположены так, что , . Отрезки AN и CM пересекаются в точке P , а прямая BP пересекает сторону AC в точке K . Найти отношение .

Рис. 9

Решение. С целью получения пар подобных треугольников проведем через вершину B прямую m параллельно прямой AC и отметим точки E и F пересечения прямой m с прямыми AN и BM (рис. 9). Далее последовательно обратим внимание на пары подобных треугольников. Прежде всего заметим, что подобны треугольники BMF и AMC , так как и . По свойству подобных треугольников получаем, что , откуда , и . Аналогично из подобия треугольников BNE и ANC находим, что . В результате . После этого следует обратить внимание на подобие треугольников PEF и PAC , откуда . Наконец, можно найти еще пары подобных треугольников, что позволяет получить в задаче ответ. Заметим, что треугольники BPE и APK подобны, откуда , , и .

III . Отношение площадей

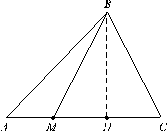
Рассмотрим треугольник ABC и выберем на стороне AC точку

M . Если провести в треугольнике ABC высоту BH , то эта высота одновременно будет и высотой в треугольнике ABM (рис. 10). Записывая площади треугольников ABC и ABM , получаем

Рис. 10

, ,

и .

Следовательно, зная площадь треугольника ABC и отношение , можно очень быстро вычислить площадь треугольника AMC .

Заметим, что найденная закономерность сохраняется и в том случае, когда точка M находится на продолжении стороны AC . Снова рассмотрим треугольник ABC , и на сторонах AC и AB , либо на продолжениях этих сторон, выберем соответственно точки M и K (рис. 11).

Рис. 11

Используя найденную закономерность получаем, что

и .

Отсюда .

Пример 8. В треугольнике ABC точки M на стороне AB и K на стороне BC расположены так, что , . Отрезки AK и CM пересекаются в точке P. Найти площадь четырехугольника PMBK, если площадь треугольника ABC равна 12.

Решение. Сначала вычислим отношение , для чего проведем (рис. 12). Так как , то , а из того, что , , получаем, откуда и . Теперь переходим к вычислению площадей.

Так как , то .

Далее,

Рис. 12

.

Поэтому .

Рассмотренную закономерность можно обобщить следующим образом: если для треугольников ABC и EFG известны отношения двух сторон и отношение соответствующих высот, то .

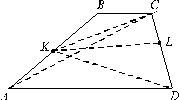
Пример 9. В трапеции ABCD основание AD в три раза больше основания BC . На боковых сторонах AB и CD поставлены точки K и L соответственно так, что . Найти отношение площадей AKLD и KBCL .

Решение. Обозначим площадь треугольника ABC через P . Так как высоты треугольников ABC и ADC равны и , то , и площадь трапеции равна 4P . Далее, треугольники ABD и ACD имеют общее основание AD и равные высоты,

Рис. 13

поэтому . Так как , то . Аналогично, . Следовательно, .

Так как , то . Поэтому

. После этого получаем и .

В качестве еще одного примера на применение рассмотренных свойств разберем одну известную олимпиадную задачу.

Пример 10. На продолжениях сторон AB , BC , CD , DA четырехугольника ABCD соответственно строятся точки M , N , K , L так, что , , , . Доказать, что площадь четырехугольника MNKL в пять раз больше площади четырехугольника ABCD .

Решение. Сделаем чертеж (рис. 14) и постараемся понять, какие связанные с чертежом задачи мы умеем решать.

Рис. 14

И такие задачи находятся. Например, если знать площадь треугольника ABC , то мы можем сначала найти площадь треугольника BMC , а затем и площадь треугольника BMN . Когда это удалось отыскать, то дальнейшее уже не так сложно и приводит к следующему решению. , аналогично ,, , откуда .

Скачать архив с текстом документа