Расчет индексов цены и стоимости. Размер показателя реализованной продукции
СОДЕРЖАНИЕ: Определение размера планового задания по росту объема реализованной продукции. Расчет показателя динамики реализованной продукции. Изучение структуры жилищного фонда по формам собственности. Определение индивидуальных и общих индексов цены и стоимости.Задание № 1
Задача 1.
По представленным в таблице 2 данным по предприятиям фирмы определить в целом по фирме:
1) размер планового задания по росту объема реализованной продукции в 2005 г.;
2) процент выполнения плана пo объему реализованной продукции в 2005 г.;
3) показатель динамики реализованной продукции.
Таблица 1
| № варианта | № предприятия, входящего в фирму | Фактический объем реализованной продукции в 2004 г., млн.руб. | Плановое задание по росту реализованной продукции на 2004г., % | Фактический объем реализованной продукции в 2005 г., млн. руб. |
1 |
1 2 3 |
30,0 48,5 60,0 |
104,0 106,0 102,5 |
32,6 52,7 63,0 |
Решение:
1) ![]() 105,2%
105,2%
2) ![]() 103,2%
103,2%
3) ![]() 108,7%
108,7%
Задача 2.
Общая площадь жилищного фонда (тыс. кв. м.) по формам собственности в г.Санкт-Петербурге за период 1990-2002 гг. (на конец года) представлена в Таблице 2.
Определить:
1) структуру жилищного фонда по формам собственности;
2) динамику жилищного фонда по формам собственности и в целом по городу;
3) охарактеризовать изменения в соотношениях государственного (муниципального) и частного жилищного фонда с помощью относительного показателя координации.
Таблица 2
| № варианта | Показатель | Предыдущий период | Текущий период |
1 |
Жилищный фонд В том числе: Частный Государственный и муниципальный Общественных организаций Организаций прочих форм собственности |
88342 13621 74594 127 – |
89443 32691 56751 1 – |
Решение:
1) Структура жилищного фонда по формам собственности
| показатель | всего, тыс. кв. м. | удельный вес, % | ||
| предыдущий период | текущий период | предыдущий период | текущий период | |
| жилищный фонд | 88342 | 89443 | 100,00 | 100,00 |
| в том числе: | ||||
| частный | 13621 | 32691 | 15,42 | 36,55 |
| государственный и муниципальный | 74594 | 56751 | 84,44 | 63,45 |
| общественных организаций | 127 | 1 | 0,14 | 0,00 |
| организаций прочих форм собственности | - | - | - | |
2) Динамика жилищного фонда по формам собственности
| показатель | всего, тыс. кв. м. | в процентах к предыдущему году | |
| предыдущий период | текущий период | ||
| жилищный фонд | 88342 | 89443 | 101,25 |
| в том числе: | |||
| частный | 13621 | 32691 | 240,00 |
| государственный и муниципальный | 74594 | 56751 | 76,08 |
| общественных организаций | 127 | 1 | 0,79 |
| организаций прочих форм собственности | - | - | - |
3) относительный показатель координации
| показатель | всего, тыс. кв. м. | относительный показатель координации, % | ||
| предыдущий период | текущий период | предыдущий период | текущий период | |
| жилищный фонд | 88342 | 89443 | - | - |
| в том числе: | ||||
| частный | 13621 | 32691 | 100,0 | 100,0 |
| государственный и муниципальный | 74594 | 56751 | 547,6 | 173,6 |
| общественных организаций | 127 | 1 | 0,9 | 0,0 |
| организаций прочих форм собственности | - | - | - | |
Задача 3.
По представленным в Таблице 2 данным о затратах на производство продукции по двум предприятиям фирмы определить изменение (в %) доли затрат на оплату труда в общих затратах на производство в целом по фирме в отчетном году по сравнению с прошлым годом.
Таблица 3
| № варианта | № предприятия, входящего в фирму | Прошлый год | Отчетный год | ||
| Доля затрат на оплату труда в общих затратах на производство, % | Общие затраты на производство млн. руб. |
Затраты на оплату труда, млн. руб. | Доля затрат на оплату труда в общих затратах на производство, % | ||
| 1 | 1 2 |
18,0 19,5 |
200 180 |
40,7 38,0 |
18,5 20,2 |
Решение:
Прошлый год:
Средняя гармоническая взвешенная
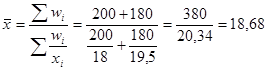 %
%
Отчетный год:
Средняя арифметическая взвешенная
 %
%
19,32:18,68*100%=103,426%
Доля затрат на оплату труда в отчетном по сравнению с базисным увеличилась на 3,43%.
Задание № 2
На основе данных, приведенных в Таблице 4 (Приложение 1) и соответствующих Вашему варианту, выполнить:
1. На основе структурной группировки построить вариационный частотный и кумулятивный ряды распределения, используя равные закрытые интервалы, приняв число групп равным 6. Результаты представить в виде таблицы и изобразить графически.
2. Проанализировать вариационный ряд распределения, вычислив:
- среднее арифметическое значение признака;
- моду, медиану, 1-ый квартиль, 1-ый и 9-тый дециль;
- среднее квадратичное отклонение;
- коэффициент вариации.
3. Сделать выводы.
Решение:
1. Используем данные о курсовой цене акций предприятия, руб. Количество групп – 6. Тогда величина интервала:
![]()
Для большей наглядности ряда распределения возьмем величину интервала равной 25.
Структурная группировка.
| курсовая цена акций предприятия, руб. | число предприятий | удельный вес, % |
| 30-55 | 17 | 34 |
| 55-80 | 14 | 28 |
| 80-105 | 11 | 22 |
| 105-130 | 3 | 6 |
| 130-155 | 1 | 2 |
| 155-185 | 4 | 8 |
| итого | 50 | 100 |

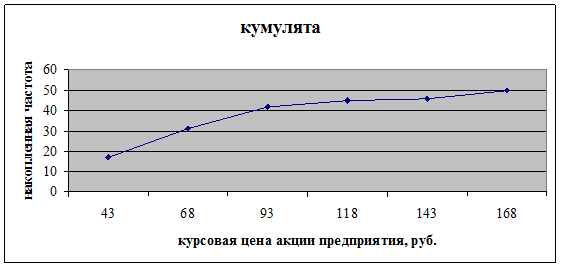
Кумулятивный ряд распределения
| курсовая цена акций предприятия, руб. | число предприятий | середина интервала | накопленная частота |
| 30-55 | 17 | 43 | 17 |
| 55-80 | 14 | 68 | 31 |
| 80-105 | 11 | 93 | 42 |
| 105-130 | 3 | 118 | 45 |
| 130-155 | 1 | 143 | 46 |
| 155-185 | 4 | 168 | 50 |
| итого | 50 | - | - |
2-3. Расчетная таблица
курсовая цена акций предприятия, руб. |
fi | xi | si | xi*fi | (xi-x ср )2*fi |
| 30-55 | 17 | 43 | 17 | 731 | 20234,25 |
| 55-80 | 14 | 68 | 31 | 952 | 1263,5 |
| 80-105 | 11 | 93 | 42 | 1023 | 2642,75 |
| 105-130 | 3 | 118 | 45 | 354 | 4920,75 |
| 130-155 | 1 | 143 | 46 | 143 | 4290,25 |
| 155-185 | 4 | 168 | 50 | 672 | 32761 |
| итого | 50 | - | - | 3875 | 66112,5 |
Среднее арифметическое значение признака
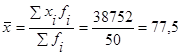 руб.
руб.
Средний размер курсовой цены акции по всем предприятиям составляет 77,5 руб.
Мода
![]() руб.
руб.
Наиболее часто в данной совокупности предприятий встречается цена – 51,25 руб.
Медиана
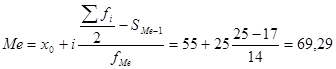 руб.
руб.
Половина предприятий имеет цену ниже 60,29 рублей, а половина – выше.
1-ый квартиль
 руб.
руб.
25% предприятий имеют курсовую цену акций меньше 48,38 руб.
1-ый дециль
 руб.
руб.
105% предприятий имеют курсовую цену акций меньше 37,35 руб.
9-ый дециль
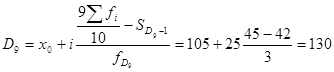 руб.
руб.
10% предприятий имеют курсовую цену акций выше 130 руб.
Среднее квадратическое отклонение
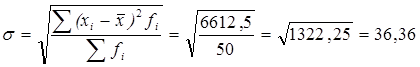 руб.
руб.
Значения курсовых цен акций предприятий отклоняются от средней цены (77,5) в среднем на 36,36 руб.
Коэффициент вариации
![]()
Совокупность предприятий по курсовой цене акция не однородна, т.к. коэффициент вариации выше 33%
Задание № 3
1. Используя результаты расчетов, выполненных в задании № 2 и полагая, что эти данные получены при помощи собственно-случайного 10-ти процентного бесповторного отбора, определить:
а) пределы, за которые с доверительной вероятностью 0,954 не выйдет среднее значение признака, рассчитанное по генеральной совокупности;
б) как нужно изменить объем выборки, чтобы снизить предельную ошибку средней величины на 50%.
2. Используя результаты расчетов, выполненных в задании № 2 и полагая, что эти данные получены при помощи повторного отбора, определить:
а) пределы, за которые в генеральной совокупности не выйдет значение доли предприятий, у которых индивидуальные значения признака превышают моду с доверительной вероятностью 0,954;
б) как изменить объем выборки, чтобы снизить предельную ошибку доли на 20 %.
Решение:
1. а) средняя по выборке ![]() ; N=500; t=2, т.к Р=0,954 (по таблице)
; N=500; t=2, т.к Р=0,954 (по таблице)
Предельная ошибка выборки:
![]()
Доверительный интервал для средней:
![]() ;
; ![]()
По полученным результатам можно сказать, что средний размер курсовой цены акции в генеральной совокупности с вероятностью 0,954 находится в пределах от 67,7 до 87,3 руб.
б) уменьшить предельную ошибку на 50%
![]()
![]() предприятия
предприятия
При снижении предельной ошибки на 50% необходимо увеличить выборку до 153 предприятий.
2. а) ![]()
![]()
Доверительный интервал для доли
![]() ;
; ![]()
![]()
По полученным результатам можно сказать, что доля предприятий, имеющих средний размер курсовой цены акции меньше моды, в генеральной совокупности с вероятностью 0,954 находится в пределах от 21 до 47%.
б) снизить предельную ошибку доли на 20%
![]()
![]() предприятия
предприятия
При снижении предельной ошибки на 20% необходимо увеличить выборку до 83 предприятий.
Задание № 4
I. Используя данные Таблицы 5 :
1). Определить индивидуальные индексы:
* физического объема,
* цены;
* стоимости.
2). Определить общие индексы:
* физического объема,
* цены;
* стоимости.
Объяснить экономический смысл каждого из индексов, показать взаимосвязь между ними.
3). Определить абсолютное изменение стоимости произведенной продукции в текущем периоде по сравнению с базисным, в том числе, за счет изменения цен и за счет изменения выпуска продукции.
4). Считая продукцию однородной, определить как изменилась средняя цена единицы продукции и как при этом повлияло изменение цен и изменение структуры выпускаемой продукции. Объяснить полученные результаты.
Таблица 5
№ варианта |
Вид продукции |
Базисный период | Текущий период | ||
| Выпуск продукции, тыс.шт. | Цена за единицу, тыс. руб./шт. | Выпуск продукции, тыс.шт. |
Цена за единицу, тыс. руб./шт. | ||
1 |
I II III |
66 46 58 |
120 140 100 |
72 80 48 |
150 160 110 |
Решение:
1). Определить индивидуальные индексы:
* физического объема,
* цены;
* стоимости
Результаты представим в таблице:
вид продукции |
стоимость, руб. | индивидуальные индексы, % | ||||
| баз. | отчет. | усл. | физ.объема | цен | ст-ти | |
| 1 | 7920 | 10800 | 8640 | 109,09 | 125,00 | 136,36 |
| 2 | 6440 | 12800 | 11200 | 173,91 | 114,29 | 198,76 |
| 3 | 5800 | 5280 | 4800 | 82,76 | 110,00 | 91,03 |
| итого | 20160 | 28880 | 24640 | |||
2). Определить общие индексы:
Физического объема
![]()
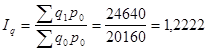
Цены
![]()
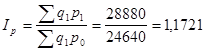
Стоимости
![]()
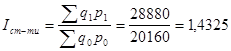
Взаимосвязь индексов
![]()
По каждому из видов продукции цены увеличились, а количество по первым двум видам увеличилось, а по третьему уменьшилось. Стоимость изменилась аналогично количеству по отдельным видам продукции.
В целом по трем товарам цены увеличились на 17,21%, количество увеличилось на 22,22%, стоимость увеличилась также на 43,25%.
3) Абсолютные изменения
Стоимости
![]() руб.
руб.
За счет изменения цен
![]() руб.
руб.
За счет изменения количества
![]() руб.
руб.
4) Индекс переменного состава
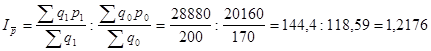
Индекс постоянного состава

Индекс структурных сдвигов
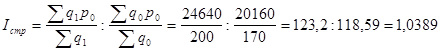
Средняя цена по совокупности увеличилась в отчетном периоде по сравнению с базисным на 21,76%, за счет цен по отдельным товарам увеличилась на 17,21%, а за счет структурных изменений на 3,89%.
II. Используя данные Таблицы 6 рассчитать, как в среднем изменилась себестоимость единицы и выпуск продукции
Таблица 6
№ варианта |
Вид продукции |
Изменение себестоимости единицы продукции в текущем периоде по сравнению с базисным, % | Изменение физического объема продукции в текущем периоде по сравнению с базисным, % | Затраты на производство продукции, (млн. руб.) | |
| Базисный период | Текущий период | ||||
1 |
А В С |
93 102 96 |
120 112 113 |
25 14 48 |
28 16 52 |
Решение:
Индекс себестоимости
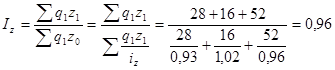
В среднем себестоимость уменьшилась на 4%.
Индекс физического объема
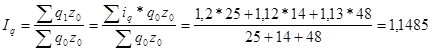
В среднем выпуск продукции увеличился на 14,85%.
Задание № 6
По данным Таблицы 7 (Приложение 2) выбрать динамический ряд, соответствующий Вашему варианту, для которого:
1. Рассчитать:
а) среднегодовой уровень ряда динамики;
б) цепные и базисные показатели динамики: абсолютный прирост, темп роста, темп прироста;
в) средний абсолютный прирост, средний темп роста, средний темп прироста.
2. Произвести сглаживание ряда динамики трехлетней скользящей средней.
3. Изобразить фактический и выровненный ряды графически.
4.Сделать выводы.
Решение:
Объем производства продукции, тыс. руб.
1. Расчетная таблица:
| годы | объем, тыс. руб. |
абсолютный прирост, тыс.т. | темп роста, % | темп прироста, % | |||
| цепной | базисный | цепной | базисный | цепной | базисный | ||
| 1994 | 800 | - | - | - | - | - | - |
| 1995 | 864 | 64 | 64 | 108,00 | 108,00 | 8,00 | 8,00 |
| 1996 | 970 | 106 | 170 | 112,27 | 121,25 | 12,27 | 21,25 |
| 1997 | 1006 | 36 | 206 | 103,71 | 125,75 | 3,71 | 25,75 |
| 1998 | 1035 | 29 | 235 | 102,88 | 129,38 | 2,88 | 29,38 |
| 1999 | 1174 | 139 | 374 | 113,43 | 146,75 | 13,43 | 46,75 |
| 2000 | 1287 | 113 | 487 | 109,63 | 160,88 | 9,63 | 60,88 |
| 2001 | 1341 | 54 | 541 | 104,20 | 167,63 | 4,20 | 67,63 |
| 2002 | 1475 | 134 | 675 | 109,99 | 184,38 | 9,99 | 84,38 |
| 2003 | 1539 | 64 | 739 | 104,34 | 192,38 | 4,34 | 92,38 |
| 2004 | 1712 | 173 | 912 | 111,24 | 214,00 | 11,24 | 114,00 |
Среднегодовой уровень:
![]() тыс. руб.
тыс. руб.
Средний абсолютный прирост
![]() тыс.руб.
тыс.руб.
Средний темп роста
![]()
Средний темп прироста
![]() +8%
+8%
2. Сглаживание по трехлетней средней представлено в таблице:
| годы | тыс. руб. | трехлетняя средняя |
| 1994 | 800 | - |
| 1995 | 864 | 878 |
| 1996 | 970 | 947 |
| 1997 | 1006 | 1004 |
| 1998 | 1035 | 1072 |
| 1999 | 1174 | 1165 |
| 2000 | 1287 | 1267 |
| 2001 | 1341 | 1368 |
| 2002 | 1475 | 1452 |
| 2003 | 1539 | 1575 |
| 2004 | 1712 | - |
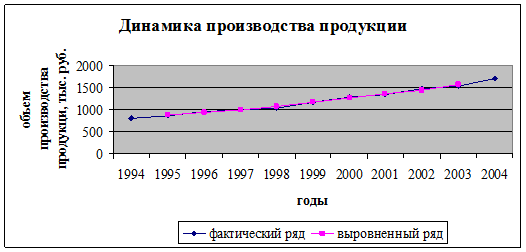
Объем производства повышался в течение всего анализируемого периода.