Расчет каналов

СОДЕРЖАНИЕ: Санкт-Петербургский Государственный политехнический университет Кафедра Гидравлики Задание № 4 по курсу Механика жидкости и газа (гидравлика) «РАСЧЕТ КАНАЛОВ»

Санкт-Петербургский Государственный политехнический университет

Кафедра Гидравлики

Задание № 4

по курсу Механика жидкости и газа (гидравлика)

«РАСЧЕТ КАНАЛОВ»

Выполнил: студент

группы 3013/2

Мозалевский А.А.

Приняла:

Локтионова Е.А.

Санкт-Петербург

2010


Оглавление

1. Расчёт каналов на равномерное движение

1.1 Определение глубины равномерного движения и ширины канала по дну на подводящем участке канала

1.2 Определение глубины равномерного движения на отводящем участке канала

1.3 Определение средней скорости движения воды в канале

1.4 Определение глубины наполнения и уклона дня канала

2. Расчёт каналов на неравномерное движение

2.1 Определение критической глубины и критического уклона

2.2 Построение графика удельной энергии сечения Э(h)

2.3 Построение кривой свободной поверхности на подводящем участке канала

2.4 Построение кривых свободной поверхности на отводящем участке канала

2.5 Построение кривой свободной поверхности в канале при открытом затворе

3 Расчёт отводящего участка канала при наличии гидравлического прыжка

3.1 Построение графика прыжковой функции

3.2 Определение местоположения гидравлического прыжка

3.3 Определение параметров гидравлического прыжка

Список использованной литературы


1. Расчёт каналов на равномерное движение

1.1 Определение глубины равномерного движения и ширины канала по дну на подводящем участке канала

Дано:

1) расход воды в канале м3/с;

2) коэффициент откоса канала;

3) уклон дна подводящего участка канала;

4) коэффициент шероховатости;

5) относительная ширина

Найти: - глубину равномерного движения,

– ширина канала по дну.

Подсчитаем необходимый модуль расхода при заданном расходе воды в канале и уклоне дна подводящего участка канала:

.

,

где - геометрически наивыгоднейшее сечение;

;

.

Решение произведём методом подбора. Для этого зададимся нормальной глубиной и найдём значения , где

- площадь живого сечения,

- смоченный периметр,

- гидравлический радиус,

- коэффициент Шези,

– модуль расхода.

м 1,5 1,75 2 2,5 3
м 5,4 6,3 7,2 9 10,8
м2 13,05 17,76 23,2 36,25 52,2
м 12,65 14,76 16,86 21,1 25,23
м 1,03 1,21 1,37 1,72 2,06
47,86 49,1 50,2 52,12 53,73
634,46 957,05 1366,4 2477,45 4028,6

Пример расчёта таблицы для м:

1) Используя заданную глубину, найдём значение ширины канала по дну:

м;

2) Определим площадь живого сечения:

м2 ;

3) Найдём значение смоченного периметра:

;

4) Определим гидравлический радиус:

;

5) Найдём значение коэффициента Шези:

;

6) Определим модуль расхода:

;

Построим график зависимости hО от K и определим значение :

м, отсюда

м.

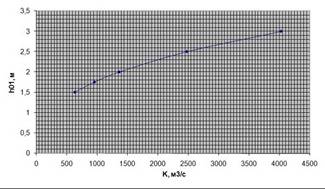
Рис. 1. График зависимости hО1 от K.

1.2 Определение глубины равномерного движения на отводящем участке канала

Дано:

1) расход воды в канале м3 /с;

2) коэффициент откоса канала ;

3) уклон дна отводящего участка канала ;

4) коэффициент шероховатости ;

5) ширина канала по дну м.

Найти: - глубину равномерного движения.

Решение произведём методом подбора. Для этого зададимся нормальной глубиной и , используя полученное в предыдущем пункте значение м, найдём значения .

м 1,5 2 2,5 3 3,25
м 8,28 8,28 8,26 8,28 8,28
м2 17,37 25,36 34,45 44,64 50,15
м 15,53 17,94 20,36 22,78 24
м 1,12 1,4 1,7 1,96 2,1
48,5 50,44 51,98 53,27 52,84
891,26 1520,7 2329,17 3328,8 3904,22

Пример расчёта таблицы для м:

1) Определим площадь живого сечения, используя заданную глубину и ширину канала по дну:

м2 ;

2) Найдём значение смоченного периметра:

;

3) Определим гидравлический радиус:

;

4) Найдём значение коэффициента Шези:

;

5) Определим модуль расхода:

;

6) Подсчитаем необходимый модуль расхода при заданном расходе воды в канале и уклоне дна отводящего участка канала:

.

Построим график зависимости hО от K и определим значение по значению (рис.2): м.


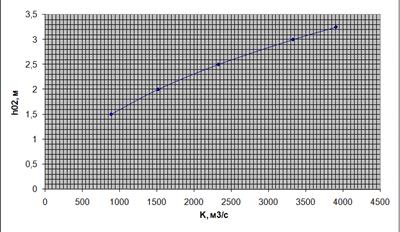
Рис. 2. График зависимости hО2 от K.

1.3Определение средней скорости движения воды в канале

;

; где

- значение средней скорости на подводящем участке канала,

- значение средней скорости на отводящем участке канала.

Определим площади живых сечений на подводящем и отводящем участках канала:

м2 ,

м2 ,

тогда скорости будут равны:

м/с,

м/с.

м/с, м/с при среднем размере частиц грунта мм ([1], т.7.1, с.72) и м, м.

,

1.4Определение глубины наполнения и уклона дня канала

Т.к. , положим, что , тогда:

м2 ,

,

приравняв правые части равенств, получим:

м, отсюда:

м,

м,

,

,

.

Поперечные сечения каналов представлены на рис.3.


2. Расчёт каналов на неравномерное движение

2.1Определение критической глубины и критического уклона

,

где - критическая ширина канала по верху,

м5 .

Решение произведём методом подбора. Для этого зададимся критической глубиной и найдём значения .

м м2 м м5
1,3 14 14,48 216,95
1,4 14,44 15,90 278,58
1,5 14,88 17,37 352,21
1,6 15,32 18,88 439,28
1,7 15,76 20,34 541,382

Пример расчёта таблицы для м:

1) Определим площадь живого сечения, используя заданную глубину и ширину канала по дну:

м2 ;

2) Найдём значение ширины канала по верху:

м;

3) Определим отношение :

м5 ;

Построим график зависимости от (рис.5). Используя подсчитанное значение , найдём: м,

где - критическая глубина.

Вычислим критический уклон дна по формуле:

,

где ,

,

.

1) Найдём критическое значение смоченного периметра:

м,

2) Вычислим критическое значение ширины канала по верху:

м,

3) Определим критическое значение гидравлического радиуса:

,

Где м2 , тогда

м,

4) Найдём критическое значение коэффициента Шези:

,

Следовательно, ;

,

.

2.2Построение графика удельной энергии сечения Э( h)

Для построения графика зададимся значениями глубины h и вычислим .

м м2 м/с м м
0,50 4,69 12,56 8,047 8,547
0,60 5,76 10,23 5,335 5,935
0,70 6,874 8,57 3,746 4,446
0,80 8,032 7,33 2,774 3,544
0,90 9,234 6,38 2,076 2,976
1,00 10,48 5,62 1,600 2,612
1,10 11,77 5,00 1,278 2,378
1,20 13,104 4,49 1,030 2,231
1,30 14,482 4,07 0,844 2,144
1,40 15,904 3,70 0,700 2,100
1,50 17,37 3,39 0,587 2,087
1,60 18,88 3,12 0,497 2,097
1,90 23,67 2,49 0,32 2,220
2,3 30,68 1,92 0,19 2,490
3,5 55,93 1,05 0,06 3,56

Пример расчёта таблицы для м:

1) Определим площадь живого сечения, используя заданную глубину и ширину канала по дну:

м2 ;

2) Найдём значение скорости:

м/с;

3) Вычислим значение скоростного напора:

м;

4) Определим значение удельной энергии сечения:

м.

График удельной энергии сечения Э(h) приведён на рис.6.

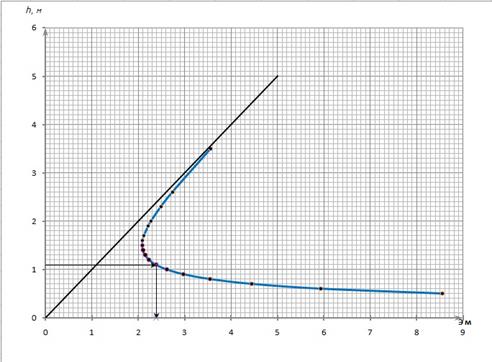
Рис. 6. График удельной энергии сечения Э (h).

2.3 Построение кривой свободной поверхности на подводящем участке канала

Для построения примем постоянный шаг по глубине:

м,

тем самым разобьём подводящий участок канала на 10 равных частей.

Так как и , то строим кривую типа (рис.7). Рассчитаем её длину по таблице:


м м2 м/с м м м м м2 м м м
1 9,12 258,50 0,228 0,0026 9,123 0,433 8,9035 248,120 51,313 4,835 61,923 0,0000030 0,0000660 6557,28
8,687 237,95 0,248 0,0031 8,690
2 8,687 237,95 0,248 0,0031 8,690 0,432 8,471 227,984 49,220 4,632 61,481 0,0000038 0,0000652 6633,29
8,254 218,23 0,270 0,0037 8,258
3 8,254 218,23 0,270 0,0037 8,258 0,432 8,038 208,674 47,127 4,428 61,021 0,0000048 0,0000642 6736,43
7,821 199,33 0,295 0,0045 7,825
4 7,821 199,33 0,295 0,0045 7,825 0,432 7,605 190,188 45,034 4,223 60,542 0,0000062 0,0000628 6879,64
7,388 181,25 0,325 0,0054 7,393
5 7,388 181,25 0,325 0,0054 7,393 0,432 7,172 172,527 42,941 4,018 60,040 0,0000080 0,0000610 7084,32
6,955 164,01 0,359 0,0066 6,962
6 6,955 164,01 0,359 0,0066 6,962 0,431 6,739 155,691 40,849 3,811 59,515 0,0000106 0,0000584 7388,11
6,522 147,58 0,399 0,0081 6,530
7 6,522 147,58 0,399 0,0081 6,530 0,431 6,306 139,680 38,756 3,604 58,963 0,0000142 0,0000548 7863,04
6,089 131,98 0,446 0,0102 6,099
8 6,089 131,98 0,446 0,0102 6,099 0,430 5,873 124,494 36,663 3,396 58,380 0,0000193 0,0000497 8664,69
5,656 117,21 0,503 0,0129 5,669
9 5,656 117,21 0,503 0,0129 5,669 0,429 5,440 110,133 34,570 3,186 57,763 0,0000269 0,0000421 10198,80
5,223 103,26 0,570 0,0166 5,240
10 5,223 103,26 0,570 0,0166 5,240 0,428 5,007 96,597 32,478 2,974 57,105 0,0000383 0,0000307 13950,33
4,79 90,14 0,653 0,0218 4,812
81955,93

Пример расчёта таблицы для м:

1) Определим площадь живого сечения, используя заданную глубину и ширину канала по дну:

м2 ;

2) Найдём значение скорости:

м/с;

3) Вычислим значение скоростного напора:

м;

4) Определим значение удельной энергии сечения:

м;

5) Найдём разницу удельной энергии сечения на соседних участках:

м;

6) Вычислим среднее значение глубины:

м;

7) Определим среднее значение площади живого сечения:

м;

8) Найдём среднее значение смоченного периметра:

м;

9) Вычислим среднее значение гидравлического радиуса:

м;

10) Определим среднее значение коэффициента Шези:

;

11) Найдём значение среднего уклона трения:

;

12) Вычислим разницу между уклоном дна подводящего участка, пересчитанным в соответствии со значением максимальной неразмывающей скорости, и средним уклоном трения:

;

13) Определим длину участка с помощью уравнения Чарномского:


м.

Находим длину кривой свободной поверхности:

м.

2.4 Построение кривых свободной поверхности на отводящем участке канала

1. Для построения примем постоянный шаг по глубине:

м, тем самым разобьём отводящий участок канала на 5 равных частей.

Так как и , то строим кривую типа (рис.8). Рассчитаем её длину по таблице:


Nуч h V Э Эm+1 -Эm h R C if i2-if l
м м2 м/с м м м м м2 м м м
1 0,44 4,07 14,475 10,679 11,119 -4,129 0,496 4,648 10,677 0,435 41,456 0,2146 -0,2101 19,65
0,552 5,24 11,239 6,438 6,990
2 0,552 5,24 11,239 6,438 6,990 -2,099 0,608 5,848 11,219 0,521 42,719 0,1067 -0,1022 20,54
0,664 6,47 9,107 4,227 4,891
3 0,664 6,47 9,107 4,227 4,891 -1,171 0,720 7,102 11,760 0,604 43,780 0,0594 -0,0549 21,32
0,776 7,75 7,600 2,944 3,720
4 0,776 7,75 7,600 2,944 3,720 -0,691 0,832 8,412 12,301 0,684 44,696 0,0359 -0,0314 22,01
0,888 9,09 6,481 2,141 3,029
5 0,888 9,09 6,481 2,141 3,029 -0,419 0,944 9,777 12,843 0,761 45,503 0,0230 -0,0185 22,63
1 10,48 5,620 1,610 2,610
106,15

Пример расчёта таблицы для м:

1) Определим площадь живого сечения, используя заданную глубину и ширину канала по дну:

м2 ;

2) Найдём значение скорости:

м/с;

3) Вычислим значение скоростного напора:

м;

4) Определим значение удельной энергии сечения:

м;

5) Найдём разницу удельной энергии сечения на соседних участках:

м;

6) Вычислим среднее значение глубины:

м;

7) Определим среднее значение площади живого сечения:

м;

8) Найдём среднее значение смоченного периметра:

м;

9) Вычислим среднее значение гидравлического радиуса:

м;

10) Определим среднее значение коэффициента Шези:

;

11) Найдём значение среднего уклона трения:

;

12) Вычислим разницу между уклоном дна отводящего участка и средним уклоном трения:

;

13) Определим длину участка с помощью уравнения Чарномского:

м.

Находим длину кривой свободной поверхности:

м.

2. Для построения кривой типа (рис.9) составим таблицу, назначив шаг по глубине так, чтобы и разбив отводящий участок канала на 5 частей.

Пример расчёта таблицы для м:

1) Определим площадь живого сечения, используя заданную глубину и ширину канала по дну:

м2 ;

2) Найдём значение скорости:

м/с;

3) Вычислим значение скоростного напора:

м;

4) Определим значение удельной энергии сечения:

м;

5) Найдём разницу удельной энергии сечения на соседних участках:


м;

6) Вычислим среднее значение глубины:

м;

7) Определим среднее значение площади живого сечения:

м;

8) Найдём среднее значение смоченного периметра:

м;

9) Вычислим среднее значение гидравлического радиуса:

м;

10) Определим среднее значение коэффициента Шези:

;

11) Найдём значение среднего уклона трения:

;

12) Вычислим разницу между уклоном дна отводящего участка и средним уклоном трения:

;

13) Определим длину участка с помощью уравнения Чарномского:

м.


№ уч-ка h, м , м2 , м/с , м Э, м Эm +1 -Эm , м , м , м2 , м , м ,
, м
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
I 1,105 14,178 3,01 0,46 1,565 -0,040 1,195 15,587 16,176 0,963 70,981 15,47 -14,99 26,68
1,285 16,997 2,51 0,32 1,605
II 1,285 16,997 2,51 0,32 1,605 -0,070 1,360 18,225 16,973 1,074 72,283 9,78 -9,30 75,27
1,435 19,454 2,19 0,24 1,675
III 1,435 19,454 2,19 0,24 1,675 -0,070 1,485 20,301 17,577 1,155 73,165 7,15 -6,67 104,95
1,535 21,148 2,02 0,21 1,745
IV 1,535 21,148 2,02 0,21 1,745 -0,070 1,585 22,016 18,061 1,219 73,825 5,66 -5,18 135,13
1,635 22,885 1,86 0,18 1,815
V 1,635 22,885 1,86 0,18 1,815 -0,076 1,688 23,830 18,558 1,284 74,467 4,51 -4,03 188,59
1,741 24,775 1,72 0,15 1,891

Находим длину кривой свободной поверхности типа на отводящем участке канала:


2.5 Построение кривой свободной поверхности в канале при открытом затворе

Для построения кривой типа на подводящем участке канала (рис.9) составим таблицу, разбив его на две части и назначив шаг по глубине так, чтобы .

Пример расчёта таблицы для м:

1) Определим площадь живого сечения, используя заданную глубину и ширину канала по дну:

м2 ;

2) Найдём значение скорости:

м/с;

3) Вычислим значение скоростного напора:

м;

4) Определим значение удельной энергии сечения:

м;

5) Найдём разницу удельной энергии сечения на соседних участках:

м;

6) Вычислим среднее значение глубины:

м;

7) Определим среднее значение площади живого сечения:

м;

8) Найдём среднее значение смоченного периметра:

м;

9) Вычислим среднее значение гидравлического радиуса:

м;

10) Определим среднее значение коэффициента Шези:

;

11) Найдём значение среднего уклона трения:

;

12) Вычислим разницу между уклоном дна подводящего участка и средним уклоном трения:

;

13) Определим длину участка с помощью уравнения Чарномского:

м.


№ уч-ка h, м , м2 , м/с , м Э, м Эm +1 -Эm , м , м , м2 , м , м ,
, м
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
I 1,741 24,775 1,72 0,15 1,891 -0,060 1,781 25,504 19,008 1,342 75,018 3,71 -3,51 170,94
1,821 26,234 1,63 0,13 1,951
II 1,821 26,234 1,63 0,13 1,951 -0,103 1,877 27,288 19,472 1,401 75,558 3,06 -2,86 360,14
1,934 28,342 1,51 0,12 2,054

Находим длину кривой свободной поверхности типа на подводящем участке канала:


3. Расчёт отводящего участка канала при наличии гидравлического прыжка

3.1 Построение графика прыжковой функции

Найдем значения прыжковой функции для различных значений глубины наполнения канала. Вычисления сведём в таблицу, по результатам которой построим график зависимости прыжковой функции от глубины наполнения (рис. 6).

№, п/п
м м м м2 м3 м3 м3
1 0,40 12,16 0,195 4,51 41,25 0,88 42,13
2 0,60 13,04 0,289 7,03 26,46 2,03 28,49
3 0,80 13,92 0,381 9,73 19,12 3,71 22,83
4 0,90 14,36 0,426 11,14 16,70 4,75 21,45
5 1,105 15,26 0,518 14,18 13,12 7,34 20,46
6 1,25 15,90 0,581 16,44 11,32 9,55 20,87
7 1,30 16,12 0,603 17,24 10,79 10,39 21,18
8 1,32 16,21 0,612 17,56 10,59 10,75 21,34
9 1,35 16,34 0,625 18,05 10,31 11,28 21,59
10 1,50 17,00 0,690 20,55 9,05 14,18 23,23
11 1,70 17,88 0,775 24,04 7,74 18,63 26,37
12 1,90 18,76 0,859 27,70 6,72 23,79 30,51
13 2,00 19,20 0,901 29,60 6,28 26,67 32,95
14 2,50 21,40 1,106 39,75 4,68 43,96 48,64
15 3,00 23,60 1,306 51,00 3,65 66,61 70,26

Пример расчёта таблицы для м:

1) Найдём значение ширины канала по верху:

м;

2) Вычислим значение заглубления центра тяжести сечения под свободной поверхностью:

м;

3) Определим площадь живого сечения, используя заданную глубину и ширину канала по дну:

м2 ;

4) Вычислим значение произведения :

м3 ;

5) Найдём значение произведения :

= 0,1954,51 = 0,879 м3 ;

6) Определим величину прыжковой функции :

41,25 + 0,879 = 42,13 м3 .

3.2Определение местоположения гидравлического прыжка

Полагая, что все точки на кривой типа равновероятны для начала прыжка, составим таблицу:

м 0,592 0,720 0,848 0,976
м 1,840 1,610 1,398 1,180

Пользуясь свойством прыжковой функции , определим про графику соответствующие вторые сопряжённые глубины.

По данным таблицы на рисунке 8 наносим линию вторых сопряжённых глубин.

Точка пересечения линии с кривой типа соответствует действительной второй сопряжённой глубине.

Обратным ходом по графику по =1,67 м, находим м.

3.3 Определение параметров гидравлического прыжка

Высота прыжка м.

Длина прыжка равна м.

Потеря энергии в прыжке

;

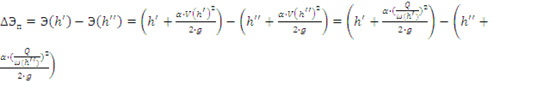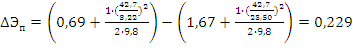м.

Наносим полученные значения на график (рис.6).

Схема гидравлического прыжка представлена на рис. 10.


Список использованной литературы

1. Механика жидкости и газа (гидравлика). Справочник: Учеб. пособие / Е.Н. Кожевникова, А.И. Лаксберг, Е.А. Локтионова, М.Р. Петриченко. СПб.: Изд-во Политехн. Ун-та, 2007. 90 с.

Скачать архив с текстом документа