Задачи по курсу общей физики для студентов астрономического отделения. (1)

СОДЕРЖАНИЕ: В основе предлагаемой работы лежит опыт семинарских занятий по курсам общей физики и астрономии для студентов астрономического отделения физического факуль­тета мгу

Бычков К.В.⁽¹⁾ , Сараева И.М.⁽²⁾

Кинематика материальной точки.

Задачи по курсу общей физики

для студентов астрономического отделения.

⁽¹⁾ Государственный астрономический институт им. П.К. Штернберга

⁽²⁾ Физический факультет МГУ, кафедра общей физики

Введение

В основе предлагаемой работы лежит опыт семинарских занятий по курсам общей физики и астрономии для студентов астрономического отделения физического факуль­тета МГУ.

При изучении механики материальной точки, в особенности её разделов, связанных с движением по криволинейной траектории, часто оказываются полезными астрономиче­ские приложения. В условиях поверхности Земли набор естественных траекторий прак­тически сводится к параболе. В космосе, наоборот, представлены многие типы криволи­нейного движения: вращение по окружности, а также эллиптические, параболические и гиперболические траектории разной степени вытянутости. К тому же формы орбит кос­мических объектов не ограничиваются одними коническими сечениями. Например, об­ращение звёзд вокруг центра галактики во многих случаях не описываются законами Кеплера, а в процессе сжатия вращающихся газовых туманностей имеет место посте­пенное приближение к центру по спирали. Параллельно с физическим содержанием за­дачи уместно привести и первые сведения о математическом аппарате плоских кривых линий.

Другим аспектом является соотношение между прямыми и обратными задачами. Для лабораторных условий типична прямая постановка: требуется вычислить параметры траектории тела, зная действующие на него силы. В астрономии как наблюдательной науке важен и обратный подход, когда по известному движению выясняют характер взаимодействия. Часть предлагаемого материала даёт студентам первое представление об обратных задачах. С методической точки зрения решение обратной задачи, как правило, проще и нагляднее. Поэтому имеет смысл показать одну и ту же задачу дважды: сначала в разделе «кинематика» как обратную, и затем, после приобретения студентами опыта, в разделе «динамика» выполнить решение более сложной прямой задачи. Перейдём к изложению материала, предварительно договорившись о некоторых обозначениях. Координаты точки, движущейся в плоскости, как обычно, равны x и y, время - t, а для параметров движения оставляем буквы a, b, k, w, j. Векторы представляем прямыми жирными символами: r – радиус вектор частицы, v – её скорость, w – ускорение. Точка над символом описывает дифференцирование по времени.

I Определение траектории, скорости и ускорения точки из закона движения в декартовых координатах.

Во всех задачах этого раздела требуется определить форму траектории, найти векторы скорости и ускорения, а также восстановить динамический закон движения.

Задача 1. Точка движется в плоскости. Её координаты x и y зависят от времени t как

( 1)

( 2)

где a, b, и - параметры.

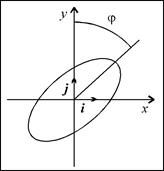
Если a либо b равны нулю, то имеет место прямолинейное движение вдоль той или иной координатной оси. Оно происходит внутри отрезка длиной 2a , либо 2b, центр которого расположен в начале координат. Предположим, что оба этих параметра отличны от нуля. Разделим первое уравнение на a, второе - на b и раскроем косинус суммы:

, ( 3 )

. ( 4 )

Исключим время t из уравнений движения. Сначала рассмотрим два особых случая. При получается эллипса, ориентированный параллельно осям:

,

а значению соответствует уравнение отрезка прямой .

В случае, когда оба этих параметра отличны от нуля, с помощью ( 3 ) выразим и через x/a и подставим результат в ( 4 ). После несложных преобразований получим уравнение эллипса, ориентация которого определяется величиной :

Рис. 1. Наклонный эллипс.

.

Роль параметра ясна из Рис. 1. Теперь определим кинематические характеристики траектории и попытаемся выяснить направление действующей силы. На Рис. 1 единичные векторы i и j , направлены вдоль координатных осей. Напишем выражение для радиус-вектора точки, с координатами ( 1 ) и ( 2 ):

.

Векторы скорости и ускорения получаются последовательным дифференцированием r:

,

.

Из последних двух формул вытекает связь между ускорением и радиус-вектором:

. ( 5 )

Мы получили хорошо известное уравнение пространственного осциллятора. Частица массы m движется под действием центральной притягивающей силы, по абсолютной величине равной m² r .

Пространственный осциллятор является важным методическим инструментом в атомной физике и оптике — двух активно используемых в астрофизике разделах общей физики. Знакомство с ним на семинарах по механике облегчает в дальнейшем освоение темы поляризованного излучения, а также анализ эффектов Зеемана и Штарка.

Задача 2 Точка движется по закону

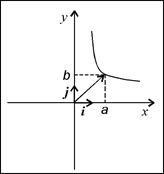
с параметрами a , b и k . Случай k= 0 здесь не представляет интереса. Равенство нулю a или b означает прямолинейное перемещение вдоль одной из координатных осей. Если они оба отличны от нуля, то траектория является отрезком гиперболы y=ab/x .

Рис. 2. Гипербола y=ab/x .

Не теряя общности, мы можем считать a и b положительными[1] . Они равны координатам точки в начальный момент времени:

,

которая в дальнейшем будет двигаться вправо. Вычислим вектор скорости

,

его абсолютную величину

и вектор ускорения

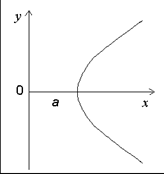
Рис. 3.Повёрнутая гипербола

.

Тело отталкивает центральная сила mk ² r.

Задача 3. Точка движется в плоскости :

, ( 6)

. ( 7 )

Вычтем квадраты уравнений, делённых на a и b соответственно:

.

Получилась гипербола, как и на Рис. 2, но оси координат повёрнуты на 45°. Её график приведён на Рис. 3. Дифференцируя (6) и (7) по времени, получим вектор скорости

и ускорения

.

Легко убедиться, что и здесь на тело действует отталкивающая сила F= mk² r . Итак, одна и та же сила может обуславливать внешне различающиеся типы движения. На частном примере мы увидели проявление важного принципа: динамический закон является более общей характеристикой движения, чем кинематические параметры.

Рис. 4. Винтовая линия

Задача 4. Заряженная частица совершает пространственное движение в однородном и постоянном магнитном поле:

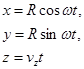
с постоянными параметрами R, v_z, w . Складывая квадраты первых двух уравнений, получаем винтовую линию

с шагом. Винтовая линия изображена на Рис. 4. Из закона движения вытекают следующие выражения для вектора скорости

и квадрата его модуля [1] Знаки a и b определяют квадрант, в котором находится гипербола.

Скачать архив с текстом документа