Расчет коэффициента эластичности и показателей корреляции и детерминации
СОДЕРЖАНИЕ: Построение поля корреляции, расчет уравнений линейной парной регрессии, на основе данных о заработной плате и потребительских расходах в расчете на душу населения. Анализ коэффициента эластичности, имея уравнение регрессии себестоимости единицы продукции.МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
Ульяновская государственная сельскохозяйственная академия
Кафедра «Статистика и анализ хозяйственной деятельности»
Контрольная работа
по Эконометрики
Выполнил: студент 2 курса
заочного отделения «Экономического факультета»
по специальности «Финансы и кредит»
с сокращенным сроком обучения
Антонов Леонид Владимирович
Ульяновск, 2009
Задача 1
По территориям Волго-Вятского, Центрально–Черноземного и Поволжского районов известны данные о потребительских расходах в расчете на душу населения, о средней заработной плате и выплатах социального характера (табл. 1).
Таблица 1
| Район | Потребительские расходы в расчете на душу населения, руб., y | Средняя заработная плата и выплаты социального характера, руб., x |
| 1 | 408 | 524 |
| 2 | 249 | 371 |
| 3 | 253 | 453 |
| 4 | 580 | 1006 |
| 5 | 651 | 997 |
| 6 | 322 | 486 |
| 7 | 899 | 1989 |
| 8 | 330 | 595 |
| 9 | 446 | 1550 |
| 10 | 642 | 937 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнений линейной парной регрессии.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи факторов с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F- критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп.4,5 и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 7 % от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости, а = 0,05.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнений линейной парной регрессии.
| y | x | yx | x2 | y2 | x | y-x | Ai | |
| 1 | 408 | 524 | 213792 | 274576 | 166464 | 356,96 | 51,04 | 12,5 |
| 2 | 249 | 371 | 92379 | 137641 | 62001 | 306,47 | -57,47 | 23,1 |
| 3 | 253 | 453 | 114609 | 205209 | 64009 | 333,53 | -80,53 | 31,8 |
| 4 | 580 | 1006 | 583480 | 1012036 | 336400 | 516,02 | 63,98 | 11,0 |
| 5 | 651 | 997 | 649047 | 994009 | 423801 | 513,05 | 137,95 | 21,2 |
| 6 | 322 | 486 | 156492 | 236196 | 103684 | 344,42 | -22,42 | 7,0 |
| 7 | 899 | 1989 | 1788111 | 3956121 | 808201 | 840,41 | 58,59 | 6,5 |
| 8 | 330 | 595 | 196350 | 354025 | 108900 | 380,39 | -50,39 | 15,3 |
| 9 | 446 | 1550 | 691300 | 2402500 | 198916 | 695,54 | -249,54 | 56,0 |
| 10 | 642 | 937 | 601554 | 877969 | 412164 | 493,25 | 148,75 | 23,2 |
| итого | 4780 | 8908 | 5087114 | 10450282 | 2684540 | 4780,04 | -0,04 | 207,5 |
| среднее значение | 478 | 890,8 | 508711,4 | 1045028,20 | 268454 | x | x | 20,7 |
| 199,92 | 501,50 | x | x | x | x | x | x | |
| 2 | 39970,00 | 251503,56 | x | x | x | x | x | x |
;
.
Получено уравнение регрессии: 
.
С увеличением средняя заработная плата и выплаты социального характера на 1 руб., то потребительские расходы в расчете на душу населения возрастает в среднем на 0,33 руб.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
Тесноту связи оценивают с помощью показателей корреляции и детерминации:
.
Коэффициент детерминации
Это означает, что 69% вариации потребительские расходы в расчете на душу населения объясняется вариацией факторов средняя заработная плата и выплаты социального характера.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи факторов с результатом.
Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%. Формула для расчета коэффициента эластичности имеет вид:
.
Таким образом, изменение средней заработной платы и выплат социального характера на 1 % приведет к увеличению потребительских расходов в расчете на душу населения на 0,615 %.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
Качество уравнений оцените с помощью средней ошибки аппроксимации:
= 20,7%
Качество построенной модели оценивается как плохое, так как превышает 8 – 10 %.
6. Оцените с помощью F - критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп.4,5 и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование.
Оценим качество уравнения регрессии в целом с помощью 
-критерия Фишера. Сосчитаем фактическое значение - критерия:
.
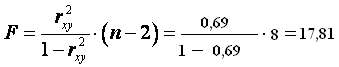Табличное значение (k1
=1, k2
=8 
) Fтабл.
=5,32. Так как 
, то признается статистическая значимость уравнения в целом.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитаем 
- критерий Стьюдента и доверительные интервалы каждого из показателей. Рассчитаем случайные ошибки параметров линейной регрессии и коэффициента корреляции
:
,
,
.
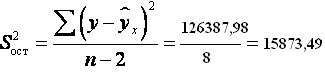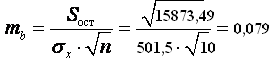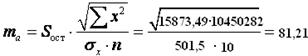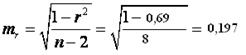Фактические значения - статистик:
.
Табличное значение - критерия Стьюдента при и tтабл.
=2,306. Так как 
, ta
t
табл.
и 
.
Рассчитаем доверительные интервалы для параметров регрессии 
и 
: 
и 
. Получим, что и 
.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 7 % от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости, а = 0,05.
Найдем прогнозное значение результативного фактора 
при значении признака-фактора, составляющем 107% от среднего уровня 
, т.е. найдем потребительские расходы в расчете на душу населения, если средняя заработная плата и выплаты социального характера составят 953,15 тыс. руб.
(тыс. руб.)
Значит, если средняя заработная плата и выплаты социального характера составят 953,15 тыс. руб., то потребительские расходы в расчете на душу населения будут 498,58 тыс. руб.
Найдем доверительный интервал прогноза. Ошибка прогноза
,
а доверительный интервал (
):
.
Т.е. прогноз является статистически не точным.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Из полученных результатов я вижу, что с увеличением средняя заработная плата и выплаты социального характера на 1 руб., то потребительские расходы в расчете на душу населения возрастает в среднем на 0,33 руб. При оценки тесноты связи с помощью показателя детерминации я выявил, что 69% вариации потребительские расходы в расчете на душу населения объясняется вариацией факторов средняя заработная плата и выплаты социального характера. С помощью коэффициент эластичности я определил, что изменение средней заработной платы и выплат социального характера на 1 % приведет к увеличению потребительских расходов в расчете на душу населения на 0,615 %. С увеличится на 7 %заработной платы и выплаты социального характера, потребительские расходы в расчете на душу населения будут равны 498,58 тыс. руб., но этот прогноз является статистически не точным.
Задача 8
По группе 10 заводов, производящих однородную продукцию, получено уравнение регрессии себестоимости единицы продукции у (тыс. руб.) от уровня технической оснащенности х (тыс. руб.):
у = 20 + 
. Доля остаточной дисперсии в общей составила 0,19
Задание:
Определите:
а) коэффициент эластичности, предполагая, что стоимость активных производственных фондов составляет 200 тыс. руб.
б) индекс корреляции;
в) F- критерий Фишера. Сделайте выводы.
Решение:
а) коэффициент эластичности, предполагая, что стоимость активных производственных фондов составляет 200 тыс. руб.
х = 200 тыс. руб.
.
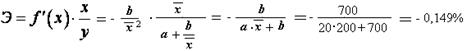
Таким образом, изменение технической оснащенности на 1% приведет к снижению себестоимости единицы продукции на 0,149 %.
б) индекс корреляции:
Уравнение регрессии:
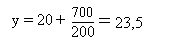
= 23,5/10 = 2,35 
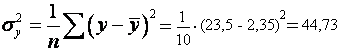
Это означает, что 99,6 % вариации себестоимости единицы продукции объясняется вариацией уровня технической оснащенности на долю прочих факторов приходится лишь 0,40%.
в) F - критерий Фишера. Сделайте выводы.
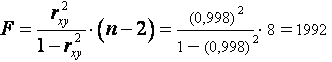
Fтабл. = 4,46
Fтабл. Fфакт ; Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений.
Задача 13
По заводам, выпускающим продукцию А, изучается зависимость потребления электроэнергии У (тыс. кВт. Ч) от производства продукции - Х1 (тыс.ед.) и уровня механизации труда – Х2 (%). Данные приведены в табл.4.2.
Задание
1. Постройте уравнение множественной регрессии в стандартизованном и натуральном масштабах.
2. Определите показатели частной и множественной корреляции.
3.Найдите частные коэффициенты эластичности и сравните их с Бэтта коэффициентами.
4. Рассчитайте общие и частные F – критерии Фишера.
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции | |
| Y | 1050 | 28 | ryx1 | 0.78 |
| X1 | 425 | 44 | ryx2 | 0.44 |
| X2 | 42.0 | 19 | rx1x2 | 0.39 |
Решение:
1. Постройте уравнение множественной регрессии в стандартизованном и натуральном масштабах.
Линейное уравнение множественной регрессии у от х1 и х2 имеет вид:
.
Для расчета его параметров применим метод стандартизации переменных, построим искомое уравнение в стандартизованном масштабе:
Расчет - коэффициентов выполним по формулам:
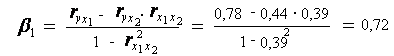
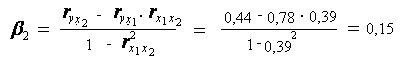
Т.е. уравнение будет выглядеть следующим образом:
.
Для построения уравнения в естественной форме рассчитаем b 1 и b 2 ,используя формулы для перехода от к b .
Значение a определим из соотношения:
2. Определите показатели частной и множественной корреляции.
Линейные коэффициенты частной корреляции здесь рассчитываются по рекуррентной формуле:
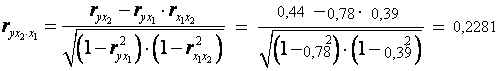
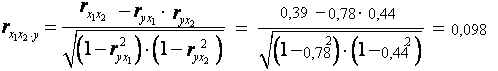
Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за слабой межфакторной связи (rx 1 x 2 =0,39) коэффициенты парной и частной корреляции отличаются значительно.
Растет линейного коэффициента множественной корреляции выполним с использованием коэффициентов и 
:
Зависимость у от х1 и х2 характеризуется как тесная, в которой 63 % вариации потребления электроэнергии определяется вариацией учетных в модели факторов: производства продукции и уровня механизации труда. Прочие факторы, не включенные в модель, составляют соответственно 37 % от общей вариации y .
3.Найдите частные коэффициенты эластичности и сравните их с Бэтта коэффициентами.
Для характеристики относительной силы влияния х1 и х2 на y рассчитаем средние коэффициенты эластичности:
С увеличением производства продукции на 1 % от его среднего потребления электроэнергии возрастает на 0,29 % от своего среднего уровня; при повышении среднего уровня механизации труда на 1 % среднее потребления электроэнергии увеличивается на 0,006% от своего среднего уровня. Очевидно, что сила влияния производства продукции на среднее потребление электроэнергии оказалась больше, чем сила влияния среднего уровня механизации труда.
4. Рассчитайте общие и частные F – критерии Фишера.
Общий F -критерий проверяет гипотезу H 0 о статистической значимости уравнения регрессии и показателя тесноты связи (R2 = 0):
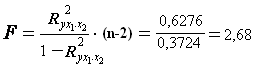
F табл. = 9,55
Сравнивая F табл. и F факт. , приходим к выводу о необходимости не отклонять гипотезу H 0 и признается статистическая незначимость, ненадежность уравнения регрессии.
Частные F -критерий – F х1. и F х2 оценивают статистическую значимость присутствия факторов х 1 и х 2 в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т.е. F х1 оценивает целесообразность включения в уравнение фактора х 1 после того, как в него был включен фактор х 2 . Соответственно F х2 указывает на целесообразность включения в модель фактора х 2 после фактора х 1.
Низкое значение F х2 (меньше 1) свидетельствует о статистической незначимости прироста r 2 yx 1 за счет включения в модель фактора х 2 после фактора х 1. следовательно, подтверждается нулевая гипотеза H 0 о нецелесообразности включения в модель фактора х 2.
Задача 21
Модель денежного и товарного рынков:
Rt = a1 + b12 Yt + b14 Mt + e1 , (функция денежного рынка);
Yt = a2 + b21 Rt + b23 It + b25 Gt + e2 ( функция товарного рынка);
It = a3 + b31 Rt + e3 (функция инвестиций),
где R- процентные ставки;
Y- реальный ВВП;
M- денежная масса;
I- внутренние инвестиции;
G- реальные государственные расходы.
Решение:
Rt
= a1
+ b12
Yt
+ b14
Mt
+ e1
,
Yt = a2 + b21 Rt + b23 It + b25 Gt + e2
It = a3 + b31 Rt + e3
Сt = Yt + It + Gt
Модель представляет собой систему одновременных уравнений. Проверим каждое ее уравнение на идентификацию.
Модель включает четыре эндогенные переменные (Rt
, Yt
, It
, Сt
) и две предопределенные переменные (
и 
).
Проверим необходимое условие идентификации для каждого из уравнений модели.
Первое уравнение:
Rt = a1 + b12 Yt + b14 Mt + e1 .
Это уравнение содержит две эндогенные переменные 
и 
и одну предопределенную переменную . Таким образом,
,
т.е. выполняется условие 
. Уравнение сверхидентифицируемо.
Второе уравнение:
Yt = a2 + b21 Rt + b23 It + b25 Gt + e2 .
Оно включает три эндогенные переменные Yt , It и Rt и одну предопределенную переменную Gt . Выполняется условие
.
Уравнение идентифицируемо.
Третье уравнение:
It = a3 + b31 Rt + e3 .
Оно включает две эндогенные переменные It и Rt . Выполняется условие
.
Уравнение идентифицируемо.
Четвертое уравнение:
Сt = Yt + It + Gt .
Оно представляет собой тождество, параметры которого известны. Необходимости в идентификации нет.
Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.
|
 |
Rt | |
|
|
|
| I уравнение | 0 | 0 | –1 | b12 | b14 | 0 |
| II уравнение | 0 | b23 |  |
–1 | 0 | b25 |
| III уравнение | 0 | –1 | b31 | 0 | 0 | 0 |
| Тождество | –1 | 1 | 0 | 1 | 0 | 1 |
В соответствии с достаточным условием идентификации ранг матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, должен быть равен числу эндогенных переменных модели без одного.
Первое уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
|
Rt | |
|
|
| II уравнение | b23 |  |
–1 | b25 |
| III уравнение | –1 | b31 | 0 | 0 |
| Тождество | 1 | 0 | 1 | 1 |
Ранг данной матрицы равен трем, так как определитель квадратной подматрицы 
не равен нулю:
.
Достаточное условие идентификации для данного уравнения выполняется.
Второе уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
 |
 |
Rt |  |
 |
 |
|
| I уравнение | 0 | 0 | –1 | b12 | b14 | 0 |
| III уравнение | 0 | -1 | b31 | 0 | 0 | 0 |
| Тождество | –1 | 1 | 0 | 1 | 0 | 1 |
Ранг данной матрицы равен трем, так как определитель квадратной подматрицы не равен нулю:
.
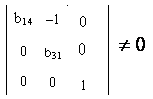Достаточное условие идентификации для данного уравнения выполняется.
Третье уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид
|
|
Rt | |
|
|
|
| I уравнение | 0 | 0 | –1 | b12 | b14 | 0 |
| II уравнение | 0 | b23 | |
–1 | 0 | b25 |
| Тождество | -1 | 1 | 0 | 1 | 0 | 1 |
Ранг данной матрицы равен трем, так как определитель квадратной подматрицы 
не равен нулю:
Достаточное условие идентификации для данного уравнения выполняется.
Таким образом, все уравнения модели сверхидентифицируемы. Приведенная форма модели в общем виде будет выглядеть следующим образом:
Rt = a1 + b11 Yt + b13 Mt + b15 Gt + b16 Gt + u1
Yt = a2 + b21 Rt + b23 It + b25 Gt + b26 Gt + u 2
It = a3 + b31 Rt + b33 It + b35 Gt + b36 Gt + u 3
Сt = a4 + b41 Rt + b43 It + b45 Gt + b46 Gt + u 4
Задача 26
Имеются данные об урожайности культур в хозяйствах области:
| Варианты | Показатели | Год | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 4 | Урожайность картофеля, ц/га | 63 | 64 | 69 | 81 | 84 | 96 | 106 | 109 |
Задание:
1. Обоснуйте выбор типа уравнения тренда.
2. Рассчитайте параметры уравнения тренда.
3.Дайте прогноз урожайности культур на следующий год.
Решение:
1. Обоснуйте выбор типа уравнения тренда.
Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравнивание временного ряда . Для этого применяют следующие функции:
- линейная 
- гипербола 
- экспонента 
- степенная функция 
- парабола второго и более высоких порядков 
Параметры трендов определяются обычными МНК, в качестве независимой переменной выступает время t=1,2,…,n, а в качестве зависимой переменной – фактические уровни временного ряда yt
. Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации 
.
Сравним значения R 2 по разным уровням трендов:
Полиномиальный 6-й степени - R 2 = 0,994
Экспоненциальный - R 2 = 0,975
Линейный - R 2 = 0,970
Степенной - R 2 = 0,864
Логарифмический - R 2 = 0,829
Исходный данные лучше всего описывает полином 6-й степени. Следовательно, для расчета прогнозных значений следует использовать полиномиальное уравнение.
2. Рассчитайте параметры уравнения тренда.
y = - 0,012*531441 + 0,292*59049 – 2,573*6561 +10,34*729 – 17,17*81 + 9,936*9 + 62,25 =
= - 6377,292 + 17242,308 – 16881,453 + 7537,86 - 1390,77 + 89,424 + 62,25 = 282,327
3.Дайте прогноз урожайности культур на следующий год.
Урожайность картофеля, ц/га в 9-ом году приблизительно будет 282 ц/га.