Расчет коэффициентов активности. Личный опыт
СОДЕРЖАНИЕ: О расчетах коэффициента активности растворов электролитов..
Не так давно я вплотную столкнулся с расчетами коэффициента активности растворов электролитов. Нельзя сказать, что раньше я никогда не производил таких расчетов, однако сейчас у меня возникли некоторые вопросы, связанные с расчетами в области высоких концентраций.
Известно, что до ионной силы 0,01М коэффициент активности (f) хорошо описывается расширенной формулой Дебая-Хюккеля:
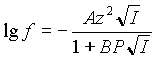 |
(1) |
где z - заряд иона;
I - ионная сила раствора;
P - параметр Килланда, зависящий от размера иона;
A = 0,509 при 250 С ;
B = 0,328 при 250 С .
Ионная сила раствора равна
| (2) |
где Ci - концентрация ионов одного вида в исследуемом растворе.
Для области большей ионной силы, самой распространенной является следующая формула:
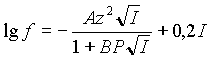 . . |
(3) |
Эта формула предполагает увеличение коэффициента активности после некоего значения ионной силы.
Большинство исследователей предпочитают в своих работах не упоминать об условиях, при которых следует от формулы (1) переходить к формуле (3). В связи с этим я предпринял собственные исследования, благо в моем распоряжении была программа IonCalc ( Программу можно получить здесь.).
Поскольку я располагал справочными данными (Краткий химический справочник В.А.Рабиновича и З.Я.Хавина, изд. Химия,1977г.) об экспериментально полученных значениях коэффициента активности, то работа состояла в сопоставлении этих данных с расчет ными. Расчеты я производил по формуле (1), так как применение формулы (3) только усугубляло расхождение между экспериментальными и расчетными данными.
В справочнике приведены экспериментально полученные данные о среднем коэффициенте активности растворов солей. Средний коэффициент активности составляют коэффициенты активности аниона и катиона следующим образом:
f ср m+n = fM m + fA n , где
fM иfA - коэффициенты активности катиона и аниона:
m и n - стехиометрические коэффициенты исследуемой соли Mm An .
Если распоряжаться этой формулой, то можно легко рассчитать средний коэффициент активности и сравнить его с экспериментальным.
Проведенные мной расчеты представлены в таблице, которая содержит сведения об относительной разнице в процентах между экспериментальными и расчетными данными. Относительная погрешность представлена в двух видах: среднеарифметическая величина погрешности (первое число) и максимальная погрешность в серии расчетов (второе число).
Таблица 1.*)
| I, M | 0,1 | 0,2 | 0,3 | 0,4 | 0,6 | 0,8 |
| MA 1) | 1,8/2,8 | 3,6/5,9 | - | 7,2/10 | - | - |
| MA2 2) | - | - | 2,8/5 | - | 5,8/7,5 | - |
| M2 A 3) | - | - | 3,8/5,5 | - | 5,9/11 | - |
| MSO4 4) | - | - | - | - | - | 76/91 |
| LaCl3 | - | - | - | - | 16 | - |
| H3 PO4 | - | - | - | - | 16 | - |
1) AgNO3 , HCl, HNO3 , KBr, KCl, KOH, NaCl, NaOH, NH4 Cl, NaCH3 COO, NaNO3 , KNO3 .
2) BaCl2 , CaCl2 , FeCl2 , MgBr2 , MgCl2 , Ca(NO3 )2 , Co(NO3 )2 , Cu(NO3 )2 .
3) K2 CrO4 , K2 SO4 , Na2 CrO4 , (NH4 )2 SO4 , Na2 SO4 , Na2 CO3 , K2 CO3 .
4) ZnSO4 , MgSO4 , MnSO4 , Cu SO4 .
Расчеты показывают, что для ионной силы в 0,3М максимальная погрешность составляет 5-6%.
Необъясненным остается тот факт, что коэффициент активности сульфатов двухзарядных металлов очень высок в сравнении с экспериментальными данными. Также высок средний коэффициент активности серной кислоты. Он составляет 0,266 для раствора с ионной силой 0,3 М, в то время как расчеты предоставляют величину 0,517.