Расчет показателей корреляционного, дисперсионного анализа
СОДЕРЖАНИЕ: Расчет матрицы выборочных парных коэффициентов корреляции при помощи пакета анализа программы Excel. Однофакторный и двухфакторный дисперсионный анализ. Построение регрессионной модели. Модальный интервал по значению числа видов производимой продукции.Задача 1. Корреляционный анализ
Исследовано функционирование некоторого предприятия торговли в течение n месяцев. Необходимо проанализировать наличие предполагаемой зависимости между: расходами предприятия на рекламу и продвижение товаров на рынок ![]() ,
,![]() (в тыс. грн); расходами на обучение и повышение квалификации персонала Yi
,
(в тыс. грн); расходами на обучение и повышение квалификации персонала Yi
, ![]() (в тыс. грн.); объемом товарооборота предприятия торговли Ui
,
(в тыс. грн.); объемом товарооборота предприятия торговли Ui
, ![]() (в млн. грн.); прибылью предприятия Zi
,
(в млн. грн.); прибылью предприятия Zi
, ![]() (в тыс. грн.).
(в тыс. грн.).
| X | Y | U | Z |
| 82 | 101 | 48 | 34 |
| 100 | 106 | 52 | 24 |
| 85 | 66 | 51 | 36 |
| 85 | 80 | 47 | 33 |
| 102 | 71 | 49 | 23 |
| 102 | 80 | 54 | 24 |
| 85 | 119 | 46 | 35 |
| 88 | 66 | 49 | 30 |
| 90 | 84 | 50 | 30 |
| 84 | 94 | 46 | 33 |
| 83 | 73 | 47 | 32 |
| 87 | 59 | 47 | 31 |
| 102 | 79 | 52 | 24 |
| 80 | 116 | 44 | 36 |
| 80 | 103 | 48 | 33 |
| 96 | 76 | 52 | 27 |
| 95 | 89 | 52 | 27 |
| 81 | 66 | 45 | 34 |
Провести предварительный анализ (описательную статистику) исследуемых компонентов многомерной случайной величины
Для всех пар случайных величин построить диаграммы рассеивания (корреляционные поля).
Рассчитать матрицу выборочных парных коэффициентов корреляции. Сделать выводы о степени тесноты и тенденции связи между парами компонентов исследуемого многомерного признака в терминах решаемой прикладной задачи.
Проверить гипотезу об отсутствии корреляционной связи между двумя компонентами случайной величины (X,Z).
Построить доверительные интервалы для двух парных коэффициентов корреляции при р=0.95 (X,Z;Y,Z).
Исключив из рассмотрения случайную величину, не зависящую от других, для оставшихся случайных величин рассчитать матрицу частных коэффициентов корреляции.
Рассчитать парные ранговые коэффициенты корреляции Спирмена и Кендалла для двух компонентов многомерной случайной величины (U,Y).
Рассчитать корреляционные отношения между случайными величинами, для которых можно предположить наличие нелинейной связи.
Рассчитать коэффициент конкордации для трех случайных величин, между которыми на основе проведенного анализа можно предположить наличие статистической связи.
Проверить гипотезу о статистической значимости исследуемой множественной связи.
В терминах решаемой прикладной задачи дать содержательную интерпретацию результатов для каждого из пунктов.
РЕШЕНИЕ
1. Построим диаграммы рассеивания
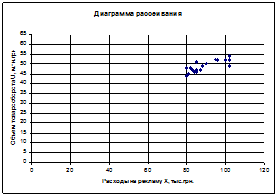
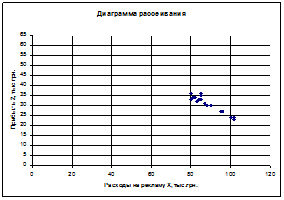
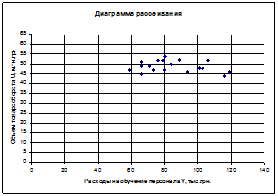
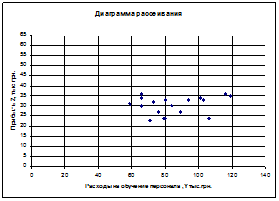
2. Рассчитаем матрицу выборочных парных коэффициентов корреляции при помощи пакета анализа программы Excel:
| U | X | Y | |
| U | 1 | ||
| X | 0,80766 | 1 | |
| Y | -0,3689 | -0,19614 | 1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, т.е. объем товарооборота предприятия торговли имеет сильную прямую связь с расходами предприятия на рекламу и продвижение товаров на рынок (0,40,811) и слабую обратную связь с расходами на обучение и повышение квалификации персонала (0,370,4). Мультиколлинеарность отсутствует, т.к. коэффициент парной корреляции равен -0,196, что не превышает значения 0,7-0,8.
| Z | X | Y | |
| Z | 1 | ||
| X | -0,95998 | 1 | |
| Y | 0,215933 | -0,19614 | 1 |
Анализ полученных коэффициентов парной корреляции показывает, что зависимая переменная, т.е. прибыль предприятия торговли имеет сильную обратную связь с расходами предприятия на рекламу и продвижение товаров на рынок (0,40,961) и слабую прямую связь с расходами на обучение и повышение квалификации персонала (0,220,4). Мультиколлинеарность отсутствует, т.к. коэффициент парной корреляции равен -0,196, что не превышает значения 0,7-0,8.
3. Проверить гипотезу об отсутствии корреляционной связи между двумя компонентами случайной величины (X,Z):
В предыдущем пункте проверка гипотезы об отсутствии корреляционной связи между расходами предприятия на рекламу и продвижение товаров на рынок и прибылью предприятия была опровергнута, т.к. проверка коэффициентов парной корреляции показывает, что зависимая переменная, т.е. прибыль предприятия торговли имеет сильную обратную связь с расходами предприятия на рекламу и продвижение товаров на рынок (0,40,961).
4. Построить доверительные интервалы для двух парных коэффициентов корреляции при р=0.95 (X,Z;Y,Z)
Полагая доверительную вероятность р = 0,95 т. е. вероятность, с которой гарантируются результаты, равной 0,95, находим соответствующее ей значение критерия Стьюдента t, равное 2,1009. Воспользовавшись формулой средней квадратической ошибки, где вместо р возьмем рассчитанный выборочный коэффициент корреляции r, получим значение для средней квадратической ошибки X,Z: р = 0,95; r = - 0,96
Поскольку tr = 2,1009 х 0,018 = 0,0388 верхняя и нижняя границы равны соответственно -0,9212 и -0,9988. Другими словами, с вероятностью 0,95 коэффициент корреляции данной совокупности находится в пределах от -0,9212 до -0,9988. Y,Z: р = 0,95; r = 0,216
Поскольку tr = 2,1009 х 0,22 = 0,47 верхняя и нижняя границы равны соответственно 0,69 и -0,25. Другими словами, с вероятностью 0,95 коэффициент корреляции данной совокупности находится в пределах от -0,25 до 0,69.
6. Рассчитать парные ранговые коэффициенты корреляции Спирмена и Кендалла для двух компонентов многомерной случайной величины (U,Y).
Запишем ранги:
| U | 48 | 52 | 51 | 47 | 49 | 54 | 46 | 49 | 50 | 46 | 47 | 47 | 52 | 44 | 48 | 52 | 52 | 45 |
| № Z | 11 | 5 | 6 | 14 | 9 | 1 | 16 | 8 | 7 | 15 | 13 | 12 | 4 | 18 | 10 | 3 | 2 | 17 |
| № X | 15 | 4 | 12 | 11 | 3 | 2 | 10 | 8 | 7 | 13 | 14 | 9 | 1 | 18 | 17 | 5 | 6 | 16 |
| -4 | 1 | -6 | 3 | 6 | -1 | 6 | 0 | 0 | 2 | -1 | 3 | 3 | 0 | -7 | -2 | -4 | 1 | |
| 16 | 1 | 36 | 9 | 36 | 1 | 36 | 0 | 0 | 4 | 1 | 9 | 9 | 0 | 49 | 4 | 16 | 1 |
![]() = 228
= 228
Тогда критерий Спирмена равен:
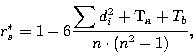
r = 0,765, это больше табличного значения критерия, значит корреляция достоверно отличается от 0.
Критерий Кендалла:
![]()
r = 4*153/(18*17) – 1 = -0,5
Значит между объемом товарооборота предприятия торговли и расходами предприятия на рекламу и продвижение товаров на рынок существует обратная средней тесноты связь.
| Y | 101 | 106 | 66 | 80 | 71 | 80 | 119 | 66 | 84 | 94 | 73 | 59 | 79 | 116 | 103 | 76 | 89 | 66 |
| Z | 4 | 15 | 1 | 6 | 18 | 16 | 3 | 11 | 12 | 7 | 9 | 10 | 17 | 2 | 8 | 13 | 14 | 5 |
| X | 15 | 4 | 10 | 11 | 1 | 2 | 12 | 8 | 7 | 13 | 14 | 9 | 3 | 17 | 18 | 5 | 6 | 16 |
| -11 | 11 | -9 | -5 | 17 | 14 | -9 | 3 | 5 | -6 | -5 | 1 | 14 | -15 | -10 | 8 | 8 | -11 | |
| 121 | 121 | 81 | 25 | 289 | 196 | 81 | 9 | 25 | 36 | 25 | 1 | 196 | 225 | 100 | 64 | 64 | 121 |
![]() = 1780
= 1780
Тогда критерий Спирмена равен:
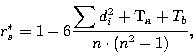
r = -0,837, это значит корреляция недостоверна. Значит между объемом товарооборота предприятия торговли и расходами на обучение и повышение квалификации персонала не существует связи.
7. Рассчитаем корреляционные отношения между случайными величинами, для которых можно предположить наличие нелинейной связи: расходами предприятия на рекламу и продвижение товаров на рынок и объемом товарооборота предприятия торговли; расходами предприятия на рекламу и продвижение товаров на рынок и прибылью предприятия.
Коэффициенты корреляции:
Rxu = 0,8
Rxz = -0,96
8. Рассчитаем коэффициент конкордации для расходов предприятия на рекламу и продвижение товаров на рынок, объемом товарооборота предприятия торговли и продвижение товаров на рынок и прибылью предприятия, между которыми на основе проведенного анализа можно предположить наличие статистической связи
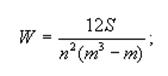
W = 0.88 – значит согласованность показателей стремиться к полной.
После проведении анализа можно сделать следующие выводы:
- объем товарооборота предприятия торговли имеет сильную прямую связь с расходами предприятия на рекламу и продвижение товаров на рынок (0,40,811) и слабую обратную связь с расходами на обучение и повышение квалификации персонала (0,370,4);
- . прибыль предприятия торговли имеет сильную обратную связь с расходами предприятия на рекламу и продвижение товаров на рынок (0,40,961) и слабую прямую связь с расходами на обучение и повышение квалификации персонала (0,220,4);
- между объемом товарооборота предприятия торговли и расходами предприятия на рекламу и продвижение товаров на рынок существует обратная средней тесноты связь;
- Rxu = 0,8 корреляция между расходами предприятия на рекламу и продвижение товаров на рынок и объемом товарооборота предприятия торговли;
Rxz = -0,96 корреляция расходами предприятия на рекламу и продвижение товаров на рынок и прибылью предприятия.
Задача 2. Однофакторный дисперсионный анализ
При уровне значимости a=0.05 определите статистическую достоверность влияния фактора А на динамику величины Х.
| № испытания | A1 | A2 | A3 | A4 |
| 1 | 2 | 2 | 6 | 7 |
| 2 | 0 | 13 | 8 | 11 |
| 3 | 14 | 13 | 10 | 2 |
| 4 | 11 | 5 | 9 | 5 |
| 5 | 1 | 12 | 4 | 6 |
| 6 | 7 | 4 | 8 |
РЕШЕНИЕ
Число выборок m=6, значения во всех выборках n=22
| № испытания | A1 | A2 | A3 | A4 | n | |
| 1 | 2 | 2 | 6 | 7 | 17 | 4 |
| 2 | 0 | 13 | 8 | 11 | 32 | 3 |
| 3 | 14 | 13 | 10 | 2 | 39 | 4 |
| 4 | 11 | 5 | 9 | 5 | 30 | 4 |
| 5 | 1 | 12 | 4 | 6 | 23 | 4 |
| 6 | 7 | 4 | 8 | 19 | 3 |
Выборочное среднее:
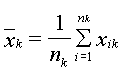
Сумма квадратов отклонений выборочных средних ![]() от общего среднего
от общего среднего ![]() (сумма квадратов отклонений между группами):
(сумма квадратов отклонений между группами):
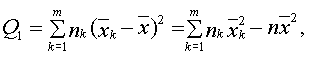
Сумма квадратов отклонений наблюдаемых значений ![]() от выборочной средней
от выборочной средней ![]() (сумма квадратов отклонений внутри групп):
(сумма квадратов отклонений внутри групп):
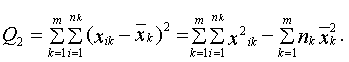
Общая сумма квадратов отклонений наблюдаемых значений ![]() от общего среднего
от общего среднего
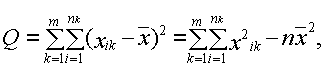
| № | А ср. | А ср.2 | А ср.2 * n |
| 1 | 4,25 | 18,0625 | 72,25 |
| 2 | 10,66667 | 113,7778 | 341,3333 |
| 3 | 9,75 | 95,0625 | 380,25 |
| 4 | 7,5 | 56,25 | 225 |
| 5 | 5,75 | 33,0625 | 132,25 |
| 6 | 6,333333 | 40,11111 | 120,3333 |
| 7,272727 | 1271,417 |
Тогда Q = 330,36
Q1 = 107,18
Q2 = Q – Q1 = 222,58
В качестве критерия необходимо воспользоваться критерием Фишера:
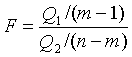
F = 1,549
Табличное значение критерия Фишера для заданном уровне значимости 0,05 равен 3,8564.
Так как расчетное значение критерия Фишера меньше табличного, нет оснований считать, что независимый фактор оказывает влияние на разброс средних значений.
Задача 3. Двухфакторный дисперсионный анализ
При уровне значимости a=0.05 определите статистическую достоверность влияния фактора А и фактора В на динамику величины Х.
| B1 | B2 | B3 | B4 | |
| A1 | 3 | 3 | 12 | 20 |
| A2 | 7 | 10 | 18 | 7 |
| A3 | 7 | 15 | 6 | 17 |
| A4 | 5 | 18 | 0 | 18 |
| A5 | 8 | 10 | 8 | 9 |
РЕШЕНИЕ
При двухфакторном дисперсионном анализе изучается влияние, которое оказывают два качественных признака (факторы A и B ) на некоторый количественный результат (отклик). Весьма типична ситуация, когда второй фактор (фактор B) является мешающим: он включается в рассмотрение по той причине, что мешает обнаружить и оценить влияние фактора A.
Пусть фактор A имеет k уровней A1 , ..., Ak , а фактор B - n уровней B1 ,...,Bn . Предполагается, что измеряемая величина x есть результат действия факторов A и B и случайной составляющей e :
![]()
Принимается аддитивная и независимая модель действия факторов:
![]() причем
причем
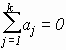 ,
, ![]()
Последние два условия всегда можно выполнить смещением величин aj и bi и изменением величины c; величины aj и bi называются вкладами факторов.
Проведем двухфакторный дисперсионный анализ при помощи пакета анализа программы Excel:
| ИТОГИ | Счет | Сумма | Среднее | Дисперсия |
| A1 | 4 | 38 | 9,5 | 67 |
| A2 | 4 | 42 | 10,5 | 27 |
| A3 | 4 | 45 | 11,25 | 30,91666667 |
| A4 | 4 | 41 | 10,25 | 84,25 |
| A5 | 4 | 35 | 8,75 | 0,916666667 |
| B1 | 5 | 30 | 6 | 4 |
| B2 | 5 | 56 | 11,2 | 32,7 |
| B3 | 5 | 44 | 8,8 | 45,2 |
| B4 | 5 | 71 | 14,2 | 33,7 |
| Дисперсионный анализ | ||||||
Источник вариации |
Сумма квадратов отклонений | Степени свободы | Среднеквадратическое отклонение | Отношение ср.кв.откл. фактора к ср.кв.откл. погрешности | P-Значение | F критическое |
| А | 14,7 | 4 | 3,675 | 0,0985 | 0,9809 | 3,259 |
| В | 182,55 | 3 | 60,85 | 1,631 | 0,2343 | 3,49 |
| Погрешность | 447,7 | 12 | 37,308 | |||
| Итого | 644,95 | 19 | ||||
Так как расчетное значение 0,98 и 0,23 больше заданного уровня значимости независимый фактор оказывает существенное влияние на разброс средних значений.
Задача 4. Регрессионный анализ
Построить регрессионную модель и провести полный регрессионный анализ.
| X 5.4 2.7 3.1 8.1 5.3 |
| Y 0.0 -1.3 -1.1 1.4 -0.6 |
РЕШЕНИЕ
Построим диаграмму и добавим линию тренда для того чтобы определить коэффициенты регрессия и значение достоверности аппроксимации:
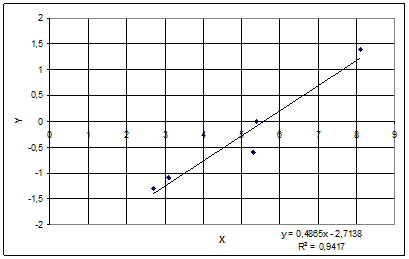
Дальнейшее исследование выполним при помощи пакета анализа программы Excel:
| ВЫВОД ИТОГОВ | |
| Регрессионная статистика | |
| Множественный R | 0,97 |
| R-квадрат | 0,94 |
| Нормированный R-квадрат | 0,91 |
| Стандартная ошибка | 0,36 |
| Наблюдения | 4,00 |
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 1,00 | 4,31 | 4,31 | 32,55 | 0,03 |
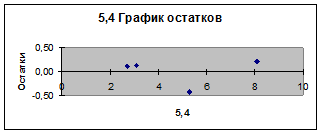
| Остаток | 2,00 | 0,27 | 0,13 | ||
| Итого | 3,00 | 4,58 |
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
| Y-пересечение | -2,72 | 0,45 | -6,11 | 0,03 |
| 5,4 | 0,48 | 0,08 | 5,71 | 0,03 |
Уравнение регрессии полученное с помощью Excel, имеет вид:
у = 0,4865х – 2,7138
По данным регрессионного анализа можно сказать:
- т.к. коэффициент детерминации равен 0,94, то вариация результата на 94% объясняется вариацией факторов.
- F-критерий равен 32,55, его табличное значение 3,98. т.к. фактическое значение превышает табличное, то делаем вывод, что полученной уравнение регрессии статистически значимо.

Задание №5
Предприятия мясной промышленности сгруппированы по числу видов производимой колбасной продукции. По данным табл. 5 (за отчётный год) определить: а) модальное, медианное и среднее значение числа видов производимой продукции; б) среднюю в целом по совокупности предприятий энергоёмкость продукции; в) среднюю себестоимость 1 т колбасных изделий по совокупности предприятий.
Таблица 5
| Число видов производимой колбасной продукции | Число предприятий в группе | Суммарный объём выпуска колбасной продукции по группе предприятий, т | Средняя энергоёмкость 1 т продукции по группе предприятий, ГДж/ т | Средняя себестоимость 1 т продукции по группе предприятий, тыс. руб./ т |
| До 4 | 11 | 580 | 6,2 | 86 |
| 5 – 7 | 11 | 520 | 6,5 | 91 |
| 8 – 10 | 14 | 610 | 6,3 | 87 |
| 11 – 13 | 13 | 480 | 6,6 | 93 |
| 14 – 16 | 5 | 210 | 6,9 | 96 |
| 17 и более | 6 | 300 | 7,1 | 95 |
Решение:
Таблица 5.1
| Число видов производимой колбасной продукции | Число предприятий в группе | Накопленная частота | Закрытые интервалы группы | Середина интервала |
| До 4 | 11 | 11 | 1 - 4 | 2.5 |
| 5 – 7 | 11 | 22 | 5 – 7 | 6 |
| 8 – 10 | 14 | 36 | 8 – 10 | 9 |
| 11 – 13 | 13 | 49 | 11 – 13 | 12 |
| 14 – 16 | 5 | 54 | 14 – 16 | 15 |
| 17 и более | 6 | 60 | 17 - 19 | 18 |
| 60 |
Модой называется величина признака (вариант), которая чаще всего встречается в статистической совокупности. В вариационном ряду это будет значение показателя, имеющее наибольшую частоту.
Для интервального ряда распределения мода рассчитывается по следующей формуле
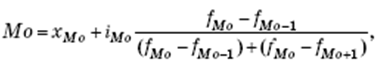
где xMo — нижняя граница модального интервала; iMo — величина модального интервала; fMo , fMo 1 , fMo +1 — частота модального, предшествующего модальному и последующего за модальным интервала.
Модальным интервалом по значению числа видов производимой продукции является интервал 8-10, т.к. наибольшее число предприятий (14) находится в данном интервале.
Мо = 8 + 2 · (14 – 11)/((14 – 11) + (14 – 13)) = 9,5
Наиболее часто встречающееся значение числа видов производимой продукции является 9,5.
Медианой называется варианта, которая находится в середине вариационного ряда по частоте. Медиана делит ряд пополам, по обе стороны от нее находится одинаковое количество единиц совокупности. Медиана показывает количественную границу варьирующего признака, которую достигла половина членов совокупности.
В интервальном ряду распределения медиана рассчитывается следующим образом
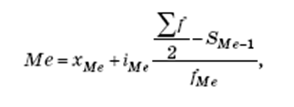
где xMo — нижняя граница медианного интервала;
iMo — величина медианного интервала;
SMe 1 — частота, накопленная до медианного интервала;
fMе — частота медианного интервала.
Для расчета медианы определяются накопленные частоты. Медианным является интервал, на который приходится половина предприятий, т.е. интервал 5 – 7.
Ме = 5 + 2 · (60/2 – 11)/11 = 8,45.
Половина предприятий выпускает 8,45 видов производимой продукции.
При определении средней величины в интервальном ряду с открытыми интервалами прежде всего необходимо закрыть интервалы.
Используем формулу средней арифметической взвешенной
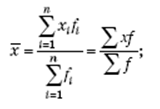
где x — значения (варианты) признака; n — число вариантов (число наблюдений), из которых рассчитывается средняя; f — статистический вес (число повторений значения признака).
Х = (2,5 · 11 + 6 · 11 + 9 · 14 + 12 · 13 + 15 · 5 + 18 · 6)/60 = 9,31
Таблица 5.2
| Число видов производимой колбасной продукции | Число предприятий в группе | Суммарный объём выпуска колбасной продукции по группе предприятий, Q, т | Средняя энергоёмкость 1 т продукции по группе предприятий, E, ГДж/ т |
Средняя себестоимость 1 т продукции по группе предприятий, С тыс. руб./ т | Q·E | Q·C |
| До 4 | 11 | 580 | 6,2 | 86 | 3596 | 49880 |
| 5 – 7 | 11 | 520 | 6,5 | 91 | 3380 | 47320 |
| 8 – 10 | 14 | 610 | 6,3 | 87 | 3843 | 53070 |
| 11 – 13 | 13 | 480 | 6,6 | 93 | 3168 | 44640 |
| 14 – 16 | 5 | 210 | 6,9 | 96 | 1449 | 20160 |
| 17 и более | 6 | 300 | 7,1 | 95 | 2130 | 28500 |
| 2700 | 17566 | 243570 |
При определении средней в целом по совокупности предприятий энергоёмкость продукции и средней себестоимости 1 т колбасных изделий по совокупности предприятий используем формулу средней арифметической взвешенной
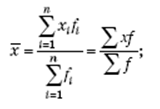
где x — значения (варианты) признака; n — число вариантов (число наблюдений), из которых рассчитывается средняя; f — статистический вес (число повторений значения признака).
Средняя в целом по совокупности предприятий энергоёмкость продукции
Еср = (580 · 6,2 + 520 · 6,5 + 610 · 6,3 + 480 · 6,6 + 210 · 6,9 + 300 · 7,1)/2700 = =6.505926 ГДж/ т.
Средняя себестоимость 1 т колбасных изделий по совокупности предприятий
Сср = (580 · 86 + 520 · 91 + 610 · 87 + 480 · 93 + 210 · 9,6 + 300 · 95)/2700 = =90.21111 тыс. руб./ т.
Задание №10
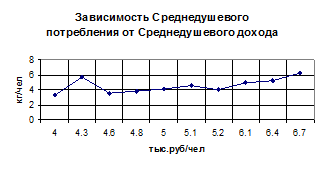
По данным табл. 10: 1) графически изобразить зависимость результирующего показателя от каждой факторной величины ; 2) построить уравнения парной регрессии результирующего показателя от каждого отдельного фактора; 3) рассчитать выровненные значения результирующего показателя по полученным уравнениям регрессии; 4) рассчитать характеристики тесноты (силы) корреляционной зависимости результата от каждого из факторов в отдельности и от совокупности обоих факторов. Сделать выводы по результатам расчётов.
Таблица 10
| Город | Среднедушевое потребление деликатесной мясной продукции в год, кг/ чел. | Среднегодовая цена продукции по городу, руб./кг | Среднедушевой доход одного жителя города за месяц, тыс. руб./ чел. |
| А | 3,5 | 215 | 4,6 |
| Б | 3,8 | 230 | 4,8 |
| В | 6,2 | 265 | 6,7 |
| Г | 4,6 | 205 | 5,1 |
| Д | 5,7 | 200 | 4,3 |
| Е | 4,1 | 220 | 5,0 |
| Ж | 3,3 | 225 | 4,0 |
| З | 4,9 | 230 | 6,1 |
| И | 5,2 | 250 | 6,4 |
| К | 4,0 | 245 | 5,2 |
Решение:
| Y | X | Z | Y-Yср | (Y-Yср)2 | Х-Хср | (х-хср)2 | Z-Zср | (Z-Zср)2 | (Y-Yср) * (Х-Хср) | (Y-Yср) * (Z-Zср) |
| 3.5 | 215 | 4.6 | -1.03 | 1.0609 | -13.5 | 182.25 | -0.62 | 0.3844 | 13.905 | 0.6386 |
| 3.8 | 230 | 4.8 | -0.73 | 0.5329 | 1.5 | 2.25 | -0.42 | 0.1764 | -1.095 | 0.3066 |
| 6.2 | 265 | 6.7 | 1.67 | 2.7889 | 36.5 | 1332.25 | 1.48 | 2.1904 | 60.955 | 2.4716 |
| 4.6 | 205 | 5.1 | 0.07 | 0.0049 | -23.5 | 552.25 | -0.12 | 0.0144 | -1.645 | -0.0084 |
| 5.7 | 200 | 4.3 | 1.17 | 1.3689 | -28.5 | 812.25 | -0.92 | 0.8464 | -33.345 | -1.0764 |
| 4.1 | 220 | 5 | -0.43 | 0.1849 | -8.5 | 72.25 | -0.22 | 0.0484 | 3.655 | 0.0946 |
| 3.3 | 225 | 4 | -1.23 | 1.5129 | -3.5 | 12.25 | -1.22 | 1.4884 | 4.305 | 1.5006 |
| 4.9 | 230 | 6.1 | 0.37 | 0.1369 | 1.5 | 2.25 | 0.88 | 0.7744 | 0.555 | 0.3256 |
| 5.2 | 250 | 6.4 | 0.67 | 0.4489 | 21.5 | 462.25 | 1.18 | 1.3924 | 14.405 | 0.7906 |
| 4 | 245 | 5.2 | -0.53 | 0.2809 | 16.5 | 272.25 | -0.02 | 0.0004 | -8.745 | 0.0106 |
| Сумма | ||||||||||
| 4.53 | 228.5 | 5.22 | -2.7E-15 | 8.321 | 0 | 3702.5 | -7.1E-15 | 7.316 | 52.95 | 5.054 |
Рассчитаем конечный вид уравнений прямолинейной регрессии по формуле
![]()
yx = 1.262 + 0.014x
yz = 0.924 + 0.69z
Из полученных уравнений рассчитаем выровненные значения результирующего показателя
Среднедушевое потребление деликатесной мясной продукции в год, кг/ чел. |
Среднегодовая цена продукции по городу, руб./кг | Среднедушевое потребление деликатесной мясной продукции в год, кг/ чел. | Среднедушевой доход одного жителя города за месяц, тыс. руб./ чел. |
| 4.337 | 215 | 4.102 | 4.6 |
| 4.551 | 230 | 4.240 | 4.8 |
| 5.052 | 265 | 5.552 | 6.7 |
| 4.194 | 205 | 4.447 | 5.1 |
| 4.122 | 200 | 3.894 | 4.3 |
| 4.408 | 220 | 4.378 | 5 |
| 4.480 | 225 | 3.687 | 4 |
| 4.551 | 230 | 5.138 | 6.1 |
| 4.837 | 250 | 5.345 | 6.4 |
| 4.766 | 245 | 4.516 | 5.2 |
Рассчитаем значение нормированного коэффициента корреляции по формуле:
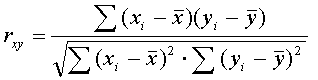
rxy = 0.301669
rzy = 0.647755
Общая классификация корреляционных связей
сильная, или тесная при коэффициенте корреляции r0,70;
средняя при 0,50r0,69;
умеренная при 0,30r0,49;
слабая при 0,20r0,29;
очень слабая при r0,19.
Следовательно, связь между Среднегодовой ценой продукции по городу и Среднедушевым потреблением деликатесной мясной продукции в год (rxy = 0,301669) умеренная.
Связь между Среднедушевым доход одного жителя города за месяц и Среднедушевым потреблением деликатесной мясной продукции в год (rzy = 0,647755) средняя.
Критическое значение коэффициента корреляции ккрит =0,72, так как рассчитанные значения меньше критического, предположение о том что зависимость достоверная ложно.
Задание №14
По данным табл. 14 определить: 1) основные параметры вариационного ряда (среднее арифметическое, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации), сделать вывод об однородности совокупности данных и следствии из него; 2) графически изобразить вариационный ряд и определить аналитический вид распределения частот (или частостей); 3) рассчитать теоретические частоты (частости) по предполагаемому аналитическому уравнению и построить полигон распределения теоретических частот (частостей) на предыдущем графике.
Таблица 14
| Количество поставщиков основного сырья на предприятие | Число предприятий |
| 1 | 4 |
| 2 | 6 |
| 3 | 10 |
| 4 | 12 |
| 5 | 13 |
| 6 | 11 |
| 8 | 7 |
| 9 | 8 |
| 11 | 5 |
| 14 | 4 |
Решение:
Среднее арифметическое рассчитаем по формуле среднего арифметического взвешенного:
![]()
Среднее линейное отклонение (средний модуль отклонения) от среднего арифметического. Среднее линейное отклонение рассчитывается по формуле:
![]()
Отклонение наблюдаемого значения (для каждого наблюдения) ai величины А от среднего арифметического: ai - a. Для определения дисперсии нормального закона распределения ошибок в этом случае пользуются формулой:
![]()
Среднеквадратическое отклонение показывает абсолютное отклонение измеренных значений от среднеарифметического. В соответствии с формулой для меры точности линейной комбинации средняя квадратическая ошибка среднего арифметического определяется по формуле:
![]()
Коэффициент вариации характеризует относительную меру отклонения измеренных значений от среднеарифметического:
![]()
| Количество поставщиков основного сырья на предприятие | Число предприятий | Частота | Накопленная частота | а-аср | (а-аср )2 | а*n | (а-аср )2 *n |
| 1 | 4 | 4 | 0.05 | -4.8 | 23.04 | 4 | 92.16 |
| 2 | 6 | 10 | 0.075 | -3.8 | 14.44 | 12 | 86.64 |
| 3 | 10 | 20 | 0.125 | -2.8 | 7.84 | 30 | 78.4 |
| 4 | 12 | 32 | 0.15 | -1.8 | 3.24 | 48 | 38.88 |
| 5 | 13 | 45 | 0.1625 | -0.8 | 0.64 | 65 | 8.32 |
| 6 | 11 | 56 | 0.1375 | 0.2 | 0.04 | 66 | 0.44 |
| 8 | 7 | 63 | 0.0875 | 2.2 | 4.84 | 56 | 33.88 |
| 9 | 8 | 71 | 0.1 | 3.2 | 10.24 | 72 | 81.92 |
| 11 | 5 | 76 | 0.0625 | 5.2 | 27.04 | 55 | 135.2 |
| 14 | 4 | 80 | 0.05 | 8.2 | 67.24 | 56 | 268.96 |
| Сумма | 80 | 1 | 464 | 824.8 |
Тогда используя формулы и предварительные расчеты определим основные параметры вариационного ряда:
| Среднее арифметическое | 5.8 |
| Среднее линейное отклонение | 3.3 |
| Дисперсия | 10.31 |
| Среднее квадратическое отклонение | 3.210918872 |
| Коэффициент вариации | 55.36% |
Проверка однородности совокупности осуществляется по коэффициенту вариации. Так как коэффициент вариации равен 55,36% (больше 33%) то совокупность неоднородна. Существует большой разброс данных или размера выборки мало.
Графически изобразим вариационный ряд:
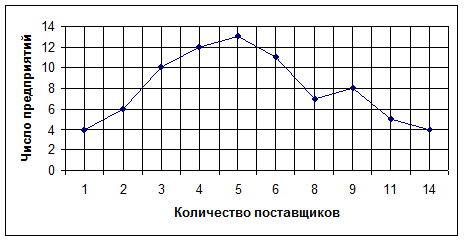
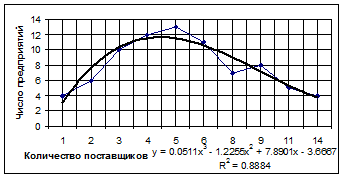
Аналитическое уравнение
y = 0.0511x3 - 1.2255x2 + 7.8901x - 3.6667
Рассчитаем теоретические частоты
| Количество поставщиков основного сырья на предприятие | Число предприятий |
| 1 | 3.049 |
| 2 | 7.6203 |
| 3 | 10.3538 |
| 4 | 11.5561 |
| 5 | 11.5338 |
| 6 | 10.5935 |
| 8 | 7.1853 |
| 9 | 5.3306 |
| 11 | 2.853 |
| 14 | 6.8151 |
Задание №20
По данным таблицы 20: 1) комплексно проанализировать сложившуюся динамику экономического показателя, рассчитав все его параметры; 2) построить сглаженный динамический ряд; 3) сделать простейшие прогнозы уровня ряда по выявленной тенденции.
Таблица 20
Экономический показатель |
Годы | ||||||||
| 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | |
| Экспорт продукции фирмы, тыс. $ | 800 | 800 | 802 | 800 | 803 | 808 | 810 | 809 | 812 |
Решение:

Абсолютный прирост — разность двух уровней временного ряда, один из которых (исследуемый) рассматривается как текущий, другой (с которым он сравнивается) как базисный. Если сравнивают каждый текущий уровень (yt или y(t)) с непосредственно ему предшествующим (yt-1) или y(t-1)), то получают цепные абсолютные приросты. Если сравнивают уровень yt с начальным уровнем ряда (y0) или иным уровнем, принятым за базу сравнения (yt), то получают базисные абсолютные приросты. Приросты выражаются либо в абсолютных величинах, либо в процентах, в единицах. Темп прироста (в других терминах — темп роста) — отношение прироста исследуемого показателя к соответствующему уровню временного ряда, принятому за базу сравнения:
![]()
в случае, когда ведется сравнение с предшествующим периодом, или
![]()
когда сравнивается конечный член ряда в n периодов (лет) с начальным. Темп роста (в других терминах — рост или индекс роста) — отношение одного уровня временного ряда к другому, взятому за базу сравнения; выражается в процентах либо в коэффициентах роста.
Цепные показатели:
| Год | Экспорт | Абсолютное изменение | Темп роста | Темп прироста | Абсолютное значение 1% прироста |
| 1998 | 800 | - | - | - | - |
| 1999 | 800 | 0 | 100 | 0 | 8 |
| 2000 | 802 | 2 | 100.25 | 0.25 | 8 |
| 2001 | 800 | -2 | 99.75062 | -0.24938 | 8.02 |
| 2002 | 803 | 3 | 100.375 | 0.375 | 8 |
| 2003 | 808 | 5 | 100.6227 | 0.622665 | 8.03 |
| 2004 | 810 | 2 | 100.2475 | 0.247525 | 8.08 |
| 2005 | 809 | -1 | 99.87654 | -0.12346 | 8.1 |
| 2006 | 812 | 3 | 100.3708 | 0.370828 | 8.09 |
Базовые показатели:
| Год | Экспорт | Абсолютное изменение | Темп роста | Темп прироста |
| 1998 | 800 | - | - | - |
| 1999 | 800 | 0 | 100 | 0 |
| 2000 | 802 | 2 | 100.25 | 0.25 |
| 2001 | 800 | -2 | 100 | 0 |
| 2002 | 803 | 3 | 100.375 | 0.375 |
| 2003 | 808 | 5 | 101 | 1 |
| 2004 | 810 | 2 | 101.25 | 1.25 |
| 2005 | 809 | -1 | 101.125 | 1.125 |
| 2006 | 812 | 3 | 101.5 | 1.5 |
Средний темп роста, %. Это средний коэффициент роста, который выражается в процентах:
![]()
Средний темп роста равен 100.1863%.
Средний темп прироста ![]() , %. Для расчета данного показателя первоначально определяется средний темп роста, который затем уменьшается на 100%. Его также можно определить, если уменьшить средний коэффициент роста на единицу:
, %. Для расчета данного показателя первоначально определяется средний темп роста, который затем уменьшается на 100%. Его также можно определить, если уменьшить средний коэффициент роста на единицу:
![]()
Средний темп прироста равен 0,1863%.
Построим сглаженный ряд динамики по методу скользящей средней.
Скользящая средняя - это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Если, предположим, продолжительность периода равна 3, то скользящие средние рассчитываются следующим образом:
![]()
![]()
![]()
Экономический показатель |
Годы | ||||||||
| 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | |
| Экспорт продукции фирмы, тыс. $ | 800 | 800 | 802 | 800 | 803 | 808 | 810 | 809 | 812 |
| Экспорт продукции фирмы, тыс. $ | - | 800.67 | 800.67 | 801.67 | 803.67 | 807.00 | 809.00 | 810.33 | - |
На основании среднего темпа роста сделаем простейшие прогнозы уровня ряда:
Экономический показатель |
Годы | ||||||||
| 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | |
| Экспорт продукции фирмы, тыс. $ | 812 | 813.51 | 815.03 | 816.55 | 818.07 | 819.59 | 821.12 | 822.65 | 824.18 |
Задание №25
По данным табл. 25:
1) определить индивидуальные индексы физического объема;
2) агрегатный индекс физического объема товарной продукции;
3) рассчитать индивидуальные и агрегатный индексы цен;
4) провести факторный анализ изменения объема товарной продукции.
Таблица 25
| Продукция | Объём производства за месяц, т | Отпускная цена предприятия, тыс. руб. / т | ||
| октябрь 2006 г. | ноябрь 2006 г. | октябрь 2006 г. | ноябрь 2006 г. | |
| А | 57 | 50 | 6,9 | 7,3 |
| Б | 69 | 61 | 8,1 | 8,2 |
| В | 80 | 66 | 7,2 | 7,5 |
| Г | 54 | 43 | 7,0 | 7,1 |
Решение:
Индекс физического объема продукции (ФОП) отражает изменение выпуска продукции. Индивидуальный индекс ФОП отражает изменение выпуска продукции одного вида и определяется по формуле
![]()
Агрегатный индекс ФОП (предложен Э. Ласпейресом) отражает изменение выпуска всей совокупности продукции, где индексируемой величиной является количество продукции q, а соизмерителем - цена р:
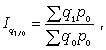
где q1 и q0 - количество выработанных единиц отдельных видов продукции соответственно в отчетном и базисном периодах; p0 - цена единицы продукции (отдельного вида) в базисном периоде.
Индивидуальный индекс цен характеризует изменение цен по одному виду продукции и определяется по формуле
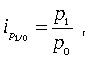
Агрегатный индекс цены (товарооборота) характеризует изменение общей стоимости продукции за счет изменения количества продукции и цен и определяется по формуле
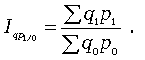
где p1 и p0 - цена единицы продукции данного вида в текущем и базисном периодах; q1 p1 и q0 p0 - стоимость продукции данного вида в текущем и базисном периодах.
| Продукция | Объём производства за месяц, т | Отпускная цена предприятия, | q0 p0 | q1 p1 | q1 p0 | ||
| тыс. руб. / т | |||||||
| октябрь 2006 г. | ноябрь 2006 г. | октябрь 2006 г. | ноябрь 2006 г. | ||||
| А | 57.00 | 50.00 | 6.90 | 7.30 | 393.30 | 365.00 | 345 |
| Б | 69.00 | 61.00 | 8.10 | 8.20 | 558.90 | 500.20 | 494.1 |
| В | 80.00 | 66.00 | 7.20 | 7.50 | 576.00 | 495.00 | 475.2 |
| Г | 54.00 | 43.00 | 7.00 | 7.10 | 378.00 | 305.30 | 301 |
| Сумма | 1906.20 | 1665.50 | 1615.3 | ||||
| Индивидуальный индекс физического объема продукции А | 0.88 |
| Индивидуальный индекс физического объема продукции Б | 0.88 |
| Индивидуальный индекс физического объема продукции В | 0.83 |
| Индивидуальный индекс физического объема продукции Г | 0.80 |
| Индивидуальный индекс цены продукции А | 1.06 |
| Индивидуальный индекс цены продукции Б | 1.01 |
| Индивидуальный индекс цены продукции В | 1.04 |
| Индивидуальный индекс цены продукции Г | 1.01 |
| Агрегатный индекс физического объема продукции | 0.85 |
| Агрегатный индекс цены | 0.87 |
Физический объем продукции (объем производства в неизменных ценах) по всем изделиям уменьшился на 15 %.
Цены в среднем снизились на 13%. Это связано с тем, что даже при том, что цены на продукцию повысились, что видно по индивидуальным индексам цен, произошло резкое снижения объемов производства.
Задание №30
По данным табл. 30 провести факторный анализ изменений прибыли фирмы.
Таблица 30
| Продукция | Объём производства за месяц, т | Отпускная цена предприятия, Тыс. руб. / т | Себестоимость 1 т продукции, тыс. руб. / т | |||
| октябрь 2006 г. | ноябрь 2006 г. |
октябрь 2006 г. |
ноябрь 2006 г. |
октябрь 2006 г. |
ноябрь 2006 г. |
|
| А | 57 | 50 | 6,9 | 7,3 | 5,8 | 5,9 |
| Б | 69 | 61 | 8,1 | 8,2 | 6,9 | 7,2 |
| В | 80 | 66 | 7,2 | 7,5 | 5,6 | 6,1 |
| Г | 54 | 43 | 7,0 | 7,1 | 6,7 | 6,9 |
Решение:
Индекс затрат на выпуск продукции (ЗВП), который отражает изменение затрат на производство и может быть как индивидуальным, так и агрегатным.
Индивидуальный индекс ЗВП отражает изменение затрат на производство одного вида и определяется по формуле
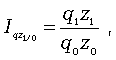
где z1 и z0 - себестоимость единицы продукции искомого вида в текущем и базисном периодах; q1 z1 и q0 z0 - суммы затрат на выпуск продукции искомого вида в текущем и базисном периодах.
Агрегатный индекс ЗВП характеризует изменение общей суммы затрат на выпуск продукции за счет изменения количества выработанной продукции и ее себестоимости и определяется по формуле
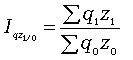
где q1 z1 и q0 z0 - затраты на выпуск продукции каждого вида соответственно в отчетном и базисном периодах.
| Продукция | Объём производства за месяц, т | Отпускная цена предприятия, тыс. руб./т | Себестоимость 1 т продукции, тыс. руб. / т | Прибыль, тыс.руб | ||||
октябрь 2006 г. |
ноябрь 2006 г. |
октябрь 2006 г. |
ноябрь 2006 г. |
Октябрь 2006 г. |
ноябрь 2006 г. |
октябрь 2006 г. |
ноябрь 2006 г. |
|
| А | 57 | 50 | 6.9 | 7.3 | 5.8 | 5.9 | 62.7 | 70 |
| Б | 69 | 61 | 8.1 | 8.2 | 6.9 | 7.2 | 82.8 | 61 |
| В | 80 | 66 | 7.2 | 7.5 | 5.6 | 6.1 | 128 | 92.4 |
| Г | 54 | 43 | 7 | 7.1 | 6.7 | 6.9 | 16.2 | 8.6 |
Для проведения факторного анализа выполним вспомогательные вычисления
| p1q1 | p0q1 | p1q0 | q1z1 | q1z0 | |
| А | 365 | 345 | 416.1 | 295 | 290 |
| Б | 500.2 | 494.1 | 565.8 | 439.2 | 420.9 |
| В | 495 | 475.2 | 600 | 402.6 | 369.6 |
| Г | 305.3 | 301 | 383.4 | 296.7 | 288.1 |
| Сумма | 1665.5 | 1615.3 | 1965.3 | 1433.5 | 1368.6 |
Рассчитаем индивидуальные индексы объема, цены, себестоимости и прибыли:
| Объем | Цена | Себестоимость | Прибыль | |
| А | 0.877193 | 1.057971 | 1.017241 | 1.116427 |
| Б | 0.884058 | 1.012346 | 1.043478 | 0.736715 |
| В | 0.825 | 1.041667 | 1.089286 | 0.721875 |
| Г | 0.796296 | 1.014286 | 1.029851 | 0.530864 |
Продукт А: прибыль выросла на 11,6% за счет роста цены на 5,8%. Рост прибыли снизило повышение себестоимости на 1,7% и снижение объема производства на 12,3%.
Продукт Б: несмотря на рост цены на 1,2% прибыль упала на 26,4% за счет повышения себестоимости на 4,3% и снижение объема производства на 11,6%.
Продукт А: несмотря на рост цены на 4,1% прибыль упала на 27,9% за счет повышения себестоимости на 8,9% и снижение объема производства на 17,5%.
Продукт А: несмотря на рост цены на 1,4% прибыль упала на 47% за счет повышения себестоимости на 2,99% и снижение объема производства на 20,4%.
Суммарно по продуктам имеем:
Цена выросла на 3,11%, объем снизился на 15,25%, себестоимость выросла на 4,74% , вследствие чего Индекс прибыли снизился на 20%.
Задание №34
По данным табл. 29 определить: 1) индивидуальные индексы себестоимости продукции; 2) общий индекс себестоимости; 3) провести анализ изменений затрат на рубль товарной продукции.
Таблица 29
| Продукция | Объём производства за месяц, т | Отпускная цена предприятия, тыс. руб. / т | Себестоимость 1 т продукции, тыс. руб. / т | |||
| июль 2005 г. | август 2005 г. | июль 2005 г. | август 2005 г. | Июль 2005 г. | Август 2005 г. | |
| А | 145 | 158 | 22 | 21,8 | 20 | 19,9 |
| Б | 208 | 266 | 15 | 14,1 | 13,5 | 12,8 |
| В | 176 | 183 | 20 | 19 | 17,2 | 16,6 |
| Г | 121 | 120 | 17 | 17,3 | 15,6 | 15,6 |
Решение:
Индивидуальный индекс себестоимости
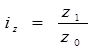
Индекс фактического изменения себестоимости сравнимой товарной продукции (сводный (общий) индекс себестоимости):
![]()
Последний показатель характеризует динамику себестоимости продукции. Поскольку в знаменателе индекса фигурирует фактическая себестоимость единицы продукции предыдущего года, то он охватывает только продукцию, сравнимую с предыдущим годом.
| Продукция | Объём производства за месяц, т | Себестоимость 1 т продукции, тыс. руб. / т | Индивидуальный индекс себестоимости | ||
| июль 2005 г. | Июль 2005 г. | Август 2005 г. | август 2005 г. | ||
| А | 145 | 20 | 19,9 | 158 | 0,995 |
| Б | 208 | 13,5 | 12,8 | 266 | 0,948148 |
| В | 176 | 17,2 | 16,6 | 183 | 0,965116 |
| Г | 121 | 15,6 | 15,6 | 120 | 1 |
Для расчета сводного индекса себестоимости проведем дополнительные расчеты:
| q1 z1 | q1 z0 | |
| А | 3144,2 | 2885,5 |
| Б | 3404,8 | 2662,4 |
| В | 3037,8 | 2921,6 |
| Г | 1872 | 1887,6 |
| Сумма | 11458,8 | 10357,1 |
Следовательно, общий индекс себестоимости равен 110,64%. Затраты на один рубль товарной продукции определяются отношением общей суммы затрат на производство и реализацию продукции к товарному выпуску продукции, исчисленной в оптовых ценах:
З1ртп = qc/qz
где: З1ртп – затраты на один рубль товарной продукции;
q – количество, объем выпуска в натуральном выражении;
с – себестоимость;
z – цена.
| qc0 | qc1 | qz0 | qz1 | З1ртп0 | З1ртп0 |
| 3190,00 | 3444,40 | 2900,00 | 3144,20 | 0,91 | 0,91 |
| 3120,00 | 3750,60 | 2808,00 | 3404,80 | 0,90 | 0,91 |
| 3520,00 | 3477,00 | 3027,20 | 3037,80 | 0,86 | 0,87 |
| 2057,00 | 2076,00 | 1887,60 | 1872,00 | 0,92 | 0,90 |
Изменение уровня себестоимости отдельных изделий зависит от:
– изменения цен на сырье, материалы, топливо и т.д., тарифов на энергию, грузовые перевозки;
– изменения затрат по отдельным статьям себестоимости.
Снижение оптовых цен при прочих равных условиях увеличивает затраты на один рубль товарной продукции, и наоборот.
Для того чтобы определить фактическую экономию (перерасход) на весь выпуск, необходимо экономию (перерасход) на один рубль товарной продукции умножить на фактический выпуск товарной продукции.
Для того чтобы определить влияние факторов на изменение суммы прибыли, необходимо абсолютные приросты (снижения) затрат на один рубль товарной продукции за счет каждoгo фактора умножить на фактический объем реализации, выраженный в плановых ценах.
Задание №40
По данным табл. 35 проанализировать динамику и причины изменений средней себестоимости 1 т продукции, производимой разными предприятиями отрасли в регионе.
Таблица 35
| Завод-изготовитель | Объём производства продукции, т | Себестоимость 1т продукции, тыс. руб. / т | ||
| март 2005 г. | март 2006 г. | март 2005 г. | март 2006 г. | |
| МЗ № 1 | 250 | 210 | 22 | 24,5 |
| МЗ № 2 | 430 | 370 | 23 | 23,9 |
| МЗ № 3 | 320 | 290 | 23,5 | 24, 2 |
| МЗ № 4 | 240 | 250 | 22,5 | 23,7 |
Решение:
Индивидуальный индекс себестоимости:
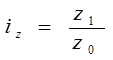
Индекс фактического изменения себестоимости сравнимой товарной продукции (сводный (общий) индекс себестоимости):
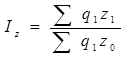
Общее изменение себестоимости единицы продукции:
![]()
в том числе за счёт изменения:
а) объёма производства продукции ![]() ;
;
б) суммы постоянных затрат ![]() ;
;
в) суммы удельных переменных затрат ![]() .
.
| Индивидуальный индекс объема | Индивидуальный индекс себестоимости | q0z0 | q1z1 | q1z0 | Индекс фактического изменения себестоимости |
| 0,84 | 1,113636 | 5500 | 5145 | 4620 | 1,113636 |
| 0,860465 | 1,03913 | 9890 | 8843 | 8510 | 1,03913 |
| 0,90625 | 1,029787 | 7520 | 7018 | 6815 | 1,029787 |
| 1,041667 | 1,053333 | 5400 | 5925 | 5625 | 1,053333 |
Сводный (общий) индекс себестоимости по четырем предприятиям составляет 1,053226.
Исходя из полученных результатов, можно сделать следующие выводы: анализ изменений затрат на рубль товарной продукции показывает, что объем производства по всем предприятиям отрасли кроме четвертого снизился, это отображается индивидуальными индексами объема производства продукции. Прямые трудовые затраты наряду с материальными являются важнейшей статьей себестоимости продукции. Они оказывают большое влияние на формирование ее уровня. В себестоимости продукции (работ, услуг) расходы на обслуживание и управление занимают значительный удельный вес. Эти расходы называются комплексными, так как они состоят из нескольких экономических элементов
Себестоимость 1 т продукции по всем предприятиям отрасли возросла что вызвано изменением всех выше перечисленных факторов.