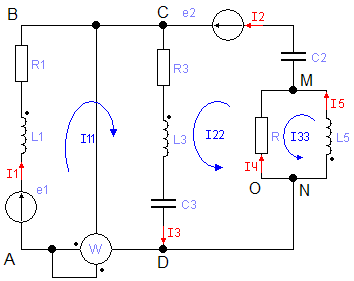
Расчет разветвленной цепи синусоидального тока
СОДЕРЖАНИЕ: Федеральное агентство образования ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Курсовая работа «Расчет разветвленной цепиФедеральное агентство образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ
(ТУСУР)
Курсовая работа
«Расчет разветвленной цепи
синусоидального тока»
По дисциплине
«Общая электротехника и электроника»
Авторы учебно-методического пособия:
В.М. Дмитриев, Н.В. Кобрина, Н.П. Фикс, В.И. Хатников
Томск 2000
Вариант №15
Выполнил студент группы
«» 2008 г.
2008
Задание на курсовую работу .
Расчет разветвленной цепи синусоидального тока.
1. Cчитая, что индуктивная связь между катушками отсутствует:
1.1 составить систему уравнений в символической форме по методу контурных токов;
1.2 преобразовать схему до двух контуров;
1.3 в преобразованной схеме рассчитать токи по методу узловых потенциалов;
1.4 рассчитать ток в третьей ветви схемы (в ветви, обозначения компонентов которой имеют индекс 3) методом эквивалентного генератора и записать его мгновенное значение;
1.5 на одной координатной плоскости построить графики ![]() и
и ![]() или
или ![]() ;
;
1.6 рассчитать показание ваттметра;
1.7 составить баланс активных и реактивных мощностей;
1.8 определить погрешность расчета;
1.9 построить лучевую диаграмму токов и топографическую диаграмму напряжений для преобразованной схемы.
2. С учетом взаимной индуктивности для исходной схемы составить систему уравнений по законам Кирхгофа для мгновенных значений и в комплексной форме.
3. Выполнить развязку индуктивной связи и привести эквивалентную схему замещения.
Указания
. Сопротивление R
в расчетных схемах принять равным 10 Ом. При расчете принять, что ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Начальную фазу ЭДС
. Начальную фазу ЭДС ![]() принять равной нулю, а начальные фазы ЭДС
принять равной нулю, а начальные фазы ЭДС ![]() и
и ![]() — значениям
— значениям ![]() из таблицы.
из таблицы.
| 25 | 50 | 75 | 30 | 15 | 20 | 25 | 15 | 20 | 10 |
| 200 | 0,1 | 0,1 | 0,1 | 200 | 400 | 200 |
1. Считая, что индуктивная связь между катушками отсутствует:
1.1 Составим систему уравнений в символической форме по методу контурных токов.
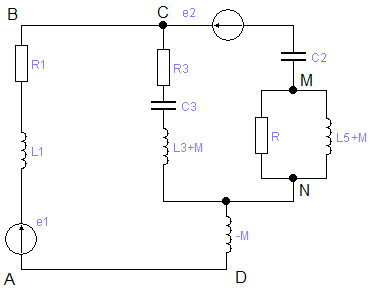
Предварительно произвольно выберем направление токов в ветвях и направления контурных токов, с которыми совпадает направление обхода контуров. Таким образом по второму закону Кирхгофа имеем систему из трех уравнений:
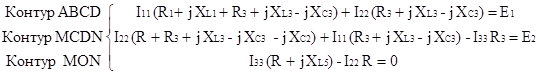
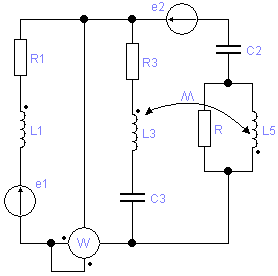
1.2 Преобразуем схему до двух контуров.
Заменим две параллельных ветви R и jXL 5 одной эквивалентной с сопротивлением R и jXL соединенных последовательно. Где Z MN – полное сопротивление этого участка.
Z
MN
= ![]() = R + jXL
= R + jXL
Таким образом мы получим два контура.
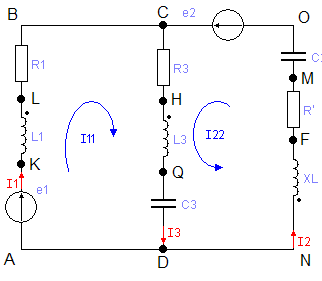
И по второму закону Кирхгофа составим два уравнения:
![]()
1.3 В преобразованной схеме рассчитаем токи по методу узловых потенциалов.
Примем D = 0, тогда мгновенные значения э.д.с имеют вид:
![]() ;
; ![]() ;
;
где ![]() ;
; ![]() .
.
Затем определим модули реактивных сопротивлений элементов цепи:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Определим эквивалентное сопротивление участка MN:
Z
MN
= 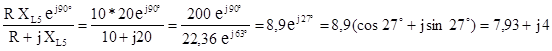
Т.е. R = 7,93 Ом; XL = 4 Ом.
Так как цепь имеет два узла, то остается одно уравнение по методу двух узлов:
![]() , где g1
, g2
, g3
– проводимости ветвей.
, где g1
, g2
, g3
– проводимости ветвей.
Рассчитаем проводимости каждой из ветвей:
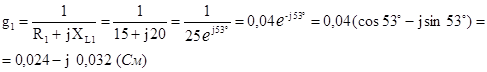

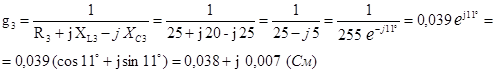
Считаем E
1
= E1
= 25 (В)
;![]()
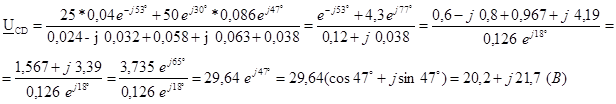
Определим токи в каждой из ветвей:
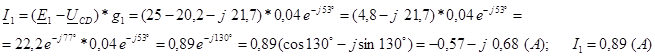
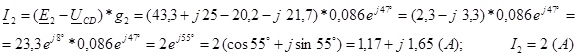
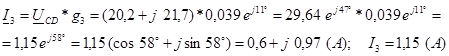
Произведем проверку, применив первый закон Кирхгофа для узла C:
I 3 = I 1 + I 2 = – 0,57 – j 0,68 +1,17 + j 1,65 = 0,6 + j 0,97
Токи совпадают, следовательно, расчет произведен верно.
1.4 Рассчитаем ток в третьей ветви схемы методом эквивалентного генератора.
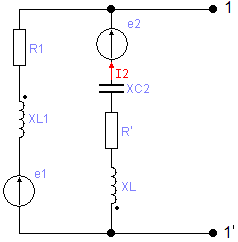
Определим напряжение холостого хода относительно зажимов 1-1’
![]()
где ![]()
![]()
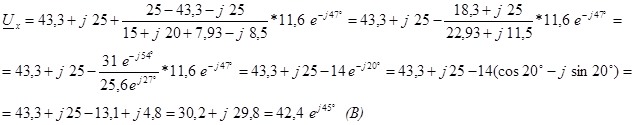
Сначала определим внутреннее входное сопротивление:
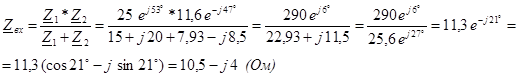
Затем определим ток в третьей ветви:
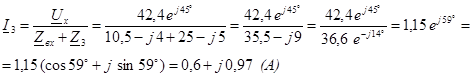
Значение тока I3 совпадает со значением тока при расчете методом узловых потенциалов, что еще раз доказывает верность расчетов.
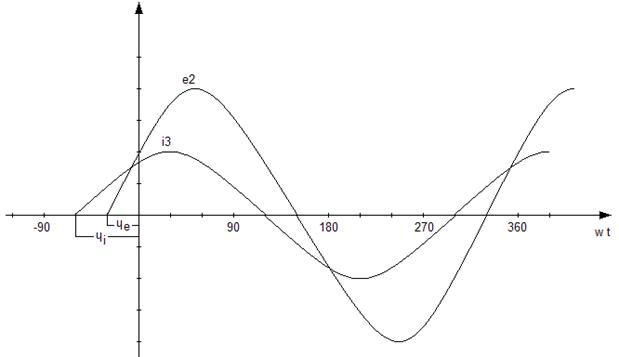
1.5 На одной координатной плоскости построим графики i 3 ( t ) и e 2 ( t ).
![]() ;
; ![]()
где ![]() ;
; ![]() (А)
(А)
Тогда: ![]() ;
; ![]()
Начальная фаза для ![]() :
: ![]() , для
, для ![]() :
: ![]()
Выберем масштаб me = 17,625 (В/см) ; mi = 0,8 (А/см).
То есть два деления для тока 1,6 А, четыре деления для Э.Д.С. 70,5 В.
1.6 Определим показания ваттметра.
![]()
1.7 Составим баланс активных и реактивных мощностей.
Должно выполняться условие:
![]()
![]()
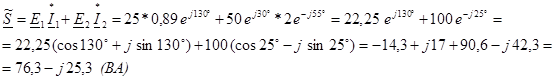
где P = 76,3 (Вт); Q = - 25,3 (вар) (Характер нагрузки активно-емкостный)
Или ![]()
Первый источник работает в режиме потребителя, второй в режиме генератора.
![]()
1.8 Определим погрешности расчета мощности:
![]() - для активной мощности
- для активной мощности
![]() - для реактивной мощности
- для реактивной мощности
Погрешности связаны с округлениями при расчете, они находятся в допустимых пределах.
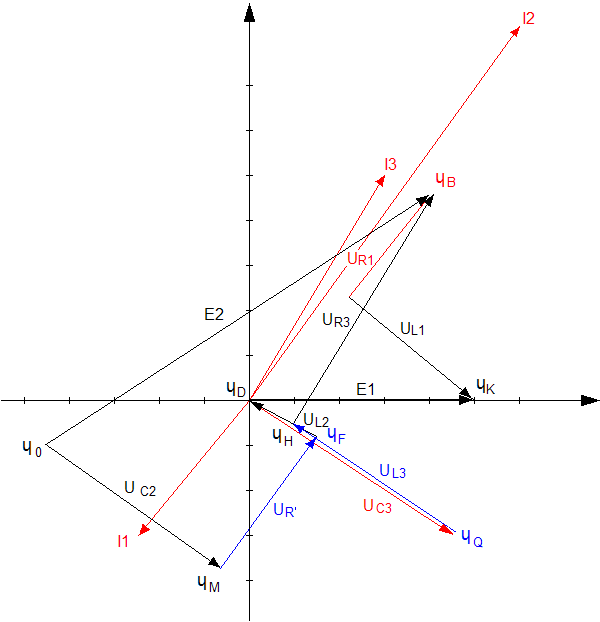
1.9 Построим лучевую диаграмму токов и топографическую диаграмму напряжений для преобразованной цепи.
Определим потенциалы точек.
Пусть ![]() , т.е.
, т.е. ![]() .
.
Тогда ![]() (В)
(В)
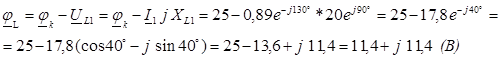

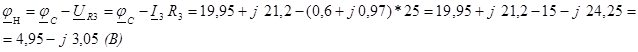
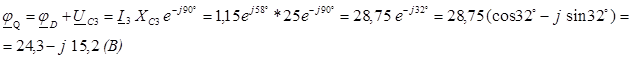
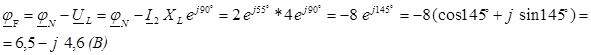
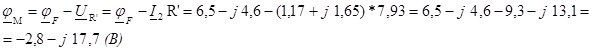
![]()
Выберем масштаб: ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]()
2. С учетом взаимной индуктивности для исходной схемы составим систему уравнений Кирхгофа для мгновенных значений и в комплексной форме.
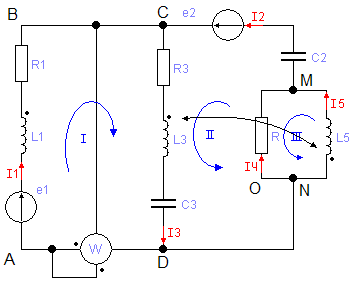
Из схемы следует, что обмотки L3 и L5 соединены встречно и связаны взаимной индуктивностью, тогда:
Для контура ABCD:
![]()
Для контура CDNOM:
![]()
Для контура MON:
![]()
Для узла С:
![]()
Для узла M:
![]()
Потенциалы точек A, D, N одинаковы.
3. Выполним развязку индуктивной связи и приведем эквивалентную схему замещения.
Ветви соединены параллельно, таким образом напряжение на всех ветвях одинаково.
![]() - взаимная индуктивность катушек, где K
св
- коэффициент связи, не превышающий 1.
- взаимная индуктивность катушек, где K
св
- коэффициент связи, не превышающий 1.
Список использованной литературы:
1. В.М. Дмитриев, Н.В. Кобрина, Н.П. Фикс, В.И. Хатников.
Теоретические основы электротехники. Ч.1: Установившиеся режимы в линейных электрических цепях: Учебное методическое пособие. - Томск: Томский межвузовский центр дистанционного образования, 2001. - 51 с.
2. В.М. Дмитриев, Н.В. Кобрина, Н.П. Фикс, В.И. Хатников.
Теоретические основы электротехники. Ч. 1: Установившиеся режимы в линейных электрических цепях.— Томск: Томский межвузовский центр дистанционного образования, 2001.— 157 с.