Задание на курсовую работу > Общая постановка задачи Содержание пояснительной записки
СОДЕРЖАНИЕ: В будущем, в связи с усложнением науки, техники, экономики значение правильного управления ими будет расти, и поэтому будет возрастать и значение информацииСОДЕРЖАНИЕ
Введение……………………………………………………………………4
1. Задание на курсовую работу……………………………………………5
1.1. Общая постановка задачи………………………………………….….5
1.2. Содержание пояснительной записки …………………………….… 8
1.3. Правила оформления пояснительной записки……………………....8
2. Некоторые теоретические сведения и методические указания
к выполнению курсовой работы…………………………………….…..9
2.1. Системы и каналы связи………………… ……………………………9
2.2. Модель источника сообщений……………………………………….10
2.3. Энтропия источника сообщений…………………………………….11
2.4. Кодер источника ……………….…………………………………….12
2.4.1. Код Шеннона – Фанно…………..…………………………………12
2.4.2. Код Хаффмана…….………………………………………………..14
2.5. Замечания относительно алфавита и характеристик
обобщенного источника сообщений…………………………………17
2.6. Дискретные каналы связи…………….………………………………18
2.7. Оптимальное решающее правило восстановления символа
при приеме по критерию минимума вероятности средней
ошибки…………………………………………………………………19
Введение В современной науке, технике и общественной жизни большую роль играет информация и связанные с ней операции: получение, передача, преобразование, хранение и т.д. Значение информации в современном обществе, по-видимому, переросло значение другого важного фактора, игравшего ранее доминирующую роль, а именно – энергии. В будущем, в связи с усложнением науки, техники, экономики значение правильного управления ими будет расти, и поэтому будет возрастать и значение информации.Теория информации как дисциплина, представляет собой одну из ветвей статистической теории связи. Круг ее проблем, составляющих содержание т.н. «шеноновской теории информации» можно трактовать как исследование методов кодирования, преобразования информации для рационального представления сообщений различных источников и для надежной передачи сообщений по зашумленным каналам связи. В любом реальном канале связи помимо полезного сигнала неизбежно присутствуют помехи, возникающие по многим причинам, - из-за хаотического теплового движения электронов в элементах цепей, несовершенства контактов в аппаратуре, влияния соседних радиоканалов с близкими несущими частотами, наличия в пространстве шумового космического радиоизлучения и т.д. Это значит, что любой реальный канал зашумлен. Способность радиотехнических средств передачи информации противодействовать вредному влиянию помех и обеспечивать высокую достоверность передачи называют помехоустойчивостью. В современной радиотехнике задача создания помехоустойчивых систем является одной из центральных. Предельные возможности различных методов обработки и передачи сообщений зависит от статистических свойств источников и каналов. В предлагаемой курсовой работе рассматривается математическая модель канала связи, ряд характеристик которой следует рассчитать. На первом расчетном этапе выполнения работы необходимо исследовать статистические характеристики модели источника сообщений.На втором этапе – закодировать передаваемые сообщения. В связи с тем, что алгебраическая теория кодирования будет изучаться вами в рамках дисциплины «Теория кодирования», выбор методов преобразования информации, предлагаемых в данной курсовой работе, ограничен. Это коды Шеннона-Фано и Хаффмана.Третий этап работы связан и исследованием свойств зашумленного канала передачи информации.Перед началом выполнения задания рекомендуется просмотреть теоретический материал. В качестве учебной литературы для этой цели рекомендуется книга В.Д. Колесника и Г.Ш. Полтырева «Курс теории информации»
1
. ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
![]()
1.1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ
Задана некоторая система связи для передачи дискретных сообщений.
Характеристики источника сообщений представлены в табл. 1. Для передачи сообщения по каналу связи, в зависимости от варианта работы, используется либо код Хаффмена, либо код Шеннона – Фано. Канал связи зашумлен, т.е. принимаемый символ не обязательно совпадает с переданным. В предположении стационарности и отсутствия памяти у канала его переходные вероятности имеют числовые значения, представленные в табл. 2 и 3 (для сильно и слабо зашумленных каналов соответственно).
В процессе выполнения работы необходимо проделать следующее.
1. Составить обобщенную структурную схему системы связи для передачи дискретных сообщений, содержащую источник сообщений, кодер, модулятор, канал связи, демодулятор, декодер и приемник сообщений. Изобразить качественные временные диаграммы сигналов во всех промежуточных точках структурной схемы. Вид модуляции выбирается студентом самостоятельно. Все диаграммы должны сопровождаться словесными описаниями.
2. Определить количество информации, содержащейся в каждом элементарном сообщении источника, энтропию и избыточность источника информации.
3. Построить код Шеннона-Фано или Хаффмана (в зависимости от задания варианта) для сообщений источника.
4. Рассчитать вероятности появления двоичных символов, передаваемых по каналу. Определить скорость передачи информации по каналу в предположении отсутствия помех. Вычислить пропускную способность канала, сравнить ее величину со скоростью передачи информации.
5. Определить оптимальное по минимуму вероятности средней ошибки правило восстановления символа при приеме в условиях сильно зашумленного канала.
6. Вычислить среднюю вероятность ошибки при передаче сообщения по слабо зашумленному каналу.
7. Оценить вероятность правильного приема последовательности сообщений, заданной в табл. 3.
Таблица 1
Алфавит источника и вероятности символов
| № |
а |
б |
в |
г |
д |
ж |
з |
и |
к |
л |
м |
н |
о |
п |
| 1 |
0,069 |
0,019 |
0,052 |
0,007 |
0,09 |
0,06 |
0,101 |
0,11 |
0,062 |
0,053 |
0.1 |
0,09 |
0,115 |
0,072 |
| 2 |
0.035 |
0.11 |
0.049 |
0,089 |
0.001 |
0.036 |
0.077 |
0.11 |
0.064 |
0.097 |
0.06 |
0.098 |
0.078 |
0.096 |
| 3 |
0.091 |
0.024 |
0.067 |
0.082 |
0.119 |
0.027 |
0.078 |
0.111 |
0.023 |
0.022 |
0.11 |
0.068 |
0.153 |
0.025 |
| 4 |
0.105 |
0.025 |
0.105 |
0.02 |
0.094 |
0.036 |
0.086 |
0.093 |
0.016 |
0.107 |
0.066 |
0.055 |
0.122 |
0.07 |
| 5 |
0.055 |
0.1 |
0.054 |
0.116 |
0.087 |
0.023 |
0.099 |
0.059 |
0.003 |
0.067 |
0.062 |
0.099 |
0.077 |
0.099 |
| 6 |
0.02 |
0.057 |
0.052 |
0.025 |
0.151 |
0.109 |
0.047 |
0.05 |
0.146 |
0.038 |
0.05 |
0.021 |
0.136 |
0.098 |
| 7 |
0.064 |
0.102 |
0.034 |
0.085 |
0.092 |
0.074 |
0.102 |
0.028 |
0.026 |
0.067 |
0.014 |
0.014 |
0.167 |
0.131 |
| 8 |
0.032 |
0.058 |
0.089 |
0.064 |
0.086 |
0.122 |
0.089 |
0.081 |
0.026 |
0.079 |
0.035 |
0.086 |
0.083 |
0.07 |
| 9 |
0.099 |
0.083 |
0.107 |
0.077 |
0.121 |
0.097 |
0.089 |
0.042 |
0.041 |
0. 014 |
0.113 |
0.021 |
0.011 |
0.085 |
| 10 |
0.082 |
0.061 |
0.07 |
0.023 |
0.111 |
0.124 |
0.131 |
0.045 |
0.019 |
0.118 |
0.091 |
0.011 |
0.098 |
0.016 |
| 11 |
0.074 |
0.102 |
0.034 |
0.095 |
0.092 |
0.084 |
0.102 |
0.018 |
0.026 |
0.057 |
0.04 |
0.014 |
0.167 |
0.131 |
| 12 |
0.065 |
0.1 |
0.064 |
0.116 |
0.097 |
0.023 |
0.089 |
0.059 |
0.003 |
0.057 |
0.052 |
0.099 |
0.077 |
0.089 |
| 13 |
0.097 |
0.008 |
0.007 |
0.111 |
0.064 |
0.036 |
0.116 |
0.018 |
0.01 |
0.016 |
0.1 |
0.16 |
0.128 |
0.039 |
| 14 |
0.14 |
0.083 |
0.021 |
0.051 |
0.014 |
0.092 |
0.137 |
0.084 |
0.056 |
0.101 |
0.038 |
0.047 |
0.102 |
0.034 |
| 15 |
0.107 |
0.084 |
0.094 |
0.104 |
0.063 |
0.087 |
0.009 |
0.081 |
0.022 |
0.071 |
0.053 |
0.106 |
0.035 |
0.084 |
| 16 |
0.02 |
0.067 |
0.052 |
0.035 |
0.141 |
0.109 |
0.037 |
0.05 |
0.136 |
0.038 |
0.05 |
0.021 |
0.126 |
0.098 |
| 17 |
0,059 |
0,019 |
0,062 |
0,017 |
0,08 |
0,06 |
0,104 |
0,11 |
0,062 |
0,05 |
0.11 |
0,08 |
0,115 |
0,072 |
| 18 |
0.099 |
0.093 |
0.107 |
0.087 |
0.131 |
0.097 |
0.079 |
0.042 |
0.031 |
0.014 |
0.113 |
0.021 |
0.011 |
0.075 |
| 19 |
0.105 |
0.035 |
0.105 |
0.02 |
0.094 |
0.046 |
0.096 |
0.083 |
0.016 |
0.107 |
0.056 |
0.045 |
0.122 |
0.07 |
| 20 |
0.101 |
0.011 |
0.074 |
0.059 |
0.079 |
0.088 |
0.035 |
0.099 |
0.08 |
0.073 |
0.09 |
0.096 |
0.106 |
0.009 |
| 21 |
0.045 |
0.11 |
0.059 |
0.099 |
0.001 |
0.046 |
0.067 |
0.11 |
0.054 |
0.097 |
0.06 |
0.088 |
0.078 |
0.086 |
| 22 |
0.082 |
0.071 |
0.07 |
0.033 |
0.111 |
0.134 |
0.131 |
0.035 |
0.019 |
0.1 18 |
0.081 |
0.011 |
0.088 |
0.016 |
| 23 |
0.042 |
0.058 |
0.099 |
0.064 |
0.096 |
0.122 |
0.079 |
0.081 |
0.016 |
0.079 |
0.025 |
0.086 |
0.073 |
0.07 |
| 24 |
0.091 |
0.034 |
0.067 |
0.092 |
0.119 |
0.037 |
0. 068 |
0.111 |
0.013 |
0.022 |
0.11 |
0.058 |
0.153 |
0.025 |
| 25 |
0,039 |
0,01 |
0,052 |
0,007 |
0,09 |
0,06 |
0,132 |
0,119 |
0,042 |
0,073 |
0.1 |
0,09 |
0,115 |
0,071 |
Таблица 2
Способ кодирования и элементы матрицы перехода
в сильно зашумленном канале
| № вар. |
Вид кода |
|
|
№ вар. |
Вид кода |
|
|
| 1 |
Х |
0.38 |
0.62 |
13 |
Ш-Ф |
0.79 |
0.27 |
| 2 |
Х |
0.29 |
0.71 |
14 |
Ш-Ф |
0.75 |
0.32 |
| 3 |
Ш-Ф |
0.36 |
0.59 |
15 |
Х |
0.69 |
0.31 |
| 4 |
Х |
0.28 |
0.69 |
16 |
Х |
0.75 |
0.28 |
| 5 |
Х |
0.31 |
0.59 |
17 |
Х |
0.71 |
0.35 |
| 6 |
Ш-Ф |
0.36 |
0.61 |
18 |
Ш-Ф |
0.58 |
0.41 |
| 7 |
Х |
0.32 |
0.67 |
19 |
Х |
0.69 |
0.33 |
| 8 |
Ш-Ф |
0.24 |
0.70 |
20 |
Ш-Ф |
0.61 |
0.35 |
| 9 |
Ш-Ф |
0.27 |
0.69 |
21 |
Х |
0.59 |
0.39 |
| 10 |
Х |
0.32 |
0.77 |
22 |
Х |
0.67 |
0.4 |
| 11 |
Х |
0.21 |
0.70 |
23 |
Ш-Ф |
0.71 |
0.31 |
| 12 |
Ш-Ф |
0.35 |
0.68 |
24 |
Х |
0.62 |
0.28 |
| 25 |
Х |
0.61 |
0.34 |
||||
Здесь введены обозначения:
Х - код Хаффмена, Ш- Ф - код Шеннона-Фано
Таблица 3
Вероятности переходов и вид последовательности сообщений для слабо зашумленного канала связи
| № вар. |
|
|
Послед. сообщен. |
№ вар. |
|
|
Послед. сообщен. |
| 1 |
0.957 |
0.039 |
кира |
13 |
0.035 |
0.977 |
жора |
| 2 |
0.921 |
0.065 |
пила |
14 |
0.021 |
0.943 |
бомж |
| 3 |
0.965 |
0.047 |
клаб |
15 |
0.027 |
0.978 |
дома |
| 4 |
0.938 |
0.056 |
жбан |
16 |
0.065 |
0.925 |
зима |
| 5 |
0.976 |
0.045 |
рома |
17 |
0.034 |
0.973 |
лика |
| 6 |
0.959 |
0.076 |
гонг |
18 |
0.051 |
0.945 |
дока |
| 7 |
0.969 |
0.062 |
бора |
19 |
0.062 |
0.955 |
нора |
| 8 |
0.981 |
0.075 |
азик |
20 |
0.041 |
0.928 |
жлоб |
| 9 |
0.957 |
0.049 |
гном |
21 |
0.039 |
0.947 |
кило |
| 10 |
0.968 |
0.078 |
липа |
22 |
0.057 |
0.967 |
рама |
| 11 |
0.976 |
0.081 |
вода |
23 |
0.048 |
0.954 |
клон |
| 12 |
0 0.965 |
0.054 |
жало |
24 |
0.032 |
0.959 |
вагон |
| 25 |
0.078 |
0.969 |
банк |
||||
1.2. Содержание пояснительной записки
Структура пояснительной записки к курсовой работе и последовательность изложения результатов выполнения должны быть следующими.
1. Титульный лист.
2. Оглавление (Содержание).
3. Введение.
4. Задание и исходные данные в соответствии с номером варианта.
5. Обобщенная структурная схема системы связи для передачи дискретных сообщений.
6. Расчет информационных характеристик источника.
7. Построение кода для сообщений источника.
8. Статистические характеристики закодированных сообщений.
9. Оптимальное по минимуму средней ошибки правило восстановления символа при приеме в условиях сильно зашумленного канала.
10. Ошибки в передаче сообщений по слабо зашумленному каналу.
11. Заключение.
12. Список использованной литературы.
1.3. Правила оформления пояснительной записки
1. В пояснительной записке все пункты выполнения курсовой работы должны располагаться в той последовательности, которая приведена выше, иметь ту же нумерацию и те же заголовки. В зависимости от сложности выполняемого задания разрешается вводить подпункты, структурирующие изложение материала. В начале каждого пункта кратко излагаются необходимые элементы теории.
2. Основные полученные аналитические формулы должны иллюстрироваться рисунками, дающими представление о качественном характере поведения исследуемых величин и процессов. Рисунки должны быть пронумерованы и иметь подписи.
3. В пояснительной записке должны быть введение и заключение. Во введении формулируются цели курсовой работы с учётом её содержания. В заключении даётся краткий анализ результатов с отражением их особенностей.
4. Оглавление курсовой работы располагается после титульного листа, именуется как Содержание и состоит из номеров и названий разделов с указанием номеров страниц.
5. Курсовая работа оформляется на стандартных листах формата А4. Шрифт для основного текста Times New Roman Cyr, размер 14 пунктов. Текстовая часть проекта выполняется по ГОСТ 2.105-95 Общие требования к текстовым документам. Листы должны быть надежно скреплены, страницы пронумерованы.
6. Список использованной литературы оформляется в соответствии с ГОСТ 7.32-91 и приводится на последней странице работы.
7. Текст курсовой работы должен быть расположен на одной стороне листа. Обратная (чистая) сторона листа используется для пояснений и исправлений в соответствии с замечаниями преподавателя, если после рецензирования исправления и комментарии потребуются.
8. После внесения замечаний преподавателя замена листов не допускается. Можно лишь вклеивать дополнительные листы с исправлениями.
2. Некоторые теоретические сведения и методические указания к выполнению курсовой работы
2.1. СИСТЕМЫ и каналы связи
Системой связи называют совокупность технических средств, необходимых для передачи сообщения от источника к получателю ![]() . Обычно в изображение общей функциональной схемы системы связи включают и источник, и получатель сообщения. Каналом связи называется совокупность устройств и линий связи, которые сигнал проходит последовательно между любыми двумя точками системы связи. Понятие канала является, таким образом, очень широким: канал в простейшем случае может состоять из пары проводов, в то же время при передаче сообщения с одного континента на другой канал включает многочисленные формирующие, коммутирующие, преобразующие, усиливающие, фильтрующие устройства и различные среды распространения колебаний (волноводы, кабели, свободное пространство, кварцевое стекло оптоволоконных линий и т.д.).
. Обычно в изображение общей функциональной схемы системы связи включают и источник, и получатель сообщения. Каналом связи называется совокупность устройств и линий связи, которые сигнал проходит последовательно между любыми двумя точками системы связи. Понятие канала является, таким образом, очень широким: канал в простейшем случае может состоять из пары проводов, в то же время при передаче сообщения с одного континента на другой канал включает многочисленные формирующие, коммутирующие, преобразующие, усиливающие, фильтрующие устройства и различные среды распространения колебаний (волноводы, кабели, свободное пространство, кварцевое стекло оптоволоконных линий и т.д.).
В работе рассматривается простейшая модель канала связи, состоящая из модулятора, передатчика, линии связи (среды распространения сигнала), приемника и демодулятора. Кодер и декодер канала в данной работе не рассматриваются, т.к. соответствующий материал отнесен к следующему курсу – «Теория кодирования». Он опирается на другой математический аппарат и известен как алгебраическая теория кодирования. Рассматриваемый в работе метод кодирования может интерпретироваться как результат функционирования кодера источника сообщений и включаться в обобщенную модель источника. Аналогичное справедливо и для декодера, с той лишь разницей, что он вносится в обобщенную модель получателя сообщений.
Таким образом, предлагаемая модель системы связи состоит из обобщенных моделей источника и получателя сообщений и модели канала связи.
2.2. МОДЕЛЬ ИСТОЧНИКА СООБЩЕНИЙ
С точки зрения получателя сообщений источник можно рассматривать как некоторый эксперимент с известным набором возможных исходов. В каждом таком эксперименте возможен только один исход, но какой именно – неизвестно. Можно лишь указать вероятность того или иного исхода. Говорят, что источник сообщений задан, если известен набор исходов ![]() и заданы вероятности этих исходов
и заданы вероятности этих исходов ![]() . Другими словами источник задан, если задано множество упорядоченных пар
. Другими словами источник задан, если задано множество упорядоченных пар ![]() . Если множество исходов конечно (иногда можно расширять это ограничение до счетности множества), то источник называется дискретным. Заметим, что и канал передачи информации в этом случае называется дискретным.
. Если множество исходов конечно (иногда можно расширять это ограничение до счетности множества), то источник называется дискретным. Заметим, что и канал передачи информации в этом случае называется дискретным.
Полагается, что в единицу времени ![]() выдает одно сообщение. Источник называется источником без памяти, если каждый раз сообщение выдается абсолютно случайно, без учета того, какое сообщение было воспроизведено до этого. Это серьезное ограничение, существенно упрощающее решение проблем, возникающих при передаче информации.
выдает одно сообщение. Источник называется источником без памяти, если каждый раз сообщение выдается абсолютно случайно, без учета того, какое сообщение было воспроизведено до этого. Это серьезное ограничение, существенно упрощающее решение проблем, возникающих при передаче информации.
Источник обычно «генерирует» последовательно не одно, а несколько сообщений. Такую последовательность сообщений можно представить как случайный процесс с дискретным пространством состояний. На рис. 1 представлена одна из реализаций такого случайного процесса.
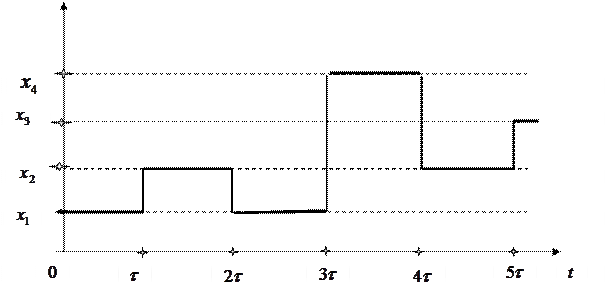
Рис. 1. Одна из реализаций случайного процесса, иллюстрирующая процесс «генерации» источником последовательности сообщений
Для закрепления этого материала постройте еще пару отличных от приведенной на рис.1 реализации случайного процесса. При мощности множества ![]() равной
равной ![]() на временном интервале
на временном интервале ![]() можно построить
можно построить ![]() различных процессов. В частности, для случая, изображенного на рис. 1, число таких процессов (различных последовательностей сообщений) будет равно
различных процессов. В частности, для случая, изображенного на рис. 1, число таких процессов (различных последовательностей сообщений) будет равно ![]() .
.
2.3. ЭНТРОПИЯ ИСТОЧНИКА СООБЩЕНИЙ
Получатель знает весь набор возможных сообщений, которые могут быть ему направлены, но какое именно сообщение передано ему сейчас – для него тайна. Именно в этом и заключается неопределенность состояния получателя. Если сообщение принято и есть уверенность, что понято правильно, то неопределенность исчезает. Другими словами сообщение содержало в себе ровно столько информации, сколько было неопределенности у получателя.
Таким образом, центральным вопросом становится способ определения меры неопределенности сообщения. Эта величина называется энтропией (точно также как в статистической термодинамике).
Если источник информации ![]() , располагающий алфавитом из
, располагающий алфавитом из ![]() букв, передал «случайно для себя» букву
букв, передал «случайно для себя» букву ![]() , то количество переданной информации составит, согласно Шеннону, величину
, то количество переданной информации составит, согласно Шеннону, величину ![]() . Чем больше вероятность
. Чем больше вероятность ![]() , тем меньшее количество информации было передано. Для лучшего понимания этого приведем пример. Хороший (успевающий) студент пошел сдавать экзамен. Априори известно, что с вероятностью
, тем меньшее количество информации было передано. Для лучшего понимания этого приведем пример. Хороший (успевающий) студент пошел сдавать экзамен. Априори известно, что с вероятностью ![]() он сдаст экзамен (по крайней мере, статистика предшествующих сессий давала основания так полагать), а с вероятностью
он сдаст экзамен (по крайней мере, статистика предшествующих сессий давала основания так полагать), а с вероятностью ![]() – «провалится». Какое количество информации мы получим, узнав о результате экзамена? Если экзамен сдан, то
– «провалится». Какое количество информации мы получим, узнав о результате экзамена? Если экзамен сдан, то ![]() бит. Мы получили маленькое количество информации, да это и понятно, мы и без того знали, что студент хороший. Но если он «провалил» экзамен, то это неожиданная новость. Она несет в себе много информации -
бит. Мы получили маленькое количество информации, да это и понятно, мы и без того знали, что студент хороший. Но если он «провалил» экзамен, то это неожиданная новость. Она несет в себе много информации - ![]() бита.
бита.
Таким образом, количество передаваемой информации зависит от того, какое именно сообщение передано, а это сообщение случайно! Поэтому
![]() (1)
(1)
носит название случайной энтропии. Обычно в теории информации работают со средними значениями, поэтому источник принято характеризовать средней (больцмановской) энтропией, определяемой по формуле:
![]() . (2)
. (2)
Здесь под символом ![]() понимается
понимается ![]() – все множество реализаций источника, т.е. его алфавит. Далее значок среднего будем опускать, понимая под энтропией именно среднюю энтропию, энтропию конкретного сообщения будем оговаривать отдельно.
– все множество реализаций источника, т.е. его алфавит. Далее значок среднего будем опускать, понимая под энтропией именно среднюю энтропию, энтропию конкретного сообщения будем оговаривать отдельно.
Можно показать, что средняя энтропия максимальна, если все сообщения равновероятны, т.е.
![]() и
и ![]() . (3)
. (3)
Алфавит может иметь вероятностное распределение, далекое от равномерного. Если некоторый исходный алфавит содержит ![]() символов, то его имеет смысл сравнить с «оптимизированным алфавитом», вероятностное распределение которого равномерно. Разность между максимально возможным значением энтропии сообщения –
символов, то его имеет смысл сравнить с «оптимизированным алфавитом», вероятностное распределение которого равномерно. Разность между максимально возможным значением энтропии сообщения – ![]() и средней энтропией рассматриваемого источника –
и средней энтропией рассматриваемого источника – ![]() принято называть избыточностью источника сообщений
принято называть избыточностью источника сообщений ![]() :
:
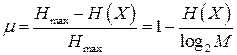 . (4)
. (4)
Избыточность показывает, насколько в среднем неплотно, при заданном алфавите, «упакована» информация в сообщениях источника. В частности избыточность современного английского текста составляет 50%, избыточность русского текста - 70%.
2.4. КОДЕР ИСТОЧНИКА
Для уменьшения избыточности источника ![]() используют энтропийное кодирование – кодирование словами (кодами) переменной длины, при которой длина кода символа имеет обратную зависимость от вероятности появления символа в передаваемом сообщении. Обычно энтропийные кодировщики используют для сжатия данных коды, длины которых пропорциональны отрицательному логарифму вероятности символа. Таким образом, наиболее вероятные символы используют наиболее короткие коды.
используют энтропийное кодирование – кодирование словами (кодами) переменной длины, при которой длина кода символа имеет обратную зависимость от вероятности появления символа в передаваемом сообщении. Обычно энтропийные кодировщики используют для сжатия данных коды, длины которых пропорциональны отрицательному логарифму вероятности символа. Таким образом, наиболее вероятные символы используют наиболее короткие коды.
2.4.1. КОД ШЕННОНА–ФАНО
Код Шеннона – Фано представляет собой метод сжатия информации схожий с алгоритмом Хаффмана, который появился несколькими годами позже. Алгоритм использует коды переменной длины: часто встречающийся символ кодируется кодом меньшей длины, редко встречающийся — кодом большей длины. Коды Шеннона — Фано префиксные, то есть никакое кодовое слово не является префиксом (группой первых символов) любого другого слова. Это свойство позволяет однозначно декодировать любую последовательность кодовых слов.
Основные этапы создания кода.
1. Символы первичного алфавита М1 выписывают в порядке убывания вероятностей.
2. Символы полученного алфавита делят на две части, суммарные вероятности символов которых максимально близки друг другу.
3. В префиксном коде для первой части алфавита присваивается двоичная цифра «0», второй части — «1».
4. Полученные части рекурсивно делятся и их частям назначаются соответствующие двоичные цифры в префиксном коде.
Код Шеннона — Фано строится с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.
При построении кода Шеннона — Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n + 1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона — Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона — Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона — Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.
Кодирование Шеннона — Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона — Фано, поэтому более эффективным считается сжатие методом Хаффмана.
Пример построения кодового дерева Шеннона - Фано
Исходные символы:
A (частота встречаемости 50),
B (частота встречаемости 39),
C (частота встречаемости 18),
D (частота встречаемости 49),
E (частота встречаемости 35),
F (частота встречаемости 24).
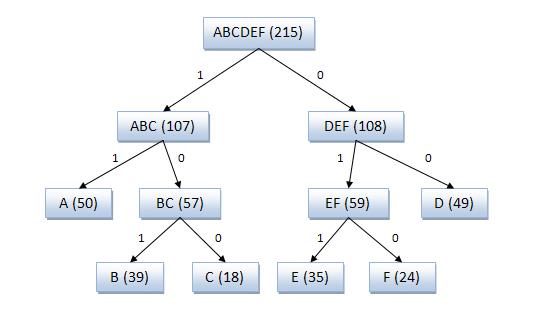
Рис.2. Кодовое дерево
Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.
2.4.2. КОД ХАФФМАНА
Этот метод кодирования состоит из двух основных этапов:
– построение оптимального кодового дерева;
– построение отображения «код – символ» на основе построенного дерева.
Алгоритм построения кода Хаффмана.
1. Подсчитываются вероятности ![]() появления символов
появления символов ![]() первичного алфавита в исходном тексте (если они не заданы заранее).
первичного алфавита в исходном тексте (если они не заданы заранее).
2. Символы первичного алфавита выписывают в порядке убывания вероятностей.
3. Последние два символа в упорядоченном списке объединяют в один и вставляют его в соответствующей позиции, предварительно удалив символы, вошедшие в объединение. Вероятность возникшего нового символа равна суммарной вероятности удаленных. Затем вставляют новый символ в список остальных на соответствующее место (повторяют ранжирование списка по вероятности).
4. Предыдущий шаг повторяют до тех пор, пока в списке остается более одного символа.
Этот процесс можно представить как построение дерева, корень которого — символ с вероятностью 1, получившийся при объединении символов последнего шага, два его предшественника - символы из предыдущего шага.
Каждые два элемента, стоящие на одном уровне, нумеруются: 0 или 1. Коды получаются из путей - от первого потомка корня и до листка. При декодировании можно использовать то же самое дерево: считывается по одной цифре и делается шаг по дереву, пока не достигается лист. Затем выводится символ, стоящий в листе, и производится возврат в корень.
Построение дерева Хаффмана
Бинарное дерево, соответствующее коду Хаффмана, называют деревом Хаффмана. Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева.
Общая схема построения дерева Хаффмана выглядит следующим образом.
1. Составляется список кодируемых символов.
2. Из списка выбирается 2 узла с наименьшим весом (под весом следует понимать частоту использования символа или вероятность его появления – чем чаще используется, тем больше весит ).
3. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов.
4. Удалим выбранные узлы из списка.
5. Добавим вновь сформированный узел к списку.
6. Если в списке больше одного узла, то повторить п.п. 2-6.
Пример построения кода и дерева Хаффмана
Рассмотрим на примере источника с алфавитом мощностью 9 , задаваемого множеством пар ![]() , метод кодирования по Хаффману. Конкретные значения этого множества представлены в табл. 4.
, метод кодирования по Хаффману. Конкретные значения этого множества представлены в табл. 4.
Таблица 4
| |
|
|
|
|
|
|
|
|
|
| |
0.20 |
0.15 |
0.15 |
0.12 |
0.10 |
0.10 |
0.08 |
0.06 |
0.04 |
Таблица 5
| |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Код. |
| |
0.20 |
|
11 |
|||||||
| |
0.15 |
001 |
||||||||
| |
0.15 |
011 |
||||||||
| |
0.12 |
010 |
||||||||
| |
0.10 |
101 |
||||||||
| |
0.10 |
100 |
||||||||
| |
0.08 |
0001 |
||||||||
| |
0.06 |
00001 |
||||||||
| |
0.04 |
00000 |
||||||||
В рисунке табл. 5 приведены все объединения, указанные в алгоритме Хаффмана. Нетрудно убедиться, что «дерево», изображенное на рис. 3, получено простым поворотом на ![]() рисунка табл. 5. Рассмотрим движение по ветвям дерева от корня к листьям. Договоримся, что при каждом повороте направо будем записывать «0», а при повороте налево - «1».
рисунка табл. 5. Рассмотрим движение по ветвям дерева от корня к листьям. Договоримся, что при каждом повороте направо будем записывать «0», а при повороте налево - «1».
|

Рис. 3. Схема реализации алгоритма Хафманна
При движении от корня к листу ![]() мы дважды «повернем» направо, поэтому такому символу припишем кодовое слово -11. При движении к листу
мы дважды «повернем» направо, поэтому такому символу припишем кодовое слово -11. При движении к листу ![]() мы один раз повернем направо, затем налево и потом снова направо. Это дает кодовое слово – 101. Процедуру определения кодовых слов без труда можно продолжить.
мы один раз повернем направо, затем налево и потом снова направо. Это дает кодовое слово – 101. Процедуру определения кодовых слов без труда можно продолжить.
Дерево Хаффмана в стандартном виде представлено на рис. 4. На нем каждому повороту направо или налево предыдущей схемы поставлены в соответствие стрелочки ![]() и
и ![]() .
.
![]()
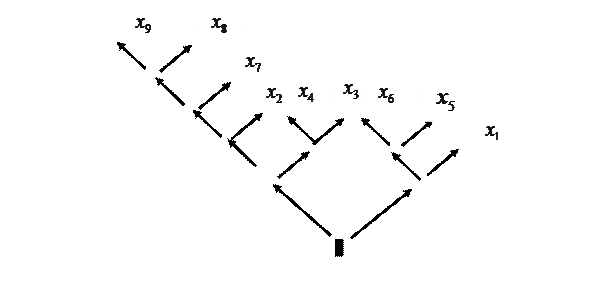
Рис. 4. Дерево Хаффмана для рассматриваемого примера
2.5. ЗАМЕЧАНИЯ ОТНОСИТЕЛЬНО АЛФАВИТА И ХАРАКТЕРИСТИК ОБОБЩЕННОГО ИСТОЧНИКА СООБЩЕНИЙ
Как отмечалось выше, источник сообщений и кодер источника часто объединяют вместе в некоторый обобщенный источник. Рассмотрим способ определения его характеристик.
Согласно изложенному в п.2.4., мощность нового алфавита равна двум (либо «0», либо «1»). А вот вероятности появления этих символов Вам предстоит вычислить. Как решить эту задачу?
Известны вероятности появления сообщений исходного алфавита, и Вы уже построили код Шеннона- Фано или Хаффмана. Согласно последнему можно рассчитать частоту появления «1» (или «0») в каждом кодовом слове. Известна и вероятность появления этого кодового слова. Так, в примере, рассмотренном выше, частота появления «1» при генерации ![]() –
– ![]() , а вероятность появления
, а вероятность появления ![]() -
- ![]() . Тогда вклад
. Тогда вклад ![]() в вероятность появления «1» равен
в вероятность появления «1» равен ![]() . Полная вероятность появления «1» в последовательности сообщений обобщенного источника может быть определена по формуле
. Полная вероятность появления «1» в последовательности сообщений обобщенного источника может быть определена по формуле 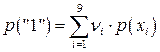 . Аналогично рассчитывается вероятность появления «0». Отличие полученных величин от
. Аналогично рассчитывается вероятность появления «0». Отличие полученных величин от ![]() характеризует степень отклонения кода от оптимального. Именно здесь кроется причина различия скорости передачи информации и пропускной способности канала при «оптимальном» кодировании.
характеризует степень отклонения кода от оптимального. Именно здесь кроется причина различия скорости передачи информации и пропускной способности канала при «оптимальном» кодировании.
2.6. Дискретные каналы связи
Канал называется дискретным по входу (выходу), если множество входных (выходных) сообщений конечно.
Неотъемлемым свойством любого реального канала связи является наличие в нем источников помех, шумов, искажений. В феноменологической модели канала связи воздействие шумов и помех на сигнал не детализируется, а лишь указывается вероятность того, что сигнал будет искажен на столько, что на приемном конце канала он будет воспринят как некоторый другой сигнал из возможного списка (из алфавита источника). Будем говорить, что дискретный канал – канал без памяти, если каждое сообщение в любой последовательности сообщений искажается в канале независимо от того, какие сообщения передавались ранее, до него. Говорят при этом, что межсимвольной интерференцией можно пренебречь.
Говорят, что дискретный канал без памяти задан, если заданы все условные вероятности ![]() , т.е. известна вероятность того, что переданное сообщение
, т.е. известна вероятность того, что переданное сообщение ![]() будет воспринято на приемном конце как
будет воспринято на приемном конце как ![]() .
.
Остановимся на одном моменте. Должны ли алфавиты входного и выходного устройства канала совпадать? Оказывается – нет! Например, в канале со стиранием выходной алфавит содержит, кроме символов входного алфавита, специальный символ стирания, который появляется на выходе дискретного канала, когда демодулятор не может с уверенностью принять решение в пользу одного из входных символов.
При выполнении работы
обратите внимание
на то, что мощность алфавита в кодере источника равна двум. Это значит, что матрица переходов ![]() содержит четыре элемента, тогда как заданы в таблицах только два из них. Недостающие элементы легко определить из условия
содержит четыре элемента, тогда как заданы в таблицах только два из них. Недостающие элементы легко определить из условия ![]() , выражающего тот факт, что какой-либо символ из допустимого множества
, выражающего тот факт, что какой-либо символ из допустимого множества ![]() обязательно появится на приемном конце канала связи.
обязательно появится на приемном конце канала связи.
Будем говорить, что канал зашумлен слабо, если величина ![]() близка к единице. Другими словами, правильное распознавание (
близка к единице. Другими словами, правильное распознавание (![]() было передано, и принимаемый сигнал был воспринят как
было передано, и принимаемый сигнал был воспринят как ![]() ) является практически достоверным событием. Если величина
) является практически достоверным событием. Если величина ![]() отличается от единицы значимо, то канал будем называть сильно зашумленным.
отличается от единицы значимо, то канал будем называть сильно зашумленным.
Если входной и выходной алфавиты совпадают и при ошибке в приеме вероятности появления любых ошибочных символов одинаковы, т.е.
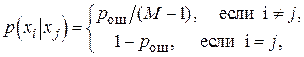 (5)
(5)
то канал называют симметричным. Если, кроме того, вероятность ошибки не зависит от времени, то говорят о стационарном симметричном канале. Наиболее просто выглядит модель стационарного симметричного канала без памяти, в котором ошибки при приеме различных символов являются статистически независимыми. Для такого канала вероятность получения ![]() ошибок при передаче
ошибок при передаче ![]() символов подчиняется биномиальному закону:
символов подчиняется биномиальному закону:
![]() . (6)
. (6)
Из этого выражения можно найти такие характеристики, как вероятность правильного приема блока из ![]() символов:
символов:
![]() (7)
(7)
и вероятность приема блока, содержащего хотя бы одну ошибку,
![]() . (8)
. (8)
2.7. ОПТИМАЛЬНОЕ РЕШАЮЩЕЕ ПРАВИЛО ВОССТАНОВЛЕНИЯ СИМВОЛА ПРИ ПРИЕМЕ ПО КРИТЕРИЮ МИНИМУМА ВЕРОЯТНОСТИ СРЕДНЕЙ ОШИБКИ
При приеме сигнала по зашумленному каналу возникает вопрос о том, какой реально символ был передан
, совпадает ли он с тем, что зафиксировано на приемном устройстве, или шумы и помехи исказили его «до неузнаваемости». Другими словами: приняли сигнал ![]() , а на самом деле передано было что? Понятно, что абсолютно достоверно восстановить переданное сообщение невозможно, однако вычислить наиболее вероятный вариант, используя метод максимального правдоподобия, – в наших силах.
, а на самом деле передано было что? Понятно, что абсолютно достоверно восстановить переданное сообщение невозможно, однако вычислить наиболее вероятный вариант, используя метод максимального правдоподобия, – в наших силах.
В работе нужно получить решающее правило - правило выбора переданного символа ![]() по принятому -
по принятому - ![]() , оптимальное по критерию минимума вероятности средней ошибки. Понятно, что этот
, оптимальное по критерию минимума вероятности средней ошибки. Понятно, что этот ![]() не истинно переданный символ, а лишь наиболее ожидаемый, наиболее вероятный. Поэтому мы будем обозначать его значком с «крышечкой» -
не истинно переданный символ, а лишь наиболее ожидаемый, наиболее вероятный. Поэтому мы будем обозначать его значком с «крышечкой» - ![]() .
.
Канал связи задается двумя множествами ![]() и
и ![]() . Первое определяет вероятность появления символа
. Первое определяет вероятность появления символа ![]() на входе канала, второе задает вероятности перехода – вероятность того, что будет принят символ
на входе канала, второе задает вероятности перехода – вероятность того, что будет принят символ ![]() , если реально был передан символ
, если реально был передан символ ![]() . Согласно методу правдоподобия нас будет интересовать такой
. Согласно методу правдоподобия нас будет интересовать такой ![]() , который доставляет максимум условной вероятности
, который доставляет максимум условной вероятности ![]() ,т.е.
,т.е. ![]() .
.
Заметим, что эта условная вероятность принципиально отличается от вероятности перехода, задающей канал связи. Она описывает вероятность при условии известного принятого символа , тогда как переходная вероятность задается при условии известного переданного символа . Однако эти вероятности связаны между собой известным соотношением
![]() , (9)
, (9)
которое можно переписать в виде
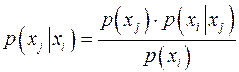 . (10)
. (10)
С максимальной достоверностью переданное сообщение может быть определено как
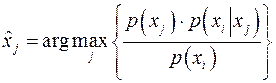 . (11)
. (11)
При этом вероятность ошибки в определении переданного символа при принятом символе ![]() будет минимальна и может быть найдена по формуле:
будет минимальна и может быть найдена по формуле:
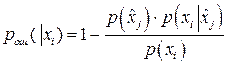 . (12)
. (12)
Если теперь вычислить среднюю ошибку, получаемую усреднением по всем возможным принимаемым символам, то вероятность ошибки будет равна:
 (13)
(13)
Из приведенного соотношения видно, что ошибка будет минимальна, если для каждого принятого символа ![]() мы будем выбирать такой символ
мы будем выбирать такой символ ![]() , что произведение
, что произведение ![]() будет принимать максимальную величину.
будет принимать максимальную величину.
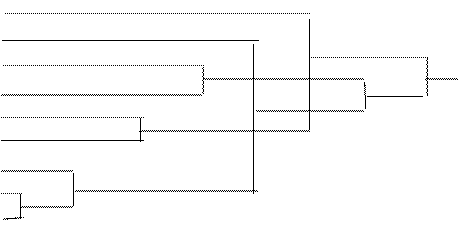
Описанное правило реализуем с помощью следующего алгоритма, проиллюстрированного приводимым ниже примером и рис.5.
Пусть вероятности передачи символов по каналу заданы вектором ![]() и матрицей переходных вероятностей
и матрицей переходных вероятностей ![]() :
:
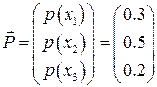
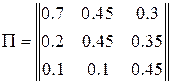 .
.
Построим фигуру, изображенную на рис.5
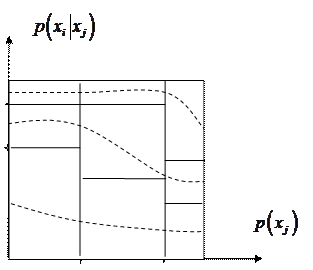 По оси абсцисс откладываются три отрезка, пропорциональные
По оси абсцисс откладываются три отрезка, пропорциональные ![]() ,
, ![]() и
и![]() соответственно. По оси ординат в каждой полосе откладываются условные вероятности
соответственно. По оси ординат в каждой полосе откладываются условные вероятности ![]() , моделирующие шум в канале. Очевидно, что площади образовавшихся прямоугольников будут пропорциональны вероятностям
, моделирующие шум в канале. Очевидно, что площади образовавшихся прямоугольников будут пропорциональны вероятностям ![]() .
.
Рис. 5
В соответствии с (13) для каждого ![]() - принятого символа, т.е. в каждой «строке», выделенной пунктирной линией на рис.5, надо выбрать такой прямоугольник, чья площадь максимальна. Его номер по оси абсцисс – j определит наиболее вероятный символ –
- принятого символа, т.е. в каждой «строке», выделенной пунктирной линией на рис.5, надо выбрать такой прямоугольник, чья площадь максимальна. Его номер по оси абсцисс – j определит наиболее вероятный символ – ![]() , который, скорее всего, был передан источником. Рассмотрим сначала первую (нижнюю) строку – случай приема символа
, который, скорее всего, был передан источником. Рассмотрим сначала первую (нижнюю) строку – случай приема символа ![]() . При переданном символе
. При переданном символе ![]() вероятность
вероятность ![]() , при
, при ![]() –
– ![]() , при
, при ![]() –
– ![]() . Совместная вероятность
. Совместная вероятность ![]() – 0.225 достигает наибольшее значение на паре
– 0.225 достигает наибольшее значение на паре ![]() , где
, где ![]() - принятый, а
- принятый, а ![]() - переданный символы. Это значит: принимая сигнал
- переданный символы. Это значит: принимая сигнал ![]() , полагайте, что был передан сигнал
, полагайте, что был передан сигнал ![]() . Разрешение кажущегося парадокса связано с тем, что вероятность передачи символа
. Разрешение кажущегося парадокса связано с тем, что вероятность передачи символа ![]() - 0.5 значимо больше вероятности передачи символа
- 0.5 значимо больше вероятности передачи символа ![]() - 0.3. В рассматриваемом нами примере решающее правило выглядит следующим образом:
- 0.3. В рассматриваемом нами примере решающее правило выглядит следующим образом: ![]() .
.
ЛИТЕРАТУРА
1. Колесник В.Д. и Полтырев Г.Ш. Курс теории информации. – М.: Наука, 1982.
2. Стратонович Р.Л. Теория информации. – М.: Сов. радио, 1975.
3. Котоусов А.С. Теория информации. – М.: Радио и связь, 2003.
|