Расчет статически неопределимой рамы методом сил
СОДЕРЖАНИЕ: Задача №5. Расчет статически неопределимой рамы методом сил Для статически неопределимой Е-образной рамы с одной скользящей и двумя неподвижными опорами используя метод сил, формулу Мора и правило Верещагина необходимо определить реакции опор и построить эпюры моментов, поперечных и продольных силЗадача №5.
Расчет статически неопределимой рамы методом сил
Для статически неопределимой Е-образной рамы с одной скользящей и двумя неподвижными опорами используя метод сил, формулу Мора и правило Верещагина необходимо определить реакции опор и построить эпюры моментов, поперечных и продольных сил
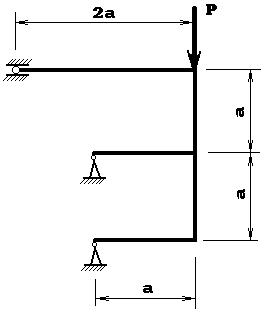
Построить эпюры M, Q и N.
Решение
Данная система дважды статически неопределима, так как рама прикреплена пятью связями, а уравнений статики для их определения – три. Выбираем основную систему путем отбрасывания лишних связей и заменой их неизвестными усилиями Х1 и Х2 . Фактически Х1 будет являться реакцией опоры С, а Х2 – вертикальной составляющей реакции опоры В.
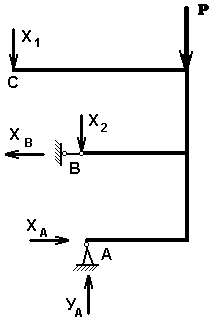
Составляем систему канонических уравнений метода сил:
![]() d11
Х1
+ d12
Х2
+ D1Р
= 0;
d11
Х1
+ d12
Х2
+ D1Р
= 0;
d21 Х1 + d22 Х2 + D2Р = 0.
Для определения коэффициентов при неизвестных и свободных членах необходимо построить эпюры изгибающих моментов поочередно для каждой силы.
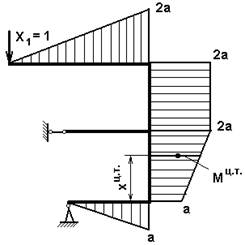
Эпюра единичных изгибающих моментов от единичной силы Х1
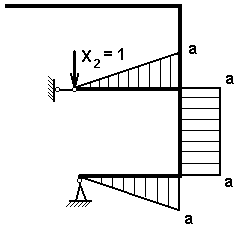
Эпюра единичных изгибающих моментов от единичной силы Х2
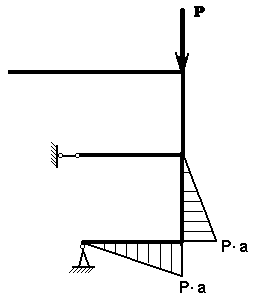
Грузовая эпюра от заданной нагрузки – силы Р.
Подсчитываем коэффициенты по формуле Мора используя правило Верещагина:
![]()
где ![]() – величина изгибающего момента единичной эпюры Хj
в точке, где расположен центр тяжести фигуры, образованной единичной эпюрой Хi
;
– величина изгибающего момента единичной эпюры Хj
в точке, где расположен центр тяжести фигуры, образованной единичной эпюрой Хi
;
![]() – площадь фигуры, образованной единичной эпюрой Хi
.
– площадь фигуры, образованной единичной эпюрой Хi
.
Например, для трапециевидного участка длиной L и размерами сторон м и М единичной эпюры Х1 находим координату центра тяжести для трапеции:
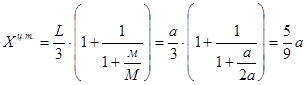 ;
;
Далее находим значение Мц.т. в этой точке для всех эпюр.
– для эпюры Х1 это будет:
![]() ,
,
– для эпюры Х2 в любой точке данного участка М равно а, следовательно:
![]()
– для эпюры Р это будет:
![]()
Соответственно площади эпюр на данном участке будут равны:
![]()
![]()
![]()
Аналогичным образом находим составляющие уравнения Мора для других, более простых участков и вычисляем требуемые коэффициенты:
![]()
![]()
![]()
![]()
![]()
Подставив найденные коэффициенты в систему канонических уравнений и сократив на ![]() и а3
получим систему двух уравнений с двумя неизвестными:
и а3
получим систему двух уравнений с двумя неизвестными:
![]()
![]()
![]() Х1
+
Х1
+ ![]() Х2
+ Р = 0; 56Х1
+ 11Х2
+ 6Р = 0;
Х2
+ Р = 0; 56Х1
+ 11Х2
+ 6Р = 0;
![]() Х1
+
Х1
+ ![]() Х2
+
Х2
+ ![]() Р = 0.11Х1
+ 10Х2
+ 7Р = 0;
Р = 0.11Х1
+ 10Х2
+ 7Р = 0;
Вычитая из первого уравнения второе, получим более простое выражение, из которого выразим Х2 и подставим затем во второе уравнение;
45Х1 + Х2 – Р = 0;®Х2 = Р – 45Х1 ;
11 Х1 + 10Р – 450 Х1 + 5Р = 0;
Х1
= ![]() Р = 0,034Р;
Р = 0,034Р;
Х2
= Р – ![]() Р = –
Р = –![]() Р = –0,538Р;
Р = –0,538Р;
Найдя значения неизвестных усилий Х1 и Х2 , обратимся к основной системе и найдем ХА , УА и ХВ .
S У = 0;
УА – Х1 – Х2 – Р = 0;
УА = Х1 + Х2 + Р = 0,034Р – 0,538Р + Р = 0,496Р;
S МА = 0;
Х1 а + ХВ а – Ра = 0;
ХВ = Р – Х1 = 0,966Р;
S Х = 0;
ХА – ХВ = 0;
ХА = ХВ = 0,966Р;
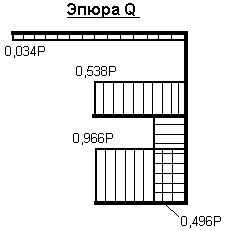
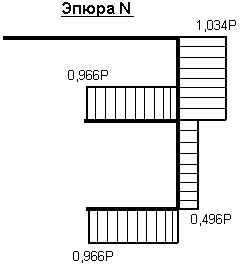
Зная значения всех усилий, действующих на раму, строим эпюры М, Q и N: