Расчет структурной схемы системы автоматического управления
СОДЕРЖАНИЕ: Определение передаточной функции разомкнутой системы, стандартной формы ее записи и степени астатизма. Исследование амплитудно-фазовой, вещественной и мнимой частотных характеристик. Построение годографа АФЧХ. Алгебраические критерии Рауса и Гурвица.КУРСОВАЯ РАБОТА
по дисциплине:Теория автоматического управления
Уфа 2011
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Вариант 16
| Схема | k1 | k2 | k3 | k4 | k5 | T1 | T2 | T3 | T4 | T5 | |
| (а) | 4 | 1.5 | 4 | 2 | 0.7 | 0.4 | 0.3 | 0.5 | 0.15 | 0.9 | 0.5 |
Схема а:
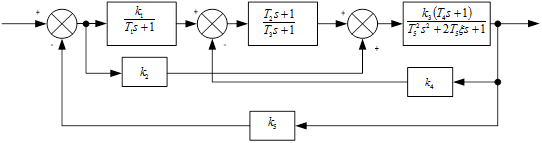
Для структурной схемы САУ, соответствующей выбранному варианту, выполнить следующие действия:
1) Определить передаточную функцию разомкнутой системы, привести ее к стандартной форме записи. Определить степень астатизма системы.
2) Определить амплитудно-фазовую, вещественную и мнимую частотные характеристики.
3) Построить годограф АФЧХ разомкнутой системы.
4) Найти выражения для асимптотической ЛАЧХ и ЛФЧХ разомкнутой системы.
5) Построить в масштабе ЛАЧХ и ЛФЧХ разомкнутой системы.
6) Определить устойчивость замкнутой САР с помощью критерия Найквиста и логарифмических частотных характеристик.
7) Найти запасы устойчивости системы по фазе и амплитуде.
8) Записать выражение для передаточной функции замкнутой системы и проверить выводы пункта 6 с помощью алгебраических критериев Рауса и Гурвица.
9) Проверить выводы пункта 6 с помощью частотного критерия Михайлова.
10) Найти коэффициенты С0 , С1 , С2 ошибок системы.
11) Построить с помощью ЭВМ переходную функцию замкнутой системы и оценить основные показатели качества регулирования (перерегулирование, и время регулирования) в системе.
передаточный астатизм амплитудный голограф
1. Передаточная функция разомкнутой системы
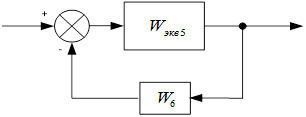
Упростим схему.
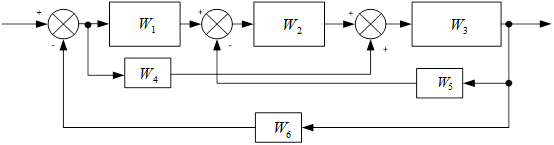
Где
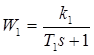 ;
; 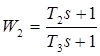 ;
; 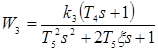 ;
; ![]() ;
; ![]() ;
; ![]() .
.
Перенесем сумматор.
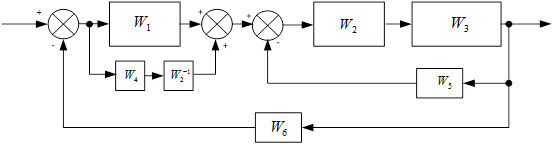
Затем упростим.
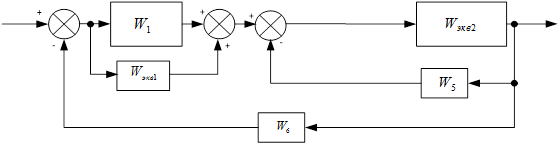
Где
![]() ;
; ![]()
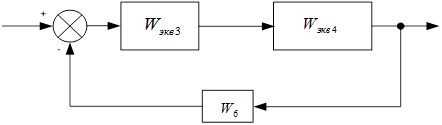
Где
![]() ;
; 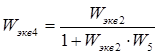
Где
![]()
![]() ;
;
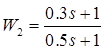 ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
![]() ;
;
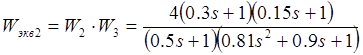 ;
;
![]()
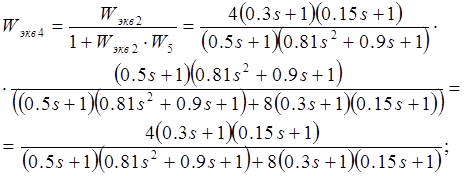
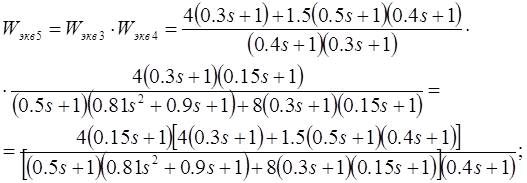
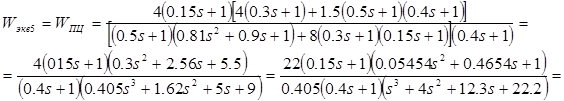

![]()
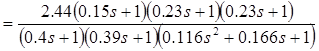
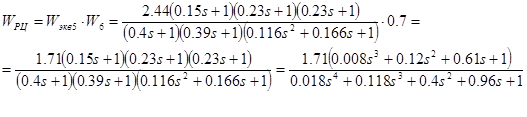
Степень астатизма =0. Коэффициент передачи К=1.71. Постоянные времени: Т1 =0.15, Т2 =0.23, Т3 =0.23, Т4 =0.4, Т5 =0.39, Т6 =0.34, =0.24.
2. Частотная передаточная функция системы (sj)
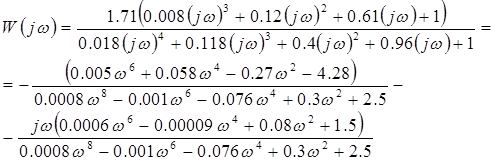
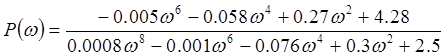
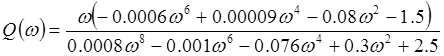
Особые точки АФЧХ приведены в таблице 1.
Таблица 1.
| 0 | 2,85 | ||
| P() | 1.71 | 0 | 0 |
| Q() | 0 | -2.46 | 0 |
3. Годограф АФЧХ разомкнутой системы
Годограф (рисунок 1) при =0 начинается на положительной вещественной полуоси. При через четвертый и третий квадранты стремиться к нулю. Пересекает при =0 вещественную ось в точке (1,71;j0) и при =2,85 пересекает мнимую ось в точке (0;-j2.46).
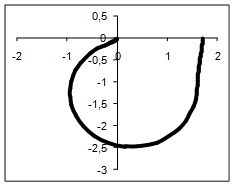
Рисунок 1.
4. Асимптотическая ЛАХ и ЛФХ
Асимптотическая ЛАХ:
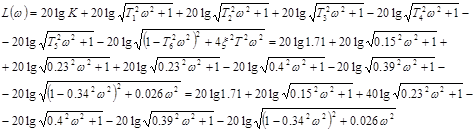
Асимптотическая ЛФХ:
![]()
![]()
5. Построение в масштабе ЛАХ и ЛФХ системы
1) Значение ЛАХ при =1 равно 20lgK, где К – коэффициент передачи разомкнутой системы. К=1,71, значит ЛАХ пересекает ось L() на уровне 4.66.
2) Степень астатизма системы =0, следовательно наклон самой низкочастотной асимптоты равен 0 дБ/дек.
3) Таблица значений сопрягаемых частот.
Таблица 2.
| Т | 0.4 | 0.39 | 0.34 | 0.23 | 0.23 | 0.15 |
| 2.5 | 2.56 | 2.94 | 4.35 | 4.35 | 6.67 | |
| Изменение наклона (дБ/дек) | -20 | -20 | -40 | +20 | +20 | +20 |
Асимптотическая ЛАХ, построенная от руки (схематично) по информации из таблицы 2 показана на рисунке 2.
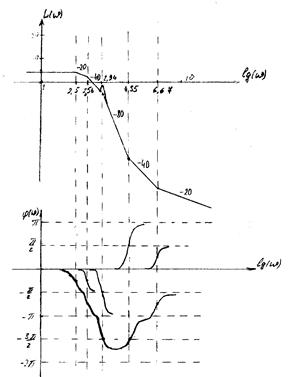
Рисунок 2.
На рисунке 3 показаны в масштабе ЛАХ и ЛФХ системы, построенные с помощью ЭВМ.
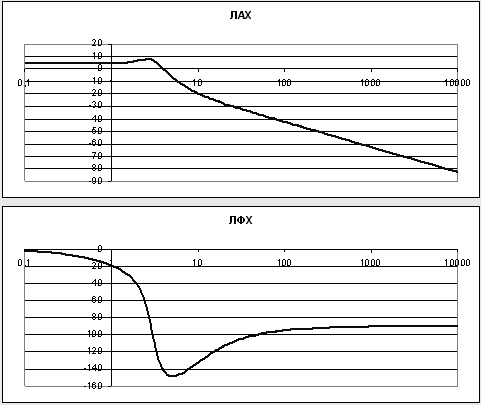
Рисунок 3.
6. Устойчивость замкнутой САУ с помощью критерия Найквиста и логарифмических частотных характеристик
Степень астатизма системы =0 и характеристический полином разомкнутой системы имеет все корни в левой половине комплексной плоскости, то критерий Найквиста будет следующим: Для того чтобы замкнутая САУ была устойчивой необходимо и достаточно, чтобы годограф амплитудно-фазовой характеристики разомкнутой системы не охватывал точку с координатами (-1; j0).
На рисунке 4 изображен годограф АФХ. Он не охватывает точку (-1; j0), следовательно, замкнутая система будет устойчивой.

Рисунок 4.
7. Запасы устойчивости по фазе и амплитуде
Как видно из рисунка 4 годограф не пересекает отрицательную вещественную полуось, следовательно, запас устойчивости по амплитуде 100%.
Рассчитаем запас устойчивости по фазе:
Найдем ср (частоту среза) из условия A()=1
![]()
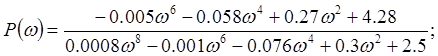
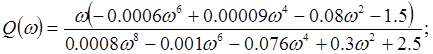
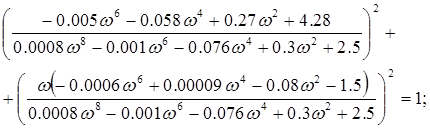
ср =3,924 с-1
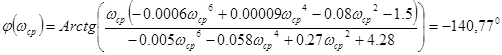
![]()
Таким образом запас по фазе составляет 39,230 .
Передаточная функция замкнутой системы может быть найдена по следующей формуле
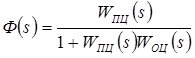
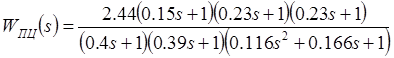
![]()
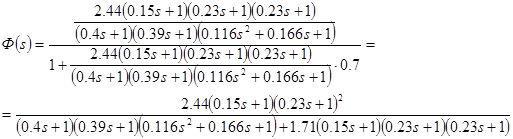
Характеристический полином системы:
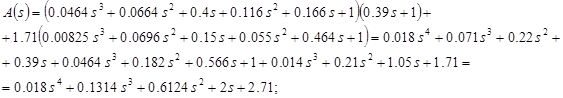
![]()
Определение устойчивости замкнутой системы методом Рауса.
![]()
Таблица Рауса.
| a0 | a2 | a4 | |
| a1 | a3 | a5 =0 | |
| C13 =a2 -3 a3 | C23 =a4 -3 a5 | C33 =a6 -3 a7 | 3 =a0 /a1 |
| C14 =a3 - 4 C23 | C24 =a5 - 4 C33 | C34 =0 | 4 =a1 /C13 |
| C15 =C23 -5 C24 | C25 =C33 -5 C34 | C35 =0 | 5 =C13 /C14 |
| C16 =C24 -6 C25 | C26 =C34 -6 C35 | C36 =0 | 6 =C14 /C15 |
Заполним таблицу.
| 0.018 | 0.612 | 2.71 | |
| 0.1314 | 2 | 0 | |
| C13 =0.3384 | C23 =2.71 | C33 =0 | 3 =0.137 |
| C14 =0.948 | C24 =0 | C34 =0 | 4 =0.388 |
| C15 =2.71 | C25 =0 | C35 =0 | 5 =0.357 |
| C16 =0 | C26 =0 | C36 =0 | 6 =0.34 |
Все элементы первого столбца таблицы имеют один и тот же знак, следовательно, характеристический полином замкнутой системы имеет корни только в левой половине комплексной плоскости. Замкнутая САУ устойчива.
Определение устойчивости замкнутой системы методом Гурвица.
Построим определители Гурвица
![]()
![]()
![]()
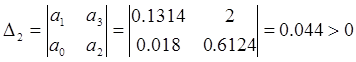
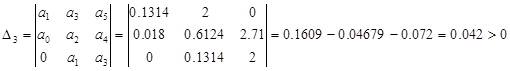
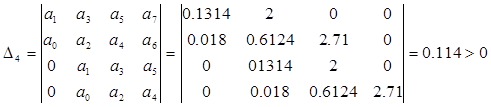
Все определители Гурвица положительны, следовательно, характеристический полином замкнутой системы имеет корни только в левой половине комплексной плоскости. Замкнутая САУ устойчива.
8. Определение устойчивости замкнутой системы с помощью частотного критерия Михайлова
Характеристический полином системы
![]()
sj
![]()
Вещественная функция Михайлова:
![]() .
.
Мнимая функция Михайлова:
![]()
Решим уравнения
![]() ;
;![]() .
.
![]() ,
,
Учитываем корни 0
![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
![]() ;
; ![]() ;
; ![]() .
.
Построим таблицу
| 0 | 2.88 | 3.9 | 5.36 | |
| Re() | 2.71 | 0 | -2.44 | 0 |
| Im() | 0 | 3 | 0 | -9.57 |
Годограф Михайлова (в схематичном виде) представлен на рисунке 5.
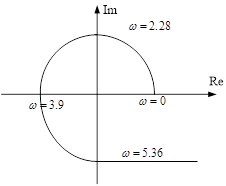
Рисунок 5.
Критерий Михайлова: Замкнутая САУ будет устойчивой тогда и только тогда, когда годограф Михайлова, при изменении частоты от 0 до + начинаясь на положительной действительной полуоси последовательно и нигде не обращаясь в 0 пересекает n квадрантов комплексной плоскости (где n – порядок характеристического полинома САУ).
В данном случае годограф соответствует критерию Михайлова, значит замкнутая САУ устойчива.
9. Коэффициенты ошибок системы
Передаточная функция ошибки будет иметь вид
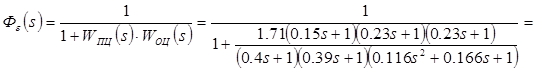
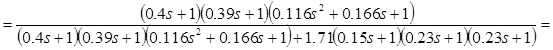
![]()
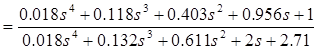
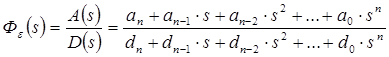
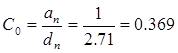
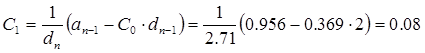
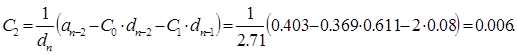
10. Переходная функция САУ
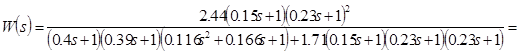
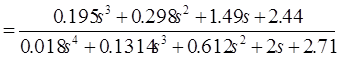
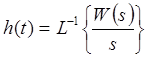
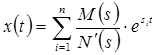
![]()
![]()
![]()
Найдем корни N(s):
![]()
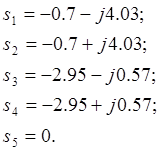
Получим следующее:
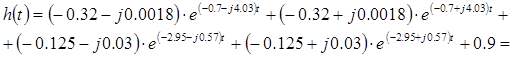
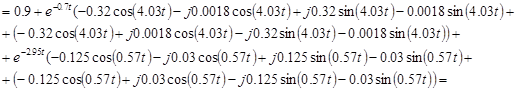
![]()
Построим график с помощью ЭВМ.
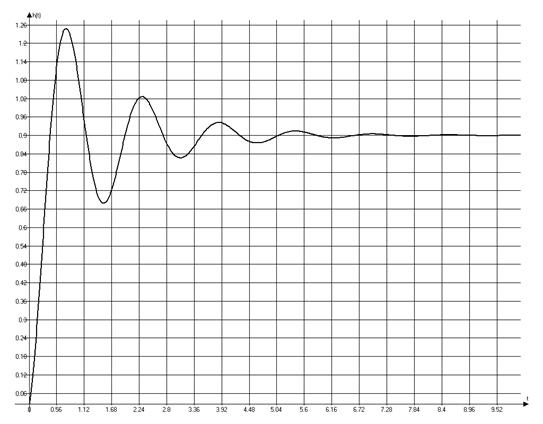
График переходной функции.
Из графика видно, что время регулирования tp 3.29с, а перерегулирование
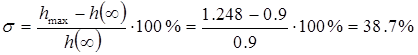 .
.