Расчет цифровых фильтров с бесконечными импульсными характеристиками
СОДЕРЖАНИЕ: Расчет аналогового фильтра-прототипа низких частот. Получение дискретизированного аналога фильтра Чебышева при помощи метода билинейного z-преобразования. Влияние усечения коэффициентов передаточной функции на амплитудно-частотную характеристику.Белорусский Государственный Университет
Информатики и Радиоэлектроники
Кафедра электронных вычислительных средств
Отчёт по лабораторной работе
Расчет цифровых фильтров с бесконечными импульсными характеристиками
Выполнила:
Студентка гр. 610701
Лыпка Ю.А.
Проверил:
Родионов М.М.
Минск 2009
Цель работы: Расчёт БИХ-фильтров с различными аппроксимациями идеальной АЧХ в пакете Matlab и изучение их свойств.
Задание №1: Рассчитайте аналоговый фильтр-прототип НЧ в соответствии с вариантом (вариант №8). Для полученного фильтра постройте его АЧХ, ФЧХ а также диаграмму нулей и полюсов.
Фильтр Чебышева 1 рода, 4 порядка.
n=4;
Rp=1;
[z,p,k]=cheb1ap(n,Rp);
[b,a]=zp2tf(z,p,k);
figure(1);
zplane(z,p);
title(Lowpass Chebyshev Filter);
figure(2);
subplot(211);
[h,w]=freqs(b,a);
plot(w,abs(h),r);
title(Amplitude response);
subplot(212);
plot(w,unwrap(angle(h)),r);
title(Phase response);
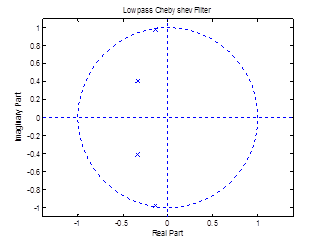
Рисунок 1 – Диаграмма нулей и полюсов
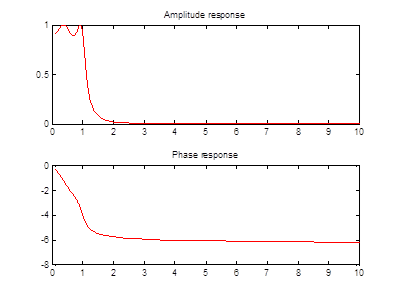
Рисунок 2 – АЧХ и ФЧХ фильтра НЧ вида Чебышева 1 рода
Задание №2: Преобразовать полученный фильтр- прототип в фильтр заданного вида с требуемыми частотами среза (Вариант 8- 650Гц). Постройте графики АЧХ, ФЧХ и диаграмму нулей и полюсов.
fs=650;% частота среза
[b1,a1]=lp2lp(b,a,fs);
[z1,p1,k1]=tf2zp(b1,a1);
figure(3);
zplane(z1,p1);
title(Lowspass Chebyshev Filter);
figure(4);
subplot(211);
[h,w]=freqs(b1,a1);
plot(w,abs(h),m);
title(Amplitude response);
subplot(212);
plot(w,unwrap(angle(h)),m);
title(Phase response);

Рисунок 3 – Диаграмма нулей и полюсов
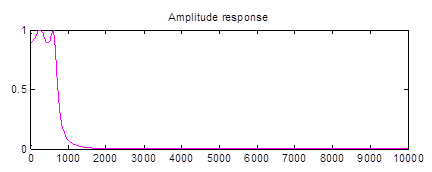
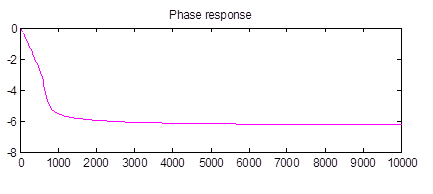
Рисунок 4 – АЧХ и ФЧХ фильтра НЧ вида Чебышева 1 рода
Задание №3: Используя функцию Matlab bilinear, которая реализует метод билинейного z- преобразования, получите дискретизированный аналог фильтра из предыдущего задания. Постройте АЧХ, ФЧХ, групповую задержку и диаграмму нулей и полюсов полученного фильтра.
Fs=2600;
[zt,pt,kt]=bilinear(z1,p1,k1,Fs);
[bt,at]=zp2tf(zt,pt,kt);
figure(5)
zplane(zt,kt);
title(Bilinear Conversion);
figure(6);
subplot(311);
[h,w]=freqz(bt,at)
plot(w,abs(h),g);
subplot(312);
plot(w,unwrap(angle(h)),g);
subplot(313);
grpdelay(bt,at,64,Fs);%%%групповая задержка
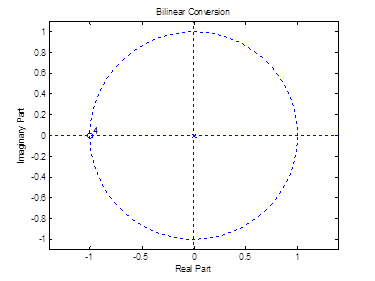
Рисунок 5 – Диаграмма нулей и полюсов
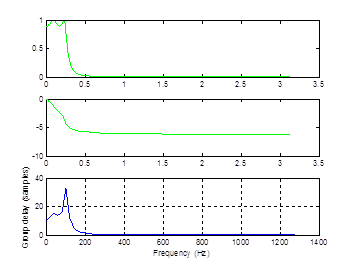
Рисунок 6 – АЧХ , ФЧХ и групповая задержка фильтра
Задание №4: Рассчитайте цифровой ФВЧ с параметрами заданными для каждого варианта. Определить какой порядок будут иметь разные типы фильтров. Сравнить эффективность аппроксимаций при более жестких и более мягких требованиях к АЧХ.
close all;
clear all;
clear all;
Wp = 0.4; % нормированная граничная частота подавления
Ws = 0.7; % нормированная граничная частота пропускания
Rp = 0.5; % допустимая неравномерность в полосе пропускания
Rs = 70; % минимальное затухание в полосе подавления
%%%%%%%%%%%%%%Фильтр Баттерворта%%%%%%%%%%%%
[n1, Wn1] = buttord(Wp, Ws, Rp, Rs);
sprintf( battervorta - %d,n1)
[z,p,k] = butter(n1,Wn1,high);
[b,a]=zp2tf(z,p,k);
figure;
zplane(z,p);
figure;
title(battervorta);
freqs(z,p);
%%%%%%%%%%%%%%Фильтр Чебышева 1 рода%%%%%%%%
[n2, Wn2] = cheb1ord(Wp, Ws, Rp, Rs);
[z,p,k] = cheby1(n2,Rp,Wn2,high);
[b,a]=zp2tf(z,p,k);
figure;
zplane(z,p);
figure;
freqs(z,p);
%%%%%%%%%%%%Фильтр Чебышева 2 рода%%%%%%%%%%
[n3, Wn3] = cheb2ord(Wp, Ws, Rp, Rs);
[z,p,k] = cheby2(n3,Rs,Wn3,High);
[b,a]=zp2tf(z,p,k);
figure;
zplane(z,p);
figure;
freqs(z,p);
%%%%%%%%%%%Фильтр Эллиптический%%%%%%%%%%%%%
[n4, Wn4] = ellipord(Wp, Ws, Rp, Rs);
[z,p,k] = ellip(n4,Rp,Rs,Wn4,high);
[b,a]=zp2tf(z,p,k);
figure;
zplane(z,p);
figure;
freqs(z,p);
sprintf( chebysheva1 - %d,n2)
sprintf( chebysheva2 - %d,n3)
sprintf( elipticheskiy - %d,n4)

Рисунок 7– Диаграмма нулей и полюсов фильтра Баттерворта
 .
.
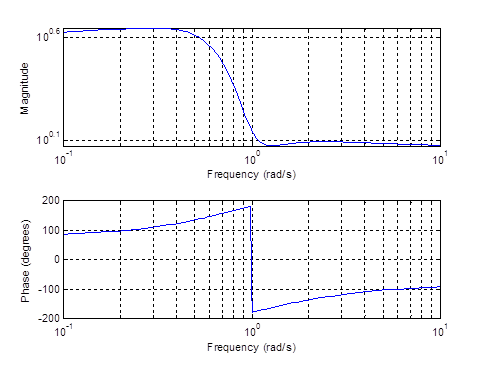
Рисунок 8– АЧХ , ФЧХ фильтра Баттерворта
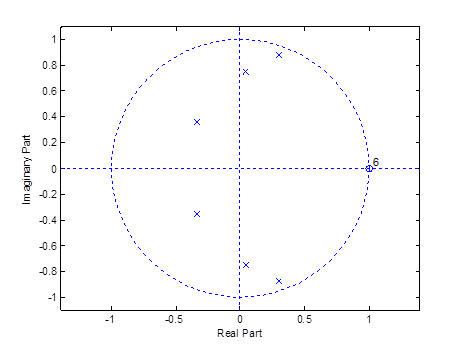
Рисунок 9– Диаграмма нулей и полюсов фильтра Чебышева 1 рода
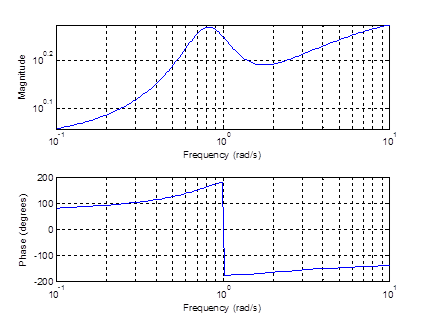
Рисунок 10– АЧХ , ФЧХ фильтра Чебышева 1 рода
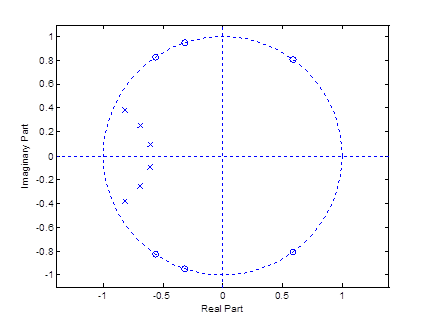
Рисунок 11– Диаграмма нулей и полюсов фильтра Чебышева 2 рода
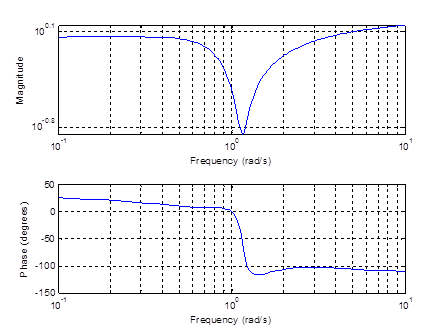
Рисунок 12– АЧХ , ФЧХ фильтра Чебышева 2 рода
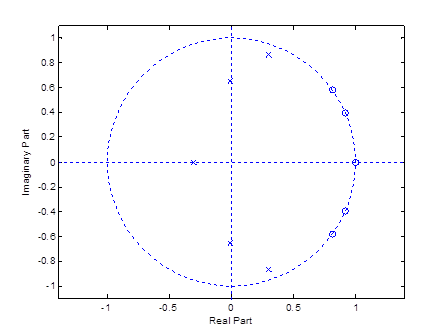
Рисунок 13– Диаграмма нулей и полюсов эллиптического фильтра
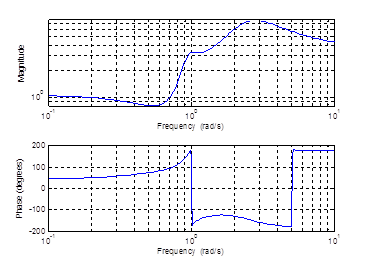
Рисунок 14– АЧХ , ФЧХ эллиптического фильтра
Задание №5: Исследуйте как скажется на АЧХ и ФЧХ фильтров из заданий 1-3 усечение коэффициентов передаточной функции до четырёх десятичных разрядов. До двух десятичных разрядов.
close all;
clear all;
n = 4;
fs = 1000;
fc = 300;
Rp = 1;
Rs = 70;
Wn = fc * 2 / fs;
%%%%%%%%%%%%Butterworth%%%%%%%%%%%
figure;
[b, a] = butter(n, Wn);
[h, f] = freqz(b, a, 1024, fs);
b = round(b * 10000) / 10000;
a = round(a * 10000) / 10000;
[h2, f] = freqz(b, a, 1024, fs);
b = round(b * 1000) / 1000;
a = round(a * 1000) / 1000;
[h3, f] = freqz(b, a, 1024, fs);
b = round(b * 100) / 100;
a = round(a * 100) / 100;
[h4, f] = freqz(b, a, 1024, fs);
subplot(211);
plot(f, 20 * log10(abs(h)), k);
hold on;
plot(f, 20 * log10(abs(h2)), g);
plot(f, 20 * log10(abs(h3)), b);
plot(f, 20 * log10(abs(h4)), r);
legend(Ideal, 4 categories, 3 categories, 2 categories);
grid on;
title(Amlitude response);
ylabel(Butterworth);
subplot(212);
plot(f,angle(h), k);
hold on;
plot(f,angle(h2), g);
plot(f,angle(h3), b);
plot(f,angle(h4), r);
grid on;
title(Phase response);
ylabel(Butterworth);
%%%%%%%%%%%%Chebyshev1%%%%%%%%%%%
figure;
[b, a] = cheby1(n, Rp, Wn);
[h, f] = freqz(b, a, 1024, fs);
b = round(b * 10000) / 10000;
a = round(a * 10000) / 10000;
[h2, f] = freqz(b, a, 1024, fs);
b = round(b * 1000) / 1000;
a = round(a * 1000) / 1000;
[h3, f] = freqz(b, a, 1024, fs);
b = round(b * 100) / 100;
a = round(a * 100) / 100;
[h4, f] = freqz(b, a, 1024, fs);
subplot(211);
plot(f, 20 * log10(abs(h)), k);
hold on;
plot(f, 20 * log10(abs(h2)), g);
plot(f, 20 * log10(abs(h3)), b);
plot(f, 20 * log10(abs(h4)), r);
legend(Ideal, 4 categories, 3 categories, 2 categories);
grid on;
title(Amlitude response);
ylabel(Chebyshev1);
subplot(212);
plot(f,angle(h), k);
hold on;
plot(f,angle(h2), g);
plot(f,angle(h3), b);
plot(f,angle(h4), r);
grid on;
title(Phase response);
ylabel(Chebyshev1);
%%%%%%%%%%%%Elliptic%%%%%%%%%%%%%
figure;
[b, a] = ellip(n, Rp, Rs, Wn);
[h, f] = freqz(b, a, 1024, fs);
b = round(b * 10000) / 10000;
a = round(a * 10000) / 10000;
[h2, f] = freqz(b, a, 1024, fs);
b = round(b * 1000) / 1000;
a = round(a * 1000) / 1000;
[h3, f] = freqz(b, a, 1024, fs);
b = round(b * 100) / 100;
a = round(a * 100) / 100;
[h4, f] = freqz(b, a, 1024, fs);
subplot(211);
plot(f, 20 * log10(abs(h)), k);
hold on;
plot(f, 20 * log10(abs(h2)), g);
plot(f, 20 * log10(abs(h3)), b);
plot(f, 20 * log10(abs(h4)), r);
legend(Ideal, 4 categories, 3 categories, 2 categories);
grid on;
title(Amlitude response);
ylabel(Elliptic);
subplot(212);
plot(f,angle(h), k);
hold on;
plot(f,angle(h2), g);
plot(f,angle(h3), b);
plot(f,angle(h4), r);
grid on;
title(Phase response);
ylabel(Elliptic);
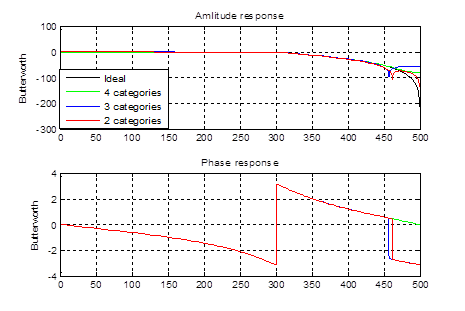
Рисунок 15 – АЧХ и ФЧХ фильтра Баттерворта
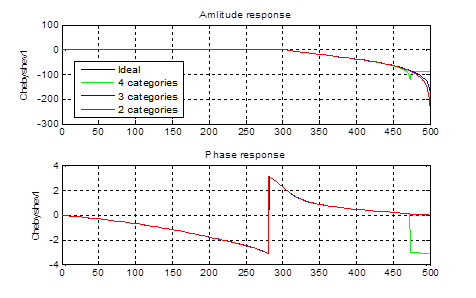
Рисунок 16 – АЧХ и ФЧХ фильтра Чебышева 1 рода
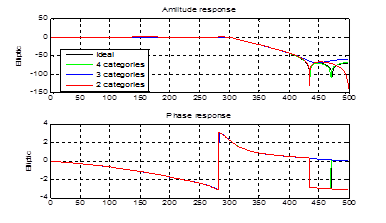
Рисунок 17 – АЧХ и ФЧХ эллиптического фильтра
Вывод: В результате выполненной лабораторной работы, были изучены фильтры НЧ и ВЧ и их типы. Программирование их в Matlab. Изучен метод билинейного z- преобразования для перевода фильтра из ВЧ в НЧ. Увидели, что при усечение коэффициентов происходит пропускание ненужных нам частот.