Расчет вала при совместном действии изгиба и кручения по гипотезам прочности
СОДЕРЖАНИЕ: Совместные действия изгиба и кручения, расчет с применением гипотез прочности. Значение эквивалентного момента по заданным координатам. Реакция опор в вертикальной и горизонтальной плоскости. Эпюра крутящихся, изгибающихся и вращающихся моментов.Костромская Государственная Сельскохозяйственная Академия
Кафедра: Детали машин
Методическое пособие и задачи для самостоятельного решения по курсу ПРИКЛАДНАЯ МЕХАНИКА
Раздел: Сопротивление материалов
Тема: РАСЧЕТ ВАЛА ПРИСОВМЕСТНОМ ДЕЙСТВИИ ИЗГИБА И КРУЧЕНИЯ ПО ГИПОТЕЗАМ ПРОЧНОСТИ.
Составил: доцент Комаров Н.В.
Кострома 2003
Для решения задания необходимо усвоить тему: Гипотезы прочности и их применение, т.к в задачах рассматриваются совместные действия изгиба и кручения и расчет производится с применением гипотез прочности.
Условие прочности в этом случае имеет вид
sэк в = Мэк в / Wz [s]
Мэк в - так называемый эквивалентный момент
По гипотезе наибольших касательных напряжений (III - гипотеза прочности)
Мэк в III = (Ми 2 + Тк 2 ) 1/2
По гипотезе потенциальной энергии формоизменения (V - гипотезе прочности)
Мэк в V = (Ми 2 + 0.75 Тк 2 ) 1/2
В обеих формулах Т - наибольший крутящий момент в поперечном сечении вала Ми - наибольший суммарный изгибающий момент, его числовое значение равно геометрической сумме изгибающих моментов, возникающих в данном сечении от вертикально и горизонтально действующих внешних сил, т.е.
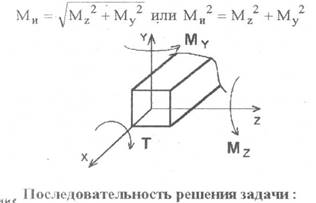
1. Привести действующие на вал нагрузки к его оси, освободить вал от опор, заменив их действия реакциями в вертикальных и горизонтальных плоскостях
2. По. заданной мощности Р и угловой скорости w определить вращающие моменты действующие на вал.
3. Вычислить нагрузки F1 , Fr 1 , F2 , Fr2 приложенные к валу.
4. Составить уравнения равновесия всех сил, действующих на вал, отдельно в вертикальной плоскости и отдельно в горизонтальной плоскости и определить реакции опор в обеих плоскостях.
5. Построить эпюру крутящих моментов.
6. Построить эпюру изгибающих моментов в вертикальной и горизонтальной плоскостях (эпюры Mz и My ) .
7. Определить наибольшее значение эквивалентного момента:
Мэк в III = (Мz 2 + My 2 + Тк 2 ) 1/2 или
Мэк в V = (Мz 2 + My 2 + 0.75 Тк 2 ) 1/2
8. Приняв sэк в = [s] определить требуемый осевой момент сопротивления
Wz = М эк в /[s]
9. Учитывая, что для бруса сплошного круглого сечения
Wи = p*dв 3/ 32 » 0.1* dв 3
определяем диаметр его d по следующей формуле:
d (32* М эк в / p*[s]) 1/3 » (М эк / 0.1 [s]) 1/3
Пример: Для стального вала постоянного поперечного сечения с двумя зубчатыми колесами, передающего мощность Р = 15 кВт при угловой скорости w =30 рад/с, определить диаметр вала по двум вариантам:.
а) Используя, III-гипотезу прочности
б) Используя, V - гипотезу прочности
Принять [s] =160МПа, Fr 1 = 0.4 F1 , Fr 2 = 0.4 F2
Составляем расчетную схему вала: Т1 =Т5 , где Т1 и Т2 - скручивающие пары, которые добавляются при параллельном переносе сил F1 и F2 на ось вала
Определяем вращающий момент действующий на вал:
Т1 = Т2 = Р/w = 0,5*103 Нм = 0,5 кНм
Вычисляем нагрузку приложенную к валу
F1 = 2*T1/ d1 = 2*0.5*103/ 0.1 = 104 H = 10kH
F2 = 2*T2/ d2 = 2*0.5*103/ 0.25 = 4*103 H = 4kH
Fr1 = 0.4*103 = 4 kH Fr2 = 0.4*4 = 1.6 kH
Определяем реакции опор в вертикальной плоскости YOX (рис б)
Ma = - Fr1 AC - Fr2 AD + RBY *AB = 0
RBY = Fr1 AC + Fr2 AD / AB = 4*0.05 + 1.6*0.25/0.3 = 2 kH
MB = - RAY *AB + Fr1 *BC + Fr2 *DB = 0
RAY = Fr1 *BC + Fr2 *DB / AB = 4*0.25 + 1.6*0.05/03 = 3.6 kH
Проверка:
Y = RAY - Fr1 - Fr2 + RBY = 2-4-1.6+3.6 = 0
Y = 0, следовательно RAY и RBY найдены правильно
Определим реакции опор в горизонтальной плоскости ХОZ (рис б)
MA = F1 AC - F2 AD - RBz *AB = 0
RBz = F1 AC - F2 AD / AB = 10*0.05 - 4*0.25/0.3 = - 1.66 kH
Знак минус указывает, что истинное направление реакции RBz противоположно выбранному (см. рис. б)
MB = RAz *AB - F1 *CB + F2 *DB = 0
RAz = F1 *CB - F2 *DB / AB = 10*0.25 - 4*0.05/0.3 = 7.66 kH
Проверка:
Z = RAz - F1 + F2 - RBz = 7.66-10+4-1.66 = 0
Z = 0, следовательно реакции RAz и RBz найдены верно.
Строим эпюру крутящих моментов Т (рис в).
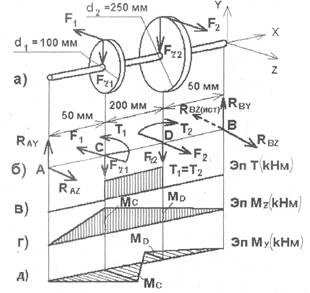
Определяем ординаты и строим эпюры изгибающих моментов Mz в вертикальной плоскости (рис. г и д) и Мy - в горизонтальной плоскости.
МCz = RAy *AC = 3.6*0.05 = 0.18 kHм
МDz = RAy *AD - Fr1 *CD = 3.6*0.25 - 4*0.2 = 0.1 kHм
МCy = RAz *AC = 7.66*0.05 = 0.383 kHм
МDy = RAz *AD - F1 *CD = 7.66*0.25 - 10*0.2 = - 0.085 kHм
Вычисляем наибольшее значение эквивалентного момента по заданным координатам так как в данном примере значение суммарного изгибающего момента в сечений С больше, чем в сечении D, то сечение С и является опасным. Определяем наибольший суммарный изгибающий момент в сечении С.
Ми С = (МС z 2 + MCy 2 ) 1/2 = (0.182 + 0.3832 ) 1/2 = 0.423 kHм
[Ми D = (МDz 2 + MDy 2 ) 1/2 = (0.12 + 0.0852 ) 1/2 = 0.13 kHм]
Эквивалентный момент в сечении C по III и V гипотезе прочности
Мэк в III = (Мz 2 + My 2 + Тк 2 ) 1/2 = (0182 + 0.3832 +0.52 ) 1/2 =
= 0.665 kHм
Мэк в V = (Мz 2 + My 2 + 0.75 Тк 2 ) 1/2 =
= (0.182 +0.3832 +0.75*0.52 ) 1/2 = 0.605 kHм
Определяем требуемые размеры вала по вариантам III и V гипотез прочности.
dIII = (Мэк в III / 0.1*[s]) 1/2 = (0.655*103/ 0.1*160*106 ) 1/2 =
= 3.45*10-2 (м) = 34.5 (мм)
dVI = (Мэк в V / 0.1*[s]) 1/2 = (0.605*103/ 0.1*160*106 ) 1/2 =
= 3.36*10-2 (м) = 33.6 (мм)
Принимаем диаметр вала согласно стандартного ряда значений d=34 мм
Из условия прочности рассчитать необходимый диаметр вала постоянного поперечного сечения, с двумя зубчатыми колёсами, предающего мощность Р, при заданной угловой скорости.
Принять [s] =160МПа, Fr 1 = 0.4 F1 , Fr 2 = 0.4 F2 (Все размеры указаны на рисунках)
| № задачи | вариант | Р, кВт | w, рад/с | № задачи | вариант | Р, кВт | w, рад/с |
| 0 | 0 | 6 | 22 | 1 | 0 | 3 | 25 |
| 1 | 8 | 36 | 1 | 8 | 48 | ||
| 2 | 10 | 40 | 2 | 10 | 50 | ||
| 3 | 9 | 30 | 3 | 12 | 40 | ||
| 4 | 3 | 45 | 4 | 22 | 24 | ||
| 5 | 20 | 50 | 5 | 20 | 60 | ||
| 6 | 12 | 68 | 6 | 20 | 22 | ||
| 7 | 5 | 20 | 7 | 9 | 36 | ||
| 8 | 3 | 50 | 8 | 8 | 42 | ||
| 9 | 12 | 48 | 9 | 15 | 35 | ||
| 2 | 0 | 10 | 30 | 3 | 0 | 5 | 40 |
| 1 | 20 | 80 | 1 | 6 | 36 | ||
| 2 | 15 | 45 | 2 | 7 | 35 | ||
| 3 | 12 | 38 | 3 | 12 | 24 | ||
| 4 | 14 | 18 | 4 | 15 | 15 | ||
| 5 | 8 | 42 | 5 | 12 | 32 | ||
| 6 | 10 | 45 | 6 | 9 | 42 | ||
| 7 | 18 | 22 | 7 | 10 | 45 | ||
| 8 | 25 | 40 | 8 | 7 | 21 | ||
| 9 | 5 | 42 | 9 | 20 | 36 | ||
| 4 | 0 | 5 | 18 | 5 | 0 | 20 | 45 |
| 1 | 10 | 18 | 1 | 19 | 38 | ||
| 2 | 12 | 30 | 2 | 21 | 15 | ||
| 3 | 24 | 30 | 3 | 18 | 26 | ||
| 4 | 6 | 24 | 4 | 15 | 18 | ||
| 5 | 12 | 52 | 5 | 16 | 50 | ||
| 6 | 3 | 15 | 6 | 8 | 30 | ||
| 7 | 15 | 45 | 7 | 7 | 20 | ||
| 8 | 19 | 50 | 8 | 10 | 24 | ||
| 9 | 20 | 25 | 9 | 13 | 48 |
| № задачи | вариант | Р, кВт | w, рад/с | № задачи | вариант | Р, кВт | w, рад/с |
| 6 | 0 | 4 | 35 | 7 | 0 | 16 | 40 |
| 1 | 20 | 15 | 1 | 30 | 50 | ||
| 2 | 18 | 20 | 2 | 28 | 42 | ||
| 3 | 16 | 18 | 3 | 20 | 38 | ||
| 4 | 30 | 24 | 4 | 15 | 20 | ||
| 5 | 25 | 30 | 5 | 18 | 30 | ||
| 6 | 22 | 28 | 6 | 22 | 30 | ||
| 7 | 15 | 18 | 7 | 27 | 35 | ||
| 8 | 8 | 24 | 8 | 24 | 28 | ||
| 9 | 10 | 12 | 9 | 4 | 20 | ||
| 8 | 0 | 12 | 38 | 9 | 0 | 40 | 70 |
| 1 | 15 | 42 | 1 | 30 | 50 | ||
| 2 | 10 | 32 | 2 | 32 | 38 | ||
| 3 | 20 | 50 | 3 | 25 | 42 | ||
| 4 | 23 | 18 | 4 | 12 | 32 | ||
| 5 | 14 | 24 | 5 | 28 | 34 | ||
| 6 | 16 | 20 | 6 | 20 | 35 | ||
| 7 | 24 | 15 | 7 | 10 | 20 | ||
| 8 | 26 | 25 | 8 | 14 | 30 | ||
| 9 | 6 | 48 | 9 | 35 | 40 |
