Расчет выходной реакции линейной цепи с помощью операционного метода и метода прямой свертки
СОДЕРЖАНИЕ: Курсовая работа По дисциплине «Радиотехнические цепи и сигналы» Тема: Расчет выходной реакции линейной цепи с помощью операционного метода и метода прямой свертки.Курсовая работа
По дисциплине «Радиотехнические цепи и сигналы»
Тема: Расчет выходной реакции линейной цепи с помощью операционного метода и метода прямой свертки.
Введение
Цель работы:
-Изучить физические процессы в линейных цепях в переходном и установившемся режимах;
-Приобрести навыки применения основных методов анализа преобразования сигналов линейными цепями;
-Приобрести навыки применения дискретного преобразования Фурье (ДПФ) и алгоритма быстрого преобразования Фурье (БПФ) в инженерных расчетах.
Решаемая задача: для заданной цепи и входному сигналу рассчитать выходную реакцию линейной цепи с помощью операционного метода и метода прямой свертки.
Исходные данные. Задание №21, вариант схемы №21.
| № п/п | Сигнал | Параметры сигнала | ||
| U1, В | U2, В | Tu, мкс | ||
| 1 | 3 | 8 | 8 | 16,5 |
| № п/п | Схема цепи | Параметры цепи | |
| R, Ом | C, мкФ | ||
| 1 | 3 | 175 | 0,085 |
Исходный сигнал №21
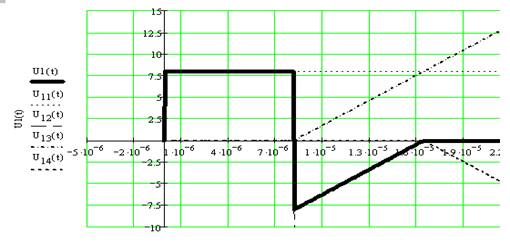
Заданная схема №: 21
Расчет выходного сигнала операционным методом
Аналитическое выражение для заданного входного сигнала его «изображение» по Лапласу.
;
;
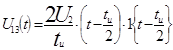
Итоговое уравнение имеет вид:
Используя таблицу преобразований Лапласа, свойство линейности
и теорему запаздывания 
находим:
,
где
;
;
;
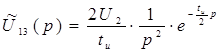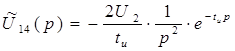
Передаточную функцию цепи находим через операционные сопротивления (проводимости) ветвей по формуле
,
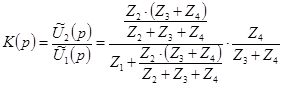где 
- операционное сопротивление i – ой ветви.
Получаем
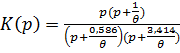, где =RC
Изображение выходного сигнала 
находим как произведение входного сигнала на передаточную функцию цепи:
;
где
, 
.
,
,
.
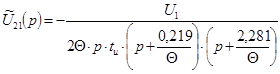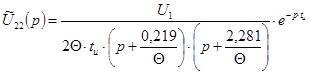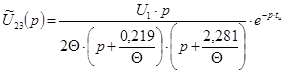Аналитическое выражение выходного сигнала находим как сумму сигналов
,
где:
,
,
.
.
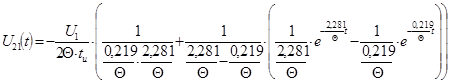
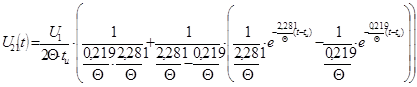
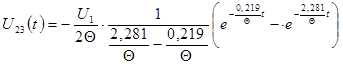Выходной сигнал будет иметь вид:
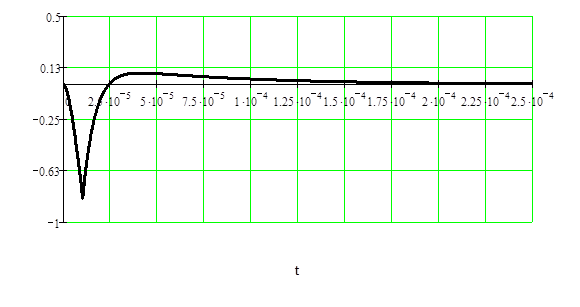
Найдем переходную характеристику линейной цепи и построим ее график. Переходная характеристика равна:
.
Получим
;
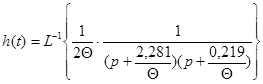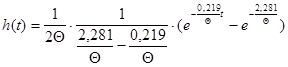
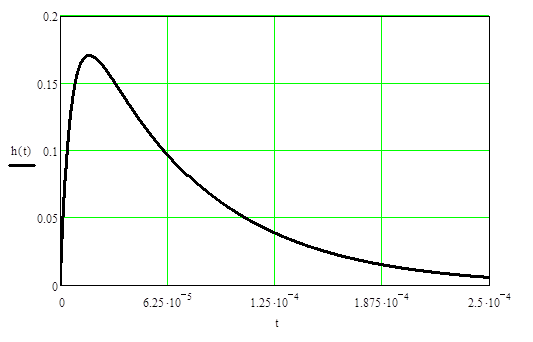
Затем найдем импульсную характеристику линейной цепи и построим ее график. Импульсная характеристика равна:
.
Получим:
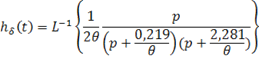
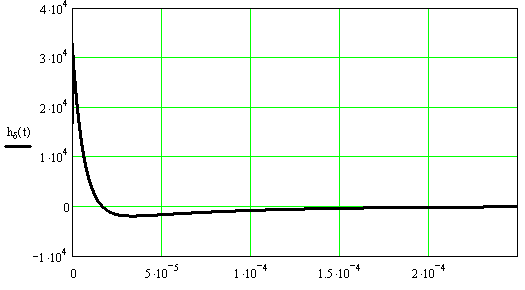
Найдем комплексную частотную характеристику (КЧХ) линейной цепи. Она находится по известной передаточной функции 
формальной заменой переменных 
.
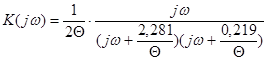
Выражение для АЧХ
, построим ее график:
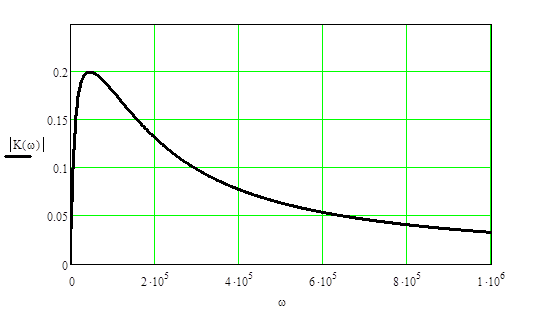
Расчет выходного сигнала методом прямой свертки.
Возьмем количество отсчетов 
и определим период дескритизации по формуле:
Продискретизируем входной сигнал с периодом Т, получится:
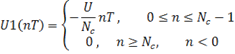
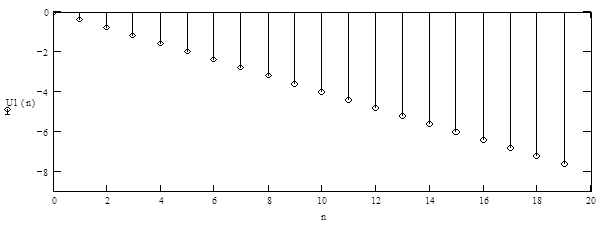
С таким же периодом дескретизации продискретизируем импульсную характеристику 
, т.к. она бесконечна, мы ее обрезаем на уровне 0,05max и после этого дискретизируем. Количество отсчетов определим по формуле:
.
Получится:
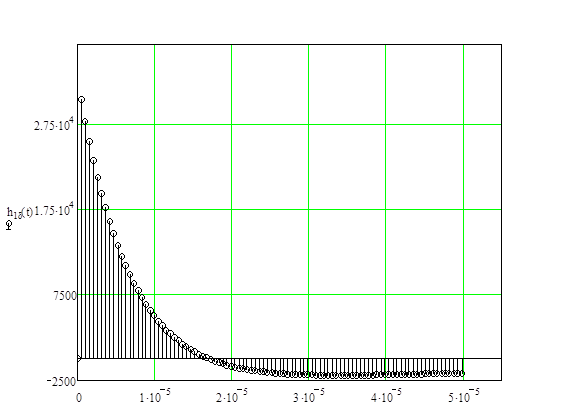
В результате выходной сигнал будет иметь следующий вид:
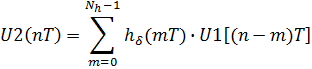
где m – количество отсчетов при дискретизации импульсной характеристики, а n=0,1,2,3….
.
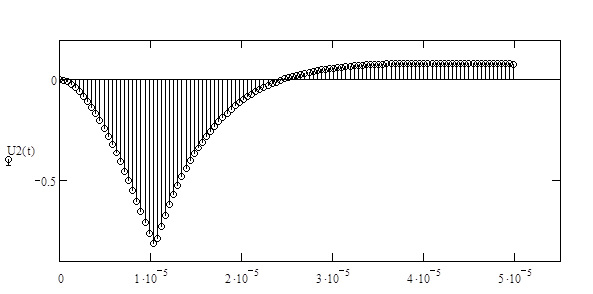
Вывод
1.Операционный метод обладает большой точностью, так как при его использовании выходной сигнал представлен в виде непрерывной функции времени.
2. В методе прямой свертки точность определяется количеством взятых отсчётов. Этим и объясняются различия графиков выходного сигнала рассчитанного разными методами.
3. Ввиду переходных процессов происходит искажение сигнала при прохождении его через цепь, эти искажения определяются топологией и параметрами цепи.
Литература
1. Филончиков В.Д., Карпов О.А. Радиотехнические цепи и сигналы. Методические указания к домашним заданиям и курсовой работе.-М.: ВВИА им. Н.Е. Жуковского,1989.
2. Толстов Е.Ф., Филончиков В.Д.,Школьный Л.А. Радиотехнические цепи и сигналы. Теория сигналов, линейных цепей и систем.-М.:ВВИА им. Н.Е. Жуковского, 1993.