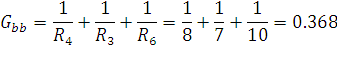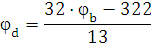Расчёт электрических цепей
СОДЕРЖАНИЕ: ЗАДАНИЕ № 1 ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА В соответствии с вариантом, заданным двумя последними цифрами шифра, указанного в зачетной книжке, выписать из табл. 1.1 и 1.2 условия задачи и выполнить следующее:ЗАДАНИЕ № 1
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
В соответствии с вариантом, заданным двумя последними цифрами шифра, указанного в зачетной книжке, выписать из табл. 1.1 и 1.2 условия задачи и выполнить следующее:
1. Начертить схему электрической цепи с обозначением узлов и элементов ветвей, соблюдая требования ЕСКД.
2. Определить и составить необходимое число уравнений по законам Кирхгофа для определения токов во всех ветвях.
3. Определить токи ветвей методом контурных токов и узловых потенциалов и свести их в таблицу.
4. Проверить результаты расчетов по уравнениям баланса мощностей.
5. Определить ток в первой ветви методом эквивалентного генератора.
Таблица 1.1
| Сопротивления резисторов, Ом. Э.д.с. источников в В и тока в А |
|||||||||||
| R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
Е1 |
E2 |
Е3 |
Е4 |
E5 |
J6 |
| 5 |
6 |
7 |
8 |
9 |
10 |
21 |
22 |
23 |
24 |
25 |
1 |
УСЛОВИЯ К ЗАДАНИЮ № 1.
Таблица 1.2
ЛОГИЧЕСКОЕ СОДЕРЖАНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
| Схема электрической цепи |
| a(R1 +R3 3 bR4 )cR2 2 d(R6 6 b+R5 )а |
РЕШЕНИЕ:
Электрическая схема:
Дано:![]() = 5 Om;
= 5 Om; ![]() = 6 Om;
= 6 Om; ![]() = 7 Om;
= 7 Om; ![]() = 8 Om;
= 8 Om;
![]() = 9 Om;
= 9 Om; ![]() = 10 Om;
= 10 Om;
E2= 22 B; E3 = 23B; J =1A.
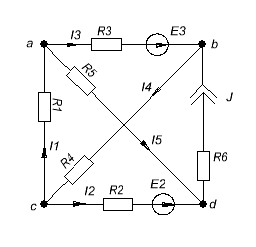
Для нахождения количества контуров упростим схему:
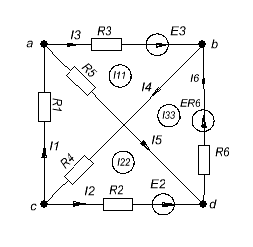
Подставим вместо источника J эдс ER6= 1А·![]()
Определим количество узлов и контуров.
Узлов = 4;
Контуров =4.
Составим необходимое количество уравнений по законам Кирхгофа.
По первому закону n = У -1 =3;
По второму n = К =3.
Общее количество уравнений N = 3+5=8.
По первому закону Кирхгофа:
Узел с: ![]()
Узел а: ![]()
Узел b: ![]()
По второму закону Кирхгофа.
Для контура 1:
![]()
Для контура 2 :
![]()
Для контура 3:
![]()
Подставим числовые значения:
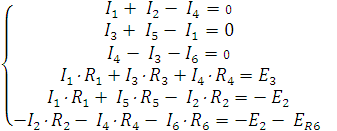
Рассчитаем токи методом контурных токов(МКТ).
В данной схеме 3 независимых контура. Значит и уравнений будет тоже 2.
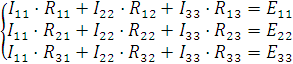 , где
, где
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Подставим полученные значения в систему уравнений:
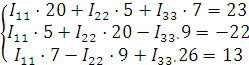
Решим уравнения и найдем контурные токи.
Выразим  из первого уравнения через
из первого уравнения через  , из третьего
, из третьего  через
через  и подставим во второе.
и подставим во второе.
![]()
Подставим это выражение в уравнение 2,3
Составим новую систему уравнений
![]()
Выразим из первого уравнений ![]() через
через ![]()
![]()
Подставим во второе уравнение
![]()
![]()
Найдем ![]() ,
, ![]()
![]()
![]()
Далее выразим истинные токи через контурные токи:
![]()
![]()
![]()
![]()
![]()
![]()
Определим баланс мощности
![]() . = 72.953 Вт.
. = 72.953 Вт.
![]() = 73.29.
= 73.29.
Допускается расхождение
![]()
Баланс сходится , значит расчет верен.
Определим токи во всех ветвях методом узловых потенциалов.
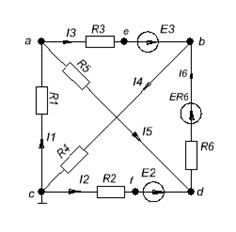
Выберем в качестве нулевого узла узел «с». Необходимо найти потенциалы узлов a,b,d.
Вычислим собственные проводимости этих узлов:
![]() =
=![]()
Общая проводимость этих узлов:
![]()
![]()
![]()
Находим узловые токи:
В узле «а»:
![]()
![]()
![]()
Составим систему уравнений для нахождения потенциалов узлов по методу узловых потенциалов.
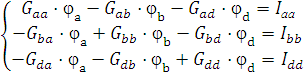
Подставляем числовые значения
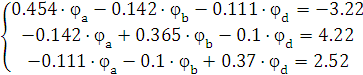
Решим эту систему и найдем потенциалы узлов. Выразим  из первого уравнения через
из первого уравнения через  .
.
Подставим полученный результата во второе уравнение.
=-3.22 + 0.322· - 0.133·
- 0.133·
Подставим в третье уравнение.
=-1.734 – 0.134 + 0.344·
+ 0.344·
Запишем новую систему.
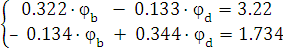
Выразим из первого уравнения ![]() через
через ![]()
Подставим во второе уравнение
70.7· =1015
=1015
 =14.36 В
=14.36 В
Найдем ![]() =
=![]() =10.58 В.
=10.58 В.
Найдем  = - 0.17 В.
= - 0.17 В.
Рассчитаем токи
![]()
![]()
![]()
![]()
![]()
Как видно, токи, полученные методом контурных токов и методом узловых потенциалов примерно равны. Погрешности объясняются округлением результатов вычислений.
Определение тока методом эквивалентного генератора.
Найдем ток  .
.
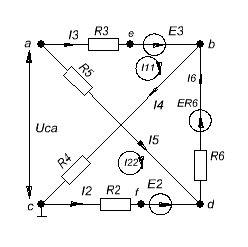
Определим токи в ветвях этой схемы методом контурных токов.
![]()
Найдем  и
и  и выразим через них истинные токи в ветвях этой схеме.
и выразим через них истинные токи в ветвях этой схеме.
![]()
![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
Внутреннее сопротивление эквивалентного источника равно входному сопротивлению относительно выводов « ac» пассивного двухполюсника.

![]()
Преобразуем схему
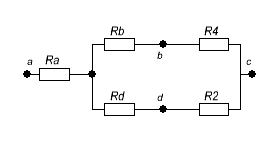
![]()
![]()
![]()
Тогда
![]()
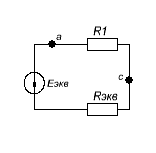
Окончательная схема имеет вид
По закону Ома:
![]()
ЗАДАНИЕ № 2
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО
СИНУСОИДАЛЬНОГО ТОКА
Выписать из табл. 2.1 и 2.2 условия задания и выполнить следующее.
1. Начертить схему электрической цепи, соблюдая требования ЕСКД.
2. Составить уравнения по законам Кирхгофа для токов в интегро-дифференциальной и символической формах.
3. Применить один из методов расчета линейных электрических цепей. Определить комплексные действующие токи во всех ветвях цепи. Записать выражения для мгновенных значений токов. Частота тока во всех вариантах
4. = 400 Гц.
5. Построить топографическую диаграмму для цепи, совмещенную с векторной диаграммой токов.
6. Обозначить произвольно начала двух катушек в любых двух ветвях и предусмотрев взаимную индуктивную связь М между ними, записать уравнения, составленные по законам Кирхгофа в интегро-дифференциальной и в символической формах.
7. Определить показания ваттметра цепи.
P=Re
![]()
УСЛОВИЯ К ЗАДАНИЮ №2.
Таблица 2.1
ЗНАЧЕНИЯ ПАРАМЕТРОВ ЦЕПИ
| L1 L2 L3 мгн |
С1 С2 С3 мкф |
R1 R2 R3 Ом |
Й1 Еs 2 Й2 Еs 2 Й3 ES 3 В/град |
г, Гц |
|||||||||||
| 7 |
8 |
7 |
5 |
4 |
5 |
2 |
0 |
8 |
14/45 |
20/0 |
10/60 |
50/30 |
50/0 |
18/90 |
400 |
Таблица 2.2
ЛОГИЧЕСКОЕ СОДЕРЖАНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
| Схема электрической цепи |
| a(1 R1 L1 +2 C2 +3 L3 R3 C3 )b |
РЕШЕНИЕ:
Исходные данные
![]() = 2 Ом;
= 2 Ом; ![]() ;
;
![]() =0,007 Гн;
=0,007 Гн; ![]() =0,007 Гн;
=0,007 Гн;
![]() =4 мкФ;
=4 мкФ; ![]() =5 мкФ;
=5 мкФ;
![]() ;
; ![]() ;
;![]() .
.
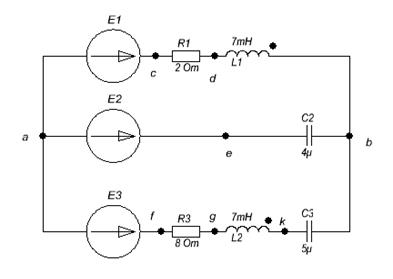
Составим уравнения по законам Кирхгофа в интегро-дифференциальной и символической формах. Направление токов выберем произвольно.
Перейдем от мгновенных значений ЭДС к комплексам действующих значений.
![]()
![]()
![]()
=2рf=23.14400=2513.27 рад/с
![]()
![]()
![]()
Интегро-дифференциальная форма.
![]()
![]()
![]()
![]()
Комплексная форма.
![]()
![]()
![]()
![]()
Где
![]() =2+j17.59=17.7
=2+j17.59=17.7![]()
![]() = - j99.47=99.47
= - j99.47=99.47![]()
![]() =8 – j61.98=62.5
=8 – j61.98=62.5![]()
3. Определим комплексные действующие токи во всех цепях.
Применим метод узловых потенциалов. Найдем проводимости цепей.
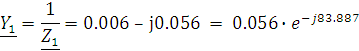
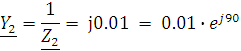

Пусть ![]() , тогда по методу двух узлов(частный случай метода узловых потенциалов) имеем:
, тогда по методу двух узлов(частный случай метода узловых потенциалов) имеем:
![]()
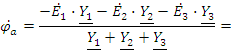
![]()
![]() .
.
Теперь рассчитаем токи.
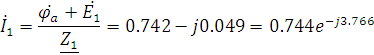
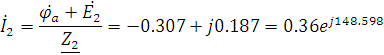
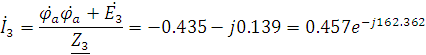
Проверим уравнения, составленные по законам Кирхгофа.
1) ![]()
2) ![]()
![]() (
(![]() )( - j99.47)=-16.47-J17.675
)( - j99.47)=-16.47-J17.675
![]()
3) ![]()
(![]()
![]()
![]()
4) ![]()
![]()
![]()
![]()
Как видно, все уравнения сошлись.
4. Векторная диаграмма, совмещенная с топографической.
Найдем потенциалы остальных точек.
1) ![]()
![]()
![]()
![]()
2) ![]()
![]()
3) ![]()
![]()
![]()
Небольшие неточности в неравнозначности ![]() связаны с погрешностями расчетов.
связаны с погрешностями расчетов.
Построим диаграмму.
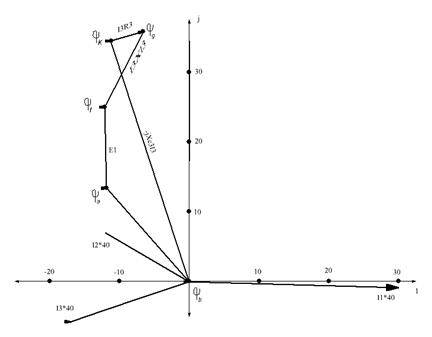
5. Взаимоиндукция.
Обозначим начала катушек и запишем уравнения, составленные по законам Кирхгофа. M – взаимоиндукция.
1) ![]()
2) ![]()
3) 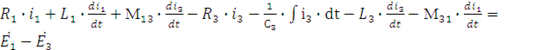
В символической форме:
1) ![]()
2) ![]()
3) ![]()
6. Определить показание ваттметра.
P=Re[![]() =
=![]()
P=U·I·![]() =
=![]() =8.178 Вт.
=8.178 Вт.
ЗАДАНИЕ № 3
ПЕРЕХОДНЫЕ ПРОЦЕССЫ
Выписать из табл. 3.1 и 3.2 условия задания и выполнить следующее:
1. Начертить схему электрической цепи с обозначением узлов и элементов ветвей.
2. Рассчитать переходный процесс классическим и операторным методами: т.е. определить для тока в одной из ветвей и для напряжения на одном из элементов ветвей в функции времени.
3. Построить графики переходных процессов в функции времени.
4. Определить энергию, рассеиваемую на одном из резисторов цепи в переходном процессе.
Примечание: символу « K » соответствует разомкнутое состояние ключа до коммутации.
Таблица 3.1
ЗНАЧЕНИЯ ПАРАМЕТРОВ ЦЕПИ
| R1 Ом |
R2 Ом |
R3 Ом |
L1 мгн |
C1 мкф |
L2 мгн |
C2 мкф |
Е В |
| 10 |
2 |
40 |
100 |
10 |
10 |
5 |
12 |
Таблица 3.2
ЛОГИЧЕСКОЕ СОДЕРЖАНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
| Схема электрической цепи |
| a(L1 R1 +ER3 +KC1 )b |
РЕШЕНИЕ:
Исходные данные:
R1 =10 Ом; R3=40 Ом ;
E1=12 В; С=10мкФ;
L=100 мГн.
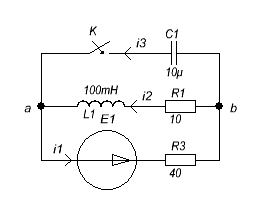
1. Расчет классическим методом.
1) Расчет режима до коммутации (при t = 0_ )
i1
(0_) = i2
(0_)=![]()
i3 (0_)=0
uc (0+ )= 0
по независимым начальным условиям( законам коммутации):
i2
(0+
)= i2
(0_)=![]()
uc (0+ )=uc (0_)=0
2) Составим характеристическое уравнение
Z(p)=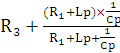 =
=![]()
![]()
Подставляем числовые значения:
40·10-5
·0.1·p2
+(40·10·10-5
·+0.1)p+50=0![]()
4·10-5 ·p2 +0.104·p+50=0
Найдем корни уравнения:
P1,2=![]()
P1![]() -636.675c-1
-636.675c-1
P2![]() -1963.325c-1
-1963.325c-1
Корни действительные и разные, значит переходной процесс будет апериодическим.
3) Запишем свободную составляющую тока i2
i2
св
(t)=A1
·![]() +A·
+A·![]() ,
,
где А1, А2 – постоянные интегрирования.
![]()
![]() , поэтому экспонента с показателем p2
t будет заухать быстрее, чем с показателем p1
t.
, поэтому экспонента с показателем p2
t будет заухать быстрее, чем с показателем p1
t.
4) Расчет установившегося режима после коммутации.
i2
пр = i1
пр=![]()
i3 пр =0
uc
пр
= i2
пр
·![]() 2.4В
2.4В
5) Свободные составляющие токов напряжений при t=0+ найдем как разницу между переходными и принужденными величинами.
i2 св (0+ )= i2 (0+ ) - i2 пр = 0.24-0.24=0
uc св (0+ )= uc (0+ )- uc пр =0-2.4=-2.4В
по второму закону Кирхгофа для свободны составляющих:
L![]()
![]() =
=![]()
6) Определим постоянные интегрирования по начальным условиям
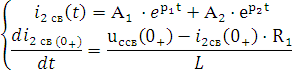
Подставим в эти уравнения при ![]()
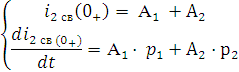
![]()
Из первого уравнения имеем А1 =-А2
Подставим это выражение во второе и получим А2
-![]() ·p1
+
·p1
+![]()
![]()
![]() A
A
![]() A
A
7) Ток i2 (t) найдем как сумму его принужденной и свободной составляющих.
![]() (t)=
(t)=![]() +
+ ![]() =
=![]() A1
·
A1
·![]() +A2
·
+A2
·![]() =0.24 -0.0180912·
=0.24 -0.0180912·![]() , А
, А
Для проверки подставим в это уравнение ![]() , получим
, получим ![]() (
(![]() )=0.24А, что совпадает с расчетом по п.1.
)=0.24А, что совпадает с расчетом по п.1.
2. Расчет операторным методом.
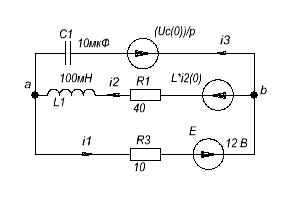
Определим ![]()
Расчет режима до коммутации:
![]()
![]()
![]()
1) Начальные условия:
![]()
![]()
2) Составим систему уравнений по 1 и 2 законам Кирхгофа.
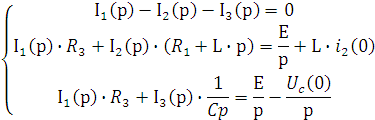
Выразим из 2 уравнения ![]() , из 3 -
, из 3 - ![]() и подставим в первое.
и подставим в первое.
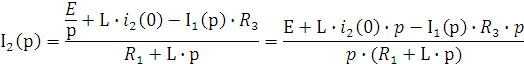
![]()
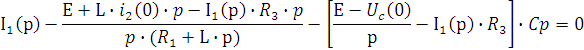
![]()
Т.к. ![]() , то
, то
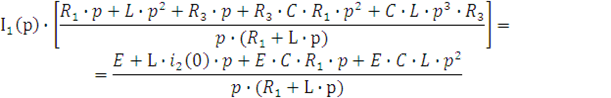
![]()
Подставим числовые значения.
![]()
Найдем корни уравнения ![]() .
.
![]()
![]()
![]()
![]()
![]()
Корни действительные и разные. Значит, переходной процесс будет апериодическим.
3) Для перехода от изображения к оригиналу воспользуемся формулой разложения для простых корней.
![]()
В соответствии с этой формулой ток ![]() будет равен:
будет равен:
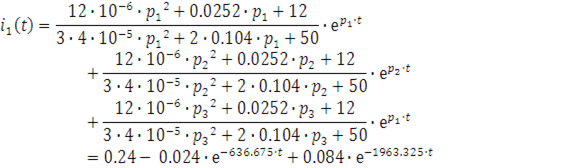
Напряжение ![]()
4) Определим энергию, рассеивающуюся на ![]() при переходном процессе. Переходной процесс заканчивается примерно при T=4t, где t – наименьший по модулю корень характеристического уравнения.
при переходном процессе. Переходной процесс заканчивается примерно при T=4t, где t – наименьший по модулю корень характеристического уравнения.
![]()
![]()
![]()
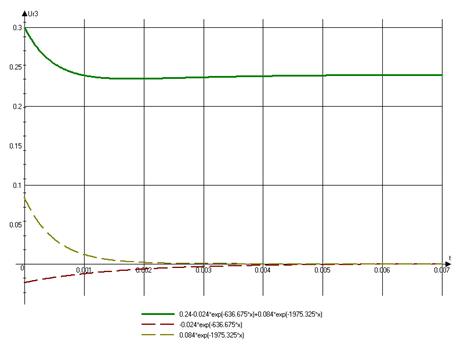
5) Построим графики переходных процессов.
Для тока ![]()
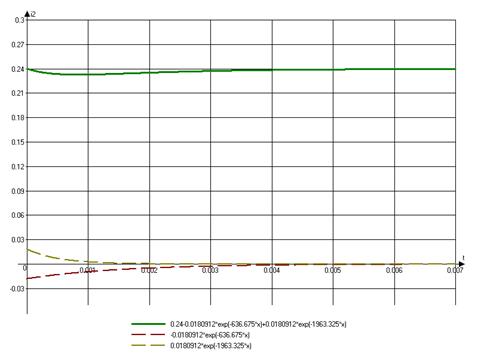
Для ![]()