Разработка алгоритма программы нахождения производной методом неопределённых коэффициентов

СОДЕРЖАНИЕ: ТУЛЬСКИЙ АРТИЛЛЕРИЙСКИЙ ИНЖЕНЕРНЫЙ ИНСТИТУТ Кафедра №10 «Математического, программного и информационного обеспечения АСУ» ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

ТУЛЬСКИЙ АРТИЛЛЕРИЙСКИЙ ИНЖЕНЕРНЫЙ ИНСТИТУТ

Кафедра №10 «Математического, программного и

информационного обеспечения АСУ»

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовому проекту по дисциплине

«1001 – Дискретная математика»

Тема: «Разработка алгоритма программы нахождения производной

м етодом неопределённых коэффициентов»

Руководитель:

Исполнитель:

СОДЕРЖАНИЕ

Введение

1.Постановка и уяснение задачи:

1.1Анализ предметной области

1.1.1 Метод неопределённых коэффициентов

1.1.2 Использование интерполяционных многочленов

1.1.3 Использование конечно разностных соотношений для аппроксимации производных

2. Разработка алгоритма и программы:

2.1 Разработка алгоритма

2.2 Обоснование выбора языка программирования

2.3 Разработка программы

3.Экспериментальное исследование алгоритма и программы:

3.1Решение задачи методом неопределённых коэффициентов

3.2 Тестирование программы

3.3. Руководство программисту

Заключение

Список литературы

Приложение А

Приложение Б

В ведение

Задача решения обыкновенных дифференциальных уравнений сложнее задачи вычисления однократных интегралов, и доля задач, интегрируемых в явном виде, здесь существенно меньше.

Когда говорят об интегрируемости в явном виде, имеют в виду, что решение может быть вычислено при помощи конечного числа “элементарных” операций: сложения, умножения, вычитания, деления, возведения в степень, логарифмирования, потенцирования, вычисление синуса и косинуса и т.д.

Уже в период, предшествовавший появлению ЭВМ, понятия “элементарной” операции претерпели изменения. Решение некоторых частных задач настолько часто встречаются в приложениях, что пришлось составить таблицы их значений, в частности таблицы интегралов Френеля, функций Бесселя и ряда других так называемых специальных функций. При наличии таких таблиц исчезает принципиальная разница между вычислением функций sinx, lnx,… и специальных функций. В том и другом случаях можно вычислять значения этих функций при помощи таблицы, и те и другие функции можно приближая их многочленами, рациональными дробями и т.д.

Таким образом, в класс задач, интегрируемых в явном виде, включились задачи, решение которых выражаются через специальные функции. Однако и этот, более широкий, класс составляет относительно малую долю задач, предъявляемых к решению. Существенное расширение класса реально решаемых дифференциальных уравнений, а следовательно и расширение сферы применения математики произошло с разработкой численных методов и активным повсеместным использованием ЭВМ.

В настоящее время затраты человеческого труда при решении на ЭВМ задачи Коши для обыкновенных дифференциальных уравнений сравнимы с затратами на то, чтобы просто переписать заново формулировку этой задачи.

При желании можно получить график решения или его изображение на экране. В результате этого для многих категорий научных работников существенно уменьшился интерес к изучению частных способов интегрирования обыкновенных дифференциальных уравнений в явном виде.

Эта работа посвящена описанию одного из методов решения задачи Коши для обыкновенных дифференциальных уравнений и исследования свойств этого метода.

Обратим внимание на то обстоятельство, что как и в других случаях, первоначальный анализ практической пригодности метода производится, изучая простейшие задачи, где точное и приближенное решение задачи выписываются в явном виде.

1.Постановка и уяснение задачи

Необходимо разработать алгоритм и программу, выполняющую задачу по нахождению производной методом неопределённых коэффициентов. Необходимо провести анализ существующих методов решения поставленной задачи. Наиболее подходящим считать метод неопределённых коэффициентов. Результатом выполнения работы иметь корректно работающую программу и правильно оформленную техническую документацию.

1.1 Анализ предметной области

1.1.1 Метод неопределённых коэффициентов

Метод неопределённых коэффициентов применяется для численного дифференцирования таблично заданной функции с произвольным расположением узлов. Он заключается в следующем.

Искомое выражение для производной k -го порядка для некоторой точке x = x_i представляется в виде линейной комбинации заданных значений функции в узлах x ₀ , x ₁ , …, x_n :

y_i ^(k) =C₀ y₀ +C₁ y₁ +…+C_n y_n . (2.1)

Предполагается, что эта формула имеет место для многочленов:

y=1; y=x-x_i ;…; y=(x-x_i )ⁿ .

Подставляя последовательно эти многочлены в выражение (2.1) можно получить систему линейных алгебраических уравнений для определения коэффициентов С₀ , С₁ , …, С _{n .}

Рассмотрим порядок использования данного метода для нахождения производной на следующем примере.

Пример. Найти выражение для определения производной у₁ в случае задания функции в четырёх равноотстоящих узлах.

Решение. Равенство (2.1) запишется в следующем виде

y_i ^{( k )} = C ₀ y ₀ + C ₁ y ₁ +С₂ у₂ + C ₃ у₃ . (2.2)

Для нахождения производной у₁ используем, например, следующие многочлены:

y =1; y = x - x ₀ ; у=(х-х₀ )² ; y =( x - x ₀ )³ . . (2.3)

Производные этих многочленов будут иметь следующий вид соответственно:

y =0; y =1; у=2(х-х₀ ); y =3( x - x ₀ )² . . (2.4)

Подставляя последовательно соотношения (2.3) и (2.4) соответственно в правую и левую части равенства (2.2), получим в общем виде при х=х₁ , следующую систему линейных алгебраических уравнений для определения коэффициентов С₀ , С₁ , …, С _n :

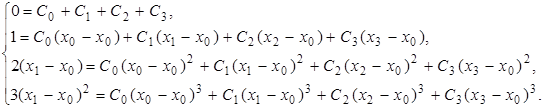
После упрощения данная система линейных алгебраических уравнений примет следующий вид:

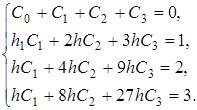
Решив данную систему уравнений, получим следующие значения коэффициентов и выражение для нахождения производной у₁ :

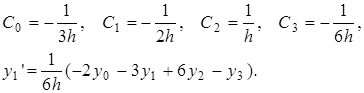
1.1.2 Использование интерполяционных многочленов

Пусть функция f(x) задана в виде таблицы y_i = f (x_i ) , i=0,1,…n с постоянным шагом h . Предположим, что эта функция может быть аппроксимирована интерполяционным многочленом Ньютона:

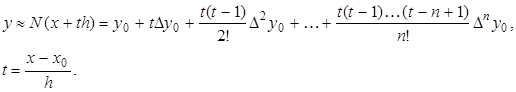
Этот многочлен можно продифференцировать по х с учётом правила дифференцирования сложной функции:

В результате можно получить формулы для вычисления производных любого порядка. Например:

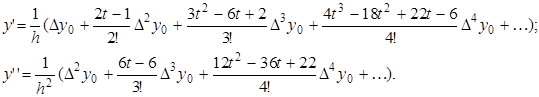
Пусть та же функция может быть аппроксимирована интерполяционным многочленом Лагранжа. Рассмотрим интерполяционный многочлен Лагранжа для случая трёх узлов интерполяции (n=2):

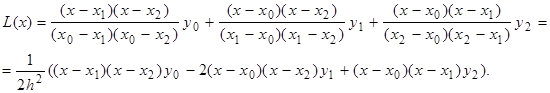
Этот многочлен можно продифференцировать по х , тогда первая производная будет иметь следующий вид:

В частности,

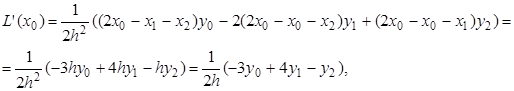
1.1.3 Использование конечно разностных соотношений для аппроксимации производных

Производной функции y = f ( x ) в точке x ₀ называется предел при D x ® 0 отношения приращения функции в этой точке к приращению аргумента (при условии, что этот предел существует). Для обозначения производной функции y=f(x) в точке x₀ используют символы y ( x ₀ ) или f ( x ₀ ) . То есть, по определению,

(1.1)

Аппроксимацией (приближением) производной с помощью отношения конечных разностей называется соотношение (1.2) в котором значения D у , D х конечные, в отличие от их бесконечно малых значений в (1.1).

(1.2)

Пусть функция задана таблично с постоянным шагом h .

x0	x1	x2	…	xn
y0	y1	y2	…	yn

В зависимости от способа вычисления конечных разностей можно получить разные формулы для вычисления производных в одной и той же точке. Например, для нахождения производной y ₁ можно использовать формулы левых, правых и центральных разностей, которые имеют следующий вид соответственно:

D y₁ =y₁ - y₀ , D x=h, y₁ =(y₁ - y₀ )/h;

D y₁ =y₂ - y₁ , D x=h, y₁ =(y₂ - y₁ )/h;

D y₁ =y₂ - y₀ , D x=2h, y₁ =(y₂ - y₀ )/2h.

Аналогично можно найти выражения для определения старших производных. Например:

y ₁ =( y ₁ )=( y ₂ - y ₁ )/ h =(( y ₂ - y ₁ )/ h - ( y ₁ - y ₀ )/ h ) h =( y ₂ - 2 y ₁ + y ₀ )/ h ² .

Оценим погрешность численного дифференцирования с помощью рассмотренных конечно-разностных соотношений. Для этого аппроксимируем функцию f ( x ) некоторой функцией j ( x ) , т.е. представим её в виде

f ( x )= j ( x )+ R ( x ). (1.3)

В качестве j ( x ) можно принять частичную сумму ряда или интерполяционную формулу. Тогда погрешность аппроксимации R ( x ) определяется остаточным членом ряда или интерполяционной формулы. Аппроксимирующая функция j ( x ) может быть использована для приближённого вычисления производной. Дифференцируя равенство (1.3) необходимое количество раз, можно найти значение производной f ^{( l )} ( x )= j ^{( l )} ( x )+ R ^{( l )} ( x ) . Величина R ^{( l )} ( x )= f ^{( l )} ( x ) - j ^{( l )} ( x ) называется погрешностью аппроксимации производной.

При численном дифференцировании функции, заданной в виде таблицы с шагом h , эта погрешность зависит от h и её записывают в виде O ( h^k ). Показатель степени k называют порядком погрешности аппроксимации производной. При этом предполагается, что | h | 1 .

Оценку погрешности легко проиллюстрировать с помощью ряда Тейлора:

Пусть функция f ( x ) задана в виде таблицы f ( x_i )= y_i , i =0,1,… n . Запишем разложение этой функции в ряд Тейлора при x = x ₁ , D x = - h с точностью до членов ряда порядка h :

y ₀ = y ₁ - y ₁ h + O ( h ² ).

Отсюда можно найти значение производной в точке x = x ₁ :

y₁ = (y₁ - y₀ )/h + O(h² )/h = (y₁ - y₀ )/h + O(h).

Эта формула совпадает с формулой нахождения производной с помощью левых разностей и имеет первый порядок точности.

Аналогично, при x = x ₁ , D x = h получается выражение для нахождения производной с помощью правых разностей, которая также имеет первый порядок точности:

y ₁ = ( y ₂ - y ₁ )/ h + O ( h ).

Используем теперь ряд Тейлора для оценки погрешности аппроксимации производной с помощью центральных разностей. Полагая D x = - h и D x = h при x = x ₁ , можно получить:

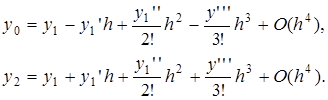
Вычитая первое равенство из второго, получаем

Откуда можно получить выражение для нахождения производной с помощью правых разностей, которая имеет второй порядок точности:

y ₁ = ( y ₂ - y ₀ )/2 h + O ( h ² ).

Складывая оба равенства, можно оценить погрешность аппроксимации производной второго порядка:

y₁ = (y₂ - 2y₁ +y₀ )/h² + O(h² ).

Эта аппроксимация имеет также второй порядок точности.

Вывод

Существует много способов решения данной проблемы, а именно нахождения производной. Все они имеют свои преимущества и недостатки. Говоря о достоинствах рассматриваемого нами метода (неопределённых коэффициентов), можно сказать о:

1.Его точности

2.Простом способе применения

3.Его распространённости

2. Разработка алгоритма и программы

2.1 Разработка алгоритма

Алгоритм метода наименьших квадратов включает следующие шаги:

1. Пояснение к программе и ввод данных.

2. Организуется цикл для расчёта коэффициентов при наличии в уравнении x-a5-ой степени.

3. Организуется цикл для расчёта коэффициентов при наличии в уравнении x-a4-ой степени.

4. Организуется цикл для расчёта коэффициентов при наличии в уравнении x-a3-ой степени.

5. Организуется цикл для расчёта коэффициентов при наличии в уравнении x-a2-ой степени.

6. Вывод полученного уравнения и неопределённых коэффициентов на экран.

2.2 Обоснование выбора языка программирования

Прогресс компьютерных технологий определил процесс появления новых разнообразных знаковых систем для записи алгоритмов – языков программирования. Смысл появления такого языка – оснащённый набор вычислительных формул дополнительной информации, превращает данный набор в алгоритм. Язык программирования служит двум связанным между собой целям: он даёт программисту аппарат для задания действий, которые должны быть выполнены, и формирует концепции, которыми пользуется программист, размышляя о том, что делать.

Си ++ - это универсальный язык программирования, задуманный так, чтобы сделать программирование более приятным для серьёзного программиста. За исключением второстепенных деталей Си ++ является надмножеством языка программирования Си. Помимо возможностей, которые дает Си, Си ++ предоставляет гибкие и эффективные средства определения новых типов. Используя определения новых типов, точно отвечающих концепциям приложения, программист может разделять разрабатываемую программу на легко поддающиеся контролю части. Такой метод построения программ часто называют абстракцией данных. Информация о типах содержится в некоторых объектах типов, определённых пользователем. Такие объекты просты и надёжны в использовании в тех ситуациях, когда их тип нельзя установить на стадии компиляции. Программирование с применением таких объектов часто называют объектно-ориентированным. При правильном использовании этот метод даёт более короткие, проще понимаемые и легче контролируемые программы.

Си ++ обеспечивает полный набор операторов структурного программирования. Он также предлагает необычно большой набор операций. Многие операции Си ++ соответствуют машинным командам, и поэтому допускают прямую трансляцию в машинный код. Разнообразие операций позволяет выбирать их различные наборы для минимизации результирующего поля.

Си ++ поддерживает указатели не переменные и функции. Указатель на объект программы соответствует машинному адресу этого объекта. Посредством разумного использования указателей можно создавать эффективно-выполняемые программы, так как указатели позволяют ссылаться на объекты тем же самым путём, как это делает машина. Си ++ поддерживает арифметику указателей, и тем самым позволяет осуществлять непосредственный доступ и манипуляции с адресами памяти.

В своём составе Си ++ содержит препроцессор, который обрабатывает текстовые файлы перед компиляцией. Среди его наиболее полезных приложений при написании программ на Си ++ являются: определение программных констант, замена вызова функций аналогичными, но более быстрыми макросами, условная компиляция. Препроцессор не ограничен процессированием только исходных текстовых файлов Си ++, он может быть использован для любого текстового файла.

Си ++ - гибкий язык, позволяющий принимать в конкретных ситуациях самые разные решения.

2.3 Разработка программы

Основываясь на разработанном алгоритме и выбранном языке, была написана программа.

Тело программы состоит из главной функции, а сама функция из пяти операторов условия (if).

Программа начинается с подключения стандартной библиотеки “iostream”.

Далее в программе при помощи встроенного в язык потока вывода “cout” мы выводим на экран условия выполнения задачи, а так же её условия и примечания, необходимые для правильной и корректной работы программы.

coutProgramma dli naxoshdenui neopredelennux koefficientovendl;

coutRukovodstvo:endl;

coutVvedite koeffichenti pered X, nachinai s naimenshey stepeni X-aendl;

coutPrimechanie:endl;

coutEsli v uravnenie otsutstvuet X c kakoy libo stepenu, ne bolshe 5-oy,endl;

coutto ego koefficent = 0endl;

coutUslovia:endl;

coutMaximalnai stepen X-a ne bolshe 5-oyendl;

coutMaximalnai stepen y-ka ne bolshe 1-oyendl;

coutx0=0 , c0=1endl;

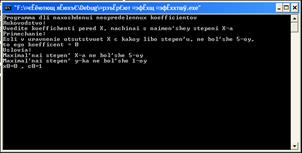
Это поможет даже самому неопытному программисту разобраться в сущности работы программы и научиться ей пользоваться.

Далее вводятся локальные переменные.

doublec1,c2,c3,c4,c5,c6;

double a,c,e,g,j;

cina;

cinc;

cine;

cing;

cinj;

Их роль в программе заключается в том, чтобы составить условие, при котором программа должна выбрать верный путь решения того или иного уравнения. Все эти переменные представляют собой коэффициенты перед переменными “х” различных степеней нашего исходного уравнения. В зависимости от присутствия или не присутствия переменной “x” той или иной степени в уравнении, получаем конкретную степень выходного уравнения.

Далее используем оператор if (оператор условия) для определения в исходном уравнение переменной “х” пятой степени, т.к. это максимальная степень “x”, под которую рассчитана программа.

if(j!=0){

c1=c0;c2=(c1+a)/2;c3=(c2+c)/3;c4=(c3+e)/4;c5=(c4+g)/5;c6=(c5+j)/6;

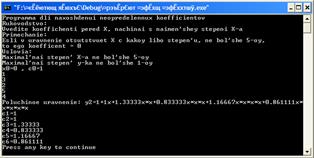
coutPoluchennoe uravnenie:y2=c1+c2x+c3x*x+c4x*x*x+c5x*x*x*x+c6x*x*x*x*xendl;}

Мы видим, что при выполнении данного условия программа выводит на экран полученное уравнение, вместе с подстановкой доселе неизвестных неопределённых коэффициентов в него.

При невыполнение данного условия программа переходит к следующему оператору if и производит те же самые действия, что и с первым оператором. Так продолжается до тех пор, пока в программе не выполнится выше указанное условие.

else if(g!=0){

c1=c0;c2=(c1+a)/2;c3=(c2+c)/3;c4=(c3+e)/4;c5=(c4+g)/5;c5=(c4+g)/5;

coutPoluchennoe uravnenie:y2=c1+c2x+c3x*x+c4x*x*x+c5x*x*x*xendl;}

else if(e!=0){

c1=c0;c2=(c1+a)/2;c3=(c2+c)/3;c4=(c3+e)/4;c5=(c4+g)/5;

coutPoluchennoe uravnenie:y2=c1+c2x+c3x*x+c4x*x*xendl;}

else if(c!=0){

c1=c0;c2=(c1+a)/2;c3=(c2+c)/3;c4=0;c5=0;c6=0;

coutPoluchennoe uravnenie:y2=c1+c2x+c3x*xendl;}

else if(a!=0){

c1=c0;c2=(c1+a)/2;c3=0;c4=0;c5=0;c6=0;

coutPoluchennoe uravnenie:y2=c1+c2xendl;}

При выполнении условия и выводе на экран уравнения, программа выводит на экран отдельно от полученного уравнения неопределённые коэффициенты.

coutc1=c1endlc2=c2endlc3=c3endlc4=c4endlc5=c5endlc6=c6endl;

В случае невыполнения ни одного из пяти условий программа выдаст сообщение об ошибке:

else {coutUravnenie smisla ne imeetendl;}

Выводы:

Произведённые в предыдущих пунктах исследования позволили составить алгоритм поиска значений неопределённых коэффициентов;

1) Обоснован выбор языка программирования;

2) На основе составленного алгоритма составлена программа поиска значений неопределённых коэффициентов.

3) На основе составленного алгоритма составлена программа поиска неопределённых коэффициентов.

3.Экспериментальное исследование алгоритма и программы

3.1 Решение задачи методом неопределённых коэффициентов

Метод неопределённых коэффициентов состоит в том, что решение уравнения ищется в форме ряда с неизвестными коэффициентами:

y = a + b ( x - x ₀ ) + c ( x - x ₀ )² + …,

которые находятся при помощи подстановки в уравнение, последующего приравнивания коэффициентов при одинаковых степенях и применения начального условия, если оно задано.

Применим метод неопределённых коэффициентов к рассмотренной выше задаче. Так как x ₀ = 0, то пишем

y = a + bx + cx ² + dx ³ + ex ⁴ …

y = b +2 cx +3 d x ² +4 e x ³ …

Подставляя x ₀ = 0, получаем в силу начального условия, что a=1.Производим подстановку ряда в уравнение y = y -2 x ² -3 x :

b+2cx+3d x² = a+bx+cx² +dx³ -2 x² -3x

Приравнивая коэффициенты при одинаковых степенях x, приходим к соотношениям:

a=b; c=(b-3)/2; d=(c-2)/3

И так мы получаем, что b=1, c= -1; d= -1.

3.2 Тестирование программы

Решим при помощи программызадачу, рассматриваемую в прошлом разделе:

Для этого подставим коэффициенты перед переменной x, во всех степенях начиная с наименьшей соответственно.

При решении двумя способами результаты совпали.

3.3 Руководство программисту

Для того чтобы программа работала быстро и эффективно не требуется мощных компьютеров и современных операционных систем. Ниже приведены минимальные параметры компьютера, которые нужны для работы:

· Центральный процессор: IntelPentium 166 MHz(рекомендуется P2 400 MHz)

· Операционныесистемы: Microsoft Windows 98, Windows Millennium (Me), Windows 2000, Windows ХР

· Оперативная память: 128 Mb (рекомендуемая 256 Mb)

· Памяти на жестком диске: 115 Mb (при компактной установке),

675 Mb (при полной установке), 580 Mb (при профессиональной установке),

480 Mb (при персональной установке)

· CD-ROM drive

Монитор с разрешением VGA и выше.

Заключение

Данная работа посвящена разработке алгоритма и программы решения задачи нахождения производной методом неопределённых коэффициентов. Сложность поставленной задачи обуславливается тем, что при нахождение производной данным методом, мы часто получаем выходное уравнение с многочленами при больших степенях. Решение такого уравнения может быть слишком долгим, что потребует больших затрат.

Рассмотренный метод неопределённых коэффициентов является одним из самых быстрых для поиска производной. Он лёгок для понимания и способен давать достаточно точные результаты.

Основные результаты работы сводятся к тому, что указывается важная роль применения численных методов, а в частности методов нахождения производной, направление развития существующих методов, обуславливается выбор метода.

Направление дальнейших исследований целесообразно развивать в разработке новых более точных и по возможности простых алгоритмов, которые бы заключали в себе все достоинства существующих методов, но исключали их недостатки. Новые методы должны быть максимально информативны, учитывающими те факторы, которые опускаются в уже существующих.

Список литературы

1.«Основы численных методов»-Л.И Турчак (1987г);

2. «Численные методы» Бохвалов Н.В.

Приложение A

#include iostream.h

double main(){

coutProgramma dli naxoshdenui neopredelennux koefficientovendl;

coutRukovodstvo:endl;

coutVvedite koeffichenti pered X, nachinai s naimenshey stepeni X-aendl;

coutPrimechanie:endl;

coutEsli v uravnenie otsutstvuet X c kakoy libo stepenu, ne bolshe 5-oy,endl;

coutto ego koefficent = 0endl;

coutUslovia:endl;

coutMaximalnai stepen X-a ne bolshe 5-oyendl;

coutMaximalnai stepen y-ka ne bolshe 1-oyendl;

coutx0=0 , c0=1endl;

int c0=1;

double c1,c2,c3,c4,c5,c6;

double a,c,e,g,j;

cina;

cinc;

cine;

cing;

cinj;

if(j!=0){

c1=c0;c2=(c1+a)/2;c3=(c2+c)/3;c4=(c3+e)/4;c5=(c4+g)/5;c6=(c5+j)/6;

coutPoluchinoe uravnenie:

y2=c1+c2x+c3x*x+c4x*x*x+c5x*x*x*x+c6x*x*x*x*xendl;}

else if(g!=0){

c1=c0;c2=(c1+a)/2;c3=(c2+c)/3;c4=(c3+e)/4;c5=(c4+g)/5;c5=(c4+g)/5;

coutPoluchinoe uravnenie:

y2=c1+c2x+c3x*x+c4x*x*xendl;}

else if(e!=0){

c1=c0;c2=(c1+a)/2;c3=(c2+c)/3;c4=(c3+e)/4;c5=(c4+g)/5;

coutPoluchinoe uravnenie:

y2=c1+c2x+c3x*xendl;}

else if(c!=0){

c1=c0;c2=(c1+a)/2;c3=(c2+c)/3;c4=0;c5=0;c6=0;}

else if(a!=0){

c1=c0;c2=(c1+a)/2;c3=0;c4=0;c5=0;c6=0;}

else {coutUravnenie smisla ne imeetendl;}

coutc1=c1endlc2=c2endlc3=c3endlc4=c4endlc5=c5endlc6=c6endl;

return 0;}

Приложение Б

Скачать архив с текстом документа