Разработка приложений в визуальной среде Delphi на языке программирования Object Pascal
СОДЕРЖАНИЕ: Содержание 1. Математические модели 3 1.1 Задача 1. Математическая модель 3 1.2 Задача 2. Математическая модель 4 2.2 Задача 2. Алгоритм решения 11 ВведениеСодержание
1.1 Задача 1. Математическая модель
1.2 Задача 2. Математическая модель
2.1 Задача 1. Алгоритм решения
2.2 Задача 2. Алгоритм решения
3. Описание основных операторов, процедур, функций и методов
Список использованных источников
Введение
Целью курсовой работы является приобретение навыков программирования и применения их на практике для решения вычислительных задач. Приложения курсовой работы разработаны в визуальной среде Delphi на языке программирования ObjectPascal.
Интегрированная среда разработки (IDE) - это среда, в которой разработчику предоставляется всё необходимое для написания, отладки, запуска и тестирования приложений. Она позволяет в кратчайшие сроки создавать действующие приложения, на ходу проектируя и видоизменяя их пользовательский интерфейс [1].
В состав IDE входит несколько элементов: редактор кода, отладчик, набор панелей инструментов, обширная библиотека компонентов, редактор изображений, инструментарий баз данных.
Среда Delphi- одна из первых систем, использующих технологию быстрой разработки приложений (RapidApplicationDevelopment- RAD) и технологию визуального конструирования (VisualDesign) [1]. Технология визуального конструирования содержит готовые компоненты, из которых строится интерфейс будущей программы.
Основные особенности среды Delphi: визуальное конструирование программ, использование готовых компонентов-заготовок для будущих программ, поддержка нескольких языков программирования, возможность создания программ под разные платформы, введение множества технологий, ускоряющих и облегчающих написание программ [1].
Задачами курсовой работы является: изучить основы работы в среде Delphi; изучить основные этапы решения задач на ЭВМ; разработать математические модели решения задач; изучить методы составления алгоритмов решения задач; проанализировать результаты работы программ на ЭВМ.
1. Математические модели
1.1 Задача 1. Математическая модель
В задаче по аналитической геометрии необходимо создать приложение для нахождения расстояния от данной точки до ближайшей стороны заданного треугольника. Для этого нужно рассмотреть уравнение прямой, проходящей через две точки, заданные координатами (х1 , у1 ) и (х2 , у2 ) в общем виде [2]:
Ax + By + C=0, (1.1)
А= у2 - у1 , (1.2)
В= х1 - х2, (1.3)
С= - х1 (у2 - у1 ) + у1 (х2 - х1 ). (1.4)
Расстояние от точки, заданной координатами (х4 , у4 ), до прямой, заданной уравнением (1.1), может быть определено так [2]:
d =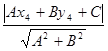 
. (1.5)
В задаче задаются вершины треугольника (х1 , у1 ), (х2 , у2 ), (х3 , у3 ) значит формулу (1.5) нужно применить, для нахождения расстояния к трем сторонам треугольника. А затем определить наименьшее из значений, что и будет искомым расстоянием.
Пусть стороны треугольника обозначим a,b,c. Найдем параметры уравнений сторон треугольника по формулам (1.2), (1.3), (1.4).
Для стороны а: a1=y2-y1; b1=x1-x2; c1= (-x1) (y2-y1) +y1 (x2-x1).
Для стороны b: a2=y3-y2; b2=x2-x3; c2= (-x2) (y3-y2) +y2 (x3-x2).
Для стороны c: a3=y1-y3; b1=x3-x1; c3= (-x3) (y1-y3) +y3 (x1-x3).
Расстояние от точки, заданной координатами (х4 , у4 ), до сторон треугольника a, b, c может быть определено по формуле (1.5):
d1 =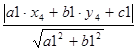
;
d2 =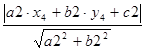
;
d3 =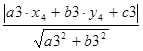
.
Определим систему ограничений для решения данной задачи. Если рассмотреть на формулу (1.5) нахождения расстояния от точки, заданной координатами (х4 , у4 ), до прямой, заданной уравнением (1.1), то необходимым и достаточным условием существования выражения является неравенство [2]:
0. (1.6)
Таким образом, применяя формулу (1.6) для решения задачи запишем систему ограничений:
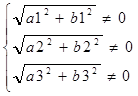. (1.7)
По условию задачи исходными данными являются координаты вершин треугольника, поэтому систему ограничений для данной задачи дополним условием существования треугольника:
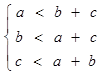. (1.8)
Определим длины сторон треугольника по формуле расстояния между двумя точками [2]:
d=
. (1.9)
Для треугольника со сторонами a,b,c формула (1.9) имеет вид:
a=,
b=
,
c=
.
Вычисленные длины сторон треугольника применим к системе ограничений (1.8). Таким образом, в задаче рассматривается две системы ограничений (1.7), (1.8) для необходимого и достаточного условия существования решения.
1.2 Задача 2. Математическая модель
Во второй задаче по теоретической механике необходимо создать приложение, которое будет отображать визуальное перемещение объектов в соответствии с кинематической схемой, рисунок 1 (Кинематическая схема).
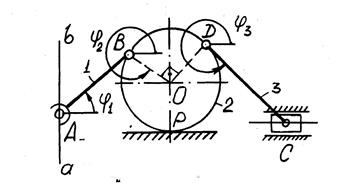
Рисунок 1 - Кинематическая схема
На данном механизме (рисунок 1 (Кинематическая схема)) имеется одна неподвижная опора, на которой находится подвижный барабан, к нему на шарнирах прикреплены стержни [5]. Один стержень связан шарниром с ползуном и движется вдоль горизонтальной направляющей [5]. Другой стержень шарниром соединен с неподвижной осью и движется в вертикальном направлении [5].
В качестве переменной, определяющей положение, механизма задана переменная W. В таком случае положение механизма однозначно определяется переменной W. В зависимости от изменения положения вращающегося звена изменяется положение механизма в целом. Вращающееся звено может изменять положение в первой четверти декартовой системы координат. Зададим точки, определяющие положение механизма, рисунок 2 (Точки, определяющие положение механизма).
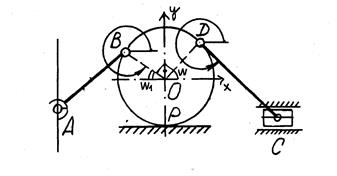
Рисунок 2 - Точки, определяющие положение механизма
На основании схемы приведенной на рисунке 2 (Точки, определяющие положение механизма), составим математическую модель, описывающую положение механизма в зависимости от изменения угла W. В связи с изменением геометрических параметров механизма на плоскости, принимаем за текущую декартову систему координат с направлением осей X и Y.
Радиус окружности барабана задает сам пользователь в форме, причем OD = OB = R. Координаты точки О (х0, у0) задаются в программе. Размер стержней принимается за постоянную величину и определяется пользователем. Угол W задается пользователем в форме. Изменяя значение угла W, будет изменяться положение механизма.
Определим координаты точки D.
Проекция точки D на ось х равна [2]: ODx = OD cosW= R cosW.
Проекция точки D на ось y равна [2]: ODy = OD sinW= R sinW.
Определим координаты точки B. Для этого определим величину угла W1. Исходя из рисунка 2 (Точки, определяющие положение механизма) видно, что весь угол является развернутым [2] и равен 1800 , исходя, из этого можно определить величину угла W1:
W1=1800 - 900 - W = 900 - W.
Проекция точки B на ось х равна [2]: OBx = OB cos (90 0 - W) = R sinW.
Проекция точки B на ось y равна [2]: OBy = OB sin (90 0 - W) = R cosW.
Исходя из того, что длинна стержней АВ и DC задана константой в программе, определим координаты точек С и А.
Координаты точки C.
Проекция точки С на ось х равна: DСx = х0 +DС cosW.
Проекция точки С на ось y равна: DСy = у0+DС.
Определим координаты точки А.
Проекция точки А на ось х равна: АВx = х0 - АВ.
Проекция точки А на ось y равна: АВy = у0+АВ cosW1.
2. Алгоритмы решения задач
Алгоритм - точное предписание, определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату [3].
Основные свойства алгоритма:
определённость: указания, составляющие алгоритм, должны быть четкими и однозначными, не допускать произвольного или двоякого толкования;
дискретность: возможность поэтапной детализации алгоритма путем разложения любой сложной структуры на ряд простых, строго очерченных действий;
конечность: вычислительный процесс должен задаваться конечной последовательностью действий;
результативность: конечная последовательность действий должна заканчиваться выдачей результатов или сообщением о невозможности решить задачу;
рациональность: вычислительный процесс должен привести к результату за наименьшее время при минимальном использовании ресурсов компьютера;
массовость: алгоритм может использоваться для решения множества однотипных задач [3].
Разработанные алгоритмы могут быть представлены на физическом носителе информации различными способами:
словесный (вербальной форме): средствами языка человеческого общения с тщательно отобранным набором слов и фраз;
структурно-стилизованный: языком псевдокодов;
графический: схемами из графических блок - символов;
программный: текстами программ [3].
2.1 Задача 1. Алгоритм решения
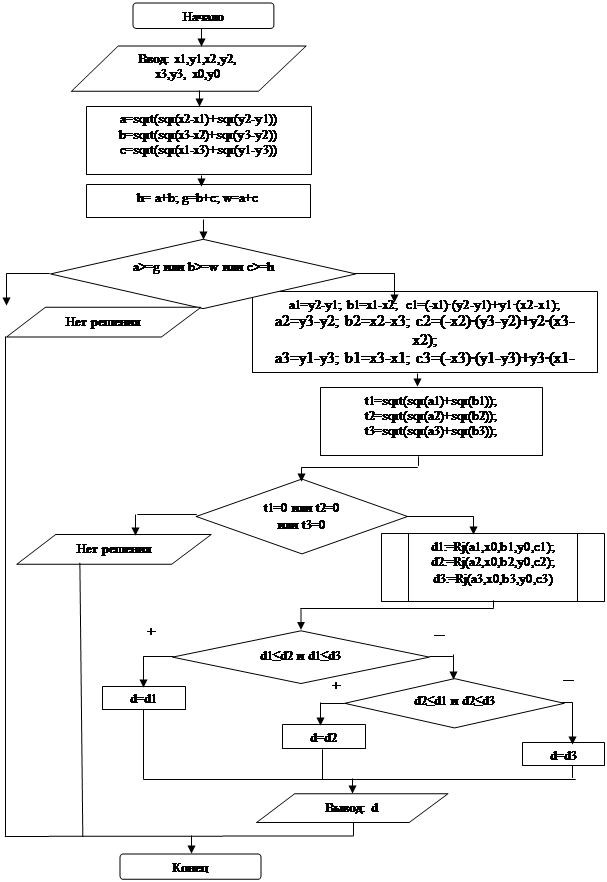
Для решения задачи 1 был разработан алгоритм, представленный в графическом виде. На рисунке 3 (Блок-схема решения задачи1) представлен алгоритм решения задачи в виде блок-схемы, а на рисунке 4 (Блок-схема подпрограммы задачи1) представлена блок-схема подпрограммы для вычисления расстояния до ближайшей стороны.
+
+
Рисунок 3 - Блок-схема решения задачи 1
При решении задач часто приходится выполнять многократные вычисления не только по одним и тем же формулам, но и по одним и тем же алгоритмам, в которых изменяются значения только некоторых переменных. В этом случае повторяющиеся части целесообразно оформлять в виде отдельных модулей - подпрограмм, дополняющих основную программу. Использование подпрограмм не только освобождает от переписывания повторяющихся фрагментов программного текста, но и улучшает наглядность и структуру программы, позволяет перейти к модульному программированию и оптимизировать программу, создать личную библиотеку программных модулей. В Delphi подпрограммы оформляют в виде процедур и функций, которые входят в основную программу путем соответствующего описания. Для решения задачи была использована подпрограмма, оформленная в виде функции пользователя, рисунок 4 (Блок-схема подпрограммы задачи 1).
Функция пользователя это один из способов оформления подпрограммы или фрагмента программы, предназначенного для решения части общей задачи [4]. Функция пользователя предназначена для вычисления только одного значения и передается в основную программу как значение одной переменной с именем этой функции. Параметры, записываемые в обращении к функции, называются фактическими, а параметры, указанные в ее описании, формальными. В теле функции обязательно должен быть хотя бы один оператор присваивания, где в левой части стоит имя функции, а в правой - её значение. Иначе значение функции не будет определено.
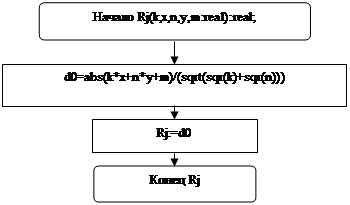
Рисунок 4 - Блок-схема подпрограммы задачи 1
2.2 Задача 2. Алгоритм решения
На основании созданной математической модели задачи 2 составим алгоритм программного приложения.
Алгоритм приложения задачи 2 является линейным, в нём операции выполняются последовательно одна за другой, в естественном и единственном порядке следования. Все операции имеют последовательное соединение логической связью передачи информационных потоков [3].
Для простых приложений не требуются блок - схемы алгоритмов. Составим алгоритм в вербальной форме.
В связи с изменением геометрических характеристик системы в зависимости от переменной W, алгоритм предполагает наличие следующих действий:
ввод значения радиуса барабана (R);
определение констант (размеры стержней АВ и СD);
определение значения угла W;
определение положения точки начала координат О (х0, у0);
определение значения переменной W1;
определение координат точек, которые определяют положение механизма;
производим рисование элементов на экране;
закрытие программного приложения.
3. Описание основных операторов, процедур, функций и методов
При написании программного кода задачи 1 использовался условный оператор. Он позволяет проверить некоторое условие и в зависимости от результатов проверки выполнить то или иное действие. Таким образом, условный оператор - это средство ветвления вычислительного процесса.
Структура условного оператора имеет следующий вид [1]:
if условие then оператор1 else оператор2,
где: if/ then/ else - зарезервированные слова (если, то, иначе);
условие - произвольное выражение логического типа;
оператор1, оператор2 - любые операторы языка Object Pascal.
Условный оператор работает по следующему алгоритму. Вначале вычисляется условное выражение условие. Если результат есть True (истина), то выполняется оператор1, а оператор2 пропускается; если результат есть False (ложь), наоборот, оператор1 пропускается, а выполняется оператор2. Условными называются выражения, имеющие одно из двух возможных значений: истина или ложь. Такие выражения чаще всего получаются при сравнении переменных с помощью операций отношения =, , , =, , =. Сложные логические выражения составляются с использованием логических операций and (логическое И), or (логическое ИЛИ) и not (логическое НЕ).
В процессе создания программного приложения задачи1 использовались следующие функции:
функция преобразования типа
StrToFloat (const S: string): Extended;
преобразует строку S в вещественное число [4]. Строка должна содержать знак, цифры и десятичный разделитель в порядке, характерном для записи десятичных дробей. Также строка может содержать мантиссу, состоящую из знака, буквы Е и целого числа. Пробелы в начале и в конце строки игнорируются. Если S имеет другой формат, функция возвращает сообщение об ошибке;
функция обратного преобразования типа
FloatToStr (Value: Extended): String;
преобразует вещественное число в строку, возвращаемый результат типа string [4]. Строка, параметр использовать необязательно. При указании параметра задается формат отображения;
математическая функция
Abs (n);
абсолютное значение n [1] ;
математическая функция
Sqrt (n);
квадратный корень из n [1] (n 0);
математическая функция
Sqr (n);
возведение в квадрат n [1].
В приложении задачи 1 использованы методы обработки событий, происходящих на форме, код которых создан во время работы приложения:
procedure Button1Click (Sender: TObject); - нажатие на кнопку Button1;
procedure Button2Click (Sender: TObject); - нажатие на кнопку Button2;
procedure Button3Click (Sender: TObject); - нажатие на кнопку Button3.
Для определения расстояния до ближайшей стороны в задаче 1 была написана пользовательская функция function Rj (k, x, n, y, m: real): real;.
В процессе создания программного приложения задачи 2 использовались следующие функции:
функция преобразования типа
StrToInt (const S: string): Integer;
преобразует строку S, в которую записано целое число, в целочисленный тип [4] ;
функция преобразования типа
Round (x: real): integer;
преобразует вещественное число в целое [1] ;
математическая функция Sin (a); - синус угла а, заданного в радианах [1] ;
математическая функция Cos (a); - косинус угла а, заданного в радианах [1].
В приложении задачи 2 использованы методы обработки событий, происходящих на форме, код которых создан во время работы приложения:
procedure Button1Click (Sender: TObject); - нажатие на кнопку Button1;
procedure SpinEdit1Change (Sender: TObject); - изменение содержимого SpinEdit.
Методы объекта Canvas, обеспечивающие рисование на элементах формы:
MoveTo (x,y) - перемещает в указанную позицию (x,y) карандаш, не вычерчивает никаких графических примитивов;
LineTo (x,y) - рисует линию, рисование осуществляется из текущей позиции карандаша в позицию (х, у);
Rectangle (x1,y1,x2,y2) - рисует прямоугольник, параметры x1, y1, x2, y2 - координаты находящихся на одной диагонали углов прямоугольника;
Ellipse (x1,y1,x2,y2) - рисует эллипс, параметры x1, y1, x2, y2 - координаты диагональных углов области, внутри которой вычерчивается эллипс;
TextOut (x,y, Текст); - выводит текст на графическую поверхность, параметры (х, у) задают положение текста на экране, параметр Текст содержит строку текста, которую необходимо отобразить [1].
При рисовании графических примитивов использовался объект карандаш (Canvas. Pen), с помощью него прорисовка линий осуществлялась с различной толщиной и с различным стилем [1]:
Pen. Style: =const; - определяет вид линии (задается специальными константами: psSolid- сплошная линия, psDot- пунктирная линия с короткими штрихами, psDash- пунктирная линия с длинными штрихами);
Pen. Width: =числовое значение в пикселях; - задает толщину выводимой линии в пикселях.
4. Текст приложений
Программный код разработанного приложения к задаче 1.
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls,Math;
type
TForm1 = class (TForm)
Button1: TButton;
Button2: TButton;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Edit4: TEdit;
Edit5: TEdit;
Edit6: TEdit;
Edit7: TEdit;
Edit8: TEdit;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Label6: TLabel;
Label8: TLabel;
Button3: TButton;
Label9: TLabel;
Label11: TLabel;
Label12: TLabel;
Label13: TLabel;
Label14: TLabel;
Label15: TLabel;
procedure Button2Click (Sender: TObject);
procedure Button1Click (Sender: TObject);
procedure Button3Click (Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *. dfm}
procedure TForm1. Button2Click (Sender: TObject);
begin
close;
end;
procedure TForm1. Button3Click (Sender: TObject);
begin
Label15. Caption: = ();
end;
procedure TForm1. Button1Click (Sender: TObject);
var
x1,x2,x3,x0,y1,y2,y3,y0: real;
a,b,c,a1,b1,c1,a2,b2,c2,a3,b3,c3,t1,t2,t3: real;
d1,d2,d3,d: real;
h,g,w: real;
// подпрограмма определения расстояния до ближайшей стороны
function Rj (k,x,n,y,m: real): real;
var
d0: real;
begin
d0: =abs (k*x+n*y+m) / (sqrt (sqr (k) +sqr (n)));
Rj: =d0;
end;
begin
// ввод координат вершин треугольника
x1: =strtofloat (edit1. text);
y2: =strtofloat (edit2. text);
x2: =strtofloat (edit3. text);
y2: =strtofloat (edit4. text);
x3: =strtofloat (edit5. text);
y3: =strtofloat (edit6. text);
// ввод координат точки
x0: =strtofloat (edit7. text);
y0: =strtofloat (edit8. text);
// вычисление длин сторон треугольника
a: =sqrt (sqr (x2-x1) +sqr (y2-y1));
b: =sqrt (sqr (x3-x2) +sqr (y3-y2));
c: =sqrt (sqr (x1-x3) +sqr (y1-y3));
// проверка условий существования треугольника
h: = a+b; g: =b+c; w: =a+c;
if ( (a=g) or (b=w) or (c=h)) then Label15. Caption: =Нет решения
elsebegin
// вычисление параметров уравнений сторон треугольника
a1: =y2-y1; b1: =x1-x2; c1: = (-x1) * (y2-y1) +y1* (x2-x1);
a2: =y3-y2; b2: =x2-x3; c2: = (-x2) * (y3-y2) +y2* (x3-x2);
a3: =y1-y3; b1: =x3-x1; c3: = (-x3) * (y1-y3) +y3* (x1-x3);
t1: =sqrt (sqr (a1) +sqr (b1));
t2: =sqrt (sqr (a2) +sqr (b2));
t3: =sqrt (sqr (a3) +sqr (b3));
// проверка условия существования формулы для нахождения кратчайшего расстояния
if ( (t1=0) or (t2=0) or (t3=0)) then Label15. Caption: =Нет решения
elsebegin
// вычисление кратчайшего расстояния с помощью подпрограммы к трем сторонам треугольника
d1: =Rj (a1,x0,b1,y0,c1);
d2: =Rj (a2,x0,b2,y0,c2);
d3: =Rj (a3,x0,b3,y0,c3);
// нахождение наименьшего значения
if ( (d1=d2) and (d1=d3)) then d: =d1 else
if ( (d2=d1) and (d2=d3)) then d: =d2 else d: =d3;
end;
Label15. Caption: =d=+floattostr (d) +см;
end; end;
end.
Программный код разработанного приложения к задаче2.
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, ExtCtrls, Spin, Math;
type
TForm1 = class (TForm)
Panel1: TPanel;
Label1: TLabel;
Label3: TLabel;
Button1: TButton;
Panel2: TPanel;
Image1: TImage;
SpinEdit1: TSpinEdit;
Label2: TLabel;
Edit1: TEdit;
procedure Button1Click (Sender: TObject);
procedure SpinEdit1Change (Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *. dfm}
procedure TForm1. Button1Click (Sender: TObject);
begin
close;
end;
procedure TForm1. SpinEdit1Change (Sender: TObject);
var
// координаты основных точек определяющих положение механизма
xd,xb,xa,xc,x0,yd,yb,ya,yc,y0,o1,o2,o3,o4: integer;
// значения радиуса барабана и срержней
od,dc,ab,ob,R: integer;
// углы
w,w1: real;
begin
// ввод значения радиуса барабана
R: =StrToInt (Edit1. Text);
od: =round (R);
ob: =round (od);
// задание размеров стержней
dc: =90;
ab: =70;
// определение значения угла W
W: =spinedit1. value*pi/180;
// задание точки определяющей начало координат
x0: =round (form1. image1. width/2);
y0: =round (form1. image1. height/2);
// вычисление значения угла W1
w1: =pi-pi/2-w;
// вычисление координат точек определяющих положение механизма
xd: =x0+round (od*cos (w));
yd: =y0-round (od*sin (w));
xb: =x0-round (ob*cos (w1));
yb: =y0-round (ob*sin (w1));
xc: =x0+round (dc*cos (w));
yc: =y0+round (dc);
xa: =x0-round (ab);
ya: =y0+round (ab*cos (w1));
o1: =round (x0-od);
o2: =round (y0-od);
o3: =round (x0+od);
o4: =round (y0+od);
// рисование элементов системы на экране и подписи основных точек механизма
form1. image1. picture: =nil;
with form1. image1. canvas do
begin
ellipse (o1,o2,o3,o4);
ellipse (xd-3, yd-3, xd+3, yd+3);
ellipse (xb-3, yb-3, xb+3, yb+3);
moveto (x0,y0);
Pen. Style: =psDot;
lineto (xd,yd);
moveto (x0,y0);
lineto (xb,yb);
Pen. Style: =psSolid;
moveto (xc,yc);
Rectangle (xc+10,yc+8,xc-10,yc-8);
Lineto (xc+400,yc);
lineto (xc-400,yc);
moveto (xc,yc+10);
Pen. Width: =2;
lineto (400,yc+10);
lineto (150,yc+10);
moveto (xc,yc-10);
lineto (400,yc-10);
lineto (150,yc-10);
moveto (xd,yd);
Pen. Width: =1;
lineto (xc,yc);
ellipse (xc-3, yc-3, xc+3, yc+3);
moveto (xb,yb);
lineto (xa,ya);
ellipse (xa-3, ya-3, xa+3, ya+3);
moveto (xa,ya);
Pen. Width: =2;
lineto (xa,ya+400);
lineto (xa,ya-400);
Pen. Width: =1;
moveto (xd+5,yd-8);
Textout (xd+5,yd-8,D);
moveto (xb-5,yb-15);
Textout (xb-5,yb-15,B);
moveto (xa-15,ya-8);
Textout (xa-15,ya-8,A);
moveto (xc+10,yc-25);
Textout (xc+10,yc-25,C);
moveto (x0+1,y0+1);
Textout (x0+1,y0+1,O);
moveto (x0,y0+R);
Textout (x0,y0+R+3,P);
Pen. Width: =2;
Lineto (x0+20,y0+R);
Lineto (x0-20,y0+R);
end;
end;
end.
5. Формы приложений
Одним из основных элементов приложения является форма, из которой пользователь управляет событиями, происходящими во время работы приложения.
Форма, на которой размещаются компоненты, является основой большинства приложений Delphi. Она представляет собой окно создаваемого приложения, определяет интерфейс приложения для общения с пользователем и непосредственно дает возможность редактировать взаимное расположение и свойства (цвет, размер) элементов интерфейса для придания ему большей эргономичности [4].
Для решения задачи 1 в Delphi было разработано приложение. Вид окна приложения до выполнения вычислений представлен на рисунке 5 (Исходная форма приложения задачи 1).
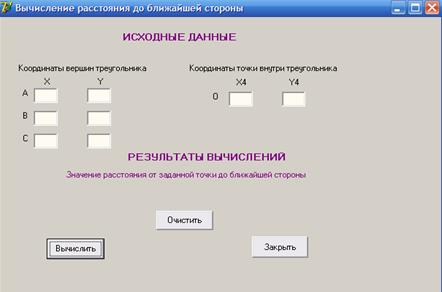
Рисунок 5 - Исходная форма приложения задачи 1
На рисунке 6 (Форма приложения с результатами вычислений задачи 1) представлена форма приложения с результатами вычислений. Различные варианты работы алгоритма приложения к задаче 1 отображены на рисунке А.9 (Форма приложения с результатами вычислений задачи 1), где треугольник не существует и на рисунке В.10 (Форма приложения с результатами вычислений задачи 1), где точка располагается на одной из вершин треугольника.
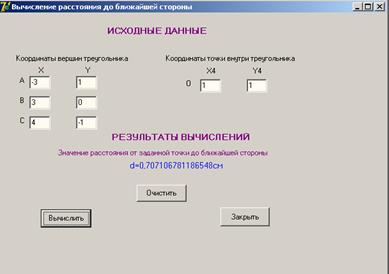
Рисунок 6 - Форма приложения с результатами вычислений задачи 1
На форме расположены следующие компоненты:
Label- компоненты для вывода текста (13 шт.);
Edit- поля редактирования (8 шт.);
Button- кнопки (3 шт.).
Для решения задачи 2 в Delphi было разработано приложение работы кинематической схемы. Исходный вид окна приложения представлен на рисунке 7 (Исходная форма приложения задачи 2), а на рисунке 8 (Форма приложения кинематической схемы) представлена форма приложения с изображением кинематической схемы, если радиус барабана R=30. Другие варианты работы алгоритма приложения кинематической схемы представлены на рисунке С.11 (Форма приложения кинематической схемы), где радиус барабана R= 40 и на рисунке D.12 (Форма приложения кинематической схемы), где радиус барабана R= 20.
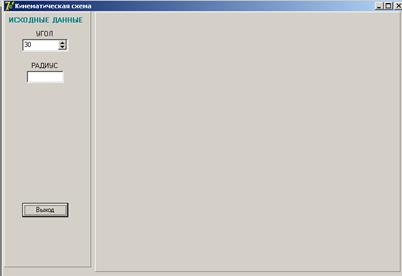
Рисунок 7 - Исходная форма приложения задачи 2
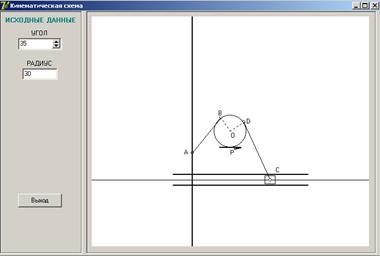
Рисунок 8 - Форма приложения кинематической схемы
На форме размещены следующие компоненты:
Panel1, Panel2 - это контейнер для других компонентов и позволяет легко управлять компонентами, которые находятся на панели (компоненты, находящиеся на панели, наследуют свойства компонента Panel);
Button1 - командная кнопка для закрытия приложения;
Edit1 - поле редактирования, содержащее значение вводимой величины;
SpiEdit1 - строка, содержащая числовое значение переменной W;
Label1, Label2, Label3 - компоненты для вывода текста, содержащие текст и несущие информацию о назначении других компонентов;
Image1 - место для рисования схемы.
Заключение
При выполнении курсовой работы были закреплены навыки программирования. Изучены способы применения их на практике для решения вычислительных задач в визуальной среде Delphi на языке программирования ObjectPascal.
В ходе выполнения работы были написаны приложения для двух задач разного типа.
Решение первой задачи основывается на организации вычислительного процесса для нахождения расстояния от заданной точки лежащей внутри заданного треугольника до ближайшей стороны этого треугольника. При решении используется программирование алгоритмов разветвляющейся структуры, реализующихся с помощью оператора условного перехода IF, который служит для изменения порядка выполнения операторов в зависимости от какого-то условия.
В первой задаче поставлены два условия:
система ограничений, формулы (1.8), проверки существования треугольника;
система ограничений, формулы (1.7), существования формулы (1.5) для расчета наименьшего расстояния до сторон треугольника.
Решение второй задачи предполагает использовать более широкий спектр базовых компонент при программировании:
Panel;
Button;
Edit;
SpiEdit;
Label;
Image.
Реализация заданной кинематической схемы позволяет изучить основы работы с графикой в визуальной среде Delphi.
Изучены методы вычерчивания основных графических примитивов:
MoveTo (x,y);
LineTo (x,y);
Rectangle (x1,y1,x2,y2);
Ellipse (x1,y1,x2,y2)).
Метод вывода текста на графическую поверхность - TextOut (x,y,Текст). Изучены свойства основного инструмента, позволяющего рисовать на графической поверхности - карандаш (Pen).
Задачами курсовой работы являлось:
изучить основы работы в среде Delphi;
изучить основные этапы решения задач на ЭВМ;
разработать математические модели решения задач;
изучить методы составления алгоритмов решения задач;
проанализировать результаты работы программ на ЭВМ.
Поставленные задачи в ходе выполнения курсовой работы выполнены в полном объеме.
Список использованных источников
1. Шупрута В.В. Delphi 2005. Учимся программировать / В.В. Шупрута. - М.: НТ Пресс, 2005. - 352с.;
2. Воднев В.Т. Основные математические формулы: справочник / В.Т. Воднев, А.Ф. Наумович, Н.Ф. Наумович. - Мн: Высш. шк., 2000. - 269с.;
3. Прищепов М.А. Программирование на языках Basic, Pascal и ObjectPascal в среде Delphi / М.А. Прищепов, Е.В. Севернёва, А.И. Шакирин. - Мн.: ТетраСистемс, 2006. - 320с.;
4. Бескоровайный И.В. Азбука Delphi: программирование с нуля / И.В. Бескоровайный. - Новосибирск: Сиб. унив. изд-во, 2008. - 112с.;
5. Яблонский А.А. Курс теоретической механики / А.А. Яблонский, В.М. Никифорова. - М.: Высш. шк., 1977. - 368с. с ил.;
6. Фаронов В.В. Турбо Паскаль 7.0/В.В. Фаронов. - М.: Нолидж, 2006. - 616с.;
7. Тейксейра С. BorlandDelphi6/С. Тейксейра, К. Пачеко. - М.: Нолидж, 2002. - 1120с.;
8. Фаронов В.В. Профессиональная работа в Delphi6/В.В. Фаронов. - М.: Нолидж, 2002. - 320 с.;
9. Культин И.Б. Программирование в TurboPascal 7.0 и Delphi / И.Б. Культин. - СПб.: ВНV, 2003. - 462с.;
10. Яблонский А.А. Сборник заданий для курсовых работ по теоретической механике: Учебное пособие для технических вузов / А.А. Яблонский, С.С. Норейко, С.А. Вольфсон. - М.: Интеграл-Пресс, 2008. - 384с.;
11. Краснов М. Графика в проектах Delphi / М. Краснов. - СПб.: БХВ-Петербург, 2000. - 352с. .
Приложения
Приложение А
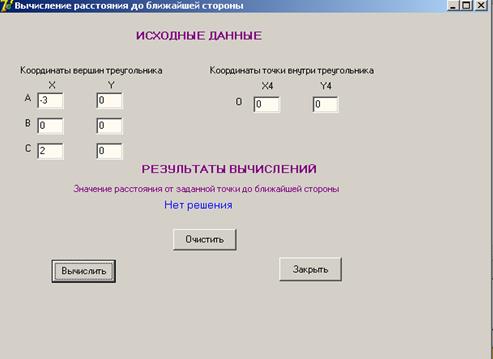
Рисунок 9 - Форма приложения с результатами вычислений задачи 1
Приложение В
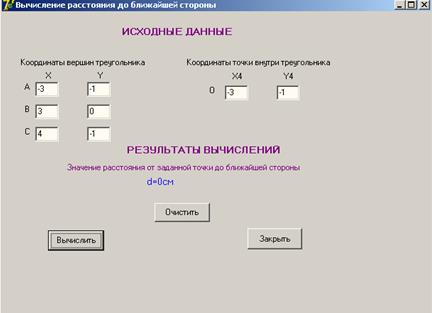
Рисунок 10 - Форма приложения с результатами вычислений задачи 1
Приложение С
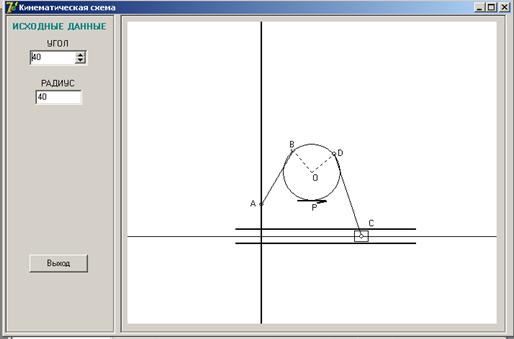
Рисунок 11 - Форма приложения кинематической схемы
Приложение D
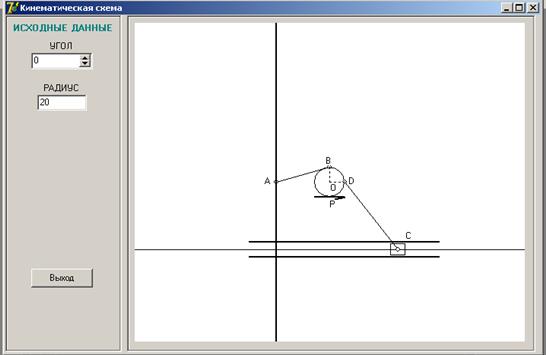
Рисунок 12 - Форма приложения кинематической схемы