Разработка сменного модуля для изучения соединения типа Звезда
СОДЕРЖАНИЕ: Особенности соединения типа звезда, порядок проектирования и изготовления сменного модуля для проведения лабораторных работ по его изучению. Понятие четырехполюсников и порядок определения режимов их работы, методика расчета специальных коэффициентов.КУРСОВАЯ РАБОТА
на тему:
«Разработка сменного модуля для изучения
соединения типа «Звезда»»
Чита 2009
Содержание
Введение
1. Теоретическая часть
1.1 Четырехполюсники и их уравнения
1.2 Режимы четырехполюсников
1.3 Коэффициенты четырехполюсников
2. Практическая часть
2.1 Проектирование модуля
2.2 Изготовление модуля
3. Расчетная часть
Литература
Введение
Целью данной курсовой работы является проектирование и изготовление сменного модуля для проведения лабораторных работ по изучению соединения типа «звезда».
На практике часто встречаются соединения элементов, которые нельзя свести только к последовательному или параллельному соединению. Примером подобного соединения являются соединения многолучевой звездой и многоугольником. Наиболее часто встречаются случаи трёхлучевой звезды и треугольника.
В данной работе соединение трёхлучевой звездой реализовано в симметричном Т-образном четырехполюснике (рис. 1.1).
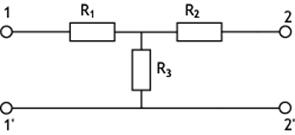
Рис. 1.1
1. Теоретическая часть
1.1 Четырехполюсники и их уравнения

Рис. 1.2
Условное изображение четырехполюсника показано на рис. 1.2. Одну пара выводов из четырех назовем первичной , а другую вторичной и обозначим соответственно цифрами 1–1 и 2–2 . Для расчета режима выберем положительные направления напряжений и токов, показанные на рис. 1.2.
Будем считать, что источники питания, приемники и любые участки цепи с парными выводами могут присоединяться только к выводам четырехполюсника, которые обозначены одинаковыми цифрами. Такие четырехполюсники называют проходными .
Все четырехполюсники подразделяются на две группы: пассивные и активные. В пассивных четырехполюсниках нет зависимых или независимых источников напряжения (ЭДС) или тока, активные четырехполюсники содержат зависимые или независимые источники.
Для исследования четырехполюсников необходимо, прежде всего, установить зависимости между четырьмя величинами, определяющими режим его работы: напряжениями и токами на первичных и вторичных выводах.
Зависимости между двумя напряжениями и двумя токами, определяющими режим на первичных и вторичных выводах, могут быть записаны в различной форме. Если считать две из указанных величин заданными, то две другие величины будут связаны с ними системой двух уравнений, которые называются уравнениями четырехполюсника .

Рис. 1.3

Рис. 1.4
Например, если к вторичным выводам четырехполюсника подключен приемник с сопротивлением нагрузки Z
2н
, а к первичным – источник ЭДС Е1
(рис. 1.3), то при заданном напряжении на выводах приемника U2
и токе ![]() можно определить необходимое напряжение источника питания на первичных выводах U
1
=
E
1
и ток источника I
1
по уравнению типа А:
можно определить необходимое напряжение источника питания на первичных выводах U
1
=
E
1
и ток источника I
1
по уравнению типа А:
![]() ;
;
![]() ,
,
или в матричной форме
![]() ,
,
где ![]() и
и ![]() – матрицы-столбцы напряжения и тока соответственно на первичных и вторичных выводах;
– матрицы-столбцы напряжения и тока соответственно на первичных и вторичных выводах;
![]() – квадратная матрица коэффициентов.
– квадратная матрица коэффициентов.
В этих уравнениях коэффициенты A11 , А12 , А21 , А22 определяют сам четырехполюсник и зависят от схемы соединения и параметров составляющих четырехполюсник элементов электрической цепи; A11 и А22 – безразмерные коэффициенты; A12 имеет размерность сопротивления, а А21 – проводимости.
Всего можно записать шесть различных по форме, но по существу эквивалентных, т.е. математически равносильных, пар уравнений (число сочетаний из четырех по два).
Уравнения типа Y
![]()
или
![]() , где все коэффициенты – проводимости.
, где все коэффициенты – проводимости.
Уравнения типа Z
![]()
или
![]() с коэффициентами – сопротивлениями.
с коэффициентами – сопротивлениями.
Уравнения типа H
![]()
или
![]()
с коэффициентами, размерность которых, как и в первых трёх системах уравнений, непосредственно следует из самой записи уравнений.
Уравнения типа G
![]()
или
![]() .
.
Уравнения типа B
![]()
или
![]() .
.
1.2 Режимы четырехполюсников
При расчете режима работы четырехполюсника с применением различных типов уравнений принято выбирать положительные направления токов неодинаковыми (рис. 1.2). Положительные направления токов по рис. 1.3 (I 1 и I 2 ) часто выбирают для пассивных четырехполюсников с источником питания на первичных – входных выводах и приемником с сопротивлением Z2н на вторичных выходных выводах и записи уравнений типа А.
Входные сопротивления. Отношение напряжения U1 к току I1 при питании четырехполюсника со стороны первичных выводов и сопротивлении нагрузки Z2н на вторичных (рис. 1.3) называется входным сопротивлением четырехполюсника со стороны первичных выводов Z1вх . При питании четырехполюсника со стороны вторичных выводов и сопротивлении нагрузки Z1н на первичных (рис. 1.4) отношение напряжения U2 к току I2 – это входное сопротивление четырехполюсника со стороны вторичных выводов Z2вх .
Входное сопротивление четырехполюсника определяет режим работы источника питания и зависит от структуры и параметров составляющих четырехполюсник элементов, т.е. коэффициентов четырехполюсника, а также от сопротивления нагрузки, т.е. сопротивления приемника.
Для определения входных сопротивлений Z1вх и Z2вх можно воспользоваться любым из типов уравнений, однако наиболее простые выражения получаются, если соответственно выбрать уравнения типов А и В:
![]() ;
;
![]() ;
;
В частном случае при отключенном или закороченном приемнике входные сопротивления характеризуют только сам четырехполюсник, а следовательно, зависят только от его коэффициентов.

Рис. 1.5
При питании со стороны первичных выводов и коротком замыкании вторичных (рис. 1.5), т.е. при Z2н = 0, входное сопротивление
![]()
При холостом ходе на вторичных выводах, т.е. при ![]() , входное сопротивление
, входное сопротивление
![]()
Сопротивления короткого замыкания и холостого хода четырехполюсника однозначно определяются его коэффициентами.
Режим работы четырехполюсника, как и любой электрической цепи, можно характеризовать передаточными функциями при заданном сопротивлении приемника, т.е. в отличие от коэффициентов четырехполюсника передаточная функция зависит не только от структуры и параметров составляющих четырехполюсник элементов, но и от параметров приемника. Если, например, источник питания подключен к первичным выводам (см. рис. 1.3), то при сопротивлении нагрузки Z
2н
можно составить различные передаточные функции, например ![]() и т.д.
и т.д.
1.3 Коэффициенты четырехполюсников
Коэффициенты уравнений постоянны и определяются только структурой четырехполюсника и параметрами составляющих его элементов, а не параметрами источника питания и приемника. С точки зрения режима на первичных и вторичных выводах четырёхполюсники, имеющие одинаковые значения коэффициентов, неотличимы, т.е. эквивалентны, хотя их внутренняя структура может быть совсем различной.
Таким образом, можно утверждать, что четырёхполюсник задан, если известны его коэффициенты.
Уравнения четырёхполюсника показывают, что проходной активный неавтономный или пассивный четырёхполюсник задаётся четырьмя коэффициентами любого из типов уравнений. Поэтому матрица коэффициентов одного из типов уравнений может быть выражена через матрицу коэффициентов любого другого типа уравнений.
Коэффициенты уравнений четырёхполюсника называют ещё его первичными параметрами. Каждый из первичных параметров имеет простой физический смысл. Например, по ![]() при
при ![]() (в режиме холостого хода на вторичных выводах), т.е.
(в режиме холостого хода на вторичных выводах), т.е. ![]() – входное сопротивление, измеренное на первичных выводах при разомкнутых вторичных. Если известна схема четырёхполюсника и значения составляющих его элементов, то любой из коэффициентов может быть определён расчетом.
– входное сопротивление, измеренное на первичных выводах при разомкнутых вторичных. Если известна схема четырёхполюсника и значения составляющих его элементов, то любой из коэффициентов может быть определён расчетом.
Симметричный четырехполюсник.
Четырехполюсник, у которого при взаимной замене первичных выводов и вторичных выводов режимы источника питания и приемника не изменяются, называется симметричным
. У такого активного неавтономного четырехполюсника не четыре, а три независимых коэффициента, а у пассивного два. Например, как было показано выше, при питании четырехполюсника со стороны первичных выводов и разомкнутых вторичных Z1х
=Z11
. При питании со стороны вторичных выводов и разомкнутых первичных у симметричного четырехполюсника должно быть такое же входное сопротивление Z2х
=Z1х.
Из уравнений ![]() или
или ![]() при I1
=0 получаем Z22
=U2
/I2
=Z2х
, и, следовательно,
при I1
=0 получаем Z22
=U2
/I2
=Z2х
, и, следовательно, ![]() .
.
Такие же рассуждения приводят к равенствам
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Если два Г-образных четырехполюсника соединить соответственно друг с другом выводами 1 и 1, то получится симметричный Т-образный четырехполюсник.
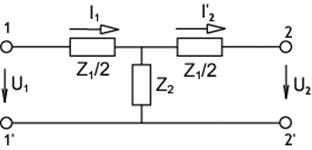
Рис. 1.6
Найдем коэффициенты уравнений типа А симметричного Т-образного четырехполюсника (рис. 1.6).
При холостом ходе на вторичных выводах (I2 =0) из рис. 1.6 следует, что
![]() ;
; ![]() или
или ![]() . Сравнив эти выражения с уравнениями при
. Сравнив эти выражения с уравнениями при ![]() , определим
, определим
![]() ;
; ![]() .
.
При коротком замыкании вторичных выводов (![]() ) из рис. 1.6 следует, что
) из рис. 1.6 следует, что ![]() или
или ![]() ;
;
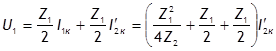 .
.
Сравнив эти выражения с уравнениями при U2 =0, найдем
![]() ;
; ![]() , т.е.
, т.е. ![]() , как и должно быть у симметричного четырехполюсника.
, как и должно быть у симметричного четырехполюсника.
Экспериментальное определение коэффициентов и входных сопротивлений.
Первичные параметры каждого данного четырехполюсника могут быть определены экспериментально при измерении режима (напряжений и токов) на первичных и вторичных выводах. Например, при питании четырехполюсника со стороны первичных выводов (напряжение U1
) и холостом ходе на вторичных (напряжение ![]() , токи
, токи ![]() ,
, ![]() ) находим
) находим
![]() ;
; ![]() ,
,
а при коротком замыкании вторичных (напряжение ![]() , токи
, токи ![]() ,
, ![]() ),
),
![]() ;
; ![]() .
.
При работе четырехполюсника в цепи постоянного тока для вычисления коэффициентов достаточно измерить напряжения и токи.
Сопротивления холостого хода и короткого замыкания могут быть измерены теми же методами, что и любые другие сопротивления, например при помощи измерительного моста или амперметра, вольтметра, включенных только со стороны первичных или только со стороны вторичных выводов.
2. Практическая часть
2.1 Проектирование модуля
1. Проектируется схема для исследования соединения
2. Подбираются радиодетали, которые будут располагаться на будущей печатной плате модуля. Определяется подключение к исследуемой схеме измерительных приборов, источника сигнала.
3. Разрабатывается печатная плата.
2.2 Изготовление модуля
1. После разработки печатной платы, она выпиливается из фольгированного гетинакса.
2. В гетинаксе для последующей впайки радиодеталей сверлятся отверстия, На стороне, покрытой слоем металла, лаком наносятся дорожки. После этого плата вытравливается в растворе хлористого железа, лак удаляется и дорожки покрываются оловом.
3. На плату, в соответствии со схемой, монтируются резисторы, припаиваются провода
4. Изготавливается модуль для проведения работы.
5. Проверяется работоспособность модуля.
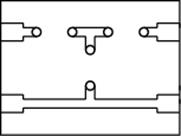
Рис. 2.1.
Номиналы резистивных элементов:
R1 = 3 кОм,
R2 = 3 кОм,
R3 = 15 кОм.
К входным выводам 1–1’ подключен источник питания, к выходным 2–2’ – нагрузка. Вольтметр V1 имеет возможность переключения с помощью тумблера S1 со входа схемы на выход и обратно (рис. 2).
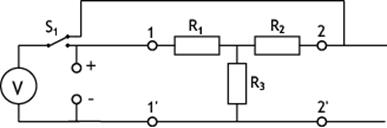
Рис. 2.2
Тумблеры S2 (S2.1 и S2.2 )и S3 (S3.1 и S3.2 ) переключают амперметр с измерения тока на входе схемы (рис. 3) на измерение тока на выходе (рис. 4) и обратно.

Рис. 2.3.
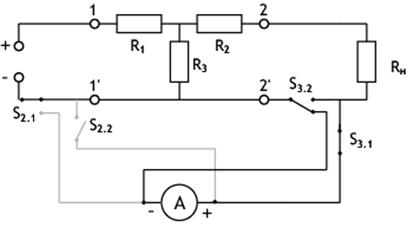
Рис. 2.4
Итоговая схема:
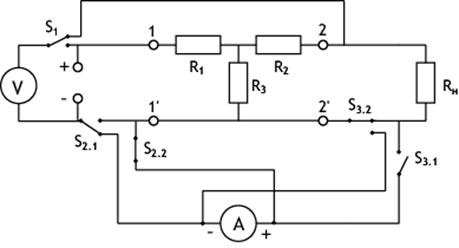
Рис. 2.5
Лабораторная работа
Изучение соединения типа «звезда»
1. Цель работы
Целью работы будет являться экспериментальное исследование соединения типа «звезда» при постоянном токе.
2. Задание для самостоятельной подготовки
2.1. По разделу 4 описания этой лабораторной работы следует ознакомиться с некоторыми пояснениями по лабораторной работе.
3. Методические указания по проведению работы
3.1. Включите стенд. Измерьте токи на резисторах R2 и R3 .
3.2. Найдите полное сопротивление цепи.
3.3. По закону Ома найдите ток I1 на резисторе R1 .
3.4. Применив первый закон Кирхгофа к точке А и второй закон к контуру ABCD, найдите токи на резисторах R2 и R3 .
3.5. Сравните найденные значения с полученными в ходе измерений.
4. Некоторые пояснения
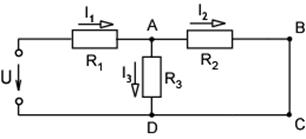
Схема цепи показана на рисунке. Напряжение питания U равно 10 В. Номиналы резисторов: R1 = R2 = 3 кОм, R3 = 15 кОм.
3. Расчетная часть

Схема цепи показана на рисунке.
Напряжение питания U = 10 В.
R1 = R2 = 3 кОм,
R3 = 15 кОм.
1. Расчет сопротивления цепи
Резистор R1 соединен последовательно с резисторами R2 и R3 . Следовательно, R пол = R 1 + R 23 .
Резисторы R2 и R3 соединены параллельно. Следовательно,
![]()
![]() и
и
![]() .
.
![]()
2. Расчет тока I1

3.
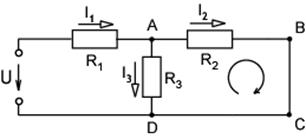
На основании первого закона Кирхгофа для узла А: ![]() .
.
Для контура ABCD по второму закону Кирхгофа:
![]() .
.
Имеем систему уравнений:
![]() ;
;
т. к. R3 = 5 R2
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
I2 =1,5 мА, I3 =0,3 мА.
Литература
1. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. – М.: Радио и связь, 2000
2. Зевеке Г.В., Ионкин П.А. Основы теории цепей. М.: ЭнергоАтомИздат, 1989
3. Дмитриева В.Ф., Прокофьев В.Л. Основы физики – М.: Высшая школа, 2003.