Реализация системы распространения ключей на основе алгоритма Диффи-Хеллмана длиной 256 бит
СОДЕРЖАНИЕ: Министерство образования и науки Российской Федерации Реализация системы распространения ключей на основе алгоритма Диффи-Хеллмана (длиной 256 бит)Министерство образования и науки Российской Федерации
Реализация системы распространения ключей на основе
алгоритма Диффи-Хеллмана
(длиной 256 бит)
Выполнил: Денисов А. П.
Проверил: Корниенко В. Т.
2010
Оглавление
Глава 1. Система открытого распределения ключей.. 4
1.1. История создания системы распределения ключей. 4
1.2. Система распределение ключей Диффи-Хеллмана. 6
1.3. Описание средств разработки. 7
Глава 2. Программная реализация открытого распространения ключей Диффи-Хеллмана. 9
2.1. Математические основы алгоритмов используемых в работе. 9
2.1.1. Сложение и вычитание. 9
2.1.2. Умножение «в столбик». 10
2.1.3. Возведение целого числа в квадрат. 12
2.1.4. Деление. Вычисление остатка. 13
2.1.5. Тест Рабина— Миллера. 16
2.1.6. Модульное возведение в степень. 18
2.1.7. Генерация простого числа. 20
2.1.8. Разложение числа на простые множители. 23
2.1.9. Нахождение первообразного корня. 24
3.1. Оценка стойкости алгоритма. 27
3.2. Оценка скорости работы алгоритма. 27
ВВЕДЕНИЕ
Проблема защиты информации путем ее преобразования, исключающего его прочтение посторонним лицом, волновала человеческий ум с давних времен. Актуальность этой проблемы не утратила своей остроты и в настоящее время, так как в эпоху массового применения компьютерных технологий задача защиты электронной информации приобрела характер широкомасштабной проблемы. Появление ассиметричных криптосистем произвели настоящий прорыв в современной криптографии и позволили передавать сообщения между абонентами без передачи секретного ключа.
Объектом исследования является алгоритм распределения ключей Диффи-Хеллмана.
Предмет исследования – программная реализация алгоритма распределения ключей Диффи-Хеллмана.
Цель работы - построение программного продукта на основе открытого распределения ключей Диффи-Хеллмана. Для ее решения были поставлены следующие задачи:
1. изучить криптографический алгоритм
2. построить математическую модель удобную для программирования
3. обосновать алгоритмическое решение программы
4. произвести оценку алгоритма
5. реализовать алгоритм криптосистемы на основе открытого распределения ключей Диффи-Хеллмана на одном из языков программирования
6. произвести проверку работоспособности и корректности работы программы
Глава 1 Система открытого распределения ключей .
1.1. История создания системы распределения ключей
В 1970 году Мартин Хеллман, молодой профессор, занимавшийся вопросами проектирования электрических систем в Стенфордском университете в Пало-Альто (шт. Калифорния). Хеллман увлекся проблемой в 1968 году, когда работал в IBM в Пенсильвании, [Завгородный В.И., 2001].
Хеллман рассказывает, что он прозрел после того, как прочитал статьи Клода Шенона по теории информации и криптографии, которые опубликовались в 1948 и 1949 годах. До этого я и представить себе не мог, насколько тесно связано шифрование и теория информации, - говорит он.
В статьях Шенона вопросы кодирования рассматривались в связи с задачей снижения электростатических помех, мешающих передаче радиосигналов. Шифрование, - заметил Хеллман, - решает диаметрально противоположную задачу. Вы вносите искажения при помощи ключа. Для того, кто слышит сигнал и не знает ключа, он будет выглядеть максимально искаженным. Но легитимный получатель, которому известен секретный ключ, может удалить эти помехи.
Пока Хеллман искал пути для решения проблемы, некий студент из MIT по имени Уайтфилд Диффи заинтересовался тем же самым. Но поиски Диффи начались значительно раньше. Я увлекся шифрованием, когда мне было всего десять лет, - вспоминает он. - У меня был учитель, который посвящал проблеме шифрования буквально целые дни. Я шел домой, а там меня ждали книги по этому предмету. Отец приносил мне их из библиотеки колледжа.
К 1973 году Диффи стал лаборантом и раздражал профессоров Стенфорда по искусственному интеллекту тем, что тратил все свое время и энергию на шифрование. Наконец, он оставил в покое своего учителя, взял отпуск и, одержимый своей идеей, отправился в путешествие по Восточному и Западному побережью, где встречался с экспертами по шифрованию и разыскивал редкие манускрипты.
А в это самое время Ральф Меркл, студент Университета Беркли (шт. Калифорния), занимающийся исключительно проектированием электрических систем, бродил по университетскому городку, снедаемый мыслями о шифровании, [Завгородный В.И., 2001].
Я думал о том, как обеспечить защиту коммуникаций между терминалом и компьютером, - рассказывает Меркл. - Я понял, что если оба, и терминал, и компьютер, используют случайные числа, восстановить ключ при передаче по открытым линиям связи будет невозможно.
Пытаясь объединить разрозненные идеи по шифрованию данных, Хеллман продолжал искать единомышленников. Однако получилось наоборот: в сентябре 1973 года его нашел Диффи. Их получасовая встреча плавно перешла в обед у Хеллмана, причем разговоры затянулись далеко за полночь.
Хеллман и Диффи начали работать над созданием алгоритма обеспечения защиты транзакций покупки и продажи, выполняемых с домашних терминалов. Я ломал голову над тем, как получить сообщение и преобразовать его таким образом, чтобы его воспринимали только те, кому предназначено, а посторонним информация была недоступна, - сказал Диффи. - Затем я понял, что при помощи сертификатов и подписи можно создать сообщение, которое сможет прочитать только один человек, [Завгородный В.И., 2001].
Хеллман и Диффи сообщили, что их первая статья по теории цифровых подписей вышла в декабре 1975 года. Представлена она была полгода спустя на Национальной компьютерной конференции в Нью-Йорке.
Оставаясь невидимым для конечных пользователей, открытый ключ использует открытый и секретный ключи для шифрования и дешифрования сообщений вместе с цифровыми подписями, а также для проверки личности отправителя. В его основе лежат довольно сложные математические преобразования.
После Беркли в 1975 году Меркл сформулировал задачу защиты коммуникаций, несвязанную с подписью и сертификатом. Он взялся за решение проблемы распространения открытого ключа, исходя из предпосылки применения смешения случайных чисел. Прочитав статью Хеллмана-Диффи, Меркл встретился с первым, который уговорил Меркла перенести свою аспирантскую работу в Стенфорд.
В 1976 г. Мерклу удалось при помощи Хеллмана и Диффи справиться с задачей распространения открытого ключа и развить аппарат цифровой подписи. Они создали и запатентовали систему, получившую имя Диффи-Хеллмана. Открытие обеспечило нашему трио внимание со стороны средств массовой информации.
Но внимание это улетучилось так же быстро, как и возникло. Изобретатели опередили свое время: задача, решение которой они предлагали, еще не была сформулирована, [Завгородный В.И., 2001].
1.2. Система распределение ключей Диффи-Хеллмана
Зарождение двухключевой криптографии и основные криптосистемы с открытым ключом связаны с использованием функции возведения в большую дискретную степень по модулю большого простого числа
f( x) = x ( mod p),
где х — целое число. 1 x р—1, р — k-битовое простое число, - первообразный корень по модулю р, [Молдовян Н.А. и др., 2004].
Используя данную функцию, учеными Диффи и Хеллманом была показана возможность построения практически стойких секретных систем, которые не требуют передачи секретного ключа. Предложенная ими система получила название метода открытого распространения ключей. В ней каждый абонент выбирает случайным образом секретный ключ х и вырабатывает открытый ключ у соответствующий выбранному секретному ключу, в соответствии с формулой
у = х ( mod p).
Системой Диффи-Хеллмана называется следующий способ использования дискретного возведения в степень для обмена секретными ключами между пользователями сети с применением только открытых сообщений. Выбирается большое простое число р и соответствующий ему первообразный корень а р. Для обеспечения стойкости рассматриваемой системы открытого шифрования на число р накладывается следующее условие: разложение числа р-1 на множители должно содержать, по крайней мере, один большой простой множитель; размер числа р должен быть не менее 512 бит.
Механизм распределения секретных ключей по открытому каналу состоит в следующем. Каждый абонент выбирает случайный секретный ключ x и вырабатывает открытый ключ у, соответствующий выбранному секретному ключу, в соответствии с формулой
y = x (mod p).
Два абонента А и В могут установить секретную связь без передачи секретного ключа следующим образом. Абонент А берет из справочника открытый ключ у B абонента В и, используя свой секретный ключ хА , вычисляет общий секретный ключ:
Аналогично поступает абонент В:
Таким образом, оба абонента сформировали одинаковый секретный ключ ZAB
без использования какого-либо заранее оговоренного общего секрета. Владея только им известным секретом и используя его в качестве мастер-ключа, данная пара абонентов может зашифровывать направляемые друг другу сообщения. Указанные выше вычисления легко осуществимы для достаточно больших значений р, а, у
и х
(например, имеющих в двоичном представлении длину 4096 бит и более). Атакующему известны значения 
и 
,
но для того чтобы вычислить ZAB
, он должен решить задачу дискретного логарифмирования и определить либо х
A
, либо х
B
.
Легко найти большие значения р
(более 1024 бит), для которых задача дискретного логарифмирования является трудно решаемой. Если будут найдены вычислительно эффективные методы решения задачи дискретного логарифмирования, то метод Диффи-Хеллмана окажется несостоятельным — в связи с этим говорят, что данный .метод открытого распределения ключей основан на сложности дискретного логарифмирования. В настоящее время в общем случае задача дискретного логарифмирования практически неразрешима, что дает возможность широкого практического применения метода Диффи-Хеллмана и многочисленных систем ЭЦП, основанных на сложности вычисления дискретных логарифмов.
Не следует упускать из виду проблему аутентификации открытых ключей. Корректность протоколов с использованием асимметричных шифров может быть обеспечена только в случае, если все открытые ключи в справочнике открытых ключей являются подлинными. Если открытый ключ какого-либо абонента нарушителю удастся подменить, то секретные сообщения, посланные данному абоненту, будут доступны нарушителю. Таким образом, двухключевые шифры обеспечивают решение проблемы распределения секретных ключей, однако проблема аутентификации сохраняется и имеет фундаментальный характер, хотя требование подтверждения подлинности (аутентификации) относится уже к открытому, а не к секретному ключу. В неявном виде аутентификация открытого ключа включает в себя аутентификацию секретного ключа, [Молдовян Н.А. и др., 2004].
1.3. Описание средств разработки.
Проект реализован с помощью среды C++Builder 6, которая позволяет разрабатывать серверы и клиенты Web-служб. C++Builder 6 обеспечивает поддержку клиентов Web-служб, использующих как SOAP encoding, так и Document Literal style. Document Literal style используется в Microsoft. Net Web Services. Предоставляя набор выскокоуровненвых компонент и визардов, включая автоматическую публикацию WSDL-описателей Web-служб в run-time и генерацию кода на основе WSDL (WSDL Importer), C++Builder 6 позволяет разработчикам легко адаптировать существующие приложения для работы в режиме Web-служб и доступа к ним как во внутрикорпоративной сети, так и через Web.
C++ Builder позволяет задействовать ранее созданный исходный код на C и С++. Можно работать с унаследованными проектами и приложениями третьих фирм на Borland C++ и Visual C++ внутри интегрированной среды разработки C++ Builder. Расширенная совместимость с исходным кодом MS Visual C++, включая поддержку исходных текстов MSDN и SDK, позволяет использовать новейшие версии библиотек MFC и ATL. За счет поддержки стандарта C++, RTTI, библиотек STL, RTL, ATL и MFC, позволяет компилировать и собирать проекты, созданные ранее на отличных от C++ Builder средствах разработки для C/C++.
Глава 2. Программная реализация открытого
распространения ключей Диффи-Хеллмана.
2.1. Математические основы алгоритмов используемых в работе
При создании программы возник вопрос: каким образом представлять большие числа? Решение было принято о том что число можно занести в массив типа unsigned char в который помещается два шестнадцатеричных числа, которые обрабатываются как 256-разрядные:
Это позволяет значительно упростить функции.
Размещение значений в массиве обратное, т.е. число “FF AB C4” в массиве будет представлено как: unsigned char a[3]={0xC4, 0xAB, 0xFF};
Все функции в программе предназначены для работы с 256-битными значениями.
Алгоритмы арифметики целых чисел и полиномов во многом похожи, поскольку представление целого числа а в системе счисления с основанием B в виде:
где 0 ai
В, аналогично представлению полинома 
.
Ниже описаны алгоритмы, используемые в программном продукте. Алгоритм представлен по следующей структуре: теоретические основы и листинг программы.
2.1.1. Сложение и вычитание
Операции сложения и вычитания для чисел и полиномов выполняются практически одинаково. Отличие заключается в том, что при сложении (вычитании) чисел возникает перенос в следующий разряд, а при операциях над полиномами перенос отсутствует.
Пусть неотрицательные целые числа а и b заданы в системе счисления с основанием В:
где 0 ai ; bi B. Для удобства считаем, что оба числа имеют равную длину, при необходимости старшие разряды меньшего числа заполняем нулями.
Сложение выполняется «в столбик».
Алгоритм 1 . Сложение целых чисел, [Молдовян Н.А. и др., 2004].
Вход.
Целые числа 
, 
.
Выход.
Сумма 
.
1. Положить 
2. Для i = 0, 1,...,п- 1 выполнить следующие действия.
2.1. Вычислить 
2.2. Положить 
,
.
3. Положить сп = s.
4. Результат: 
.
Переменная s
означает перенос в старший разряд и всегда принимает значение 0
(при ai
+bi
+s B) или 1 (при ai
+bi
+s B). На шаге 2.1 Может произойти не более одного переноса. Действительно:
ai +bi +1 (B-1)+(B-1)+1 2B-12B.
Вычитание аналогично сложению изменение только в шаге 2.1. 
.
В этом случае если t отрицательное то у следующего элемента занимается 1.
Сложность алгоритма сложения и вычитания равна О(п).
Код функции summa(сумма) :
for (i=0;i=32;i++){
s=a[i]+b[i]+buf; //Общее значение
c[i]=s;//число заносимое в ячейку
buf=(s)8;//остаток
}
Код функции sub(разность) c = a-b :
for(i=0;i=31;i++){
s=a[i]-b[i]+buf;
buf=s8;
c[i]=s;
}
2.1.2. Умножение «в столбик».
Операция умножения является одной из наиболее трудоемких и вместе с функцией деления определяет время работы алгоритма.
Пусть неотрицательные целые числа а и b заданы в системе счисления с основанием B.
где 0 ai B, 0 bi B
Самый очевидный способ умножения — умножение «в столбик».
Алгоритм 2 . Умножение целых чисел «в столбик», [Молдовян Н.А. и др., 2004].
Вход.
Целые числа
, 
где 0 b a.
Выход.
Произведение
1. Для i = 0, 1,...,п- 1 положить ci = 0
2. Для i = 0, 1,...,п- 1 выполнить следующие действия.
2.1. Для j = 0, 1,...,п- 1:
2.1.1. Положить s= 0.
2.1.2. Вычислить t = ci+j
+ai
bj
+s , ci+j
=t (mod B) , 
.
2.2. Положить ci + n =s.
3. Результат: 
Во внешнем цикле этого алгоритма вычисляются частичные произведения 
,
а во внутреннем — произведения 
, где j = 0, 1, ..., п-
1. Текущий разряд произведения равен t (mod В), а очередной перенос: . При этом на шаге 2.1.2 выполняется неравенство:
Сложность умножения в «столбик» О( n2 ).
Функция умножения реализована как умножение с вычислением модуля.
Код функции mult_mod (умножение по модулю) c=a*b (mod mod):
void mult_mod(unsigned char a[33],unsigned char b[33],unsigned char c[33]){
int i,j,k,s,t;
unsigned char d[65]={0};
for (k=0;k=31;k++) c[k]=0; //очищение переменной
for(i=0;i=31;i++){
s=0;
for(j=0;j=31;j++){
t=d[i+j]+a[i]*b[j]+s;
d[i+j]=t;
s=t8;
}
d[i+32]=s;
}
modul(d,mod,c); //вычисление модуля mod - глобальная переменная
}
2.1.3. Возведение целого числа в квадрат.
Отдельно реализована функция возведения в квадрат.
Алгоритм 3 . Возведение в квадрат, [Молдовян Н.А. и др., 2004].
Вход
. Целое положительное число .
Выход
. Значение 
1. Для i = 0, 1,...,п- 1 положить сi = 0.
2. Для i = 0, 1,...,п- 1 выполнить следующие действия.
2.1. Положить 
, 
, .
2.2. Для j = 0, 1,...,п-
1 вычислить t = ci
+
j
+ai
aj
+s , ci
+
j
=t (mod B) , 
.
2.3. Положить ci + n =s.
Результат: с .
На шаге 2.2 алгоритма выполняется неравенство:
Это означает что t может занимать более двух разрядов в системе исчисления B.
Сложность алгоритма возведение в квадрат О(
).
Код функции step2 (возведение в квадрат) b=a^2 (mod mod):
void step2(unsigned char a[33],unsigned char b[33]){
unsigned char c[65]={0};
int t,s,i,j;
for(i=0;i=32;i++){
t=c[2*i]+a[i]*a[i];
c[2*i]=t%256;
s=t8;
for(j=i+1;j=32;j++){
t=c[i+j]+2*a[i]*a[j]+s;
c[i+j]=t%256;
s=t8;
}
c[i+33]=s;
}
modul(c,mod,b);//вычисление модуля
}
2.1.4. Деление. Вычисление остатка.
Для деления в общем случае используется алгоритм Д. Кнута . Будем делить «в столбик» число 
на число . Найдем такое частное 
и остаток
,
что
.
При делении на каждом шаге находим частное 
от деления некоторого (n+1)-разрядного числа 
на b,
где О R/bВ
. Неравенство R/b В
эквивалентно неравенству R/Bb,
откуда b
:
Полагая R = R - Qb, получаем 0 R b.
Для определения числа Q будем использовать аппроксимацию
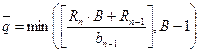[1]
При 
получаем 
,
то есть определение наименьшего из двух чисел в выражении
(1) сводится к проверке равенства .
Теорема 1.
Пусть , , если 
то значение 
удовлетворяет неравенству 
, где q
определяется из соотношения (1.1).
Алгоритм деления с остатком. Чтобы старший разряд делителя удовлетворял условию теоремы 1.1, числа а и
b
нужно умножить на некоторое целое число d0, такое что 
где.
, 
Частное при этом не изменяется: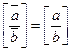 
. Число разрядов 
недолжно превышать число разрядов b, число разрядов в 
может быть на единицу больше, чем в а
(если это не так, полагаем ат+п
= 0).Выбираем d
равным степени двойки, так как умножение на d
в этом случае выполняется сдвигом.
Алгоритм 4 . Деление «в столбик», [Молдовян Н.А. и др., 2004].
Вход.
Неотрицательные целые числа 
, 
;
Выход.
Целые числа ,
,
такие, что
, 
.
1. Определить такое целое число d0, что 
, где 
2. Положить 
.
3. Для i = m + n , m + n - 1, ..., n выполнить следующие действия
3.1. Если ri
=bn
-1
, то положить
; в противном случае найти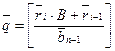 
где 
.
3.2. Пока 
полагать 
3.3. При 
положить .
3.4. Вычислить 
и 
.
4. Результат: 
,
Сложность алгоритма деления «в столбик» равна О(mn).
Реализованы две функции целочисленное деление и вычисление остатка.
Основной код функций:
for(i=64;i=0;i--){
ai=i+1;
if(a[i]!=0)break;
}
for(i=32;i=0;i--){
n=i+1;
if(b[i]!=0)break;
}
m=ai-n;
//printf(b = %x ,b[n-1]);
d=1;
if(b[n-1]128){
for(i=2;i=7;i++){
d*=2;
if((b[n-1]*d)=128) break;
}
}//оценить d шаг 1
mult(b,d,bt);//шаг 1 b~=b*d
for(i=0;i=63;i++){r[i]=a[i];}//шаг 2
for(i=m+n;i=n;i--){//шаг 3
s=0;
for(k=i-n;k=i;k++){
t=r[k]*d+s;
rt[k]=t;
s=t8;
}// шаг 3.1 r~=r*d
if(rt[i]==bt[n-1]) qt=255;
else qt=((rt[i]*256+rt[i-1])/bt[n-1]);// шаг 3.1 r~=r*d
while((bt[n-2]*qt)((rt[i]*256+rt[i-1]-qt*bt[n-1])*256+rt[i-2])){
qt-=1;
}// шаг 3.2
mult(b,qt,bqt);
for(k=i;k=i-n;k--){
if(r[k]bqt[k-m]){
qt-=1;
break;
}
if(rt[k]bqt[k-m])break;
}// шаг 3.3
mult(b,qt,bqt);
s=0;
for(k=i-n;k=i;k++){
t=r[k]-bqt[k-m]+s;
r[k]=t;
s=t8;
}
c[i-n]=qt;
m-=1;
}
В итоге: r - остаток от деления ,c – целое от деления.
2.1.5. Тест Рабина —Миллера
На сегодняшний день для проверки чисел на простоту чаще всего используется тест Рабина-Миллера, основанный на следующем наблюдении. Пусть число п
нечетное и 
, где r
— нечетное. Если п
простое, то для любого а 2,
взаимно простого с п,
выполняется условие теоремы Ферма (а
r
= 1 (mod n
)). Разложим число 
на множители:
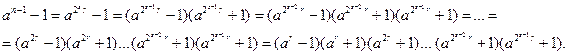
Тогда в последнем произведении хотя бы одна из скобок делится на п,
то есть либо а
r
=
1(mod п),
либо среди чисел а , а
r
, ..., 
найдется сравнимое с -1 по модулю п.
Обращение этого свойства лежит в основе теста Рабина-Миллера.
Алгоритм 5 . Тест Рабина-Миллера, [Молдовян Н.А. и др., 2004].
Вход. Нечетное целое число п 5.
Выход. «Число п, вероятно, простое» шли «Число п составное».
1. Представить п -
1 в виде ,
где число r
нечетное.
2. Выбрать случайное целое число а, 2 а п - 2.
3. Вычислить 
.
4. При 
и 
выполнить следующие действия.
4.1. Положить j = 1.
4.2. Если j s – 1 и .
4.2.1. Положить y= y2 (mod n )
4.2.2. При у = 1 результат: «Числю п составное».
4.2.3. Положить j=j+1.
4.3. При 
результат: «Число п
составное».
5. Результат: «Число п, вероятно, простое».
В результате выполнения теста для простого числа п
в последовательности a
(mod n),
a2
r
(
mod
n),
..., (mod n)
обязательно перед 1 должна появиться -1 (или, что то же самое, п
-
1 (mod n)).
Это означает, что для простого числа п
единственными решениями сравнения y2
= 1 (mod n
) являются у = ±1 (mod n). Если число n
составное и имеет k
1 различных простых делителей (то есть не является степенью простого числа), то по китайской теореме об остатках существует 2
k
решений сравнения у2
=
1 (mod n).
Действительно, для любого простого делителя pi
числа п
существует два решения указанного сравнения: у = ±
1 (mod р
i
).
Поэтому k
таких сравнений дают 2
k
наборов решений по модулям pi
,
содержащих элементы ± 1.
Сложность алгоритма равна 
Код функции rabin (поверка на простоту):
/*mod – проверяемое значение,
st – степень числа при передаче в функцию sstep();
osn – основание при вычислении
Пр: osnst (mod mod)
*/
int rabin(){
unsigned char c[33]={0};
int i,k,g,t,q,r,x,j,fl,w;
unsigned char d[33]={0};//для р.м. р-1
srand(time(0));
for(i=0;i=31;i++) st[i]=mod[i];
st[0]-=1;
for(i=0;i=31;i++){
d[i]=st[i];
}
for(i=0;;i++){
q=i+1;
r=0;
for(k=31;k=0;k--){
t=st[k]+(r8);
st[k]=(t1);
r=t%2;
}
if(int(st[0])%2==1) break;
}//находим n-1=(2^s)*q где n-простое
for(i=0;i=6;i++){
osn[i]=rand();
}//генерируем основание
step(c);
x=comp_sp(c,d);
if(x==2){
return 1;
}
x=rav(c);
if(x==0) return 1;
j=1;
while(j=q-1){
step2(c,c);
x=rav(c);
if(x==0) return 0;
j++;
}
x=comp_sp(c,d);
if(x!=2){
return 0;
}
return 1;
}
2.1.6. Модульное возведение в степень
При обычном рекурсивном способе: a0
=1,
a
n
=(
a
n-1
)
a (
mod
n).
Требуется n-1 операций возведения в степень по модулю т,
то есть O(
m2
)
операций модульного умножения. Если же предварительно представить показатель п
в двоичном виде 
где к
= [log2
n], и, 
, то
где 
. При таком способе вычисления потребуется k модульных возведений в квадрат и 
модульных умножений. Учитывая, что каждый разряд принимает значение 0 или 1 равновероятно, можно считать, в среднем требуется 1,5 log m
модульных умножений.
Алгоритм 6 Модульное возведение в степень, [Молдовян Н.А. и др., 2004].
Вход.
Целое число а,
1 а т;
показатель степени п 2,
Выход. с = ап (mod т).
1. Положить 
.
2. Для i = k-1 , k-2 , … , 0 выполнить следующие действия.
2.1. Вычислить 
2.2. При ni
= 1 вычислить 
.
3. Результат: с.
Код функции step (степень):
osn, st, mod – глобальные переменные основание, степень, модуль соответственно.
с = osnst (mod mod)
void step(unsigned char c[33]){
int i,k,t,r;
int pole[256]={0};
unsigned char d[33]={0};
for(i=0;i=31;i++){
union{unsigned char pol;
struct{unsigned b0:1;
unsigned b1:1;
unsigned b2:1;
unsigned b3:1;
unsigned b4:1;
unsigned b5:1;
unsigned b6:1;
unsigned b7:1;
}bit;
}cod;
cod.pol=st[i];
pole[i*8+0]=cod.bit.b0;
pole[i*8+1]=cod.bit.b1;
pole[i*8+2]=cod.bit.b2;
pole[i*8+3]=cod.bit.b3;
pole[i*8+4]=cod.bit.b4;
pole[i*8+5]=cod.bit.b5;
pole[i*8+6]=cod.bit.b6;
pole[i*8+7]=cod.bit.b7;
}//Представление числа в битовом формате
for(k=255;k=0;k--){
r=k;
if(int(pole[k])==1)break;
}
if ( int(pole[r])==0) c[0]=1;
else
for(i=0;i=31;i++){
c[i]=osn[i];
}
for(k=r-1;k=0;k--){
step2(c,d);
for(t=31;t=0;t--) c[t]=d[t];
if(int(pole[k])==1){
mult_mod(c,osn,d);
for(t=31;t=0;t--) c[t]=d[t];
}
}
}
2.1.7. Генерация простого числа
Существуют различные алгоритмы генерации простых чисел. Многие из них вырабатывают числа, обладающие специальными свойствами. Рассмотрим способ генерации, использующий вероятностные алгоритмы проверки чисел на простоту.
Алгоритм 7 Генерация простого числа, [Молдовян Н.А. и др., 2004].
Вход. Разрядность к искомого числа р ; параметр t 1
Выход.
Число р,
простое с вероятностью не менее 
1. Сгенерировать случайное k-битное число 
2. Положить bk =1 , b0 =1
3. Проверить, что р не делится на простые числа 3, 5, 7, ...,251 .
4. Для i = 1,2, ..., t выполнить следующие действия.
4.1. Выбрать случайное число а, 2 а р - 2.
4.2. Проверить число р тестом Миллера-Рабина для основания а. Если число р не прошло тест, то p = p+2 и вернуться на шаг 3.
5. Результат: p.
Равенство bk =1 на шаге 2 гарантирует, что длина числа p в точности равна к бит, равенство b0 =1 обеспечивает нечетность числа p.
Код функции random (генерация простого числа):
void random(unsigned char c[33]){
unsigned int prost[54]={2,3,5,7,…, 241,251};
unsigned char copy_mod[33]={0};
int w,x,i,k,t,s,f,g=2,r,z,flag=0;
srand(time(0));
for(i=0;i=31;i++){
mod[i]=rand();
}//генерация простого числа
mod[0]|=1;
mod[31]|=128; //не четное и 256 бит
st[0]=mod[0]-1;
for(k=1;k=31;k++){
st[k]=mod[k];
}//st= простое-1
for(w=0;;w++){
for(r=0;r=31;r++){
copy_mod[r]=mod[r];
mod2[r]=mod[r];
}
flag=0;
for(i=0;i=53;i++){
r=0;
for(k=31;k=0;k--){
t=mod[k]+(r8);
r=t%prost[i];
}//проверка на делимость на маленькие простые числа
if(r==0){//число составное
flag=1;
break;
}
}
if(flag==0){
x=rabin();//проверка на простоту
if(x==1){
for(k=0;k=6;k++){//еще 7 проверок на простоту
st[0]=mod[0]-1;
for(f=1;f=31;f++){
st[f]=mod[f];
}
x=rabin();
if(x==0)break;//ели не прошло тест
}
if(x!=0){
x=razlogenie();//если простое
// нахождение первообр. корня
if(x==1)break;//если число разложено
//на простые и найден первообр. корень
}
}
for(r=0;r=31;r++)mod[r]=copy_mod[r];
}
s=0;
g=2;
for(k=0;k=31;k++){//прибавить к проверяемому 2
t=mod[k]+g+s;
g=0;
s=t8;
mod[k]=t;
if(s==0)break;
}
mod[0]|=1;
mod[31]|=128;
for(k=0;k=31;k++){st[k]=mod[k];}
st[0]-=1;
}
}
2.1.8. Разложение числа на простые множители.
В ходе реализации понадобилось разложить большое число на простые множители один из которых является большим.
Алгоритм 8 Разложение числа на простые множители, [Молдовян Н.А. и др., 2004].
Вход. Раскладываемое число n.
Выход. Число не раскладывается на простые множители (с большим простым множителем); число раскладывается на q1 , q2 ,…, qk - различных простых делителя.
1. Создание ряда простых чисел p1 =2 ,p2 = 3,…, p844 = 6491;
2. Положить t = 0.
3. Для i = 1,2, ..., 844 выполнить следующие действия.
3.1. Если w=n/pi целое, t = t + 1, qt = pi ;
3.1. Пока w=n/pi целое, n=n/pi .
4. Проверить число n тестом Миллера-Рабина.
Код функции разложение razlogenie()
int razlogenie(){
int i,r,k,t,x,w,fl=0,counter=0;;
unsigned char p[33]={0};
int mass[300]={0};
unsigned char c[33]={0};
unsigned int prost[6900]={2,3,5,7,…,69491,69493};
for(k=0;k=32;k++) p[k]=mod[k];
p[0]-=1;
for(i=0;i=6860;i++){
r=0;
for(k=31;k=0;k--){
t=p[k]+(r8);
c[k]=t/prost[i];
r=t%prost[i];
}
for(k=0;k=31;k++) p[k]=c[k];
if(r==0){
for(k=0;k=31;k++) mod[k]=p[k];
if(fl!=i){
fl=i;
mass[counter]=prost[i];
counter++;
}
i--;
}
if(r!=0){
for(k=0;k=31;k++) p[k]=mod[k];
}
}
x=rabin();
if(x==1){
pervoobr(mass);//вычисление первообразного корня
}
return x;
}
2.1.9. Нахождение первообразного корня.
Утверждение
Пусть q1
,
q2
,…,
qk
-
различные простые делители функции Эйлера 
от числа п.
Для того чтобы число g, взаимно простое с п,
было первообразным корнем по модулю п,
необходимо и достаточно, чтобы это g
не удовлетворяло ни одному из сравнений:
,
,…,
.
Алгоритм 9 Нахождение первообразного корня, [Молдовян Н.А. и др., 2004].
Вход.
Простое число n, q1
,
q2
,…,
qk
-
различные простые делители функции Эйлера 
Выход. Первообразный корень g.
1. Генерация числа 1 g n.
2. Для i = 1,2, ..., k выполнить следующие действия.
2.1. Если 
перейти к шагу 1.
3. Число g первообразный корень по модулю n.
Код функции pervoobr (нахождение первообразного корня):
void pervoobr(int mass[300]){
unsigned char g[33]={0};
unsigned char c[33]={0};
unsigned char b[33]={0};
int i,k,t,x,flag;
srand(time(0));
for(i=0;i=31;i++){
g[i]=mod[i];
mod[i]=mod2[i];
osn[i]=0;
}
for(k=0;k=1000;k++){
flag=2;
for(i=0;i=28;i++) osn[i]=rand();
del(mod,g,st);
step(c);
x=rav(c);
if(x!=0){
flag=1;
for(i=0;i=31;i++){
c[i]=0;
for(i=0;i=300;i++){
if(mass[i]!=0){
c[0]=mass[i];
c[1]=(mass[i]8);
del(mod,c,b);
for(t=0;t=31;t++)st[t]=b[t];
step(b);
x=rav(b);
if(x==0) flag=0;
}
}
}
}
if(flag==1){
break;
}
}
}
Глава 3. Оценка алгоритма.
3.1. Оценка криптостойкости алгоритма
Протокол обмена ключами Диффи–Хеллмана не обеспечивает аутентичности согласованного ключа. Активный противник, внедренный в канал связи между двумя пользователями А и Б, может манипулировать сообщениями протокола и начать атаку “человек посередине” (man-in-the-middle attack).
В ходе этой атаки Злоумышленник перехватывает и блокирует первое сообщение от А к Б, т. е. число gа , маскируется под А и посылает Б следующее сообщение.
Злоумышленник (под именем А) — Б: gm = gm (mod p).
Б , следуя инструкциям протокола, возвращает Злоумышленнику (под именем А) число gb . Это число снова перехватывается и блокируется Злоумышленником. Теперь Злоумышленник и Б согласовали между собой ключ gb m =(mod p) , хотя Б считает , что он разделил этот ключ с А.
Аналогично Злоумышленник, имитируя Б, может согласовать другой ключ с А (т.е. число ga m (mod p)). Впоследствии Злоумышленник может использовать оба ключа для чтения и подмены “секретных” сообщений, которыми обмениваются А и Б, или поочередно имитировать этих пользователей.
Атака на протокол обмена ключами Диффи–Хеллмана вполне реальна, поскольку этот протокол не предусматривает проверки аутентичности источника сообщений. Для того чтобы ключи были согласованы только между А и Б, обе стороны должны быть уверены друг в друге.
Минусы программной реализации, снижающие стойкость:
-при вычислении функции step(), описанной выше, появляется прямая зависимость времени вычисления от количества единиц (при бинарном представлении) в степени. Что может дать представление о количестве единиц в секретном ключе.
- в программном продукте не реализована полная очистка оперативной памяти.
- секретные ключи хранятся в открытом виде на диске.
- не реализована возможность вычисления хэш, в результате чего возможна модификация ключей.
3.2. Оценка скорости работы алгоритма
Оценка производилась на компьютере:
Тип ЦП AMD Sempron, 1666 MHz ,2400+
Чипсет системной платы nVIDIA nForce2 Ultra 400
Системная память 1024 Мб (DDR SDRAM)
Наиболее долгой является операция генерации большого простого числа p , такого что p-1 раскладывается на простые множители, причем разложение должно иметь один большой простой множитель, и нахождение первообразного корня. Этот процесс является вероятностным и может привести к неопределенной отсрочке.
Результаты тестирования программы приведены в таблице 1.
Таблица 1.
Тест на время реализации базовых операций программного продукта
| Время генерации, сек. |
Количество проверенных значений, ед. |
Скорость проверки значений, ед./сек. |
| 16 |
2700 |
168,8 |
| 34 |
7400 |
217,6 |
| 26 |
4400 |
169,2 |
| 160 |
23300 |
145,6 |
| 48 |
10000 |
208,3 |
| 83 |
17600 |
212,0 |
| 4 |
400 |
100,0 |
| 137 |
23900 |
174,5 |
| 5 |
600 |
120,0 |
| Среднее значение: |
168,5 |
Основная нагрузка для проверки скорости работы лежит на функции вычисления степени по модулю. Скорость работы алгоритма зависит от выбранной степени, чем больше единиц в бинарном представлении степени, тем дольше будет происходить операция возведения в степень по модулю.
З аключение
В ходе курсовой работы был изучен алгоритм распределения ключей Диффи-Хеллмана и реализован на языке программирования С++. Полученный программный продукт отвечает требованиям, предъявляемым к системе открытого распространения ключей Диффи-Хеллмана.
У программного продукта есть недостатки:
-при вычислении функции step( ), описанной выше, появляется прямая зависимость времени вычисления от количества единиц (при бинарном представлении) в степени. Что может дать представление о количестве единиц в секретном ключе.
- в программном продукте не реализована полная очистка оперативной памяти.
- секретные ключи хранятся в открытом виде на диске.
- не реализована возможность вычисления хэш, в результате чего возможна модификация ключей.
- не реализована аппаратная система.
Таким образом, поставленная в работе цель была выполнена, решены необходимые задачи и на основании их сделаны соответствующие выводы.
Литература
- Аграновский А.В., Хади Р.А. Практическая криптография. Алгоритмы и их программирование. М.: Солон-Пресс, 2002 г. – 256 с.
- Галуев Г.А. Математические основы криптологии. Учебно-методическое пособие. Таганрог, 2003 г. 79 с.
- Дебора Керр Computerworld #39/1996 Тайна открытого ключа. http://www.osp.ru/cw/1996/39
- Завгородний В. И. Комплексная защита информации в компьютерных системах. М.: Логос, 2001 г. – 264 с.
- Кнут Д.Э. Искусство программирования. Т. 2. Получисленные алгоритмы. М. СПб. – Киев: Вильямс, 2000 г. – 832 с.
- Молдовян Н. А., Молдовян А. А., Еремеев М. А.. Криптография. От примитивов к синтезу алгоритмов. С-Пб.: БХВ-Петербург, 2004 г. – 505 с.
- Маховенко Е. Б. Теоретико-числовые методы в криптографии. М.: Гелиос АРВ, 2006 г. – 320 с.
- Нильс Фюргесон, Брюс Шнайер. Практическая криптография. Киев: Диалектика, 2004 г. – 432 с.
- Рябко Б. Я., Фионов А. Н. Криптографические методы защиты информации. Учебное пособие. М.: Горячая линия – Телеком, 2005 г. – 232 с.
- Смарт Н. Криптография. М.: Техносфера, 2006 г. – 528 с.
- Шнайер Б.. Прикладная криптография. Протоколы, алгоритмы и исходные тексты на языке С. М.: Триумф, 2002 г. – 816 с.