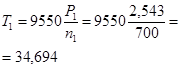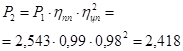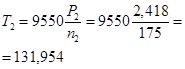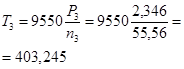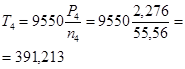Редуктор двухступенчатый
СОДЕРЖАНИЕ: Омский государственный технический университет Кафедра «Детали машин» Редуктор двухступенчатый Пояснительная записка 2005 г. Содержание Задание на курсовой проектОмский государственный технический университет
Кафедра «Детали машин»
Редуктор двухступенчатый
Пояснительная записка
2005 г.
Содержание
Задание на курсовой проект
Введение
1. Предварительный расчёт привода
1.1 Определение недостающих геометрических размеров И.М
1.2 Определение потребной мощности и выбор электродвигателя
1.3 Разбивка общего передаточного числа редуктора по ступеням передач
1.4 Составление таблицы исходных данных
2. Проектирование редуктора
2.1 Расчёт первой ступени редуктора
2.2 Расчёт второй ступени редуктора
2.3 Расчёт валов редуктора
2.3.1 Проверка сечений валов
2.3.2 Расчет валов редуктора на статическую прочность
2.3.3 Расчёт тихоходного вала на сопротивление усталости
2.3.4 Расчет тихоходного вала на жесткость
2.4 Расчет подшипников редуктора
2.5 Расчет шпоночных соединений
3. Эскизное проектирование
3.1 Проектные расчёты валов
3.2 Определение расстояние между деталями передач
3.3 Выбор типа и схемы установки подшипников
4. Выбор посадок
5. Выполнение рабочих чертежей деталей
6. Выбор смазки
Заключение
Литература
Задание на курсовой проект
Шифр КП.15.Д1.6.1.9
Студенту факультет гр.
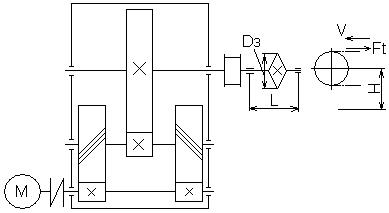
Спроектировать редуктор ленточного конвейера
Кинематическая схема График нагрузки
 |
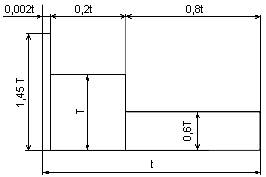
Срок службы – 5 лет
![]()
Исходные данные
1. Окружное усилие на звёздочке – Ft, кН 3,5
2.Скорость цепи конвейера – V, м/с 0,65
3.Шаг цепи по ГОСТ 588-81- Р, мм 100
4.Число зубьев ведущей звёздочки- Z 7
5.Высота установки ведущего вала – Н, мм 350
6.Установочный размер И.М.- L, мм 400
Разработать
1.Сборочный чертёж редуктора 27.04.05
2.Рабочие чертежи деталей 11.05.05
Задание получил 9.02.05. разработчик
Введение
В данной работе произведена разработка конструкции цилиндрического двухступенчатого редуктора. Выполнен расчет и проверка основных его элементов: зубчатых передач, валов, подшипников, шпоночных соединений. Расчет производился на основании критериев, обеспечивающих надёжность данного устройства на всех этапах эксплуатации.
На первом этапе расчетов были определены необходимые параметры привода (частота вращения двигателя, моменты на валах, передаточное отношение редуктора). Далее, на этапе расчета передач, были найдены допускаемые напряжения, геометрические и кинематические параметры передач и произведена их проверка на выносливость и прочность. Все валы рассчитаны на статическую прочность, а тихоходный вал проверен на сопротивление усталости и на жесткость. Далее производится проверка подшипников выбранной серии. Затем следует проверка шпонок и выбор смазки. В конце дается обоснование выбора посадок и сведения по выполнению рабочих чертежей.
Данный редуктор может применяться в различных отраслях промышленности.
Техническая характеристика редуктора: мощность на входном валу – 3 кВт; частота вращения быстроходного вала – 700 об/мин; общее передаточное число редуктора – 12,6; крутящий момент на выходном валу – 403,2 Нм.
Работа выполнена на основании задания на курсовой проект.
1. Предварительный расчёт привода
1.1 Определение недостающих геометрических размеров И.М
Расчёт диаметра делительной окружности приводной звёздочки производим по формуле:
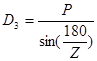 ,
,
где P – шаг тяговой цепи, мм;
Z- число зубьев звёздочки;
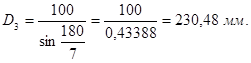
1.2 Определение потребной мощности и выбор электродвигателя
Номинальный вращающий момент на валу И. М. найдём по формуле:
![]() ,
,
где ![]() - окружное усилие на рабочем элементе И.М., кН;
- окружное усилие на рабочем элементе И.М., кН;
![]() - диаметр звёздочки, мм.
- диаметр звёздочки, мм.
![]()
Расчёт эквивалентного вращающего момента производим следующим образом:
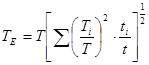 ,
,
где ![]() - ступени нагрузки (момента) и соответствующее ей время работы по графику нагрузки;
- ступени нагрузки (момента) и соответствующее ей время работы по графику нагрузки;
t- общее время работы под нагрузкой.
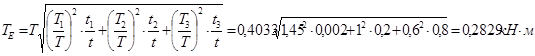 .
.
Угловая скорость вращения вала И.М.:
![]() ,
,
где V- скорость цепи конвейера, м/с.
![]() .
.
Общий КПД привода найдём как произведение КПД отдельных звеньев кинематической цепи:
![]() ,
,
где ![]() = 0,98 – КПД соединительной муфты;
= 0,98 – КПД соединительной муфты;
![]() = 0,99 – КПД пары подшипников качения;
= 0,99 – КПД пары подшипников качения;
![]() = 0,98 – КПД цилиндрической закрытой зубчатой передачи.
= 0,98 – КПД цилиндрической закрытой зубчатой передачи.
![]() .
.
Расчётная мощность электродвигателя в киловаттах определяется по зависимости:
![]() .
.
![]()
Частота вращения вала И.М.:
![]() .
.
![]() .
.
Возможный диапазон общего передаточного числа кинематической схемы привода:
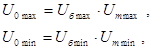
где ![]() ,
, ![]() - соответственно максимальное передаточное число быстроходной и тихоходной ступени передач;
- соответственно максимальное передаточное число быстроходной и тихоходной ступени передач;
![]() ,
, ![]() - соответственно минимальное передаточное число быстроходной и тихоходной ступени передач.
- соответственно минимальное передаточное число быстроходной и тихоходной ступени передач.
Твёрдость зубьев HRC 56
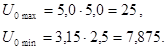
Возможный диапазон асинхронной частоты вращения вала электродвигателя:
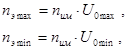
где ![]() ,
, ![]() - соответственно максимальная и минимальная (для заданной кинематической схемы привода) расчётная частота вращения вала электродвигателя, об/мин.
- соответственно максимальная и минимальная (для заданной кинематической схемы привода) расчётная частота вращения вала электродвигателя, об/мин.
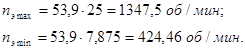
Выбираем электродвигатель по условиям:
![]() ,
, ![]() ,
,
где ![]() ,
, ![]() - табличные значения соответственно мощности, кВт и частоты вращения вала, об/мин.
- табличные значения соответственно мощности, кВт и частоты вращения вала, об/мин.
![]() 1,838 кВт;
1,838 кВт; ![]()
![]()
![]()
| 4A112 MA 6УЗ |
|
|
|
| 4А112 MB 8УЗ |
|
|
|
Проверку выбранных двигателей на перегрузку производим по условию:
![]() ,
,
где ![]() - номинальная мощность двигателя по каталогу, кВт;
- номинальная мощность двигателя по каталогу, кВт;
![]() - максимальный момент при эксплуатации (по графику нагрузки), кНм;
- максимальный момент при эксплуатации (по графику нагрузки), кНм;
![]() - асинхронная частота вращения вала электродвигателя по каталогу, об/мин;
- асинхронная частота вращения вала электродвигателя по каталогу, об/мин;
![]() - кратность пускового момента по каталогу на электродвигатель.
- кратность пускового момента по каталогу на электродвигатель.
Общее передаточное число привода находим по формуле:
![]() .
.
Проверяем 1-й двигатель:
![]()
![]() - условие выполняется.
- условие выполняется.
Проверяем 2-й двигатель:
![]()
![]() - условие выполняется.
- условие выполняется.
1.3 Разбивка общего передаточного числа редуктора по ступеням передач
![]() .
.
Разбивку производим с использованием формул:
![]() ,
,
где ![]() - передаточное число тихоходной ступени 2-х ступенчатого редуктора.
- передаточное число тихоходной ступени 2-х ступенчатого редуктора.
![]() ,
,
где ![]() - передаточное число быстроходной ступени 2-х ступенчатого редуктора.
- передаточное число быстроходной ступени 2-х ступенчатого редуктора.
Точность разбивки общего передаточного числа проверяем условием:
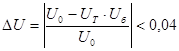 .
.
При использовании 1-го двигателя:
![]() ;
;
![]() ;
;
![]() .
.
С учётом стандартного ряда передаточных чисел имеем:
![]() ;
; ![]() .
.
![]() - условие не выполняется.
- условие не выполняется.
При использовании 2-го двигателя:
![]() ;
;
![]() ;
;
![]() .
.
С учётом стандартного ряда передаточных чисел имеем:
![]() ;
; ![]() .
.
![]() - условие выполняется.
- условие выполняется.
Принимаем 2-й двигатель.
Зарисовываем эскиз выбранного электродвигателя с указанием его основных характеристик.
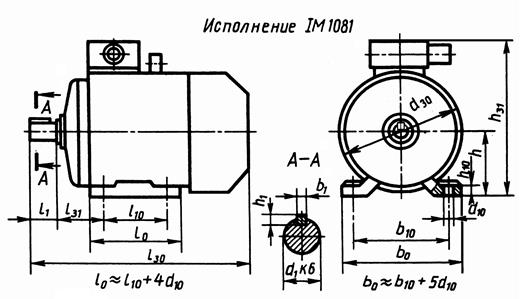
Рисунок 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 10 |
452 |
70 |
260 |
112 |
32 |
12 |
80 |
140 |
310 |
190 |
12 |
8 |
1.4 Составление таблицы исходных данных
Номинальная расчётная мощность электродвигателя:
![]() .
.
![]()
| № валов |
|
|
|
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
| 4 |
|
|
|
Проводим проверку правильности расчётов с использованием примерных равенств:
![]() ;
; ![]() .
.
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
;
![]()
2. Проектирование редуктора
2.1 Расчёт первой ступени редуктора. Предварительные расчёты
2.1.1 Номинальное значение вращающего момента на валу шестерни ![]() , Нм:
, Нм:
![]() .
.
2.1.2 Выбор материала для зубчатых колёс
Марка стали шестерни: 40ХН;
колеса: 40Х.
Выбираем второй режим термообработки: шестерня – ТВЧ;
колесо – У.
2.1.3 Допускаемые контактные напряжения определяем раздельно для шестерни и колеса по формуле:
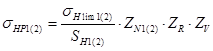
В качестве допускаемого контактного напряжения передачи для косозубых передач
принимаем:
![]()
при выполнении условия: ![]() ,
,
где ![]() - допускаемое контактное напряжение шестерни;
- допускаемое контактное напряжение шестерни;
![]() - допускаемое контактное напряжение колеса;
- допускаемое контактное напряжение колеса;
![]() - предел контактной выносливости:
- предел контактной выносливости:
![]()
![]() - коэффициент запаса прочности:
- коэффициент запаса прочности:
![]()
![]()
![]() - коэффициент долговечности
- коэффициент долговечности
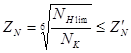 при
при ![]() ;
;
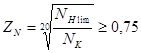 при
при ![]() ,
,
где ![]() - базовое число циклов напряжений, соответствующее пределу выносливости:
- базовое число циклов напряжений, соответствующее пределу выносливости:
![]() ,
,
где ![]() - среднее значение твёрдости рабочей поверхности зубьев.
- среднее значение твёрдости рабочей поверхности зубьев.
![]() ;
;
![]() ;
;
![]() .
.
![]() - число циклов напряжений в соответствии с заданным сроком службы.
- число циклов напряжений в соответствии с заданным сроком службы.
![]() ,
,
где ![]() - ресурс передачи, ч;
- ресурс передачи, ч;
![]()
При нагрузке на передачу, изменяющейся по ступенчатой циклограмме,:
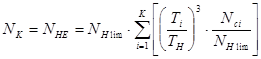 .
.
![]() ;
;
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() - коэффициент, учитывающий шероховатость сопряжённых поверхностей зубьев:
- коэффициент, учитывающий шероховатость сопряжённых поверхностей зубьев:
![]()
![]() - коэффициент, учитывающий окружную скорость.
- коэффициент, учитывающий окружную скорость.
![]()
![]()
где V- окружная скорость передачи, м/с.
При проектировочном расчёте принимаем ![]()
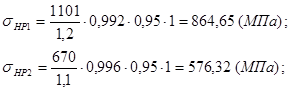
![]()
![]()
![]()
2.1.4 Допускаемые напряжения изгиба зубьев определяем раздельно для шестерни и колеса по формуле:
![]() ,
,
где ![]() - предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, установлен от нулевого цикла напряжений и определяется в зависимости от способа термической или химико-термической обработки:
- предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, установлен от нулевого цикла напряжений и определяется в зависимости от способа термической или химико-термической обработки:
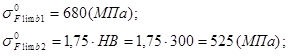
![]() - коэффициент, учитывающий способ получения заготовки зубчатого колеса.
- коэффициент, учитывающий способ получения заготовки зубчатого колеса.
![]() - для поковок и штамповок;
- для поковок и штамповок;
![]() - коэффициент, учитывающий влияние двустороннего приложения нагрузки:
- коэффициент, учитывающий влияние двустороннего приложения нагрузки:
![]()
![]() - коэффициент долговечности:
- коэффициент долговечности: 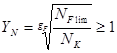
![]() - базовое число циклов напряжений,
- базовое число циклов напряжений, ![]() .
.
При нагрузке на передачу, изменяющейся по ступенчатой циклограмме,:
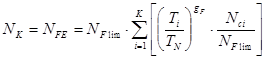 .
.
Произведя аналогичные преобразования, что и в пункте 2.1.3, получим:
![]()
![]() ;.
;.
![]() .
.
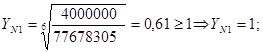
![]()
Для зубчатых колёс с однородной структурой материала, включая закалённые при нагреве ТВЧ со сквозной закалкой, ![]() При этом
При этом ![]()
![]() - коэффициент, учитывающий диаметр зубчатого колеса в мм.;
- коэффициент, учитывающий диаметр зубчатого колеса в мм.;
![]()
При проведении проектировочного расчёта принимаем ![]() .
.
![]() - коэффициент запаса прочности. Принимают в зависимости от способа термической или химико-термической обработки при вероятности неразрушения 0,99.
- коэффициент запаса прочности. Принимают в зависимости от способа термической или химико-термической обработки при вероятности неразрушения 0,99.
![]()
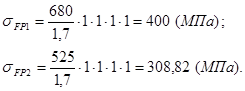
2.1.5 Допускаемое напряжение изгиба зубьев для расчёта на изгиб максимальной нагрузкой определяют раздельно для зубчатых колёс пары по формуле:
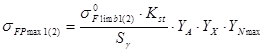 ,
,
где ![]() - коэффициент, учитывающий различие между предельными напряжениями, определёнными при ударном однократном нагружении и при числе ударных нагружений
- коэффициент, учитывающий различие между предельными напряжениями, определёнными при ударном однократном нагружении и при числе ударных нагружений ![]() .
.
Принимаем при ![]() 6
6 ![]() 1,3.
1,3.
![]() - коэффициент, зависящий от вероятности неразрушения.
- коэффициент, зависящий от вероятности неразрушения.
При вероятности неразрушения 0,99 ![]() .
.
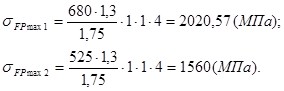
2.1.6 Параметр ![]() определяет рабочую ширину венца зубчатой передачи
определяет рабочую ширину венца зубчатой передачи ![]() при известном начальном диаметре шестерни
при известном начальном диаметре шестерни ![]() или наоборот
или наоборот
![]()
2.1.7 Выбираем угол наклона зуба ![]() :
:
![]()
2.1.8 Определяем начальный диаметр шестерни по формуле, мм:
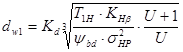 ,
,
где ![]() - исходная расчётная нагрузка, в качестве которой принимается наибольший из действующих на шестерню вращающий момент в
- исходная расчётная нагрузка, в качестве которой принимается наибольший из действующих на шестерню вращающий момент в ![]() , для которого число циклов перемен напряжений не менее
, для которого число циклов перемен напряжений не менее ![]() ;
;
![]()
![]()
![]()
![]()
U- передаточное число передачи; U=4;
![]() - допускаемые контактные напряжения, МПа;
- допускаемые контактные напряжения, МПа;
![]() - вспомогательный коэффициент.
- вспомогательный коэффициент.
Для косозубых передач ![]() ;
;
![]() - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий.
- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий. ![]()

2.1.9 Определяем ширину зубчатого венца и полученные значения округляем до ближайшего значения по ГОСТ 6636-69:
колеса ![]() ,
,
![]()
шестерни ![]() .
.
![]()
2.1.10 Ориентировочное значение модуля вычисляем по формуле:
![]() ,
,
где ![]() - исходная расчётная нагрузка на шестерню, в качестве которой принимается наибольший длительно действующий вращающий момент,
- исходная расчётная нагрузка на шестерню, в качестве которой принимается наибольший длительно действующий вращающий момент, ![]() , с числом циклов перемен напряжений более
, с числом циклов перемен напряжений более ![]() ;
;
![]()
![]() - вспомогательный коэффициент. Для косозубых передач
- вспомогательный коэффициент. Для косозубых передач ![]()
![]() - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий.
- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий. ![]()
![]()
2.1.11 Определяем число зубьев шестерни по формуле:
![]() ,
,
![]()
![]()
число зубьев колеса: ![]() .
.
![]()
Расчёт геометрических и кинематических параметров передачи
2.1.12 Делительное межосевое расстояние, мм:
![]() .
.
![]()
Принимаем ![]()
2.1.13 Угол наклона зуба:
![]() ,
,
![]()
где ![]() - начальное межосевое расстояние, принятое для изготовления передачи.
- начальное межосевое расстояние, принятое для изготовления передачи.
2.1.14 Основной угол наклона зуба:
![]() .
.
![]()
2.1.15 Делительный угол профиля в торцевом сечении:
![]() .
.
![]()
2.1.16 Начальный диаметр, мм:
шестерни ![]() ,
,
![]()
колеса ![]() .
.
![]()
2.1.17 Делительный диаметр, мм:
шестерни ![]() ,
,
![]()
колеса ![]() .
.
![]()
2.1.18 Диаметр вершин зубьев, мм:
шестерни ![]() ,
,
![]()
колеса ![]() .
.
![]()
2.1.19 Диаметр впадин, мм:
шестерни ![]() ,
,
![]()
колеса ![]() .
.
![]()
2.1.20 Основной диаметр, мм:
шестерни ![]() ,
,
![]()
колеса ![]() .
.
![]()
2.1.21 Коэффициент торцевого перекрытия:
![]() ,
,
где ![]() ;
; ![]() .
.
2.1.22 Коэффициент осевого перекрытия:
![]() .
.
![]()
2.1.23 Суммарный коэффициент перекрытия:
![]() .
.
![]()
2.1.24 Эквивалентное число зубьев:
шестерни ![]() ,
,
![]()
колеса ![]() .
.
![]()
2.1.25 Окружная скорость, м/с:
![]() .
.
![]()
Проверочные расчёты передачи
2.1.26 Проверочный расчёт на контактную выносливость:
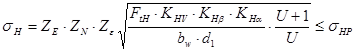 ,
,
где ![]() - коэффициент, учитывающий механические свойства материалов сопряжённых зубчатых колёс.
- коэффициент, учитывающий механические свойства материалов сопряжённых зубчатых колёс.
Для стальных передач при ![]() ;
;
![]() - коэффициент, учитывающий форму сопряжённых поверхностей зубьев в полюсе зацепления:
- коэффициент, учитывающий форму сопряжённых поверхностей зубьев в полюсе зацепления:
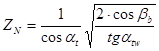 ;
;
![]()
![]() - коэффициент, учитывающий суммарную длину контактных линий:
- коэффициент, учитывающий суммарную длину контактных линий:
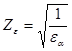 при
при ![]() ,
,
![]()
![]() - окружная сила на делительном цилиндре, Н:
- окружная сила на делительном цилиндре, Н:
![]() ;
;
![]()
![]() - коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса:
- коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса:
![]() ;
;
![]() - удельная окружная динамическая сила, Н/мм:
- удельная окружная динамическая сила, Н/мм:
![]() ,
,
где ![]() - коэффициент, учитывающий влияние вида зубчатой передачи:
- коэффициент, учитывающий влияние вида зубчатой передачи:
![]()
![]()
![]() - коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса;
- коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса; ![]()
![]() - предельное значение удельной окружной динамической силы;
- предельное значение удельной окружной динамической силы;
![]()
![]()
![]()
![]() - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий:
- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий: ![]() ,
,
![]() - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий в начальный период работы передачи.
- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий в начальный период работы передачи.
Для прямозубых и косозубых передач
![]() :
: ![]()
где ![]() =0,14 при расположении шестерни на валу передачи со стороны подвода вращающего момента.
=0,14 при расположении шестерни на валу передачи со стороны подвода вращающего момента.
![]()
![]() - коэффициент, учитывающий приработку зубьев:
- коэффициент, учитывающий приработку зубьев:
![]() ,
,
![]() - твёрдость менее твёрдого зубчатого колеса передачи.
- твёрдость менее твёрдого зубчатого колеса передачи.
![]() - коэффициент, учитывающий распределение нагрузки между зубьями.
- коэффициент, учитывающий распределение нагрузки между зубьями.
Для косозубых передач:
![]() и 7-й степени точности,
и 7-й степени точности,
при условии, что ![]() .
.
![]()
Учтём коэффициенты ![]() :
:
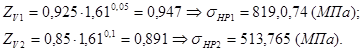
![]()
![]()
2.1.27 Расчёт на контактную прочность при действии максимальной нагрузки:
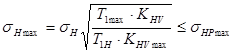 ,
,
где ![]() - наибольший вращающий момент на валу шестерни, Нм;
- наибольший вращающий момент на валу шестерни, Нм;
![]()
![]() - коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении при нагрузке
- коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении при нагрузке ![]() :
: ![]() ;
;
![]()
![]() - допускаемое контактное напряжение при максимальной нагрузке, не вызывающее остаточных деформаций или хрупкого разрушения поверхностного слоя, МПа.
- допускаемое контактное напряжение при максимальной нагрузке, не вызывающее остаточных деформаций или хрупкого разрушения поверхностного слоя, МПа.
Для зубьев, подвергнутых цементации или контурной закалке:![]() .
.
![]()
Для зубчатых колёс, подвергнутых нормализации, улучшению или сквозной закалке с низким отпуском:
![]()
Где ![]() - предел текучести, МПа.
- предел текучести, МПа.
Для стали 40Х ![]() . (см.[1], с.114)
. (см.[1], с.114)
![]()
![]()
![]()
![]()
2.1.28 Расчёт зубьев на выносливость при изгибе:
![]() ,
,
где ![]() - окружная сила на делительном цилиндре, Н:
- окружная сила на делительном цилиндре, Н:
![]()
![]()
![]() -коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса:
-коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса:
![]() .
.
![]() ,
,
где ![]() - коэффициент, учитывающий влияние вида зубчатой передачи.
- коэффициент, учитывающий влияние вида зубчатой передачи.
![]() для косозубых передач.
для косозубых передач.
![]() - коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса;
- коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса; ![]()
![]() - предельное значение удельной окружной динамической силы;
- предельное значение удельной окружной динамической силы;
![]()
![]()
![]()
![]() - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий:
- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий:
![]() ,
,
где 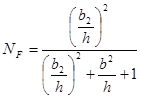 ,
,
![]() - для косозубого зацепления;
- для косозубого зацепления;
![]()
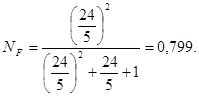
![]()
![]() - коэффициент, учитывающий распределение нагрузки между зубьями.
- коэффициент, учитывающий распределение нагрузки между зубьями.
![]() для косозубых передач,
для косозубых передач,
где СТ – степень точности передачи.
![]() - коэффициент, учитывающий форму зуба и концентрацию напряжений:
- коэффициент, учитывающий форму зуба и концентрацию напряжений:
![]() ,
,
![]()
![]() ;
;
![]()
![]() - коэффициент, учитывающий наклон зуба:
- коэффициент, учитывающий наклон зуба:
![]() ;
;
![]()
![]() -коэффициент, учитывающий перекрытие зубьев.
-коэффициент, учитывающий перекрытие зубьев.
При ![]()
![]()
![]()
![]()
2.1 29 Расчёт на прочность при изгибе максимальной нагрузкой
Прочность зубьев, необходимую для предотвращения остаточных деформаций, хрупкого излома или образования первичных трещин в поверхностном слое, определяют сопоставлением расчётного и допускаемого напряжений изгиба в опасном сечении при действии максимальной нагрузки:
![]() ,
,
где ![]() - расчётное местное напряжение при изгибе;
- расчётное местное напряжение при изгибе;
![]() - окружная сила на делительном цилиндре;
- окружная сила на делительном цилиндре;
![]() - максимальная из действующих за расчётный срок окружная сила на делительном цилиндре ударного или плавного характера с числом повторных воздействий
- максимальная из действующих за расчётный срок окружная сила на делительном цилиндре ударного или плавного характера с числом повторных воздействий ![]() :
:
![]() .
.
![]()
![]()
2.1.30 Расчёт усилий зубчатого зацепления
Окружное усилие, Н:
![]() ;
;
![]()
Радиальное усилие, Н:
![]() ;
;
![]()
Осевое усилие, Н:
![]() ;
;
![]()
2.2 Расчёт второй ступени редуктора. Предварительные расчёты
2.2.1 Номинальное значение вращающего момента на валу шестерни ![]() , Нм:
, Нм:
![]()
2.2.2 Выбор материала для зубчатых колёс
Марка стали шестерни: 40ХН;
колеса: 40Х.
Выбираем второй режим термообработки: шестерня – ТВЧ;
колесо – У.
2.2.3 Допускаемые контактные напряжения:
![]()
![]()
![]()
![]() ;
;
![]() .
.
![]() ;
;
![]() ;
;
![]()
![]()
![]()
При проектировочном расчёте принимаем ![]()
2.2.4 Допускаемые напряжения изгиба зубьев:
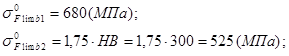
![]() - для поковок и штамповок;
- для поковок и штамповок;
![]()
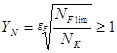 .
.
![]() .
.
![]() При этом
При этом ![]()
При нагрузке на передачу, изменяющейся по ступенчатой циклограмме,:
![]()
![]() .
.
![]() .
.
![]()
![]()
При проведении проектировочного расчёта принимаем ![]() .
.
![]()
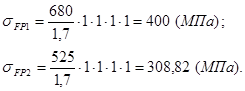
2.2.5 Допускаемое напряжение изгиба зубьев для расчёта на изгиб максимальной нагрузкой:
Принимаем при ![]() 6
6 ![]() 1,3.
1,3.
При вероятности неразрушения 0,99 ![]() .
.
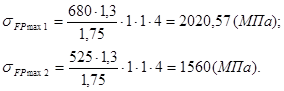
2.2.6 ![]()
Проектировочный расчёт
2.2.7 Определяем начальный диаметр шестерни:
![]()
![]()
![]()
![]() ;
;
U=3,15;
Для прямозубых передач ![]() ;
;
![]()
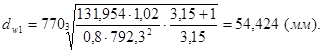
2.2.8 Определяем ширину зубчатого венца и полученные значения округляем до ближайшего значения по ГОСТ 6636-69:
колеса ![]()
шестерни ![]()
2.2.9 Ориентировочное значение модуля:
![]()
Для прямозубых передач ![]()
![]()
![]()
2.2.10 Число зубьев шестерни:
![]()
![]()
![]()
Расчёт геометрических и кинематических параметров передачи
2.2.11 Делительное межосевое расстояние, мм:
![]()
Принимаем ![]()
2.2.12 Угол наклона зуба:
![]() .
.
2.2.13 Основной угол наклона зуба:
![]()
2.2.14 Делительный угол профиля в торцевом сечении:
![]()
2.2.15 Угол зацепления при выполнении передачи со смещением:
![]()
2.2.16 Коэффициент суммы смещений:
![]() ;
;
![]()
2.2.17 Начальный диаметр, мм:
шестерни ![]()
колеса ![]()
2.2.18 Коэффициент воспринимаемого смещения:
![]()
2.2.19 Коэффициент уравнительного смещения:
![]()
2.2.20 Делительный диаметр, мм:
шестерни ![]()
колеса ![]()
2.2.21 Диаметр вершин зубьев, мм:
шестерни ![]()
колеса ![]()
2.2.22 Диаметр впадин, мм:
шестерни ![]()
колеса ![]()
2.2.23 Основной диаметр, мм:
шестерни ![]()
колеса ![]()
2.2.24 Коэффициент торцевого перекрытия:
![]() ;
;
![]()
![]()
2.2.25 Коэффициент осевого перекрытия:
![]()
2.2.26 Суммарный коэффициент перекрытия:
![]()
2.2.27 Эквивалентное число зубьев:
шестерни ![]() ,
,
колеса ![]()
2.2.28 Окружная скорость:
![]()
Проверочные расчёты передачи
2.2.28 Проверочный расчёт на контактную выносливость:
Для стальных передач при ![]() ;
;
![]()
При ![]()
![]()
![]() - окружная сила на делительном цилиндре, Н:
- окружная сила на делительном цилиндре, Н:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =0,14.
=0,14.
![]()
![]()
![]()
![]() - коэффициент, учитывающий распределение нагрузки между зубьями.
- коэффициент, учитывающий распределение нагрузки между зубьями.
Для прямозубых передач: ![]() .
.
Учтём коэффициенты ![]() :
:
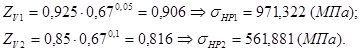
![]()
![]()
2.2.29 Расчёт на контактную прочность при действии максимальной нагрузки:
![]()
![]()
Для зубьев, подвергнутых цементации или контурной закалке:![]() .
.
![]()
Для зубчатых колёс, подвергнутых нормализации, улучшению или сквозной закалке с низким отпуском: ![]()
2.2.30 Расчёт зубьев на выносливость при изгибе:
![]()
![]() для прямозубых передач;
для прямозубых передач; ![]()
![]()
![]()
![]()
![]() - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий:
- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий: ![]() ,
,
где 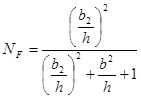 ,
,
![]() - для прямозубого зацепления;
- для прямозубого зацепления;
![]()
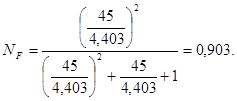
![]()
![]() - коэффициент, учитывающий распределение нагрузки между зубьями.
- коэффициент, учитывающий распределение нагрузки между зубьями.
![]() для прямозубых передач,
для прямозубых передач,
![]() - коэффициент, учитывающий форму зуба и концентрацию напряжений:
- коэффициент, учитывающий форму зуба и концентрацию напряжений:
![]() ,
,
![]() ;
;
![]() - коэффициент, учитывающий наклон зуба:
- коэффициент, учитывающий наклон зуба:
![]() ;
;
![]() -коэффициент, учитывающий перекрытие зубьев.
-коэффициент, учитывающий перекрытие зубьев.
При ![]()
![]()
![]()
2.2.31 Расчёт на прочность при изгибе максимальной нагрузкой
![]()
![]()
![]()
2.2.32 Расчёт усилий зубчатого зацепления
![]()
![]()
![]()
2.3 Расчёт валов редуктора
2.3.1 Проверка сечений валов
Быстроходный вал
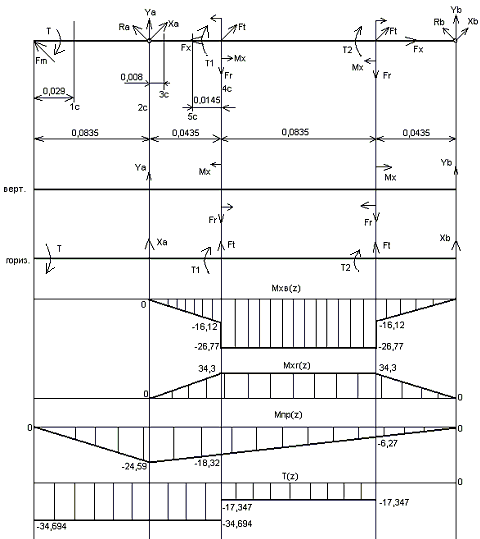
Рисунок 2
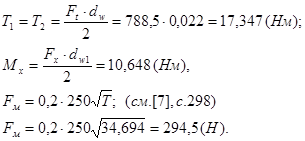
Эпюра изгибающего момента для вертикальной плоскости
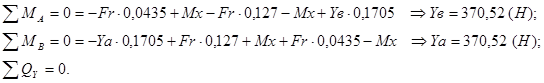
![]()
![]()
![]()
![]()
Эпюра изгибающего момента для горизонтальной плоскости
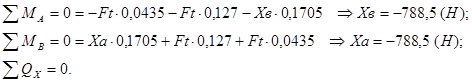
![]()
![]()
![]()
![]()
Эпюра изгибающего момента для произвольной плоскости
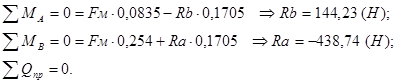
![]()
![]()
![]()
Эпюра крутящего момента
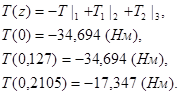
Расчёт 1-го сечения
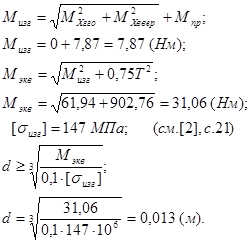
Расчёт 2-го сечения
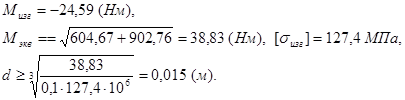
![]()
Расчёт 3-го сечения
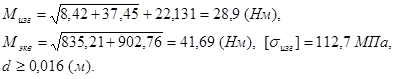
![]()
Расчёт 4-го сечения
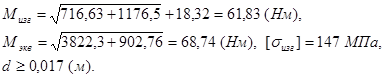
Расчёт 5-го сечения
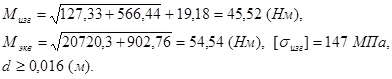
Промежуточный вал
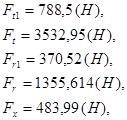
![]()
Эпюра изгибающего момента для вертикальной плоскости
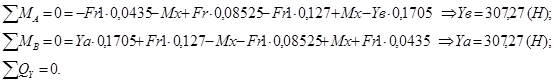
![]()
![]()
![]()
![]()
![]()
Рисунок 3
Эпюра изгибающего момента для горизонтальной плоскости
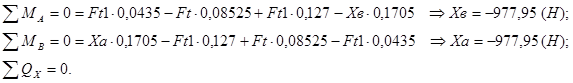
![]()
![]()
![]()
![]()
![]()
Эпюра крутящего момента

Расчёт 1-го сечения
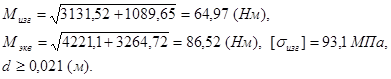
![]()
Расчёт 2-го сечения
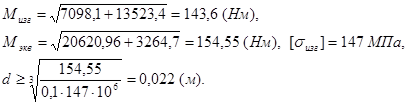
Расчёт 3-го сечения
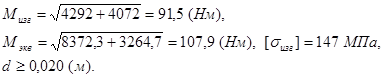
Тихоходный вал
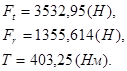
![]()
Эпюра изгибающего момента для вертикальной плоскости
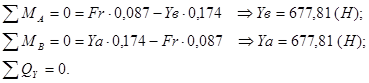
![]()
![]()
Рисунок 4
![]()
Эпюра изгибающего момента для горизонтальной плоскости
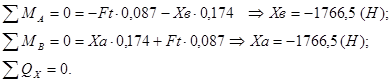
![]()
![]()
![]()
![]()
Эпюра изгибающего момента для произвольной плоскости
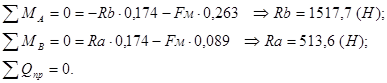
![]()
![]()
![]()
Эпюра крутящего момента
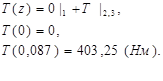
Расчёт 1-го сечения
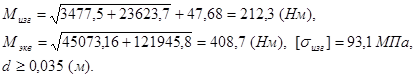
Расчёт 2-го сечения
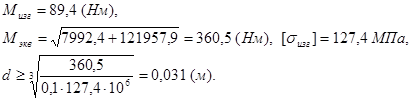
Расчёт 3-го сечения
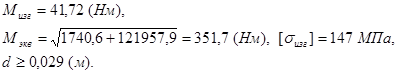
Расчёт 4-го сечения
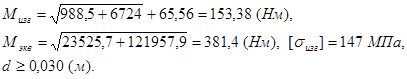
2.3.2 Расчет валов редуктора на статическую прочность
Проверку статической прочности выполняют в целях предупреждения пластических деформаций в период действия кратковременных перегрузок (например, при пуске, разгоне).
Коэффициент перегрузки ![]()
![]() ,
, ![]() ,
,
где ![]() - нормальные напряжения;
- нормальные напряжения;
![]() - касательные напряжения;
- касательные напряжения;
![]() - суммарный изгибающий момент, Н
- суммарный изгибающий момент, Н![]() м;
м;
![]() - максимальный крутящий момент, Н
- максимальный крутящий момент, Н![]() м;
м;
![]() - максимальная осевая сила, Н;
- максимальная осевая сила, Н;
![]() - моменты сопротивления сечения вала при расчете на изгиб и кручение, м
- моменты сопротивления сечения вала при расчете на изгиб и кручение, м![]() ;
;
А – площадь поперечного сечения, м![]() .
.
![]() ;
; ![]()
где ![]() ,
, ![]() - частные коэффициенты запаса прочности по нормальным и касательным напряжениям;
- частные коэффициенты запаса прочности по нормальным и касательным напряжениям;
![]() - пределы текучести материала.
- пределы текучести материала. ![]() - характеристики стали 40ХН при диаметре заготовки
- характеристики стали 40ХН при диаметре заготовки ![]() .
.
![]()
где ![]() - общий коэффициент запаса прочности по пределу текучести при совместном действии нормальных и касательных напряжений. Статическую прочность считают обеспеченной, если
- общий коэффициент запаса прочности по пределу текучести при совместном действии нормальных и касательных напряжений. Статическую прочность считают обеспеченной, если ![]() , где
, где ![]() - минимально допустимое значение общего коэффициента запаса по текучести.
- минимально допустимое значение общего коэффициента запаса по текучести.
Принимаем ![]() .
.
Быстроходный вал
Расчёт 1-го сечения
![]()
Моменты сопротивления сечения вала с одним шпоночным пазом:
![]()
где b – ширина шпонки, h – высота шпонки.
![]()
![]()
![]()
![]()
![]()
Расчёт 2-го сечения
![]()
Моменты сопротивления сечения вала:
![]()
![]()
![]()
![]()
![]()
![]()
Расчёт 3-го сечения
![]()
![]()
![]()
![]()
![]()
![]()
Расчёт 4-го сечения
![]()
Моменты сопротивления вала-шестерни в сечении по зубьям:
![]() ,
, ![]()
где J – момент инерции, ![]() ;
; ![]() - диаметр вершин, м.
- диаметр вершин, м.
![]() =0,04878 м.
=0,04878 м.
![]()
где ![]() -принимают в зависимости от коэффициента смещения Х и числа зубьев Z;
-принимают в зависимости от коэффициента смещения Х и числа зубьев Z;
Х=0, Z=25 (эквивалентное число зубьев),![]() =0,98;
=0,98;
d – диаметр делительной окружности, м. d=0,044 м.
![]() (м
(м![]() ),
),
![]() (м
(м![]() ),
), ![]() (м
(м![]() ).
).
![]()
![]()
![]()
Расчёт 5-го сечения
![]()
![]()
![]()
![]()
![]()
![]()
Промежуточный вал
Расчёт 1-го сечения
![]()
![]()
![]()
![]()
![]()
![]()
Расчёт 2-го сечения
![]()
![]() ,
, ![]()
![]() =0,082502 м.
=0,082502 м.
![]() .
.
Х=0,29, Z=21,![]() =1,01;
=1,01;
d=0,0735 мм.
![]() (м
(м![]() ),
),
![]() (м
(м![]() ),
), ![]() (м
(м![]() ).
).
![]()
![]()
![]()
Расчёт 3-го сечения
![]()
![]()
![]()
![]()
![]()
![]()
Тихоходный вал
Расчёт 1-го сечения
![]()
![]()
![]()
![]()
![]()
![]()
Расчёт 2-го сечения
![]()
![]()
![]()
![]()
![]()
![]()
Расчёт 3-го сечения
![]()
![]()
![]()
![]()
![]()
![]()
Расчёт 4-го сечения
![]()
![]()
![]()
![]()
![]()
![]()
2.3.3 Расчёт тихоходного вала на сопротивление усталости
Для каждого из установленных опасных сечений вычисляем коэффициент запаса прочности:
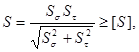
где ![]() - коэффициенты запаса по нормальным и касательным напряжениям:
- коэффициенты запаса по нормальным и касательным напряжениям:
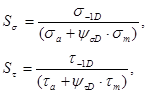
где ![]() - амплитуды напряжений цикла;
- амплитуды напряжений цикла; ![]() - средние напряжения цикла;
- средние напряжения цикла; ![]() - коэффициенты чувствительности к асимметрии цикла напряжений для рассматриваемого сечения;
- коэффициенты чувствительности к асимметрии цикла напряжений для рассматриваемого сечения;
![]() - коэффициент запаса прочности,
- коэффициент запаса прочности, ![]() Принимаем [S]=2,5.
Принимаем [S]=2,5.
В расчёте валов принимаем, что нормальные напряжения изменяются по симметричному циклу:
![]() , а касательные напряжения – по отнулевому циклу:
, а касательные напряжения – по отнулевому циклу: ![]() .
.
Напряжения в опасных сечениях вычисляем по формулам:
![]()
где ![]() - результирующий изгибающий момент, Нм;
- результирующий изгибающий момент, Нм; ![]() - крутящий момент
- крутящий момент
(![]() ), Нм;
), Нм; ![]() и
и ![]() - моменты сопротивления сечения вала при изгибе и кручении,
- моменты сопротивления сечения вала при изгибе и кручении, ![]() :
:
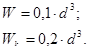
Пределы выносливости вала в рассматриваемом сечении:
![]()
где ![]() и
и ![]() - пределы выносливости гладких образцов при симметричном цикле изгиба и кручения;
- пределы выносливости гладких образцов при симметричном цикле изгиба и кручения; ![]() и
и ![]() - коэффициенты снижения предела выносливости.
- коэффициенты снижения предела выносливости.
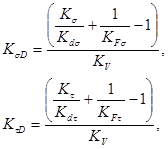
где ![]() и
и ![]() - эффективные коэффициенты концентрации напряжений;
- эффективные коэффициенты концентрации напряжений; ![]() и
и ![]() - коэффициенты влияния абсолютных размеров поперечного сечения;
- коэффициенты влияния абсолютных размеров поперечного сечения; ![]() и
и ![]() - коэффициенты влияния качества поверхности;
- коэффициенты влияния качества поверхности; ![]() - коэффициент влияния поверхностного упрочнения.
- коэффициент влияния поверхностного упрочнения.
Коэффициент влияния асимметрии цикла для рассматриваемого сечения вала
![]()
где ![]() - коэффициент чувствительности материала к асимметрии цикла напряжений.
- коэффициент чувствительности материала к асимметрии цикла напряжений.
Для 1-го сечения
![]()
![]()
![]()
![]()
![]()
![]()
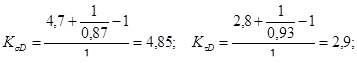
![]()
![]()
![]()
Для 2-го сечения
![]()
![]()
![]()
![]()
![]()
![]()
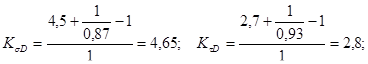
![]()
![]()
![]()
Для 3- го сечения
![]()
![]()
![]()
![]()
![]()
![]()
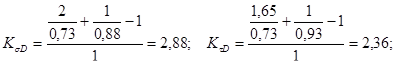
![]()
![]()
![]()
Для 4- го сечения
![]()
![]()
![]()
![]()
![]()
![]()
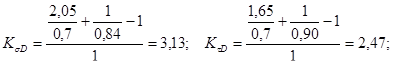
![]()
![]()
![]()
2.3.4 Расчет тихоходного вала на жесткость
Определение прогиба тихоходного вала в зубчатом зацеплении.
Для валов зубчатых передач стрела прогиба под колесом:
![]() (см.[2], стр. 16)
(см.[2], стр. 16)
Приведем вал к эквивалентному валу с постоянным сечением по формуле:
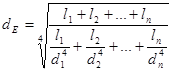 ,
,
где ![]() - длина n-го участка;
- длина n-го участка;
![]() - диаметр n-го участка.
- диаметр n-го участка.
![]() мм,
мм, ![]() мм;
мм; ![]() мм,
мм, ![]() мм;
мм; ![]() мм,
мм, ![]() мм;
мм;
![]() мм,
мм, ![]() мм;
мм;
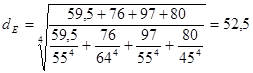 (мм)
(мм)
Для расчета прогиба воспользуемся интегралом Мора (см.[9], стр.199):
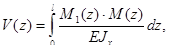
где ![]() - изгибающий момент от единичной нагрузки, Нм;
- изгибающий момент от единичной нагрузки, Нм;
![]() - изгибающий момент от реальной нагрузки, Нм;
- изгибающий момент от реальной нагрузки, Нм;
E – модуль Юнга (для стали ![]() );
);
![]() - осевой момент инерции,
- осевой момент инерции, ![]() .
.
![]()
В точке, где нам необходимо найти прогиб, прикладываем единичную нагрузку и составляем уравнения моментов от этой нагрузки.
Рисунок 5
Уравнение изгибающего момента для вертикальной плоскости:
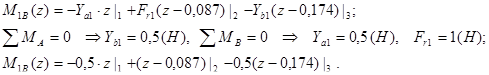
Уравнение изгибающего момента для горизонтальной плоскости:
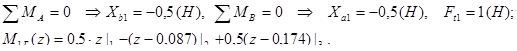
Уравнение изгибающего момента для произвольной плоскости
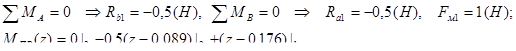
Используя уравнения изгибающих моментов от реальной нагрузки, полученные в пункте 2.3.1, найдём прогиб для каждой из указанных плоскостей.
Расчёт прогиба для вертикальной плоскости:
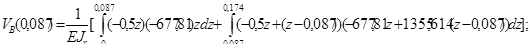
![]()
Расчёт прогиба для горизонтальной плоскости:
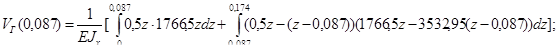
![]()
Расчёт прогиба для произвольной плоскости:
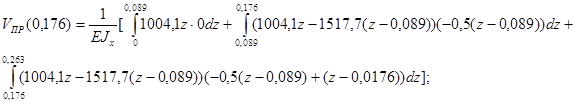
![]()
Суммарный прогиб найдём по формуле:
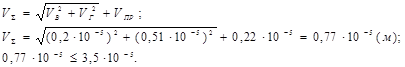
Определение углового перемещения тихоходного вала в зубчатом зацеплении
Допускаемое угловое перемещение вала в опорах:
для однорядных шарикоподшипников ![]() (см.[2], стр. 16)
(см.[2], стр. 16)
Дважды проинтегрируем по длине вала уравнения изгибающих моментов от реальной нагрузки, полученные в пункте 2.3.1.
Расчёт углового перемещения вала для вертикальной плоскости:
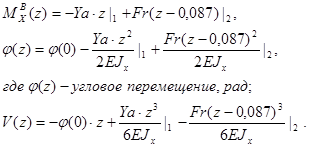
Начальные условия: ![]()
![]()
Для опоры A:
![]()
Для опоры B:
![]()
Расчёт углового перемещения вала для горизонтальной плоскости:
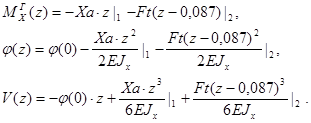
Начальные условия: ![]()
![]()
Для опоры A:
![]()
Для опоры B:
![]()
Расчёт углового перемещения вала для произвольной плоскости:
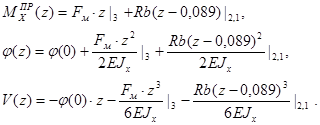
Начальные условия: ![]()
![]()
Для опоры A:
![]()
Для опоры B:
![]()
Суммарное угловое перемещение найдём по формуле:
![]()
Для опоры А:
![]()
![]()
Для опоры B:
![]()
![]()
Все условия выполняются. Вал проходит по расчёту на жёсткость.
2.4 Расчет подшипников редуктора
Тихоходный вал.
Расчет на статическую грузоподъемность.
Шариковые радиальные однорядные подшипники легкой серии, обозначение 211.
Базовая статическая радиальная грузоподъемность ![]()
![]()
![]()
где ![]() - реакция в подшипнике в вертикальной плоскости, Н;
- реакция в подшипнике в вертикальной плоскости, Н;
![]() - реакция в подшипнике в горизонтальной плоскости, Н;
- реакция в подшипнике в горизонтальной плоскости, Н;
![]() - реакция в подшипнике от муфты, Н;
- реакция в подшипнике от муфты, Н;
![]()
![]() .
.
Расчет на заданный ресурс.
Исходные данные:
![]() - внешняя осевая сила, Н,
- внешняя осевая сила, Н,![]() =0;
=0;
d - диаметр посадочной поверхности, d=55 ![]() ;
;
![]() - требуемый ресурс при необходимой вероятности безотказной работы подшипника,
- требуемый ресурс при необходимой вероятности безотказной работы подшипника,![]() ;
;
![]() - базовая статическая радиальная грузоподъемность
- базовая статическая радиальная грузоподъемность ![]() ;
;
![]() - базовая динамическая радиальная грузоподъемность
- базовая динамическая радиальная грузоподъемность ![]() ;
;
![]() - радиальная нагрузка,
- радиальная нагрузка, ![]()
![]() ;
;
![]() .
.
![]() , X=1, Y=0.
, X=1, Y=0.
X, Y – коэффициенты радиальной и осевой нагрузок.
Эквивалентная динамическая нагрузка:
![]()
где V – коэффициент вращения кольца, V=1 при вращении внутреннего кольца;
![]() - коэффициент безопасности,
- коэффициент безопасности, ![]() ;
;
![]() - температурный коэффициент,
- температурный коэффициент, ![]() (рабочая температура
(рабочая температура ![]() ).
).
![]()
![]() ;
;
Для подшипников, работающих при переменных режимах нагружения, вычисляют эквивалентную радиальную![]() динамическую нагрузку при переменном режиме нагружения:
динамическую нагрузку при переменном режиме нагружения:
где ![]() и
и![]() - постоянная эквивалентная нагрузка на n-том режиме и продолжительность её действия в млн. об. Если
- постоянная эквивалентная нагрузка на n-том режиме и продолжительность её действия в млн. об. Если![]() задана в часах -
задана в часах - ![]() , то её пересчитывают на млн. об. с учетом частоты вращения
, то её пересчитывают на млн. об. с учетом частоты вращения ![]() :
:
![]() .
.
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
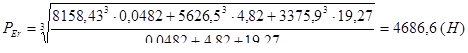
Определение скорректированного по уровню надежности и условиям применения расчетного ресурса подшипника, ч:
![]()
где С – базовая динамическая грузоподъемность, Н;
![]()
Р – эквивалентная динамическая нагрузка, Н;
k – показатель степени, k=3 для шариковых подшипников;
n – частота вращения кольца, ![]() ;
;
![]() - коэффициент долговечности в функции необходимой надежности,
- коэффициент долговечности в функции необходимой надежности, ![]() =1;
=1;
![]() - коэффициент, характеризующий совместное влияние на долговечность особых свойств металла деталей подшипника и условий его эксплуатации,
- коэффициент, характеризующий совместное влияние на долговечность особых свойств металла деталей подшипника и условий его эксплуатации, ![]() =0,75.
=0,75.
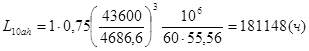 .
.
1811487227, ресурс подшипника больше необходимого.
Промежуточный вал
Расчет на статическую грузоподъемность
![]()
![]()
![]()
![]() ,
, ![]() .
.
Расчет на заданный ресурс.
Исходные данные:
![]() =0; d=35
=0; d=35 ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]()
![]() ;
; ![]() .
.
![]() , X=1, Y=0.
, X=1, Y=0.
Эквивалентная динамическая нагрузка:
![]()
![]() ;
;![]() ;
;
![]()
![]() ;
;
Эквивалентная радиальная динамическая нагрузка:
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
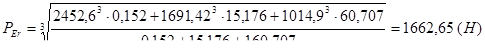
Определение расчетного ресурса подшипника:
![]()
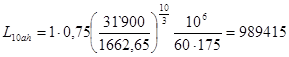 (ч).
(ч).
![]() 7227, ресурс подшипника больше необходимого.
7227, ресурс подшипника больше необходимого.
Быстроходный вал
Расчет на статическую грузоподъемность
Шариковые радиальные однорядные подшипники легкой серии, обозначение 207.
Базовая статическая радиальная грузоподъемность ![]()
![]()
![]()
![]() ,
, ![]() .
.
Расчет на заданный ресурс.
Исходные данные:
![]() =0; d=35
=0; d=35 ![]() ;
; ![]() ;
;![]() ;
;![]() ;
;
![]()
![]() ;
; ![]() .
.
![]() , X=1, Y=0.
, X=1, Y=0.
Эквивалентная динамическая нагрузка:
V=1; ![]() ;
;![]() ;
;
![]()
![]() ;
;
Эквивалентная радиальная динамическая нагрузка:
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
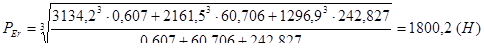
Определение расчетного ресурса подшипника:
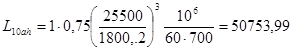 (ч).
(ч).
![]() 7227, ресурс подшипника больше необходимого.
7227, ресурс подшипника больше необходимого.
2.5 Расчет шпоночных соединений
Шпонки проверяют на смятие.
![]() .
.
где ![]() - напряжение смятия, действующее на шпонку, Па;
- напряжение смятия, действующее на шпонку, Па;
![]() - допускаемое напряжение смятия, МПа;
- допускаемое напряжение смятия, МПа;
Для неподвижных соединений допускают:
при переходной посадке и стальной ступице ![]() ;
;
при посадке с натягом и стальной ступице ![]() ; (см.[7], с.90)
; (см.[7], с.90)
![]() - площадь смятия,
- площадь смятия, ![]() ;
;
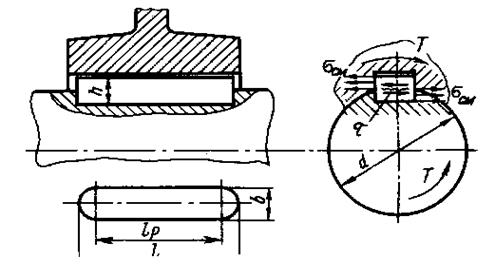
Рисунок 6
![]() ,
, ![]()
где Т – крутящий момент на валу, Нм;
d – диаметр ступицы, м;
![]() - рабочая длина шпонки, м;
- рабочая длина шпонки, м;
![]() - высота выступающей части шпонки, м.
- высота выступающей части шпонки, м.
Промежуточный вал.
Т=65,977 Нм; d=0,038 м; ![]() =0,022 м;
=0,022 м; ![]() =0,003 м,
=0,003 м, ![]() .
.
![]() .
.
Тихоходный вал.
Проверяем шпонку на участке вала диаметром d=0,045 (м).
Т=403,245 Нм; ![]() =0,056 м;
=0,056 м; ![]() =0,0035 м.
=0,0035 м.
![]() .
.
Проверяем шпонку на участке вала диаметром d=0,064 (м).
Т=403,245 Нм; ![]() =0,049 м;
=0,049 м; ![]() =0,0035 м.
=0,0035 м.
![]() .
.
Быстроходный вал.
Т=34,694 Нм; ![]() =0,039 м;
=0,039 м; ![]() =0,0025 м,
=0,0025 м, ![]() м.
м.
![]()
Шпонки подходят.
3. Эскизное проектирование
При эскизном проектировании определяют расположение деталей передач, расстояния между ними, ориентировочные диаметры ступеней валов, выбирают типы подшипников и схемы их установки.
3.1 Проектные расчёты валов
Определение предварительных значений диаметров различных участков валов.
Быстроходный вал:
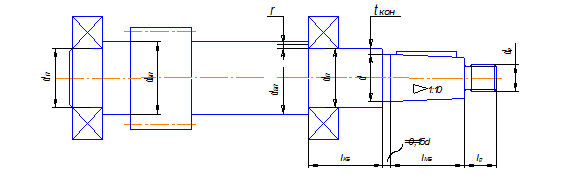
Рисунок 7
![]()
где ТБ – номинальный момент на быстроходном валу,![]() ;
;
![]() - высота заплечника, мм (выбираем в зависимости от диаметра d);
- высота заплечника, мм (выбираем в зависимости от диаметра d);
![]() - координата фаски подшипника, мм (выбираем в зависимости от диаметра d).
- координата фаски подшипника, мм (выбираем в зависимости от диаметра d).
![]()
Вследствие необходимости согласования с валом электродвигателя принимаем d=32 мм,
![]()
![]() ,
,
принимаем ![]() (до ближайшего посадочного диаметра подшипника).
(до ближайшего посадочного диаметра подшипника).
![]() ,
,
принимаем ![]() (округляем до ближайшего значения из стандартного ряда).
(округляем до ближайшего значения из стандартного ряда).
Промежуточный вал:
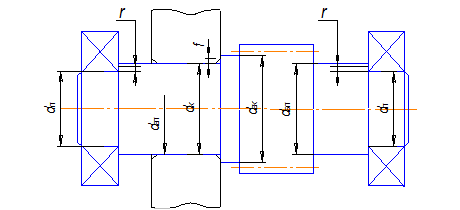
Рисунок 8
![]()
![]()
где ![]() - номинальный момент на промежуточном валу,
- номинальный момент на промежуточном валу,![]() ;
;
![]() - размер фаски колеса, мм (выбираем в зависимости от диаметра d).
- размер фаски колеса, мм (выбираем в зависимости от диаметра d).
![]() принимаем
принимаем ![]() ,
, ![]() =1,2 мм,
=1,2 мм, ![]()
![]() так как фаска ступицы равна 1,6 мм, то принимаем
так как фаска ступицы равна 1,6 мм, то принимаем ![]()
![]() , принимаем
, принимаем ![]() .
.
![]()
Тихоходный вал:
Рисунок 9
![]() .
.
где ![]() - номинальный момент на тихоходном валу,
- номинальный момент на тихоходном валу,![]() .
.
![]() принимаем
принимаем ![]() ,
, ![]() ,
, ![]() .
.
![]() принимаем
принимаем ![]() .
.
![]()
![]()
3.2 Определение расстояние между деталями передач
Чтобы поверхности вращающихся колес не задевали за внутренние поверхности стенок корпуса, между ними оставляют зазор «![]() » (мм):
» (мм):
![]()
где L – расстояние между внешними поверхностями деталей передач, мм.
![]()
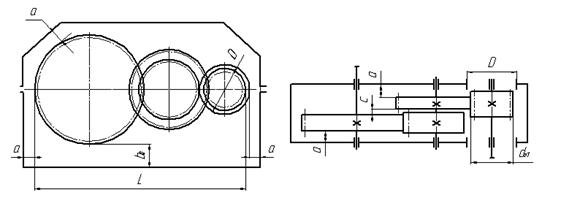
Рисунок 10
Расстояние между торцовыми поверхностями колес двухступенчатого редуктора, выполненного по развернутой схеме, принимают ![]() .
.
![]() .
.
3.3 Выбор типа и схемы установки подшипников
Для опор валов цилиндрических прямозубых и косозубых колес редукторов применяют чаще всего шариковые радиальные подшипники. Первоначально назначают подшипники легкой серии. Для опор плавающих валов шевронных передач принимают радиальные подшипники с короткими цилиндрическими роликами, первоначально также легкой серии. Обычно используют подшипники класса точности 0. Применение подшипников более высоких классов точности повышает стоимость изделия.
Выбираем:
для тихоходного вала – подшипники 211;
для промежуточного вала – подшипники 2207;
для быстроходного вала – подшипники 207.
В большинстве случаев валы должны быть зафиксированы в опорах от осевых перемещений. По способности фиксировать осевое положение вала опоры разделяют на фиксирующие и плавающие. Используя рекомендации выбираем для тихоходного и быстроходного валов схему фиксации «враспор». Промежуточный вал делаем плавающим.
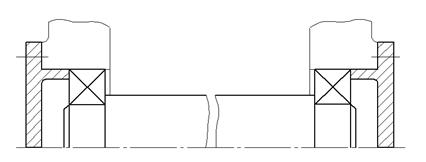
Рисунок 11
Определение толщины стенки корпуса.
Для редукторов толщину стенки, отвечающую требованиям технологии литья, необходимой прочности и жесткости корпуса, вычисляют по формуле:
![]()
где Т – вращающий момент на тихоходном валу,![]() .
.
![]() , принимаем =8 мм.
, принимаем =8 мм.
Определение диаметра болтов для крепления крышки к корпусу редуктора.
Диаметр d (мм) винтов крепления крышки принимают в зависимости от вращающего момента Т
(![]() ) на выходном валу редуктора:
) на выходном валу редуктора:
![]()
![]() , принимаем d = 12 мм.
, принимаем d = 12 мм.
Определение диаметра штифтов.
При сборке редуктора нужно точно фиксировать положение крышки относительно корпуса. Необходимую точность фиксирования достигают штифтами, которые располагают на возможно большем расстоянии друг от друга. Диаметр штифтов:
![]() , ([5], с. 266)
, ([5], с. 266)
где d – диаметр крепежного винта.
![]() , принимаем
, принимаем ![]() .
.
Определение диаметра болтов для крепежа редуктора к фундаменту.
Диаметр болтов для крепежа редуктора к фундаменту
![]() , ([5], с.267)
, ([5], с.267)
где d – диаметр крепежного винта.
![]() , принимаем
, принимаем ![]() .
.
Диаметр отверстия под болт крепления к плите: ![]() . Диаметр цековки под головку болта:
. Диаметр цековки под головку болта: ![]() Глубина цековки t = 1 (мм).
Глубина цековки t = 1 (мм).
4. Выбор посадок
Посадки подшипников ([5], с. 113).
Различают три типа нагружения колец подшипников: циркуляционное, местное и колебательное нагружения. В зависимости от вида нагружения, типа подшипника и режима работы выбирают посадку подшипника.
| Тип подшипника |
Режим работы |
Кольцо |
Тип нагружения |
Поле допуска вала и отверстия при установке подшипника |
|
| Быстроходный вал |
Шариковый |
|
Внутр. |
Циркуляционное |
k6 |
| Внеш. |
Местное |
Н7 |
|||
| Промежуточный вал |
Роликовый |
|
Внутр. |
Циркуляционное |
k6 |
| Внеш. |
Местное |
Н7 |
|||
| Тихоходный вал |
Шариковый |
|
Внутр. |
Циркуляционное |
k6 |
| Внеш. |
Местное |
Н7 |
Посадки зубчатых колес ([5], с. 78).
По рекомендациям для колес, момент которым передается шпоночным соединением, принимаем:
для колеса поз.9 – Н7/p6;
для колёс поз. 10, 11 – Н7/r6.
Для облегчения сборки предусматриваем направляющие цилиндрические участки валов с полем допуска d11 в местах установки колёс с натягом. Посадки колец выбираем по рекомендациям. (см.[5], с.163)
5. Выполнение рабочих чертежей деталей
При обработке деталей возникают погрешности не только линейных размеров, но и геометрической формы, а также погрешности в относительном расположении осей, поверхностей и конструктивных элементов деталей. Это может вызывать вибрации, динамические нагрузки, шум.
Рабочий чертёж вала-шестерни (поз.4)
На чертеже вала задают необходимые требования точности изготовления отдельных его элементов.
1) Допуск цилиндричности посадочных поверхностей для подшипников качения задают, чтобы ограничить отклонения геометрической формы дорожек качения колец подшипников. Допуск цилиндричности посадочных поверхностей валов в местах установки на них с натягом зубчатых колес задают, чтобы ограничить концентрацию давлений.![]()
![]() 0,5t, где t – допуск на размер.
0,5t, где t – допуск на размер.
2) Допуск соосности посадочных поверхностей для подшипников качения относительно их общей оси задают, чтобы ограничить перекос колец подшипников качения.
![]() принимают по таблице, в зависимости от типа подшипника.
принимают по таблице, в зависимости от типа подшипника.
3) Допуск соосности посадочной поверхности для зубчатого колеса задают, чтобы обеспечить нормы кинематической точности и нормы контакта зубчатой передачи.
![]() принимают по таблице в зависимости от диаметра.
принимают по таблице в зависимости от диаметра.
4) Допуск перпендикулярности базового торца вала назначают, чтобы уменьшить перекос колец подшипников и искажение геометрической формы дорожки качения внутреннего кольца подшипника. ![]() принимают в зависимости от диаметра и типа подшипника.
принимают в зависимости от диаметра и типа подшипника.
5) Допуск перпендикулярности базового торца вала для зубчатого колеса не назначаем, т.к. не выполняется условие ![]() .
.
l=28,5 (мм); d=38 (мм); ![]()
6) Допуски симметричности и параллельности шпоночного паза задают для обеспечения возможности сборки вала с устанавливаемой на нем деталью и равномерного контакта поверхностей шпонки и вала. ![]()
![]() 0,5tшп,
0,5tшп, ![]()
![]() 2tшп, где tшп - допуск ширины шпоночного паза.
2tшп, где tшп - допуск ширины шпоночного паза.
Допуск шпоночного паза призматической шпонки - Р9.
Рабочий чертёж зубчатого колеса (поз. 10)
Допуск цилиндричности посадочной поверхности назначают, чтобы ограничить концентрацию контактных давлений.
![]()
![]() 0,5t, где t – допуск размера поверхности.
0,5t, где t – допуск размера поверхности.
Допуск перпендикулярности торца ступицы задают, чтобы создать точную базу для подшипника качения уменьшить перекос колец подшипников и искажение геометрической формы дорожки качения внутреннего кольца. ![]() на диаметре
на диаметре ![]() при
при ![]() выбираем по таблице. Степень точности допуска при базировании роликовых подшипников – 7.
выбираем по таблице. Степень точности допуска при базировании роликовых подшипников – 7.
На глубину шпоночного паза задают предельные отклонения в зависимости от сечения шпонки.
От 66 до 3218: +0,2 мм.
На ширину шпоночного паза отверстия для призматической шпонки при неподвижном соединении нереверсивной передачи задается поле допуска Js9.
Рабочий чертёж крышки (поз. 21)
Допуск параллельности торцов задают, если по торцу крышки базируют подшипник качения.
Допуск назначают, чтобы ограничить перекос колец подшипников.
По рекомендациям выбираем посадки размера В и диаметра D. (см. [5], с.150)
Для всех деталей по рекомендациям выбираем шероховатости поверхностей в зависимости от их назначения. (см. [5], с.348)
6. Выбор смазки
Для смазывания передач широко применяют картерную смазку. Преимущественное применение имеют масла. Причем чем выше окружная скорость колеса, тем меньше должна быть вязкость масла и чем выше контактные давления в зацеплении, тем большей вязкостью должно обладать масло. Поэтому требуемую вязкость масла определяют в зависимости от контактного напряжения и окружной скорости колес. По таблице выбираем масло марки И-Г-А-32 с кинематической вязкостью 29…35 ![]() .
.
Допустимые уровни погружения колес цилиндрического редуктора в масляную ванну вычисляем по формуле:
![]() ,
,
где m – модуль зацепления, m=2,5 (мм);
![]() - делительный диаметр тихоходного колеса,
- делительный диаметр тихоходного колеса, ![]() =234,5 мм.
=234,5 мм.
Погружаем в масло колеса обеих ступеней.
![]() , принимаем
, принимаем ![]() .
.
![]() ,
,
принимаем
Рисунок 12
Заключение
В целом, данный редуктор представляет собой неплохую конструкцию, имеющую достаточный запас прочности, высокую жёсткость корпуса и удовлетворяющую современным требованиям технической эстетики.
Но возможно внесение некоторых изменений:
1. крышку люка можно заменить составной крышкой – отдушиной;
2. пробку для маслосливного отверстия с цилиндрической резьбой можно заменить на пробку с конической резьбой;
3. если редуктор будет расположен достаточно высоко над уровнем пола, то жезловый маслоуказатель можно заменить на круглый;
Литература
1. Анурьев В.И. Справочник конструктора- машиностроителя. В 3-х т. Т.1.- 5-е изд., перераб. и доп.- М.: Машиностроение, 1978.-728 с., ил.
2. Анурьев В.И. Справочник конструктора- машиностроителя. В 3-х т. Т.2.- 5-е изд., перераб. и доп.- М.: Машиностроение, 1980.- 559 с., ил.
3. Анурьев В.И. Справочник конструктора- машиностроителя. В 3-х т. Т.3.- 5-е изд., перераб. и доп.- М.: Машиностроение, 1980.- 557 с., ил.
4. Добровольский В.П. Расчёт цилиндрических зубчатых передач внешнего зацепления: Методические указания.- Омск, 1994.- 22 с., ил.
5. Дунаев П.Ф., Леликов О. П. Конструирование узлов и деталей машин: Учебное пособие для техн. спец. Вузов.- 7-е изд., испр.- М.: Высш. шк., 2001.- 447 с.: ил.
6. Дунаев П. Ф., Леликов О. П., Варламова Л. П. Допуски и посадки. Обоснование выбора: Учебное пособие для студентов машиностроительных вузов.- М.: Высш. шк., 1984.-112 с., ил.
7. Иванов М.Н. Детали машин: Учеб. для студентов втузов/Под ред. В.А. Финогенова. – 6-е изд., перераб. – М.: Высш. шк., 2000.- 383 с.: ил.
8. Мехаев М.Б. Предварительный расчёт привода: Методические указания к курсовому проекту по деталям машин.- Омск, 1999.- 32 с., ил.
9. Феодосьев В.И. Сопротивление материалов: Учебник для втузов – 9-е изд., перераб. – М.: Наука. Гл. ред. физ.-мат. лит. 1986. – 512 с.