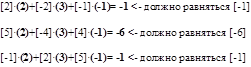Решение матриц
СОДЕРЖАНИЕ: Правила произведения матрицы и вектора, нахождения обратной матрицы и ее определителя. Элементарные преобразования матрицы: умножение на число, прибавление, перестановка и удаление строк, транспонирование. Решение системы уравнений методом Гаусса.Умножение
Умножение матриц (Произведение матриц):
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы .
Это условие не выполняется, произведение АВ не существует.
Произведение матрицы и вектора А b :
![]()
Скалярное произведение векторов ( b ,с):
![]()
Найти определитель матрицы А:
В частности, формула вычисления определителя матрицы ![]() такова:
такова:
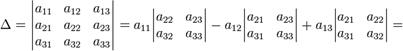
= a 11 a 22 a 33 a 11 a 23 a 32 a 12 a 21 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 a 13 a 22 a 31
=2*(-4)*5 – 2*4*2 – (-2)*5*5 + (-2)*4*(-1) +(-1)*5*2 – (-1)*(-4)*(-1) = -40 – 16 +50 + 8 – 10 + 4 = -4
Найти обратную матрицу А-1 :
Решение .
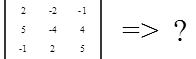
Определитель введенной Вами матрицы равен:
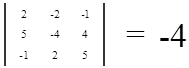
Определитель не равен нулю, следовательно обратная матрица существует.
Допишем к исходной матрице единичную матрицу справа.
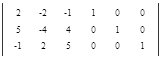
Начнем приведение левой квадратной матрицы к единичному виду. При помощи элементарных преобразований уберем все коэффициенты ниже главной диагонали.
Вычтем 1 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
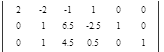
Вычтем 2 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
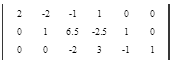
Приведем все коэффициенты на главной диагонали матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки находящийся на главной диагонали, если он не равен 1.
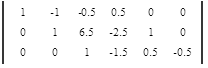
Приведем все коэффициенты выше главной диагонали к 0, при помощи элементарных преобразований.
Вычтем 3 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
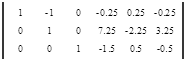
Вычтем 2 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
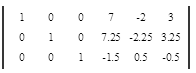
Ответ .
Как уже ранее упоминалось, мы при помощи элементарных преобразований переместили единичную матрицу из правой части в левую, при этом не нарушив ни одного правила работы с матрица.
Квадратная матрица, которую Вы видите справа и есть обратная матрица к введенной Вами .
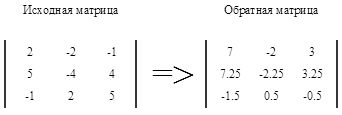
Решение системы уравнений Ах= b :
Условие
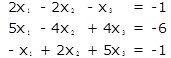
Решение
Найдем определитель главной матрицы, составленной из коэффициентов при X1 - n :
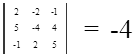
Определитель главной матрицы системы уравнений не равен нулю, следовательно данная система уравнений имеет единственное решение. Найдем его. Достоим главный определитель системы уравнений еще одним столбцом, в который вставим значения за знаком равенства.
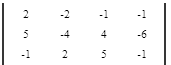
Теперь последовательно, при помощи элементарных преобразований преобразуем левую часть матрицы (3 3) до треугольного вида (обнулим все коэффициенты находящиеся не на главной диагонали, а коэффициенты на главной диагонали преобразуем до единиц).
Вычтем 1 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
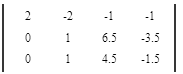
Вычтем 2 - ую строку из всех строк, которые находятся ниже нее. Это действие не противоречит элементарным преобразованиям матрицы.
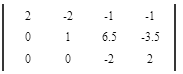
Вычтем 3 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
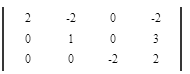
Вычтем 2 - ую строку из всех строк, которые находятся выше нее. Это действие не противоречит элементарным преобразованиям матрицы.
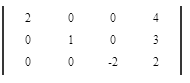
Приведем все коэффициенты на главной диагонали матрицы к 1. Поделим каждую строку матрицы на коэффициент этой строки находящийся на главной диагонали, если он не равен 1.
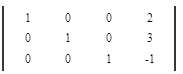
Ответ .
Числа получившиеся правее единичной матрицы и будут решением Вашей системы уравнений.
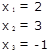
Элементарные преобразования матрицы
Элементарными преобразованиями матрицы называются следующие преобразования: 1) умножение строки матрицы на число, отличное от нуля; 2) прибавление к одной строке матрицы другой строки; 3) перестановка строк; 4) вычеркивание (удаление) одной из одинаковых строк (столбцов); 5) транспонирование матрицы ;
Те же операции, применяемые для столбцов матрицы , также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу матрицы прибавить линейную комбинацию остальных строк (столбцов).
Начинаем решать вот такую систему уравнений методом Гаусса

Определитель основной матрицы равен -4
Хотим сделать элемент [1,1] равным 1. Разделили всю строку 1 на элемент [1,1]=2.
![]()
Сделали в 1 строке элемент 1 единичным.
Обнулим 1 столбец: Из 2 строки вычли 1 строку , умноженную на элемент [1,2]=5.
![]()
Из 3 строки вычли 1 строку , умноженную на элемент [1,3]=-1.
![]()
Преобразование 1 столбца сделали.
Хотим сделать элемент [2,2] равным 1. Разделили всю строку 2 на элемент [2,2]=1.
![]()
Сделали в 2 строке элемент 2 единичным.
Обнулим 2 столбец: Из 1 строки вычли 2 строку , умноженную на элемент [2,1]=-1.
![]()
Из 3 строки вычли 2 строку , умноженную на элемент [2,3]=1.

Преобразование 2 столбца сделали.
Хотим сделать элемент [3,3] равным 1. Разделили всю строку 3 на элемент [3,3]=-2.

Сделали в 3 строке элемент 3 единичным.
Из 1 строки вычли 3 строку , умноженную на элемент [3,1]=6.

Из 2 строки вычли 3 строку , умноженную на элемент [3,2]=6.5.

Преобразование 3 столбца сделали.
Ну вот вроде и все. Решение содержится в правом столбце: ![]() Быстренько сделаем проверку: Исходная матрица:
Быстренько сделаем проверку: Исходная матрица:
![]()
Подставим в исходную матрицу полученные решения: в квадратных скобках элементы матрицы, в круглых решения системы уравнений